高中数学教学中培养数学思维能力的策略初探

梁木华

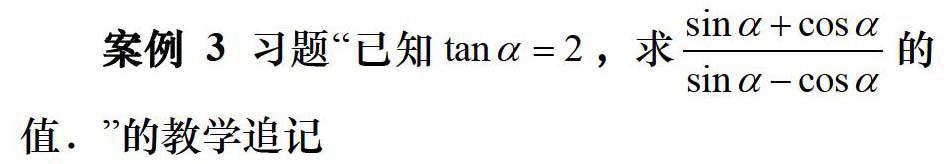
在求学生涯中，高中教育至关重要，它是学生未来发展的基础环节。而且高中学生正处于全面快速发展时期，高中教师在教学过程中，不仅要帮助学生掌握理论知识，还要培养学生形成良好的数学思维能力，只有这样，才能提高学生的创新能力以及学研能力，不断开拓学生思维，为学生的深层次发展奠定思维基础。

1数学思维能力培养的重要意义

1.1符合素质教育的需求

随着我国综合国力的不断发展，社会知识化建设日益深化，高中数学的传统教学模式的滞后性逐渐显露，对学生的长期发展存在较大的制约性，因此，高中应积极响应课标课程改革所提倡的素质教育理念。

数学是高中学段的重点课程，基于素质教育理念的引领，在教学过程中，教师应以培养学生数学思维能力为教学的根本目标。传统教学模式下，教师往往采取题海战术，导致学生思维定式，难以对数学知识变通应用，数学成绩并不理想，而通过素质教育，培养学生形成数学思维发展模式，能提高学生对各类数学题型的应对能力，促使学生能灵活应用数学知识，提高学生数学成绩。

1.2符合社会发展的需求

《普通高中数学课程标准（实验）》明确提出：“高中数学课程的总目标是：使学生在九年义务教育数学课程的基础上，进一步提高作为未来公民所必要的数学素养，以满足个人发展与社会进步的需要”。这意味着，高中阶段的数学教学承负着培养学生数学素养的重任。

由于数学思维能力是数学素养不可或缺的组成因子，因而数学思维能力的培养应该是高中数学教育的重要关注。这既是课标课程的要求，更是社会发展的要求。

人类实际生活中处处均存在数学知识，培养学生数学思维能力，不仅可以提高学生数学解题的效率，还能为学生的现实生活提供较大的助力。同时，培养学生的数学思维能力，有利于帮助学生摆脱思维定式的束缚，促使学生形成发散思维以及逆向思维，为学生日后生活与工作提供便利条件，促使学生的个人价值全面发挥，为社会创造更为显著的经济效益。

2培养数学思维能力的策略

2.1打破传统定式思维

要在高中教学中帮助想培养学生形成良好的数学思维能力，应通过合理有效的渠道，对学生的思维特点进行深入且全面的了解，准确把握学生思维的不足之处。

教学实践中，广大教师默默无闻在做的且行之有效的方法莫过于数学测试、分析学生错误解题以及沟通交流等，如此既奠基于理性层面又激发于感性层面了解学生的思维能力，然后在实际教学过程中，采取针对性措施，引导学生发散思维，帮助学生破除传统定式思维，提高学生的数学思维能力。

本例不仅仅是多数学生无法正确求解，教师在教学中也容易因为思维定式而导致解答不完整。

课标课程倡导的课程理念明确告诉我们，数学教学不仅仅是知识的教学，更应该把学生发展的着眼点放在提高思维能力的层面上，传统的双基训练、变式练习仍然不失为一种有效的方法。然而像如上稍加类比、拓展即可得到一个有用工具的做法应该说是有必要的，教师们一定要活用教材，真正把精力放在提高学生的思维能力上，使“定式”不“定”。

2.2生活化数学知识

相对高中学段的其他课程而言，数学知识的应用领域十分宽广，它与人类实际生活之间存在非常密切的关联，数学知识源于实际生活，也归于实际生活。因此，教师在实际教学过程中，可以有效连接实际生活与数学知识，借助生活实例，阐述数学知识，这样不仅可以促使抽象化数学知识实现具象化，加深学生对数学知识的理解程度，还能激发学生的学习兴趣，活跃学生的学习思维，为学生形成良好的数学思维能力创造良好的培育环境。

案例2培养数学思维能力的一个教学片断

为了帮助学生形成良好的数学思维能力，笔者在讲解正三角形知识时，让学生以同桌为单位，用六根笔拼成四个全等正三角形。

受定势思维的影响，学生在同一平面内进行拼凑，发现无论如何也完不成任务。笔者适时予以引导：“数学都是研究同一平面内的对象吗？当我们站立时，对比地面而言，我们与地面处于相同平面吗？”学生利用空间立体知识，很快便完成了教师布置的任务。

对于学生而言，笔是其接触最多的用品之一，无论是学习、工作，还是生活，人们均需要用笔。教学实践中，诸如此类用六支笔拼成四个全等正三角形的任务，在实际教学中还不胜枚举，这样的教学设计打破了学生的定式思维，锻炼了其空间想象力，在很大程度上提高了学生数学题的解答能力。

“从最简单的情形开始”是笛卡尔的名言，著名数学家华罗庚也说过善于‘退，足够地‘退，退到最原始而不失去重要性的地方，是学好数学的诀窍。”其实，优质、高效的数学课堂教学何尝不是这样的。

2.3拓展学生的解题思路

在高中数学教学过程中，对解题方法以及思路进行分析探究十分必要。应该明确，让学生发现或得到正确答案并不是最主要的，更主要的应该是让学生在解题过程中，明晰解题思路，合理展开思考，并进而形成良好的数学思维能力。

在解题过程中，学生需要对例题进行详细思考，明确例题中都包含哪些有效条件以及最终问题指向。然后对例题进行全面分析，在这种审题过程中，便是培养学生形成数学思维能力的最佳时期。例如，教师在讲解函数单调性知识点时，学生普遍会将单调性证明题与反证法证明题进行对比，因为教材所给的证明步骤不够详细，认为单调性证明题较为简易，这时，教师便应对学生的解题思维进行深入启发，通过对习题内容进行重新组织，让学生在思考的过程中，形成问题解决能力以及思考能力。

面对这道习题时，学生已经具备了一定的三角函数知识基础，对化归思想在求解三角函数问题中的运用也有了一定的体验。因此，笔者在教学中就尝试放手给学生自己处理此类问题。结果是：约有60%的学生用“切化弦”的解法，约40%的学生用“弦化切”的解法。而惭愧的是，同样题目的教学，笔者之前的一次教学实施采用直接讲授灌输解法，而且着重只板演一种“弦化切”的解法，另一种“切化弦”的解法只是一语带过。后来在一次专项测试中，结果出乎意料，全班50人有44人即近90%的学生用教师讲授的“弦化切”的解法。

很多学生在实际解题过程中，会存在直觉性解题方法，这是学生长期灌输式讲授法的弊端，看到类似题目，脑海中便会直接出现解题方式，导致学生不会对例题进行深入探究，不利于学生深入掌握数学知识。教师必须将培养学生数学思维能力作为教学重点，在例题讲解过程中，不断引导学生开拓思维，一题多法多思路解题，促使学生形成良好的发散思维能力以及创新思维能力。

由此可见，教师如果能弃“训化”为“教化”，而是放手给学生自己处理，给予学生更广阔的空间，拓展学生的解题思路。教育感化，为拓展学生的解题思路注入情感基础，而这情感基础又是必不可少的，这里既有知识的完善，又含有人格的健全，还包括情感的体验，数学思维能力培养中情感先行也是势在必行。