浮山县尧山森林公园太和桥结构设计的探讨

罗 强

（山西省交通科学研究院，山西 太原 030006）

1 工程概况

太和桥位于位于山西省临汾市浮山县城东隅尧山森林公园内，是一座两跨矮塔斜拉桥，跨径布置为84.8+84.8=169.6 m。主梁为局部变高的斜腹板单箱单室混凝土箱梁，顶板宽7.5 m，底板宽3.81 m；等高段梁高1.5 m，根部梁高6.0 m，0号块两侧23 m范围内为变高段；顶板厚0.25 m，0号块局部加厚为0.5 m；标准截面底板厚0.22 m，0号块底板加厚为0.9 m，两侧47 m范围内底板厚由0.7 m变化为0.22 m；腹板为斜腹板与直腹板相结合的方式布置，梁高变化通过加高直腹板来实现，腹板厚分别为0.3 m、0.5 m，之间通过12 m进行渐变。

塔、梁、墩三者之间的关系为：塔梁固结、墩梁之间通过支座连接。桥塔采用框架式结构，两肢塔柱之间横向净距4 m，通过横梁相连；塔肢横向宽1.2 m，底部纵向尺寸3.5 m，顶部渐变为5.0 m，塔肢间横梁做复古镂空风格装饰；桥墩为4 m×6 m薄壁空心矩形截面，壁厚0.5 m，侧面做凹槽处理，墩顶截面横桥向壁厚加强为1 m。承台平面为八边形，厚度4 m，桩基采用直径1.5 m，长58 m，共12根。

2 模型建立

参照设计图纸的具体尺寸，利用有限元软件MIDAS CIVIL 2012建立全桥整体计算模型，模型中单元共计233个，节点235个，桥塔和主梁通过梁单元模拟，拉索通过桁架单元模拟，支座通过弹性连接来模拟，墩底按照固结处理，建立的有限元模型如图2。

图2 有限元计算模型

2.1 材料

a）拉索 采用250AT-19型1860钢绞线；

b）桥塔、桥墩 C40混凝土；

c）主梁 C60混凝土；

d）预应力 1860钢绞线。

2.2 荷载

a）自重 将结构质量转换为自重，系数-1.04。

b）挂篮、施工机具人员等 悬臂端两侧各600 kN。

c）施工阶段拉索张拉值 2 500 kN（近塔侧）、2 500 kN、2 500 kN、2 000 kN、1 600 kN（远塔侧）。

d）二期 栏杆，20 kN/m；铺装，70 kN/m。

e）收缩、徐变 单元激活时龄期7 d，相对湿度70%，水泥种类系数5，收缩开始龄期3 d。

f）预应力 张拉应力取0.75ftk，锚具变形、钢筋回缩 6 mm（单端），摩擦系数 μ=0.17，偏差系数0.001 5，松弛系数 0.3。

g）静阵风荷载 按照《公路桥涵设计通规》[1]施加，设计基本风速27.7m/s，施工阶段，风速重现期0.84。

h）人群 3.5 kN/m2，桥面净宽4 m。

i）整体温度 升温30℃，降温40℃。

j）温度梯度 按照《公路桥涵设计通规》施加，其中升温T1=25℃，降温T1=-12.5℃。

k）索梁温差 ±20℃。

l）塔侧温差 塔肢纵向线性温度梯度5°。

m）不均匀沉降 ±10 cm。

n）换索工况 一次只拆掉一组拉索。

2.3 施工过程

结构内力状态和它的施工方法密切相关[2]，要得到结构的内力状态必须模拟其施工过程，该桥主要的施工过程如下：

a）桥墩施工；b）0 号块以及桥塔的施工；c）墩梁临时锁定；d）1号块浇筑，7 d后张拉预应力；e）移动挂篮，浇筑 2号块；f）张拉 2号块预应力；g）重复e～f，至张拉 5 号块预应力；h）张拉 1 号斜拉索；i）重复g～h，至张拉5号斜拉索；j）支架上浇筑边跨现浇段；k）浇筑合拢段；l）张拉合拢束并拆掉挂篮；m）去掉临时锁定，永久支座就位；n）施加二期荷载，铺装及护栏；o）10年收缩徐变。

3 静力计算结果

3.1 拉索

拉索是重要的承载构件，在各状态下索力最大值见表1，可见，拉索在施工中、运营中以及换索状态下，各拉索的索力均在容许范围内。

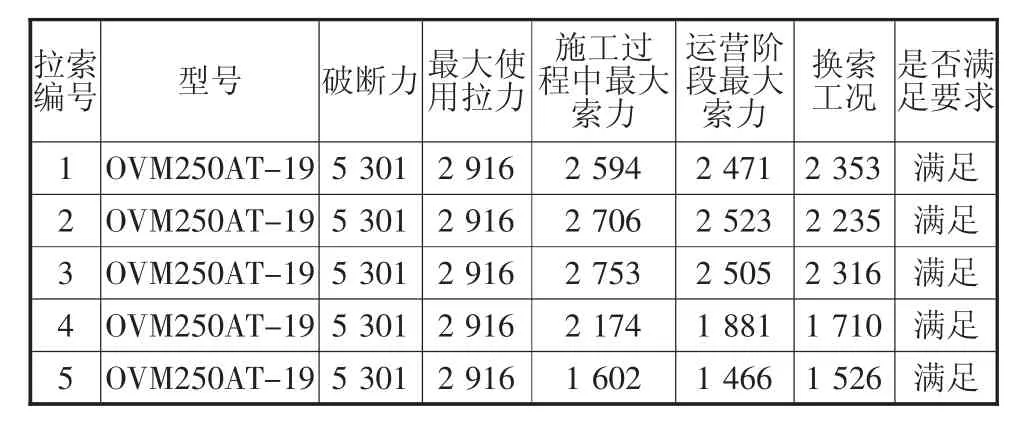
表1 拉索索力表 kN

3.2 主梁

预应力混凝土主梁必须满足《规范》[3]的各项指标要求。主梁各项验算的具体结果见表2，可见主梁的正截面抗裂、斜截面抗裂验算均满足要求，截面法向应力和主压应力均小于规范限制，同时短暂状况的应力大小均满足规范要求。

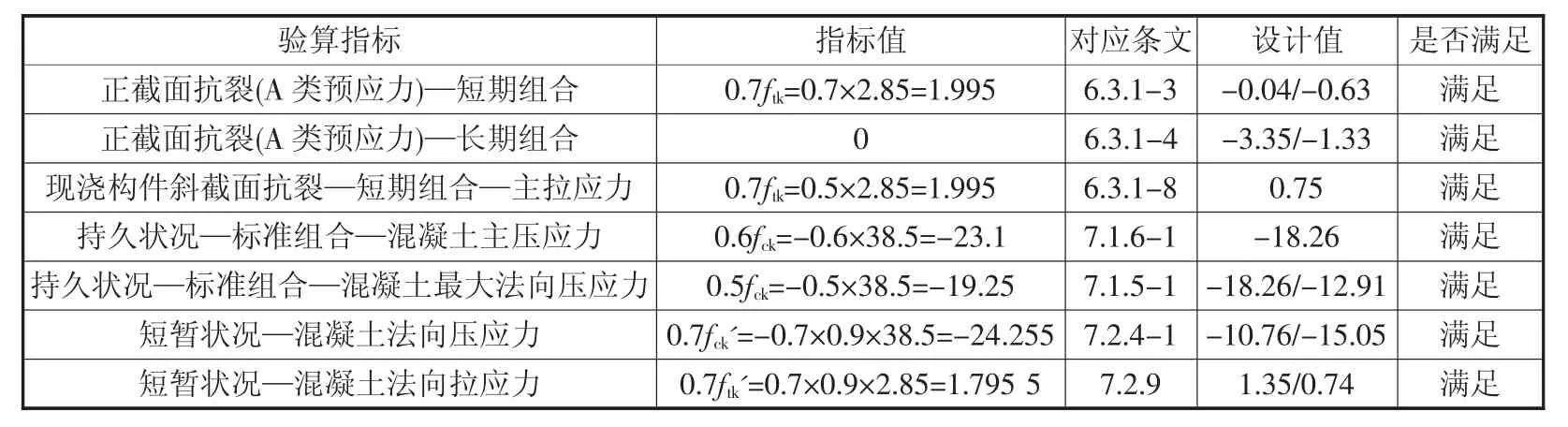
表2 主梁各项验算结果

4 换索验算

按照相关规范[4]的要求，拉索应是可更换的，在拉索的拆除和更换过程中，桥梁将暂时封闭，不容许行人通过，主梁应满足短暂状况的设计要求。表3列出了拉索更换时主梁断面上下缘的法向应力值。可见，在更换拉索的过程中，主梁上下缘均处于受压状态，且最大压应力为10.4 MPa，出现在拆除3号索和4号索时的1/8跨截面下缘，远小于规范要求的限值24.255 MPa，满足短暂状况的设计要求。

对比成桥状态可以看出，在拆除3号拉索时，截面应力变化最大，5/8跨处断面的下缘应力由6.5 MPa降为3.9 MPa，降低了2.4 MPa，但仍处于受压状态。

综合来看，拆除某一对拉索对主梁的应力水平影响并不大，这主要是由于拉索拆除时主梁已处于连续梁状态，与施工过程中的悬臂状态相比，其刚度变大，仅拆除一对拉索对主梁的影响有限。

表3 各换索工况下主梁应力状态 MPa

5 颤振稳定验算

本桥桥宽5.7 m，跨度84 m，宽跨比较小，需验算结构在成桥状态和最大悬臂状态下的颤振稳定性。颤振稳定性验算要用到主梁的第一阶扭转频率，而MIDAS CIVIL 2012建立的梁单元模型无法得到扭转振型，为此需利用板单元模拟主梁来建立新的模型。为验证板单元模型求解振型的有效性，将两种模型得到的前四阶模态进行对比，见图3～图10，可见两个模型前四阶的模态振型完全一致，除第二阶模态频率相差为12%外，其他三阶频率相差均在10%以内，据此可认为利用板单元模型求解结构自振模态是可靠的。

图3 板单元模型第一阶振型(纵漂，0.62 Hz)

图4 梁单元模型第一阶振型(纵漂，0.58 Hz)

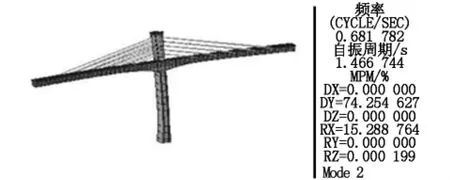
图5 板单元模型第二阶振型(横弯，0.68 Hz)

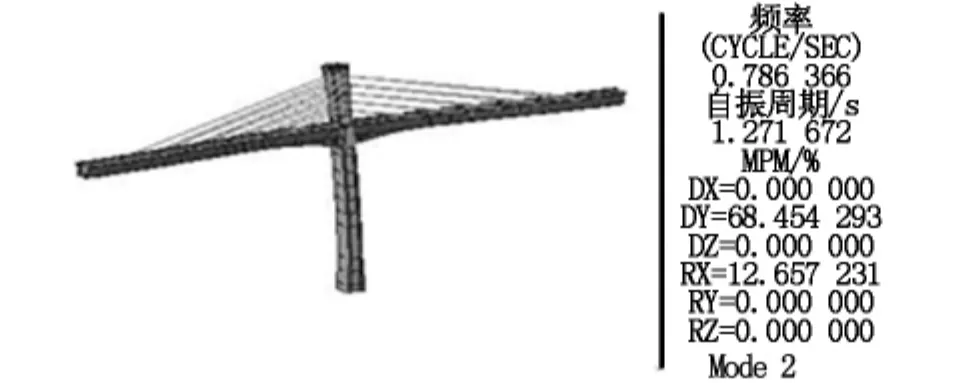
图6 梁单元模型第二阶振型(横弯，0.78 Hz)

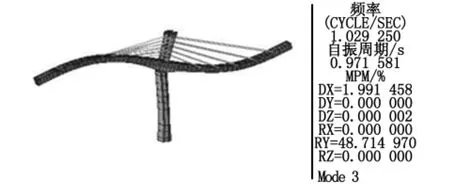
图7 板单元模型第三阶振型(竖弯，1.03 Hz)

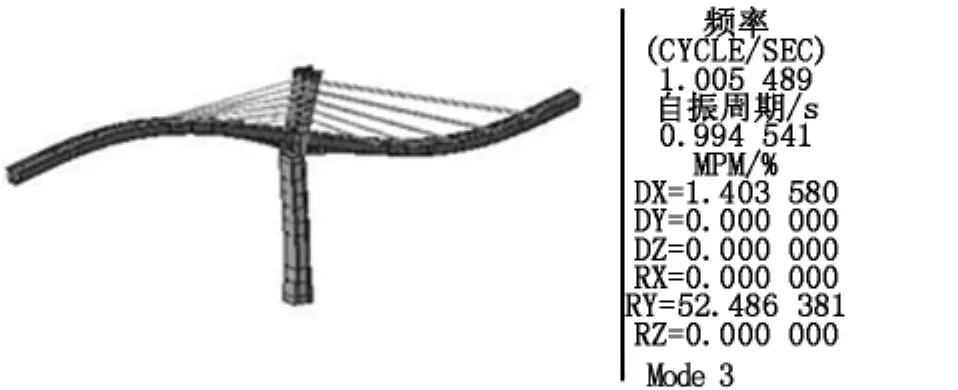
图8 梁单元模型第三阶振型(竖弯，1.01 Hz)

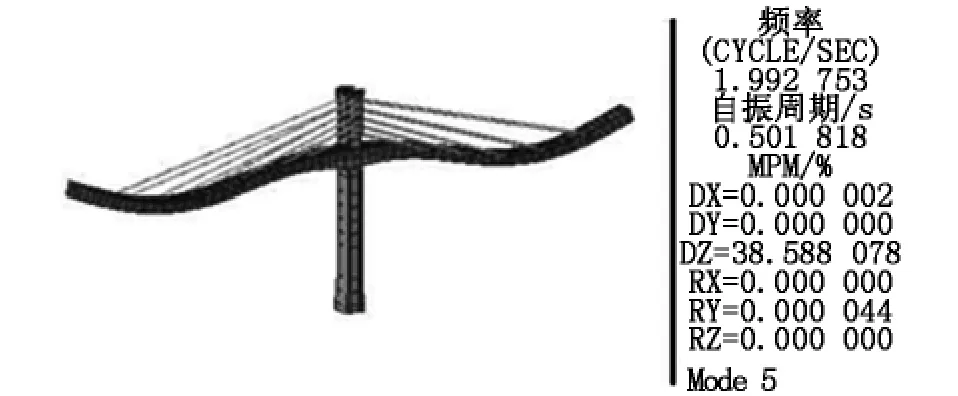
图9 板单元模型第四阶振型(竖弯，1.99 Hz)

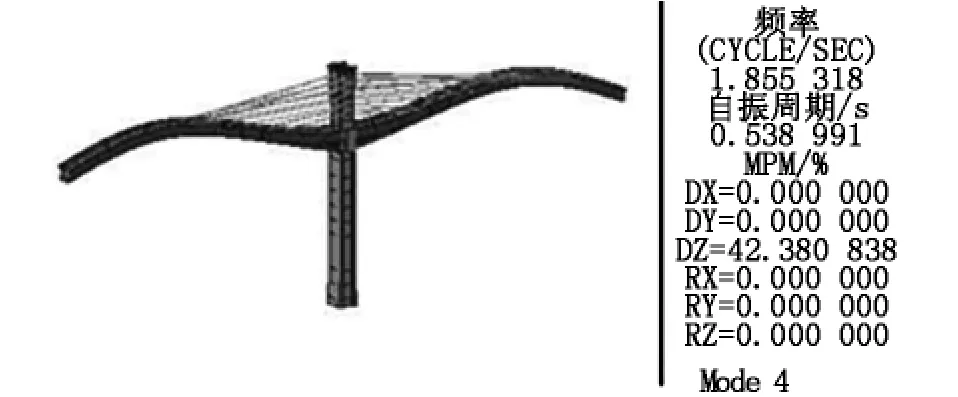
图10 梁单元模型第四阶振型(竖弯，1.85 Hz)

在验证了板单元模型求解结构动力特性可行的情况下，利用板单元模型得到的结构在成桥状态和最大悬臂状态时的扭转模态见图11～图14，有图可见成桥状态结构的第一、二阶扭转频率分别为9.24 Hz、10.09 Hz；而最大悬臂状态结构的第一、二阶扭转频率较小，分别为5.92 Hz、6.22 Hz。最大悬臂状态为较不利状态，这是由于成桥状态下主梁处于连续梁状态，扭转方向的自由度受到桥台支座的约束，也处于超静定状态，扭转刚度大，其扭转振型对应的频率必定较高；而在施工过程中，尤其是最大悬臂状态下，扭转方向的自由度仅受到桥墩的约束，是静定状态，扭转刚度较小，其一阶扭转振型的频率相对较低。颤振验算只需考虑最可能发生的情况，即最大悬臂状态。

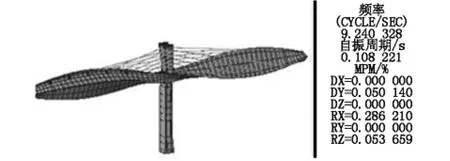
图11 成桥状态一阶扭转振型(9.24 Hz)

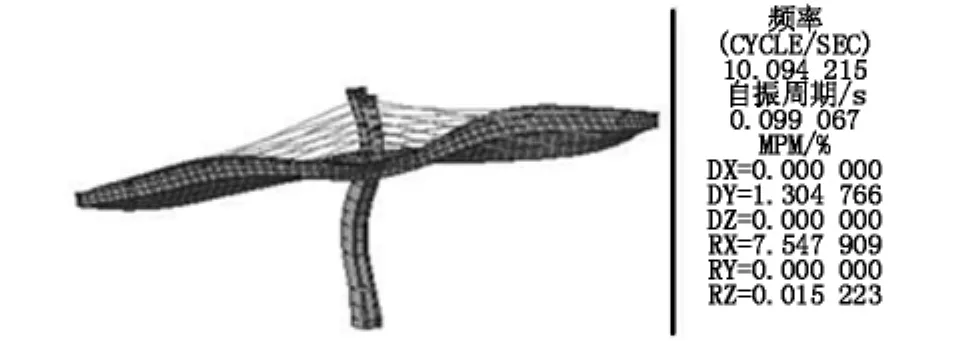
图12 成桥状态二阶扭转振型(10.09 Hz)

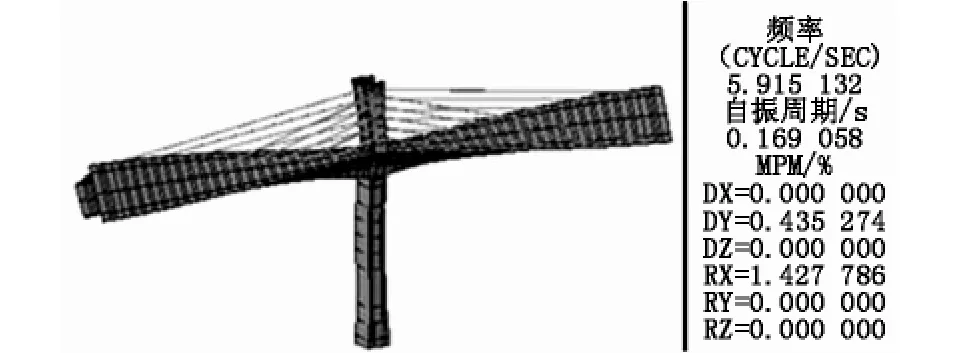
图13 最大悬臂状态一阶扭转振型(5.92 Hz)

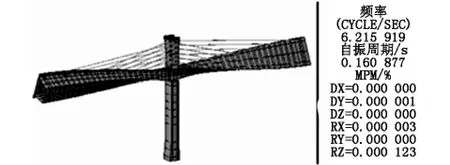
图14 最大悬臂状态二阶扭转振型(6.22 Hz)

得到结构的一阶扭转模态后，根据《公路桥梁抗风设计规范》[5]第6.3节进行颤振稳定分析，验算过程如下。

桥址处地表类别为D类，桥梁跨度84＜100 m，则风速脉动修正系数μf=1.49；设计风速27.7 m/s，颤振检验风速[Vcr]=1.2×μf×Vd=1.2×1.49×27.7=44.18 m/s.

一阶扭转频率5.9 Hz，桥宽5.7 m，颤振稳定指数 If=[Vcr]/ft/B=44.18/5.92/5.7=1.31，If＜2.5，需计算桥梁的颤振临界风速。

b=B/2=5.7/2=2.85 m；空气密度ρ=1.25 kg/m3.

选取主梁跨中截面代表全桥主梁，得到桥面系单位长度质量m=12 000 kg/m，以及桥面系单位长度质量惯矩Im=33 429.5 kg·m2/m.

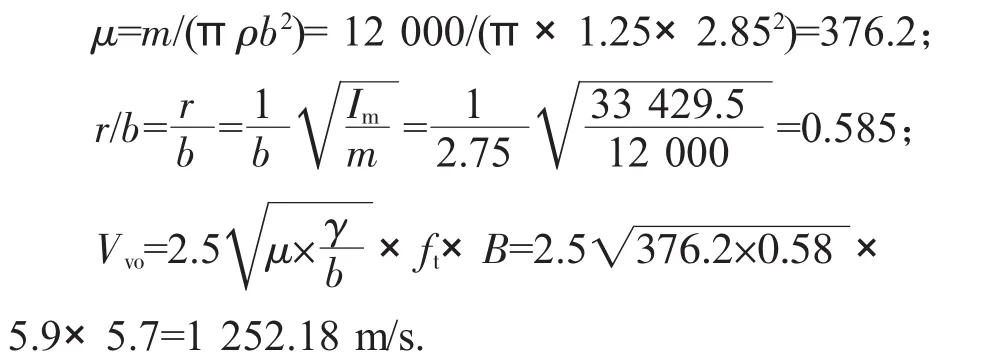
主梁为典型箱型截面，形状系数μs=0.75，攻角系数μα=0.7；颤振临界风速Vcr=μs·μα·Vco=0.75×0.7×1252.18=657.4 m/s.

Vcr≥[Vcr]，满足颤振稳定要求。

6 结论

a）通过一定的拉索和预应力设置，主梁的各项指标均满足A类预应力构件的要求。

b）在换索工况下，主梁全截面均处于受压状态，满足短暂状况下的应力指标。得益于成桥状态下主梁已处于连续梁状态，某一对拉索的拆除，对主梁应力状态影响有限。

c）利用MIDAS CIVIL 2012建立的梁单元模型，不能得到主梁的扭转模态，需借助板单元模型，并通过对比两种模型前几阶模态的情况来验证板单元模型的可靠性。

d）最大悬臂状态而非成桥状态是颤振稳定性最不利的状态，通过验算，该桥的颤振稳定性满足要求。