钢箱梁受压板肋加劲板弹性屈曲性能研究

张亚军

（长平高速公路建设管理处，山西 长治 046100）

加劲肋作为组成钢箱梁上、下翼板的主要构件，既能提升钢箱梁的整体抗弯、扭承载能力，又起到增强上、下翼板局部刚度和受压稳性能的作用[1-4]。

为了分析加劲板的屈曲性能，国内外学者对钢箱梁加劲板在弹性、弹塑性阶段的屈曲性能进行了大量的研究[5-11]，得到了一些有用的结论，并提出了相应的计算理论与设计方法。采用有限元数值模拟方法，系统地分析了板肋刚度与盖板长宽比对加劲肋屈曲性能的影响，同时探讨了经典理论公式的适用范围与内在原因，以期为该类结构的设计与应用提供一定的理论指导和参考依据。

1 板肋加劲板的屈曲特点分析

轴向压力作用下板肋加劲板可能发生下列4种屈曲：a）结构整体屈曲失稳（图1a） 盖板与板肋同时发生屈曲；b）盖板局部失稳（图1b） 板肋刚度过大可能会导致盖板先于板肋发生失稳破坏；c）板肋和盖板均局部屈曲（图1c） 此时板肋和盖板的刚度之比刚好满足盖板与板肋同时局部失稳的条件；d）板肋弯扭失稳（图1d） 板肋高厚比过大或刚度太小时易导致板肋先于盖板失稳。

图1 板肋加劲板的4种屈曲形态

按我国2015版《公路钢结构桥梁设计规范》条文规定设计板肋加劲板算例，基本设计参数：a=b=3.6 m；t=16 mm；w=50 cm；hs=10 cm；ts=10 mm。加劲板的钢材强度等级为Q345qD，弹性模量E=2.06×105MPa，泊松比μ=0.3。加劲板算例构造见图2。

图2 四边简支板肋加劲板

应用通用有限元程序AYSYS 14.0建立板肋加劲板的三维板壳单元模型，盖板与板肋均采用高阶板壳单元shell 181模拟，采用四边简支的边界条件，加劲板纵向承受如图2所示的均布压力。为了进行对比，同时建立与盖板几何尺寸完全相同的无加劲钢板数值模型，进行特征值计算并将结果列于表1中。由表1可知，设置加劲肋能够大幅提高钢板的抗屈曲能力。

图3 无加劲钢板前3阶屈曲模态（纵向）

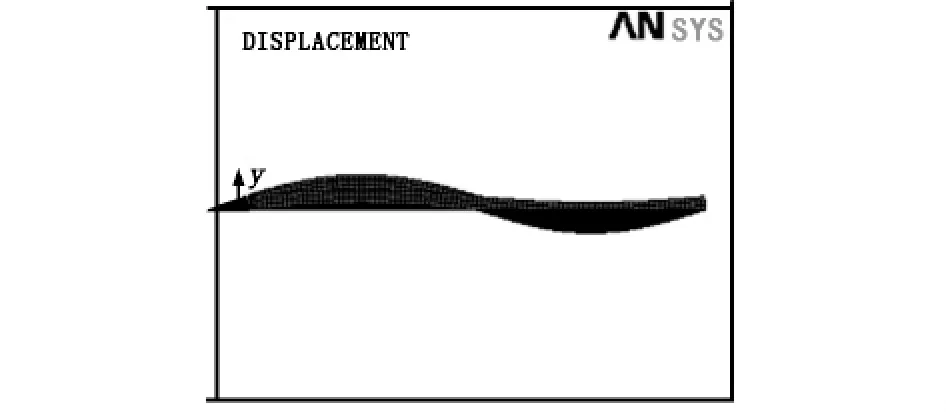
图4 板肋加劲板3阶屈曲模态（纵向）

由图3与图4可知，无加劲钢板1阶模态为纵、横向均半波屈曲；2阶模态为纵向1个整波、横向半波屈曲；3阶模态纵向1.5个正弦波，横向半波屈曲。板肋加劲板1阶模态为纵、横向均半波屈曲；2阶模态为纵向半波、横向一个整波屈曲；3阶模态为纵向一个整波、横向半波屈曲。对比设置板肋前后结构的屈曲模态可以看出，板肋的设置使加劲板在发生与无加劲板相同屈曲模态时需要消耗的能量更大，即失稳荷载越高，设置板肋可改变相同荷载作用下板件的屈曲模态，可提高板件的失稳荷载。

2 板肋刚度对加劲板屈曲性能的影响

以本文板肋加劲板算例尺寸参数为基准，保持板肋高度与厚度之比不变，在0～300 mm范围内变化板肋高度，分别采用有限元数值方法、Timoshenko理论公式、小西一郎理论公式计算加劲板的屈曲临界应力。Timoshenko理论公式与小西一郎理论公式的差别仅在于板肋刚度的计算方法，前者是以盖板下缘为参考轴，而后者的参考轴为盖板中面。计算结果以屈曲临界应力σcr与Q345qD钢材屈服强度σy比值的形式给出，具体数值见表2。

表2 板肋高度变化时四边简支板肋加劲板的σcr/σy

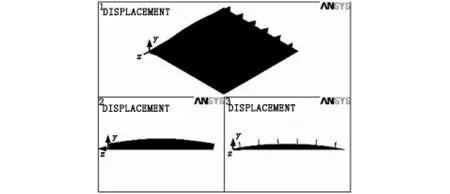
图5 表2中的加劲板屈曲模态①

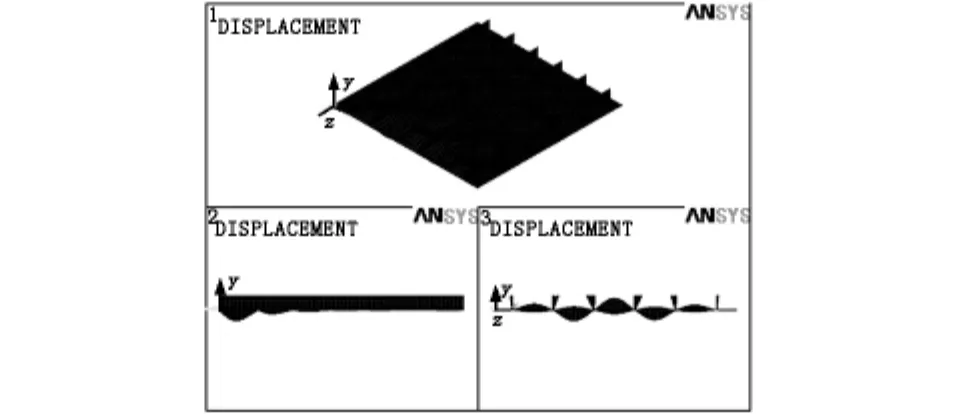
图6 表2中的加劲板屈曲模态②

图7 加劲板屈曲应力与板肋与盖板刚度之比的关系曲线

由表2、图7可知，当板肋与盖板刚度之比（后文简称：刚度比）由0增至39.5（对应的hs=20 cm；ts=20 mm）时，采用3种计算方法得到的1阶临界屈曲应力变化趋势相同，均呈大斜率线性增长，且Timoshenko理论公式与有限元数值解间的最大差值百分比不过0.7%；小西一郎理论公式与有限元数值解间的最大差值百分比为21%；当刚度比大于39.5后，采用3种方法得到的临界应力变化规律不再相同，对于有限元数值解，在刚度比大于39.5后，屈曲应力曲线呈小斜率缓慢增长趋势，即使再成倍增大板肋的刚度，加劲板屈曲应力的提升幅度依然不大；对于Timoshenko与小西一郎理论公式的结果，在刚度比超出39.5后，屈曲应力曲线依然呈大斜率的近似线性增长趋势，当刚度比达到719.82时，有限元数值方法和两种经典理论公式和之间的计算误差高达203.8%。

在此，首先讨论两种理论公式和有限元数值解在刚度比超过39.5后出现如此大的差别的原因。Timoshenko与小西一郎理论公式的表达是相同，即：

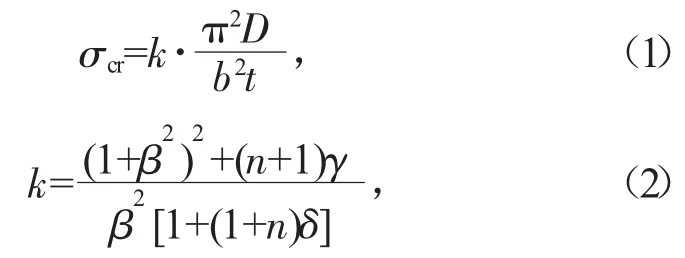
式中：k表示屈曲系数，它是板肋根数n、盖板长宽比β=a/b、板肋与盖板刚度比γ与面积比的相关公式。需特别指出的是，式（2）推导的前提是加劲板在纵横向均发生半波整体屈曲[12]。

根据表2有限元数值结果可知，刚度比由0增至39.5的全过程中加劲板均发生纵横向半波屈曲变形，为柔性板肋加劲板，与理论公式推导假设的屈曲形式一致；当刚度比大于39.5后，加劲板的屈曲破坏形式变化为板肋之间盖板局部屈曲，为刚性板肋加劲板，与理论公式推导假设的屈曲形式不同。究其原因，随着板肋刚度的不断增大，板肋与盖板同时发生整体屈曲所需的能量也不断增大，当刚度比超出临界刚度比后，加劲板整体屈曲消耗的能量比局部屈曲消耗的能量大，此时有限元数值方法计算所得结果为板肋间盖板局部屈曲对应的临界应力，但理论公式的计算结果仍是加劲板纵横向均半波整体屈曲对应的临界应力。

由以上分析结果可知，对于柔性板肋加劲板，增大板肋刚度能有效提高加劲板的屈曲临界应力，而对于刚性肋加劲板，由于结构的屈曲模态为肋间盖板局部屈曲，继续增大板肋刚度对加劲板临界屈曲应力的影响很小，正因为如此，才会出现图7中刚度比大于39.5后有限元数值方法与理论公式计算结果的显著差异。这说明对于设计参数给定的板肋加劲板，板肋的刚度对其屈曲应力的影响较大，合理设计板肋的刚度能有效提高加劲板的屈曲临界应力，但不能无限制地通过增加板肋来提高加劲板的屈曲应力。

3 盖板长宽比对加劲板屈曲的影响

以文中板肋加劲板算例尺寸参数为基准，保持板肋高度与厚度之比不变，在0～250 mm范围内，以50 mm为间隔改变板肋高度hs，同时通过变化盖板长度来控制长宽比β，采用有限元方法分析不同长宽比下，不同板肋高度加劲板在四边简支边界下的屈曲应力，如表3所示。

表3 长宽比、板肋高度同时变化时加劲板的屈曲应力

图8 屈曲应力与盖板长宽比的关系曲线

由表3、图8可知，hs为0、50 mm时，板肋加劲板屈曲应力受长宽比变化的影响较小，屈曲应力曲线基本保持水平；hs为100 mm、长宽比由0.5增至1.5，屈曲应力由221.6 MPa降至41.6 MPa，降幅为81.3%，长宽比对加劲板屈曲应力的影响十分明显，长宽比由1.5增至5.0过程中，屈曲应力仅有小幅上下波动；hs为150 mm、长宽比由0.5增至2.0，加劲板屈曲应力随长宽比的增大而迅速减小，由651.9 MPa降至88.4 MPa，降幅为86.4%，长宽比由2.0增至5.0过程中，屈曲应力曲线基本保持水平；hs为 200 mm、长宽比由 0.5增至 0.75、加劲板的1阶屈曲模态均为加劲板加载端板肋与盖板局部屈曲，屈曲应力基本保持不变，长宽比由0.75增至3.0过程中，屈曲应力随长宽比增大而迅速下降，屈曲应力降幅达82.4%，长宽比继续由3.0增至5.0，屈曲应力曲线基本保持水平；hs为250 mm时，长宽比由0.5增至1.25，加劲板的1阶屈曲模态也是加劲板加载端的板肋与盖板局部屈曲，加劲板屈曲应力基本保持不变，长宽比由1.25增至5.0，屈曲应力随长宽比增大迅速下降，屈曲应力降幅为78.1%。

4 结语

a）分析了板肋加劲板弹性屈曲失稳的特点，依据我国2015版《公路钢结构桥梁设计规范》设计了板肋加劲板稳定算例，分析了板肋对钢板屈曲荷载与屈曲模态的改变程度。

b）分别采用有限元数值方法与理论公式计算了板肋高度变化时板肋加劲板屈曲应力的变化规律，结果表明当板肋与盖板刚度比小于最佳刚度比时，理论公式与有限元法的计算结果吻合；当板肋与盖板刚度比大于最佳刚度比时，由于加劲板实际屈曲破坏形态不同于理论公式推导过程中假设的屈曲破坏形态，两种计算结果间的差异随刚度比的增大而迅速增大。

c）采用有限元数值方法分析了盖板长宽比对板肋加劲板屈曲性能的影响，对于工程常用的板肋加劲板（板肋高度为 10～20 mm），长宽为 0～1.5 时，加劲板屈曲临界应力随长宽比的增大迅速减小；当长宽比为1.5～5.0时，加劲板屈曲临界应力的变化趋于平稳，仅有小幅波动。