换索施工顺序和换索数目对梁塔内力的影响分析

郭 如 炯

(中海(海南)海盛船务股份有限公司，海南 海口 570125)



换索施工顺序和换索数目对梁塔内力的影响分析

郭 如 炯

(中海(海南)海盛船务股份有限公司，海南 海口 570125)

结合某桥梁的工程概况，建立了桥梁平面杆系模型并进行模拟计算，将理论计算和实践测量相结合，分析了换索施工顺序和换索数目的不同对梁塔内力的影响，给出了中小跨径斜拉桥换索的最佳施工顺序和换索数目。

平面杆系，梁塔内力，换索施工，换索数目

对复杂的超静定斜拉桥结构而言，在换索施工控制中存在的不确定影响因素较多，为使换索顺利、安全进行，应对斜拉桥换索施工控制进行详细的分析研究。根据文中所提斜拉桥已有资料，并借助同济大学桥梁博士(V3.0版)进行该桥模型的建立，从换索施工工序、拉索数目不同变化来进行分析、计算，分析不同工序下主梁和索塔的内力影响，给出有利的施工工序，为类似的斜拉桥换索施工控制提供参考[1]。

1 工程概况

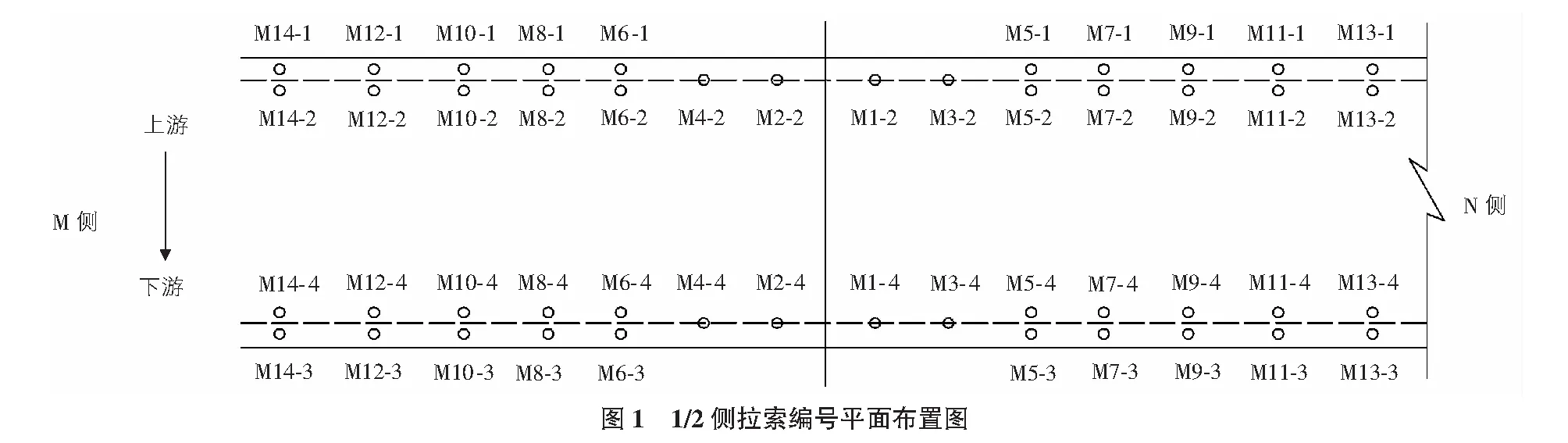
该桥为三跨连续、双塔对称布置的斜拉桥，索塔为双塔双索面、门式框架形式，桥跨形式为70 m+144 m+70 m=284 m，桥面形式为净—(7+2×0.75)m人行道；拉索为扇形布置，且每根主塔对应7对拉索，从上往下的5对斜拉索，由2股拉索组成一组；其余靠下的2对斜拉索是单股形式，故全桥拉索为5×2×8+4×4=96股(为方便索塔上同一位置处的4股拉索交叉固定，两股拉索在边跨左右布置，中跨上下布置)。图1为1/2侧拉索的编号，另外一侧与之对称布置，采用N编号。

2 理论模拟换索施工的研究分析

2.1 换索施工控制计算模型

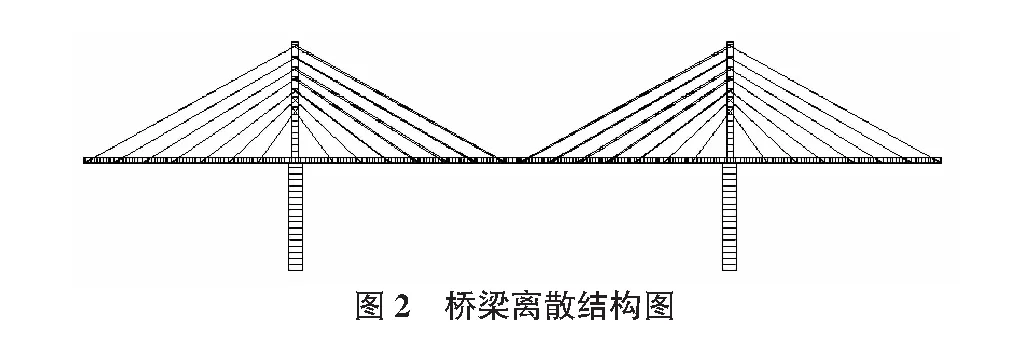
借助同济大学桥梁博士(V3.0版)进行模型的建立、计算和研究分析，该模型的有限元理论依托平面杆系法，看作离散的简化单元组成的集合体，共有468个单元；主塔采用平面梁单元，横向为全截面形式，拉索采用考虑垂度的换算弹性模量的索单元，横隔梁和挂篮均采用集中力方式；边界条件为桥台、墩处主梁竖向位移约束，主塔在承台处固结[2]。模型为一次成桥并输入初始索力的模型，看作初始状态，每个施工阶段对应不同的换索步骤。在施工工序中，拆除某索单元，并将索力值设置为0，即为拆索，模型的受力体系在此过程不发生改变；安装某索单元，并给一索力设计张拉值，即为装新索过程[3]。桥梁离散图如图2所示。

2.2 换索施工顺序对主塔

该桥在实际换索施工中，采用逐塔换索，拆除索数目以2根、4根为宜，上、下游同时进行，依据从外到内、先长索后短索的原理，实践表明上述工序是安全有保证的。为进行对比分析、研究换索工序的不同对主塔内力的影响，以下面2种工序进行建模分析，并对主梁应力进行分析研究[4]。

工序1：模型依据纵桥向从外到内、先长索后短索的顺序进行计算拆除、更换拉索；工序2：模型依据纵桥向从内到外、先短索后长索的顺序进行计算拆除、更换拉索[5]。

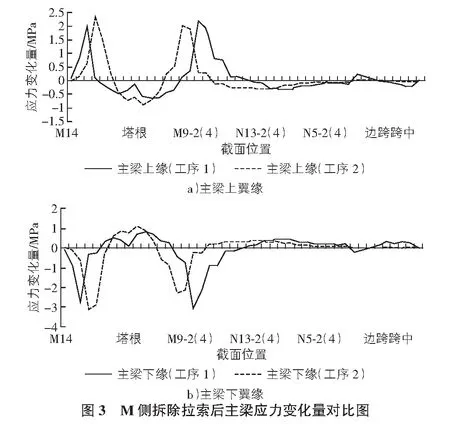
1)主梁应力变化分析。依据上述2种工序下的模型，提取相应数据可知：在更换M侧拉索时，主梁应力变化程度最大，对工序1来说最大施工阶段为更换M10-1，M9-1，M10-3和M9-3号索，对工序2来说为更换N8-2，N7-2，N8-4和N7-4号索，上下翼缘应力在2种工序中改变幅度最大的施工阶段对比图如图3，图4所示。

从图3，图4可以看出，进行拆除、安装拉索位置附近处的主梁截面较其他位置，其应力变化量较大。从图中应力曲线峰值可以看出，工序2模拟计算下的应力峰值较小，对主梁造成的应力变化破坏也小，故适宜采用工序2。

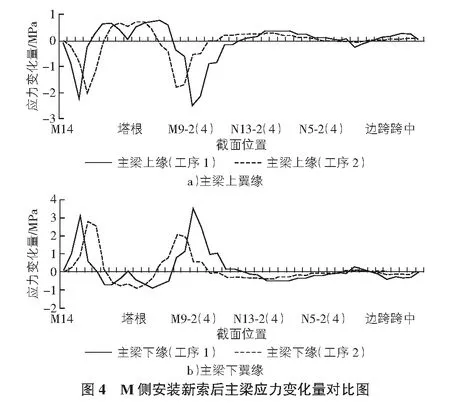
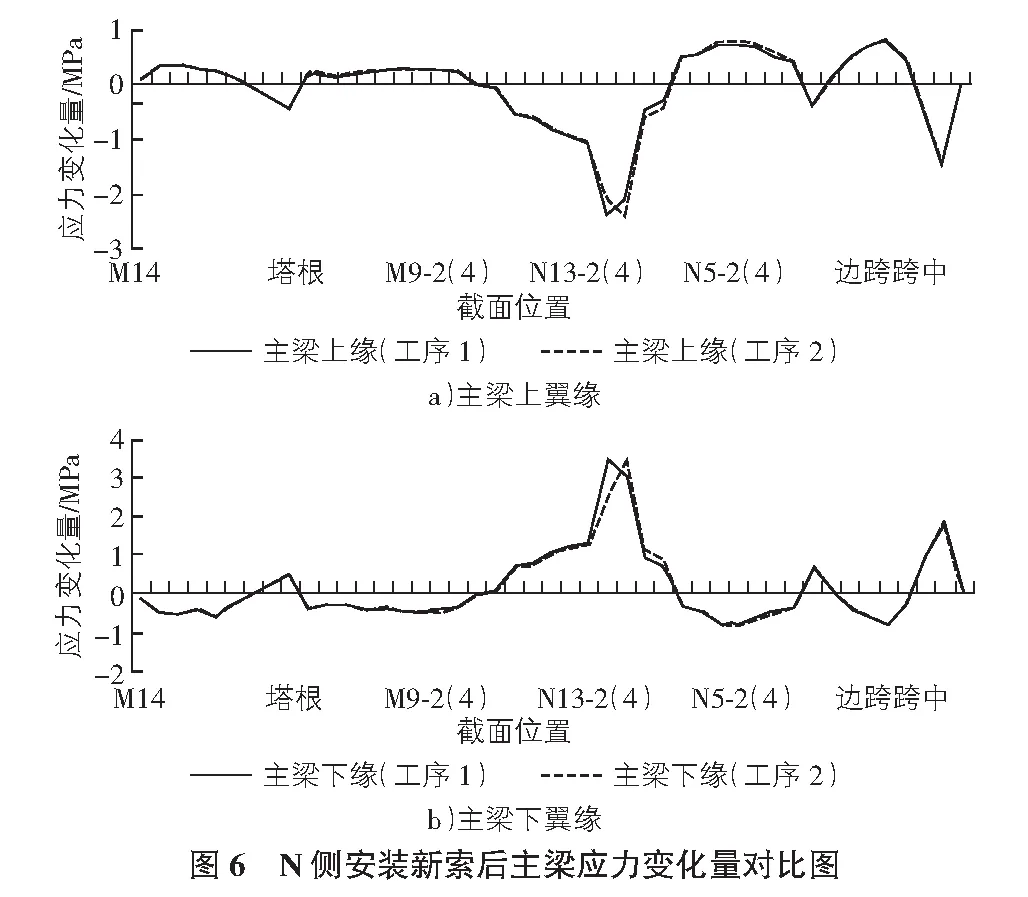
在更换N侧拉索时，主梁应力变化程度最大，对工序1来说最大施工阶段为更换N12-1，N11-1，N12-3和N11-3号索，对工序2来说为更换N12-2，N11-2，N12-4和N11-4号索，上下翼缘应力在2种工序中改变幅度最大的施工阶段对比图如图5，图6所示。

同理，从图5，图6可以看出，进行拆除、安装拉索位置附近处的主梁截面较其他位置，其应力变化量较大。从图中应力曲线峰值可以看出，两者应力变化曲线都较均匀，工序1，2均可适用。

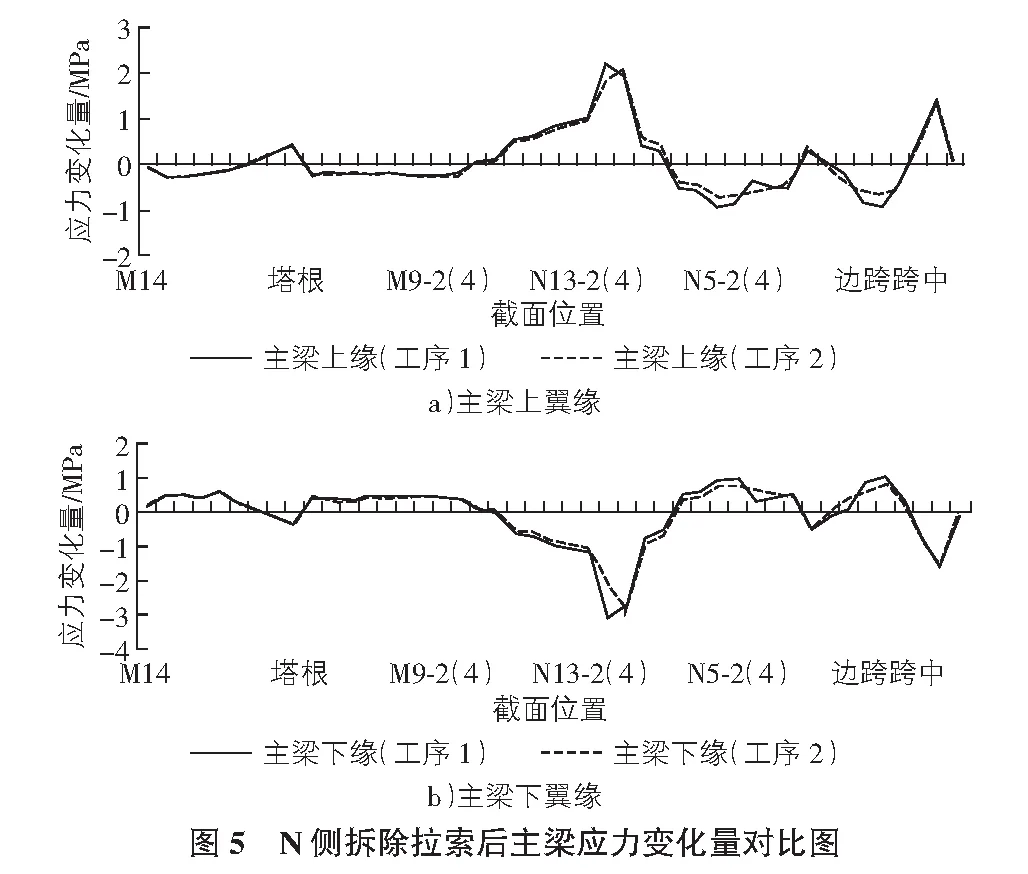
综述，不同的换索施工顺序会对主梁产生一定程度的影响，应力变化较大出现在换索施工阶段；通过上述分析可知，M侧换索适宜采用工序2，N侧换索两者皆可。

2)索塔应力影响分析。在拉索的整个施工过程中，索塔会出现偏位，索塔内力也会改变。经模型计算，在M侧更换施工时，M14-3和M13-3号索的施工产生的内力变化最大，截面应力变化量在不同截面位置变化对比图如图7，图8所示。

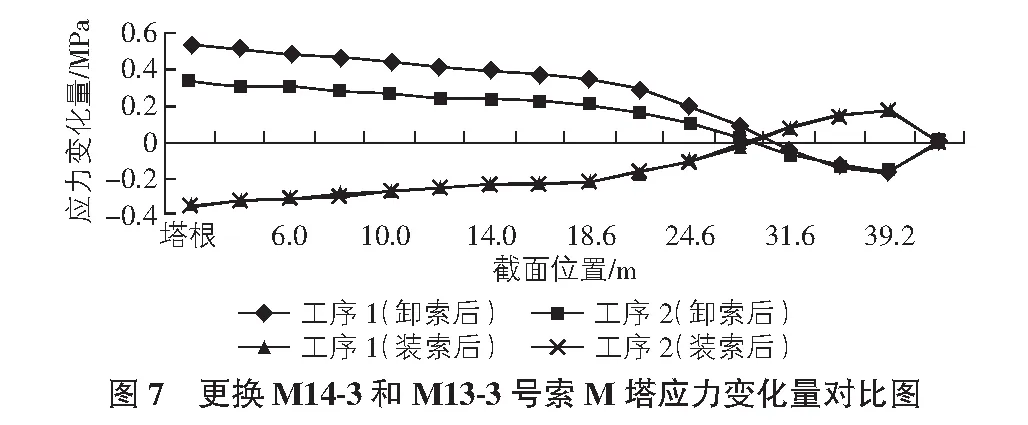
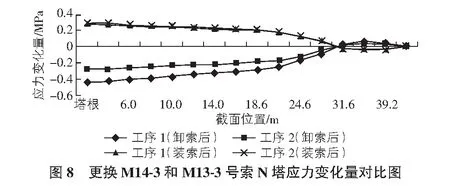
从图7，图8可以看出，不同截面位置处的索塔应力变化量不同，从塔顶向塔根递增。对比计算数据可知，在卸索时，工序1，2情况下的M，N塔根应力变化较大；工序2在整个施工过程中的应力变化量值相近，而工序1的变化幅度较大，对索塔产生的破坏也较大，所以选用工序2对索塔受力比较有利。

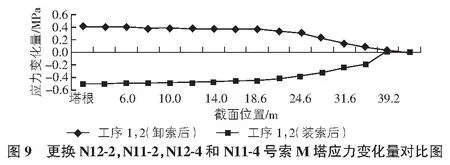
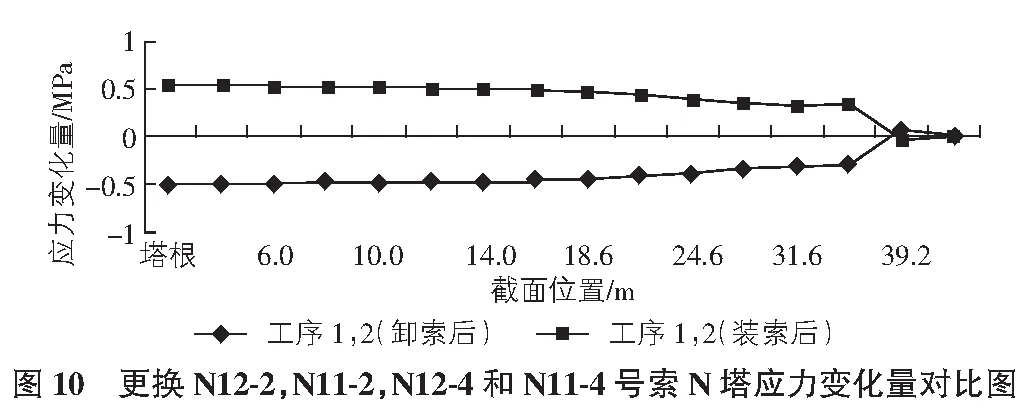
在N侧更换施工时，同样在M14-3和M13-3号索的施工产生的内力变化最大，截面应力变化量在不同截面位置变化对比图如图9，图10所示。

从图9，图10可以看出，工序1，2在更换N侧斜拉索时，索塔的应力变化量曲线相同，而且也是在塔根处索塔应力变化量最大，M侧塔应力相对变化较大，但两者相差不大；故在N侧更换斜拉索时，工序1，2均可以。

综述，采用不同的施工工序索塔应力发生较大的影响变化，从模型分析可知，工序2情况下主梁和索塔应力变化均匀，且变化较小，能保证换索的安全性和合理性，工序2较优。

3 结语

在拉索的更换中，采用逐塔换索，依据从外到内、先长索后短索的原理(即工序2)，对梁塔和主梁产生的应力变化幅度较小，换索较安全；在换索数目方面，建议在最长、最短、次长、次短索更换时以2根为最佳数目，处于中间长度的拉索更换时以4根即可，对梁塔的应力影响也较小；安全起见，不建议双塔同时进行换索施工。

[1] 谭红霞,张建民.大跨度斜拉桥施工过程索力和线性双控研究[J].河海大学学报(自然科学版),2008,36(1):97-101.

[2] Jin Cheng,Jian Jing Jiang,RuCheng Xiao,et al.Advanced aerostatic stability analysis of cable-stayed bridges using finite-element method[J].Computers and Structures,2002(80):1145-1158.

[3] 蒋伟平.斜拉桥换索理论及其技术问题的研究[D].成都：西南交通大学硕士学位论文,2003:52-54.

[4] 王文涛.斜拉桥换索工程[M].第2版.北京：人民交通出版社,2006:111-112.

[5] 谭晓琪.三达地怒江大桥换索工程实例分析[J].中外公路,2006,26(4):130-133.

The influence analysis on cable replacement construction sequence and number to beam and tower internal forces

Guo Rujiong

(CentralLake(Hainan)HaishengShippingLimitedCompanybyShare,Haikou570125,China)

Combining with the engineering situation of a bridge, this paper established the bridge plane bar system model and made simulation and calculation, combining with theoretical calculation and practice measurement, analyzed the influence of cable replacement construction sequence and number to different beam and tower internal forces, gave the best construction sequence and cable replacement number to medium and small span cable-stayed bridge cable replacement.

plane bar system, beam and tower internal force, cable replacement construction, cable replacement number

1009-6825(2016)11-0190-03

2016-01-23

郭如炯(1973- )，男，工程师

U445

A