求解配送中心选址问题的改进人工蜂群算法
姜 婷
(1.安徽经济管理学院信息工程系, 合肥 230059;2.合肥工业大学管理学院, 合肥 230009)
求解配送中心选址问题的改进人工蜂群算法
姜 婷1,2
(1.安徽经济管理学院信息工程系, 合肥 230059;2.合肥工业大学管理学院, 合肥 230009)
给出了一种改进的人工蜂群算法(IABC)用于求解配送中心的选址问题。采用自然数构建的二维矩阵对问题进行编码,提出了四种邻域生成策略。为了避免收敛速度慢和局部最优,设计了新的局部搜索算法,雇佣蜂和跟随蜂按此算法在邻域空间内更新当前解。通过仿真实验与各种智能优化算法对比,验证了提出的算法无论在有效性还是稳定性上,都具备良好的效果。
配送中心选址;改进人工蜂群;邻域生成策略;局部搜索算法
引 言
随着“互联网+”行动计划以及智能制造国家战略的提出,我国电子商务迎来了新一轮迅猛发展的机遇,智能物流是其中重要的组成部分。配送中心的建设是物流管理的起始工作,其选址问题属于战略层面的长期决策。该问题的求解是NP难题,很多学者做了相关研究,群智能优化算法的应用是其中的一个重要研究方向。文献[1-2]使用遗传算法,文献[3-4]使用蚁群算法,文献[5-6]使用混合微粒群等优化算法分别研究了物流配送中心的选址问题。
Karboga等[7]于2005年首次提出了人工蜂群算法(Artificial Bee Colony,ABC),该算法控制参数少、鲁棒性强,被应用于各种优化问题的求解中[8-12]。文献[13-14]采用基本人工蜂群算法研究了物流配送中心的选址问题。但是,研究表明,基本人工蜂群算法存在一些缺陷,如收敛能力不足、易于陷入局部极小等问题[15]。为了克服这些缺陷,很多学者提出了改进策略。王翔等[16]设计了混沌局部搜索算子及其收缩策略,实现了最优解附近的搜索并且探索范围不断减少。付丽等[17]借鉴粒子群和免疫算法思想,改进了食物源的更新方法和跟随蜂选择食物源机制。王冰[18]使用反向学习的策略对种群进行初始化,并在跟随蜂阶段引入粒子群算法进行改进。LiX等[19]、李俊青等[20]提出了邻域构建方法和局部搜索策略提高人工蜂群算法的收敛速度。陈久梅[21]提出引领蜂及其跟随蜂采用变邻域搜索策略,以此拓展蜜蜂的搜索范围。本文在已有研究基础上,提出了一种改进的蜂群算法求解物流配送中心选址问题的方法。实验表明,本文的算法具有较快的全局收敛速度,而且具有较强的有效性和稳定性。
1 配送中心选址模型
本文所研究的物流配送中心选址问题可描述为:某一物流网络中有个需求点,要从中选取个配送中心,目标是使整个物流网络的总配送费用最小。
1.1 模型假设条件
(1)从配送中心至需求点的运输费用只和运输路程的长短有关;(2)每个配送中心为多个需求点服务,每个需求点只能被一个配送中心服务;(3)需求点的需求总量不能超过配送中心的容量限制。
1.2 配送中心选址模型及参数
设配送中心集合为,需求点集合为;U为总配送费用,Fj为在需求点j建设配送中心的成本和其它固定费用,Hij为配送中心i到需求点j的单位运输费用;dj为需求点j的配送需求量;为可建的配送中心的最多个数;Mi为配送中心的容量限制。决策变量zj表示需求点是否被选中,是为1,否为0;qij表示配送中心i是否为需求点j服务,是为1,否为0。
求解的数学模型为:

s.t.
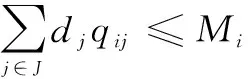
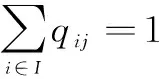
zj∈(0,1),qij∈(0,1),∀i∈I,∀j∈J
目标函数(1)表示整个物流网络的总配送费用最小,总费用包括配送中心建设成本、其它固定费用和运输费用。约束条件(2)保证建设的配送中心个数不超过限制。约束条件(3)保证配送中心服务的需求点的需求总量不超过容量限制。本文采用罚函数法来满足约束(3),即取一个非常大的正数R作为罚系数,乘上超出的容量。约束(4)保证每个需求点仅被一个配送中心服务。约束条件(5)为两个决策变量属性。
2 人工蜂群算法基本原理
人工蜂群算法是模拟工蜂的采蜜行为提出的,算法由食物源(food sources)、雇佣蜂(employed foragers)和未雇佣蜂(unemployed foragers)三个部分组成。每个食物源对应优化问题的一个可能解,其质量优劣取决于适应度值。雇佣蜂也称为引领蜂(leader),它们携带相关食物源的信息,并以若干概率向其它蜜蜂分享这些信息。非雇佣蜂分为跟随蜂(follower)和侦察蜂(scouter)两种。
人工蜂群算法的主要步骤是:
(1)蜂群初始化。整个蜂群都作为侦察蜂被派出去随机搜寻食物源。
(2)评估食物源适应度。根据适应度函数计算每个食物源的适应度(初始解)并进行排序。
(3)循环(当满足限定条件时)。
(4)雇佣蜂搜索。选择适应度高于临界值的食物源所对应的蜜蜂,将其指派为雇佣蜂。每个雇佣蜂对相应的食物源进行邻域搜索,进而找到一个新的食物源。雇佣蜂将新的食物源适应度(新解)与初始解比较,选择适应度较优的食物源。
(5)跟随蜂搜索。选择适应度低于临界值的食物源所对应的蜜蜂,将其指派为跟随蜂。跟随蜂按照食物源适应度相关的概率,采用轮盘赌方式选择一个食物源,并按雇佣蜂同样的方式对食物源进行邻域搜索。其选择食物源的概率公式为:
其中:N为食物源个数,fi是第i个食物源的适应度。雇佣蜂和跟随蜂的邻域搜索公式为:
(7)
(6)侦察蜂搜索。如果在雇佣蜂和跟随蜂的搜索过程中,食物源适应度经多次搜索未发生改变,则相应蜜蜂转换成侦察蜂。该侦察蜂将随机产生新食物源位置。
(7)评估所有蜜蜂搜得食物源的适应度并进行排序。
(8)结束。
3 求解配送中心选址问题的人工蜂群算法
3.1 问题编码
参照文献[5],本文构建的物流网络配送中心求解问题由两方面组成:(1)每个需求点是不是配送中心;(2)每个配送中心为哪几个需求点服务。本文采用自然数的编码方式构建了一个两行N列的二维矩阵,N等于需求点数量。
例如有8个需求点,从中选出3个作为物流配送中心,建立矩阵如下:
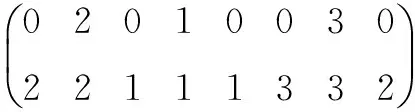
矩阵的第一行表示需求点2、4、7被选为第2、1、3的配送中心(值不为0是配送中心,为0是需求点);矩阵的第二行表示1号配送中心为需求点3、5服务,2号配送中心为需求点1、8服务,3号配送中心为需求点6服务(已被选为配送中心的不考虑)。
3.2 本文采用的改进人工蜂群算法步骤
步骤1 设置ABC算法的基本参数,主要包括:食物源规模SN(每个食物源对应一个解)、最大迭代次数MaxGen、解无改变而被丢弃的控制次数limit。
步骤2 初始化蜂群。为每个食物源分配一只雇佣蜂,每只雇佣蜂在二维空间取区间内的随机数(为配送中心数),然后对其离散化,并将记录变化次数的变量trail和迭代次数控制变量gen置0。
步骤3 根据数据模型(1)计算离散化后的每只雇佣蜂对应解的适应度。
步骤4 雇佣蜂在本文3.4部分设计的邻域范围内查找新解,如果新解的适应度优于原解适应度,则替换之,否则保持原解不变且trail加1。
步骤5 根据公式(6)计算跟随概率,跟随蜂根据该值选择对应的解,并在本文3.4部分设计的邻域范围产生新解并对其进行离散化处理;如果新解适应度优于原解适应度,则替换之,否则保持原解不变且trail加1。
步骤6 记录到目前为止适应度最高的解。
步骤7 判断trail>limit是否成立,若成立,[1~m]则侦察蜂在二维空间取区间内的随机数(为配送中心数),然后对其离散化。
步骤8 判断是否满足gen>MaxGen,若满足,则算法结束,否则转步骤(4)。
3.3 邻域生成策略
本文在文献[19]与文献[21]的基础上提出了新的邻域生成策略,雇佣蜂、跟随蜂据此生成邻域矩阵,然后进行解的更新。表1列出了四种邻域生成策略的具体示例,生成策略描述如下:
(1)交换邻域生成策略(SWAP),记为N1:在原始解内随机选择两个位置并互换数据。
(2)前插邻域生成策略(INSERT),记为N2:在原始解内随机选择两个位置,然后把后面位置的数据插入到前面数据的位置之前。
(3)倒转邻域生成策略(INVERSE),记为N3:在原始解内随机选择两个位置,然后把两个位置之间的所有数据逆序排列。
(4)相邻交换邻域生成策略(ADJACENT EXCHANGE),记为N4:在原始解内随机选择相邻的两个位置,然后互换数据。

表1 邻域生成策略示例
3.4 局部搜索算法
本文给出了一种局部搜索算法,用于在原始解周围挖掘可能的较优解,该局部搜索策略用于雇佣蜂、
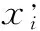
步骤1 初始化循环变量k=0,邻域矩阵neighbor为xi复制L行。
步骤2 在解空间范围内随机取两个位置r1和r2(r1≠r2),取随机数p(p=1,2,3,4),按照策略Np生成一个新解并存入邻域矩阵neighbor中。
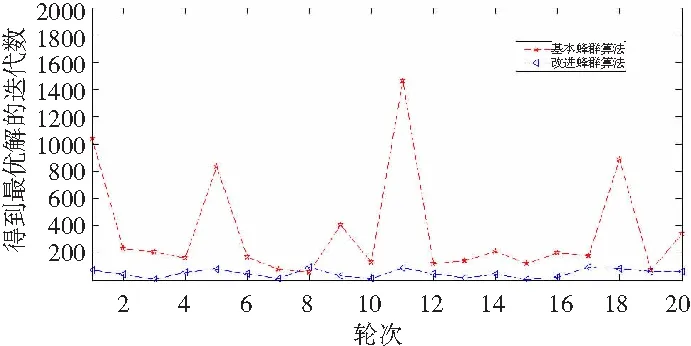
步骤3 k=k+1,若k 为验证本文算法的有效性,采用文献[5]设计的算例进行了仿真实验,部分仿真数据如表2所示。算例是从12个需求点的物流网络中选出3个配送中心,使该物流网络的总费用最小。 表2 各需求点数据 本文以Matlab R2013a为开发环境,采用Intel Core i3 2.6 GHz、4 GB的PC机,操作系统为Win7 64位。蜂群规模为80,最大迭代次数2000,同时将邻域的大小设为10。实验结果表明,该问题的最优解为161单位,被选中的配送中心编号为1、2、8,配送中心服务需求点的情况如表3所示。 表3 最优解方案 此外,在相同种群规模下和迭代次数下,GA算法、基本PSO算法、混合PSO算法、基本ABC算法、本文算法各运行20轮求解的仿真结果见表4。仿真结果表明,本文算法每次都能得到最优解161,得到最优解的平均迭代次数为52.55次,平均迭代时间为4.2326秒。可以看出,本文算法相比其它算法的有效性和稳定性都方面都更有优势。在运算时间方面,本文算法比基本PSO算法略长,但低于其他算法。 表4 各算法性能比较 本文算法由于采用了改进的邻域结构,能够稳定地得到最优解,而且平均迭代次数远小于其它算法,收敛速度有了较明显的提高,其求解配送中心选址问题的收敛曲线如图1所示。从表4中可以看出,基本ABC算法也能够在20轮求解中都得到最优解,但收敛速度较慢,需要较多的迭代次数才能得到最优解。基本人工蜂群算法和本文算法得到最优解的迭代次数比较如图2所示。 图1 采用改进ABC算法求解的收敛曲线 图2 基本蜂群算法与本文算法迭代次数比较图 本文针对物流配送中心的选址问题提出了一种改进的离散人工蜂群算法。为避免基本人工蜂群算法收敛速度较慢和陷入局部最优等问题,设计了新的邻域搜索算法,用于雇佣蜂、跟随蜂的局部寻优。通过算例实验,并与几个传统智能优化算法以及基本人工蜂群算法做了对比分析,验证了本文算法的有效性和稳定性。本文提出的算法参数较少,运行效率较高,能较好地求解配送中心选址问题。 [1] 姜大立,杜文.基于遗传算法的物流配送中心选址模型[J].物流技术,1997(5):3-6. [2] 吴兵,罗荣桂,彭伟华.基于遗传算法的物流配送中心选址研究[J].武汉理工大学学报:信息与管理工程版,2006,28(2):89-91. [3] 秦固.基于蚁群优化的多物流配送中心选址算法[J].系统工程理论与实践,2006,26(4):120-124. [4] 戢晓峰,覃文文,焦新龙,等.高强度快递需求区域移动仓库选址算法[J].交通运输工程学报,2012,12(6):69-75. [5] 李军军,王锡淮,黄有方,等.基于混合微粒群优化算法的配送中心选址问题求解[J].物流科技,2006,29(8):26-30. [6] 张玉环.基于离散粒子群算法的快递公司城市多级配送网络布局优化[J].商场现代化,2012(16):26-27. [7] KARABOGA D.An idea based on honey bee swarm for numerical optimization[R].Kayseri:Eroiyes University,Engineering Faculty,Computer Engineering Department,2005. [8] SINGH A.An Aartificial Bee Colony Algorithm for the Leaf-Constrained Minimum Spanning Tree Problem[J].Applied Soft Computing,2009,9(2):625-631. [9] PAN Q K,TASGETIREN M F,SUGANTHAN P N,et al.A discrete artificial bee colony algorithm for the lot-streaming flow shop scheduling problem[J].Information Sciences,2010,181(12):2455-2468. [10] XU Chunfan,DUAN Laibin.Artificial Bee Colony Optimized Edge Potential function approach to Target Recognition for Low-Altitude aircraft[J].Pattern Recognition Letters,2010,31(13):1759-1772. [11] OZTURK C,KARABOGA D,GORKEMLI B.Probabilisticdynamic deployment of Wireless Sensor Networks by Artificial Bee Colony Algorithm[J].Sensors,2011,11(6):6056-6065. [12] 陆欣,沈艳霞,张君继.基于人工蜂群算法的食品供应链召回优化[J].江南大学学报:自然科学版,2015,14(2):166-171. [13] 王志刚,王明刚,尚旭东.基于人工蜂群算法的配送中心选址问题求解[J].数学的实践与认识,2014,44(17):170-175. [14] 黄丽君,郭昆.收发件同步的快递服务网点选址与车辆线路规划算法研究[J].福州大学学报:自然科学版,2015,43(3):322-327. [15] AKAY B,KARABOGA D.A modified artificial for Real-Parameter Optimization[J].Information Science,2012,192(6):120-142. [16] 王翔,李志勇,许国艺,等.基于混沌局部搜索算子的人工蜂群算法[J].计算机应用,2012,32(4):1033-1036,1040. [17] 付丽,罗钧.引入跟踪搜索和免疫选择的人工蜂群算法[J].模式识别与人工智能,2013,26(7):688-694. [18] 王冰.基于局部最优解的改进人工蜂群算法[J].计算机应用研究,2014,31(4):1023-1026. [19] LI X,YIN M.A discrete artificial bee colony algorithm with composite mutationstrategies for permutation flow shop scheduling problem[J].Scientia Iranica.doi:10.1016/j.scient.2012.10.034.1921-1935. [20] 李俊青,潘全科,王法涛.求解混合流水线调度问题的离散人工蜂群算法[J].运筹与管理,2015,4(1):157-163. [21] 陈久梅,龚英.两级定位-路径问题的变邻域人工蜂群算法[J].计算机工程与应用,2014,50(6):25-30,34. Solving Location Problem of Distribution Center by an Improved Artificial Bee Colony Algorithm JIANGTing1,2 (1.Department of Information Engineering, Anhui Economic Management College, Hefei 230059, China; 2.School of Management, Hefei University of Technology, Hefei 230009, China) An improved artificial bee colony algorithm(IABC)is proposed to solve the location problem of distribution center. In the algorithm, natural number is used to construct the two-dimensional matrix of encoding problem, four neighborhood generating strategies are propposed.In order to avoid slow convergence and local optimum, a new local search algorithm is designed, by which employed bees and onlooker update the current solution in the neighborhood.Through the simulation experiment and comparison with some intelligent optimization algorithms, verify that the proposed algorithm has good performance in both effectiveness and stability. location problem of distribution center;improved artificial bee colony algorithm;neighborhood generating strategy; local search algorithm 2015-11-25 安徽省哲学社科规划项目(AHSKY2015D71);安徽省社科创新发展研究课题(A2015020);安徽省高校优秀青年人才基金重点项目(2013SQRL111ZD) 姜 婷(1976-),女,安徽滁州人,副教授,博士生,主要从事决策支持系统、群体智能等方面的研究,(E-mail)744583170@qq.com 1673-1549(2016)01-0024-05 10.11863/j.suse.2016.01.06 TP391 A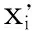
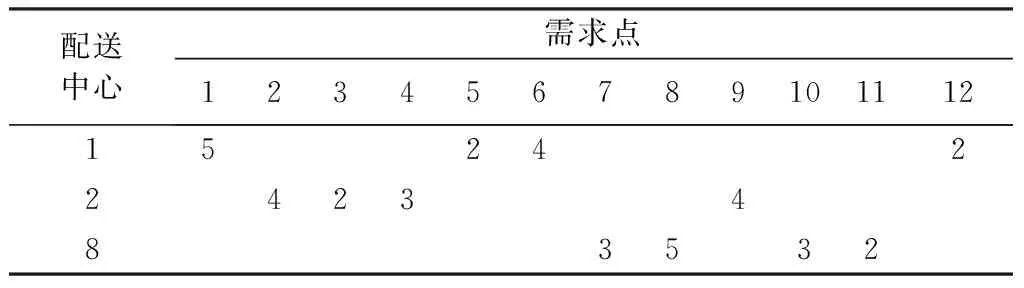
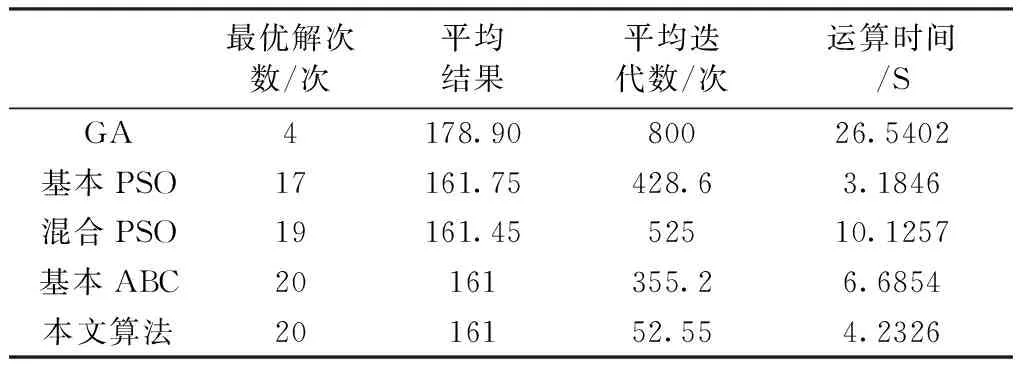
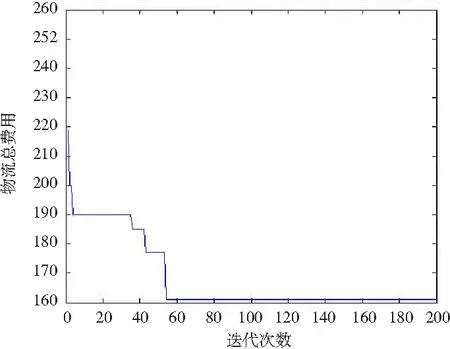
4 算例验证及结果分析

5 结束语

