奇异变换半群Singn的深度

陈辉蓉，胡华碧，龙伟峰

(1.贵州医科大学生物工程系，贵阳 550025；2.贵州师范大学数学与计算机学院，贵阳 550004)



奇异变换半群Singn的深度

陈辉蓉1，胡华碧1，龙伟峰2

(1.贵州医科大学生物工程系，贵阳 550025；2.贵州师范大学数学与计算机学院，贵阳 550004)

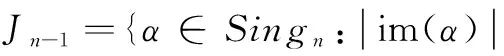
部分横截集；深度；奇异变换半群

引 言

设[n]={1,2,…,n}并赋予自然序，Tn和Sn分别是[n]上的全变换半群和对称群，称半群Singn=TnSn为[n]上的奇异变换半群[1]。奇异变换半群Singn中的 Green关系刻划[2]：

αLβ⟺im(α)=im(β)

αRβ⟺ker(α)=ker(β)

本文未定义的术语及记法见文献[3]。

1 准备工作

定义1 设A是集合[n]的一个非空子集，α∈Singn，若对任意x,y∈A,且x≠y，有xα≠yα，则称A是α在集合[n]上的部分横截集，简称A是α的部分横截集[5]。

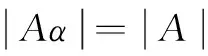
引理2 设2≤r≤n-1,则Jr·Jn-1⊆Jr∪Jr-1。

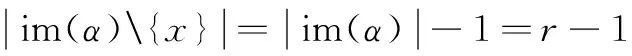
因此

αβ∈Jr-1⊆Jr∪Jr-1

综上所述，由α,β的任意性可得，Jr·Jn-1⊆Jr∪Jr-1。

引理3 设1≤s≤n-2,则Js⊆Js+1·Jn-1。

证明 任取

则β∈Js+1,γ∈Jn-1,且α=βγ，再由α的任意性可得，Js⊆Js+1·Jn-1。

引理4 设1≤r≤n-2,则Jr⊆(Jn-1)n-r。

证明 由引理3可得Js⊆Js+1·Jn-1，1≤s≤n-2,从而

Jr⊆Jr+1·Jn-1⊆(Jr+2·Jn-1)·Jn-1

⊆(Jr+3·Jn-1)·(Jn-1)2⊆…

⊆(Jn-2·Jn-1)·(Jn-1)n-r-3

⊆(Jn-1·Jn-1)·(Jn-1)n-r-2=(Jn-1)n-r

引理5 设1≤s≤n-1,则(Jn-1)s⊆Jn-1∪Jn-2∪…∪Jn-s。

证明 对s用归纳法证明。

(1)当s=1时，显然有Jn-1⊆Jn-1。

(2)假设s=k时，结论成立，即

(Jn-1)k⊆Jn-1∪Jn-2∪…∪Jn-k

当s=k+1时，由引理2及归纳假设可得，

(Jn-1)k+1=(Jn-1)k·Jn-1⊆(Jn-1∪Jn-2

∪…∪Jn-k)·Jn-1=(Jn-1·Jn-1)∪

(Jn-2·Jn-1)∪…∪(Jn-k·Jn-1)⊆

(Jn-1∪Jn-2)∪(Jn-2∪Jn-3)…

∪(Jn-k∪Jn-k-1)=Jn-1∪Jn-2∪…

∪Jn-k∪Jn-k-1

综上所述，引理5成立。

由引理5，容易得到如下推论。

推论1 设1≤s≤n-1,则

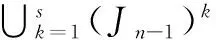
引理6 设n≥3, 则

(J1∪J2∪…∪Jn-2)∪Jn-1

⊆[(Jn-1)n-1∪(Jn-1)n-2…∪(Jn-1)2]∪Jn-1=

2 主要结果及证明

定理1 半群Singn的全Jn-1-深度为n-1。

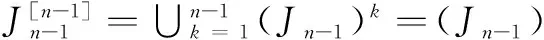
∪Jn-s⊆Jn-1∪Jn-2∪

∪J2≠Singn

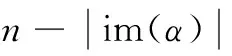
断言：存在m∈N，使Bm=φ，且当l≥m时，Bl=φ。

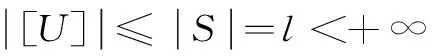
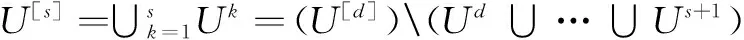
[U]Ud≠[U]

进而，d是满足条件[U]=U[k]的最小自然数，因此半群[U]的全U-深度为d。

[1] HOWIE J M.the semigroup generated by the idempotent of a full transformation semigroup[J].J.London Math.Soc.,1966,41:707-716.

[2] HOWIE J M.Products of idempotents in finite full transformation semigroup[J].Proc.R.Soc.Edinburgh.Sect.A 1980,86:243-254.

[3] HOWIE J M.An Introduction to Semigroup Theory[M].London:Academic Press,1976.

[4] HIGGINS P M.Idempotent depth in semigroups of order-preserving mappings[J].Proc.Roy.Soc.Edinburgh Sec.A,1994,124(5):1045-1058.

[5] ZHAO Ping.Maximal idempotent-generated regular subsemigroups of sopn[J].Semigroup Forum,2010,80:477-483.

[6] ZHAO Ping.A classification of maximal idempotent-generated subsemigroups of singular orientation-preserving transformation semigroups[J].Semigroup Forum,2009,79:377-384.

[7] 赵平,游泰杰,徐波.降序且保序变换半群的幂等元秩[J].山东大学学报:理学版,2011,46(4):75-77.

[8] ZHAO Ping.Semigroups of orientation-preserving transformations generated by idempotents of rankr[J].Advances in Mathematics,2010(4):443-448.

[9] 邓伟娜,裴惠生.一类变换半群中幂等元的中心化子[J].西南大学学报:自然科学版,2013(2):55-61.

[10] 李红香,赵平,游泰杰.保序变换半群On的平方幂等元[J].贵州师范大学学报:自然科学版,2014(1):48-50.

The Depth of Singular Transformation Semigroup Singn

CHENHuirong1,HUHuabi1,LONGWeifeng2

(1.Department of Bioengineering, Guizhou Medical University, Guiyang 550025, China; 2.School of Mathematics and Computing, Guizhou Normal University, Guiyang 550004, China)

partial transversal set; depth; singular transformation semigroup

2015-09-06

贵州省科学技术基金项目(KLS[2013]01)

陈辉蓉(1962-)，女，贵州仁怀人，副教授，主要从事半群理论方面的研究，(E-mail)chenghuirong1962@163.com

1673-1549(2016)01-0093-03

10.11863/j.suse.2016.01.19

O152.7

A