大跨径悬索桥反应谱分析时应考虑振型数量研究

李高超，周 琴

(1.长安大学公路学院，西安 710064；2.东北大学江河建筑学院，沈阳 110004)



大跨径悬索桥反应谱分析时应考虑振型数量研究

李高超1，周 琴2

(1.长安大学公路学院，西安 710064；2.东北大学江河建筑学院，沈阳 110004)

在使用多振型反应谱法进行抗震分析时，应先确定应该考虑的振型数，以减小计算工作量。通过某大跨径悬索桥算例，分析了不同振型参与质量系数下的反应谱计算结果。计算结果表明：对于大跨径悬索桥，规范给出的90%法则对于水平向的地震动能满足要求，且具有较高的精度；对于竖向地震的反应结果，尤其是轴力响应结果波动大，应该考虑更多的振型数计算。

大跨径悬索桥；振型数；振型参与质量系数；90%法则

引 言

大跨径桥梁往往是一个地区的地标性建筑，代表着本地区的文化特色，同时亦承担着主要的交通任务，因此在设计阶段应该考虑各种可能发生的偶然荷载和频遇荷载，以保证结构的安全性。地震即是最常见的偶然荷载之一，近几十年来国内地震发生的频率较高，因此对桥梁抗震的研究得到了长足的发展，桥梁抗震规范亦几经修订，以满足越来越多的大型复杂结构的性能需要，缆索支撑体系的桥梁的抗震性能研究亦得到了较大的发展[1-4]。《公路桥梁抗震设计细则》[5]是最新的桥梁抗震设计规范，它对桥梁的设计细则作了详细的规定。反应谱法是抗震设计的基本计算方法之一，细则规定：非规则桥梁的计算方法可以采用时程分析法或多振型反应谱法，悬索桥即属于非规则桥梁；运用多振型反应谱法计算时，所考虑的振型阶数应在计算方向获得90%以上的有效质量，即累计振型参与质量系数达到90%以上。桥梁作为一种特殊的结构，在进行抗震分析时，人们将建筑的规定直接用于桥梁结构。90%的参与系数比即来自于《建筑抗震设计规范》[6]，适用性是否适用于大跨径缆索支承体系桥梁值得商榷。李世翠等[7]介绍了90%法则的机理，同时指出对于规则的高层结构，90%的法则很容易达到，且能保证一定的精度；对于平面复杂的结构，局部震动可能存在高于90%的振动贡献的振型，建议按95%法则确定所需振型数。史铁花等[8]采用结构动力学的方法进行推导分析，提出了采用振型位移控制的方法确定振型数。王晓伟等[9]对大跨径斜拉桥进行了分析，证明了利用振型参与质量系数确定振型数在大跨斜拉桥上应用的合理性，同时亦指出水平向的地震动引起的结构反应由结构的低阶振型控制，而竖向反应由高阶振型控制，因此在计算时应取的振型数较多。

本文以一座大跨径悬索桥为工程背景，分别对其进行了顺桥向，横桥向和竖桥向的地震分析。利用多振型反应谱法，考虑不同振型参与质量系数时的地震反应，找出相应的规律。

1 振型参与质量系数

根据一般动力学知识[10-11]，很容易得到经过解耦的动力平衡方程：

(1)

在地震反应中，应该考虑设计反应谱的影响，即可得出某一方向第i阶振型产生的惯性力最大值为：

[I][M]{φ}iγiSai=

(2)

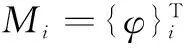
假设不考虑地震动的影响，即不考虑各阶周期在加速度反应谱上所占权重，则令式(2)中Sai=常数。根据叠加原理，各个振型对基底剪力的和等于结构的整体质量乘以整体加速度(此时各个振型的加速度谱值与整体加速度谱值相同)，可得到x、y、z方向上第i阶振型的质量参与系数表达式：

(3)

式中，Mi为第i阶振型的广义质量，∑Mj分别为x、y、z方向所有质点的质量之和。振型参与质量系数无量纲，且总和为1，是大多数程序可计算出的量，因此从使用方便的角度，将其作为确定振型数的依据。

2 实例分析

2.1 结构建模及动力特性分析

算例为一单跨悬索桥，主跨长1000 m，加劲梁为钢桁架形式。利用有限元软件SAP2000进行建模分析。其中加劲梁桁架、桥塔和吊杆采用框架单元，释放两端弯矩约束，同时施加P-Δ力考虑初拉力效应。主缆采用框架单元，施加P-Δ力考虑初拉力效应，为简化建模，边跨主缆合并为一根处理。为了考虑桩基础对结果的影响，根据文献[12]，在承台底部5倍桩径深处固结处理，桩亦采用框架单元模拟。全桥有限元模型如图1所示。

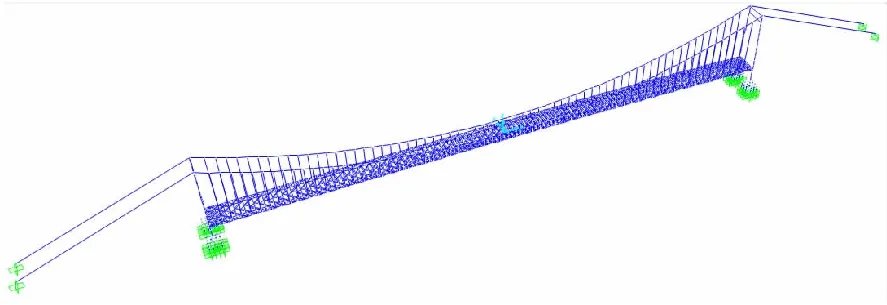
图1 全桥有限元模型图

由动力分析表1可知，大跨悬索桥的振型比较密集，振型参与质量分布比较均匀，不像常规桥梁那样一阶振型占优明显，因此在进行分析时选取计算工况时从累计振型参与质量系数40%开始，递增数值视具体情况而定，进行分析。各方向欲考虑的振型参与质量系数及相对应的振型数见表2。计算时以700阶振型为最终的考虑振型结果。从表2中可以看出，竖桥向的振型参与质量系数累计较慢，在较高振型时才会占据一定的比例。

表1 动力特性表格

表2 各方向分析工况表

2.2 地震响应分析

2.2.1 输入地震反应谱的获取

由于该场地未做地震安全性评价，因此根据细则计算得到设计反应谱，其参数：设防烈度7度，峰值加速度0.1 g，场地特征周期0.4 s，重要性系数0.43，场地土系数1，结构阻尼比取为0.02，可得到其设计反应谱曲线如图2所示。计算时分别计算顺桥向、横桥向和竖向三个方向，根据细则，竖向考虑0.65的折减系数。

图2 设计反应谱

2.2.2 结果分析

水平方向地震作用分析时，以加劲梁梁端位移，塔顶位移，塔底剪力和弯矩作为控制参数进行比较研究；竖向地震作用时以加劲梁跨中竖向位移，塔底轴力、剪力和弯矩作为控制参数进行比较研究。由于桥梁近似对称，给出一侧桥塔的值。计算结果如图3～图12所示。

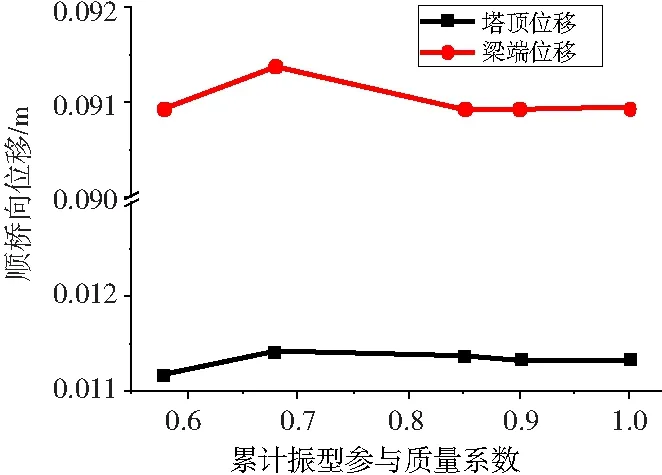
图3 顺桥向地震激励下的位移响应

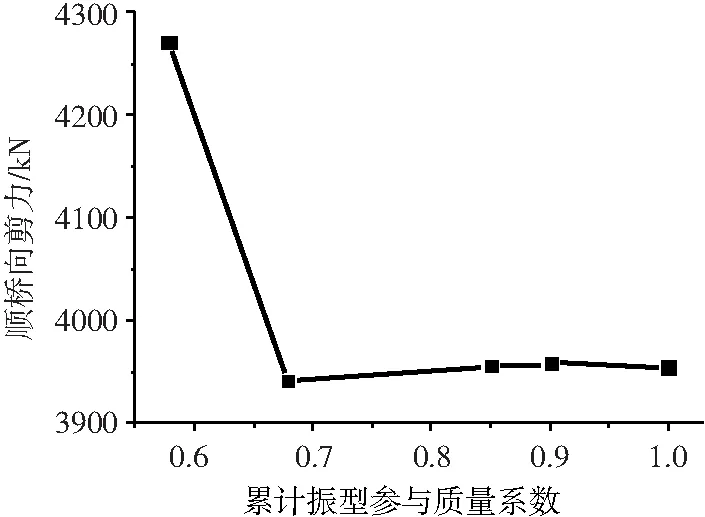
图4 顺桥向地震激励下的塔底剪力响应

图5 顺桥向地震激励下的塔底弯矩响应

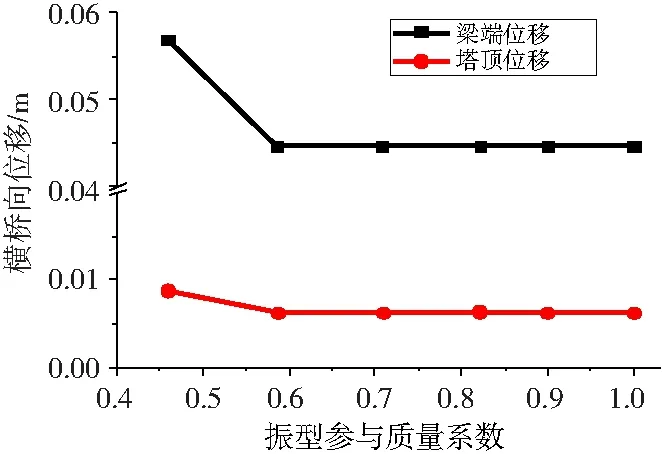
图6 横桥向地震激励下的位移响应

图7 横桥向地震激励下的塔底剪力响应

图8 横桥向地震激励下的塔底弯矩响应

图9 竖向地震激励下的加劲梁位移响应

图10 竖向地震激励下的塔底轴力响应

图11 竖向地震激励下的塔底剪力响应

图12 竖向地震激励下的塔底弯矩响应

由图3～图5可以看出，对于顺桥向的地震响应，当累计振型参与质量系数达到85%时，所得结果与考虑更多振型的结果相差较小，此时的振型编号已经排列到290，可以看出振型非常密集。同时从曲线的变化趋势可以看出，曲线并不是单调的，也从侧面反映出振型参与质量系数在60%～80%之间仍然有重要振型。

由图6～图8可以看出，对于横桥向的地震响应，当累计振型参与质量系数达到60%时，所得结果与考虑更多振型的位移和弯矩结果相差不大，而剪力值相差比较大，此时的振型编号排列为177，因此横桥向振动的阵型的密集程度低于顺桥向。从变化趋势上看，曲线不是单调变化。但是对于剪力结果在超过80%后，曲线有单调趋势，因此可以通过增大振型数提高精度。对于此桥横桥向的地震响应，90%的法则并不满足，可以通过增加振型数提高计算精度。

由图9～图12可以看出，对于竖向的地震响应，加劲梁跨中竖向位移对各种振型数取值的计算结果影响不大，对于塔的轴向力，直接受到竖向，即重力方向的惯性力影响，而惯性力与频率正相关，进而受高阶振型影响大，而且波动比较大，并不是单调的。桥塔塔底的剪力和弯矩的数值并不大，因此并不是抗震设计中的控制要素。所以只讨论轴向力的变化，其变化可能是由于竖向的累计振型参与质量增加缓慢，高阶振型的贡献效应明显，而轴向力由高阶振型控制，导致轴力结果波动较大。顺桥向、横桥向的剪力和弯矩在累计振型参与质量系数达到60%后变化不大。对于本桥在计算竖向地震响应时应该考虑超过90%的累计振型参与质量系数。

3 结 论

通过振型参与质量系数在大跨径悬索桥纵桥向、横桥向和竖桥向的地震响应，比较了根据振型参与系数确定振型数的变化情况，得出以下结论：

(1)大跨径悬索桥在三个方向的累计振型参与质量系数的增加速度是不一样的，竖向的累积速度远小于水平方向。

(2)对于大跨径悬索桥，规范规定的90%法则在一般情况下满足要求，但是在计算竖向地震作用时的轴向力响应时，尽量选取足够多的振型数计算。

(3)大跨径悬索桥振型参与质量系数分布并不是很规律，局部的振型的贡献显著，因此应考虑较多的振型数计算。

[1] 杨德健,耿辰,宋佳楠.基于多点激励下黏滞阻尼器在斜拉桥中的减震效果分析[J].世界地震工程,2015,31(2):34-42.

[2] 姜冲虎,杨博闻,李德建,等.独塔斜拉桥抗震分析及其合理约束体系研究[J].铁道科学与工程学报,2014,11(6):6-12.

[3] 燕斌,杜修力,韩强,等.减隔震混合装置在独塔斜拉桥抗震设计中的应用[J].桥梁建设,2014,44(6):101-106.

[4] 贺星新,李爱群,李建慧,等.土-桩-结构相互作用对独塔自锚式悬索桥地震响应的影响[J].东南大学学报:自然科学版,2014,44(1):150-154.

[5] JTG/F B02-01-2008,公路桥梁抗震设计细则[S].

[6] GB50011-2001,建筑抗震设计规范[S].

[7] 李世翠,聂大亮,孙斌.抗震设计合理振型数研究[J].山东建筑大学学报,2007,22(5):395-398.

[8] 史铁花,韦承基.振型分解法中合理振型数的确定[J].建筑科学,2002,18(2):29-31.

[9] 王晓伟,叶爱君.大跨度斜拉桥地震反应谱分析中计算振型数研究[J].结构工程师,2011,27(4):84-90.

[10] CHOPRA A K.Dynamics of Structures[M].USA:Prentice-Hall,2000.

[11] CLOUGH R W,Penzion J.Dynamics of Structures[M].2nd Edition.USA:McGraw-Hill,1995.

[12] 叶爱君,管仲国.桥梁抗震[M].北京:人民交通出版社,2002.

Study on Number of Response Spectra Analysis Mode for Long Span Suspension Bridge

LIGaochao1,ZHOUQin2

(1.School of Highway, Chang’an University, Xi’an 710064, China; 2.JangHo Architecture College of Northeastern University, Shenyang 110004, China)

In using multi mode response spectrum method for seismic analysis, the number of modes should be firstly considered in order to reduced computational work load. Taking a long span suspension bridge as an example, the calculation results of the response spectrum of different type of vibration modes are annlyzed. The calculation results show that for long span suspension bridge, the 90% rules given by the specification can meet the requirements of horizontal seismic energy and have high psecision; for vertical seismic response results, especially the result of the axial force response, more modes should be considered.

long span suspension bridge; mode number; modal participation mass ratio; 90% rules

2015-10-27

李高超(1990-)，男，陕西西安人，硕士生，主要从事桥梁抗震与抗风方面的研究，(E-mail) 1277707155@qq.com

1673-1549(2016)01-0082-05

10.11863/j.suse.2016.01.17

U442.55

A