两无穷区间上积分交换次序充分条件的改进及其应用

邢家省，杨小远，白 璐

(1.北京航空航天大学数学与系统科学学院，北京 100191；2.数学、信息与行为教育部重点实验室，北京 100191)



两无穷区间上积分交换次序充分条件的改进及其应用

邢家省1,2，杨小远1,2，白 璐1,2

(1.北京航空航天大学数学与系统科学学院，北京 100191；2.数学、信息与行为教育部重点实验室，北京 100191)

考虑两无穷区间上的积分交换次序定理的充分条件问题，指出了数学分析中经典定理的充分条件的不足和局限性、适用范围有限、解决问题困难等问题。对经典的充分条件在表述条件上给予改进，并运用数学分析中积分控制收敛定理给予证明，达到了数学分析中应有的理论高度，从而得到新结果。通过实例比较，使用新的积分交换次序定理更方便于验证条件。

无穷区间上的积分交换次序定理；含参变量广义积分；内闭一致收敛性；比较判别法；控制收敛定理

两无穷区间上的积分交换次序定理[1-12]是数学分析中的重要结果，在文献[1-7]中，给出了两无穷区间上的积分可交换积分次序的充分条件和证明过程。发现数学分析中的积分交换次序定理的经典充分条件在实际问题中很难满足，对许多不满足此充分条件的函数不能直接利用[2，8]，对有些函数验证满足经典充分条件也繁琐[1-2]。将经典的充分条件给予改进，在广泛的充分条件下给出积分交换次序定理的结果，得到最好的理论表现形式，并且在导出结果的过程中没有增加任何理论难度，利用新的表述结果可以更方便解决一批函数的积分计算问题。经典的积分交换次序定理中充分条件的局限性问题在文献[2，8]中已探讨，由于直接套用很困难，因而采用其他复杂的解决方法，其实，可以将原有理论结果发展，达到数学分析学中应有的理论高度和广泛适用性。

1 无穷区间上积分交换次序定理的经典充分条件及其局限性

定理1[1-7](无穷区间的积分交换次序)设函数f(x,u)在[a,+∞)×[α,+∞)上连续，如果满足下列条件：

定理1是标准数学分析教材中的经典结果[1-7]。可以发现，定理1中充分条件(1)是苛刻的，对有些函数的验证很困难，有些函数也不满足此条件，不能直接套用此定理。可以将定理1中的条件(1)改进为一般形式，得到更好的一般结果形式，新的结果更方便使用。

定理2[1-7](无穷区间上的积分交换次序)如果函数f(x,u)满足条件：

(1)f(x,u)在[a,+∞)×[α,+∞)上连续且非负。

定理2中的条件(2)也有局限性，适用范围有限。

2 无穷区间上积分交换次序的充分条件的改进条件

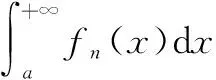
如果满足条件：

(1)对任意A>δ>a，{fn(x)}在[δ,A]上一致收敛于f(x)。

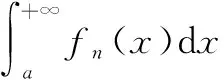
注意这里的积分下限a可能是积分的瑕点，a也可能是-∞。

定理3常被使用的情形是控制收敛定理。

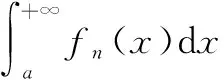
如果满足：

(1)对任意A>δ>a，{fn(x)}在[δ,A]上一致收敛于f(x)。

定理4虽然是以函数列的极限形式叙述的，完全可以写出其他极限形式的相应结论[3,5,9]。

定理5 (无穷区间上的积分交换次序)设函数f(x,u)在(a,+∞)×(α,+∞)上连续，如果满足条件：

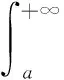
记

显然

因此，证明了结论。

显然定理5的条件比定理1的条件广泛自然，也就是定理5的结果优于定理1的结果，完全应该采用定理5替代定理1，数学分析中应该以定理5的结果为最终形式，为得此结果，证明过程没有增加任何困难，定理5的充分条件，在实际应用中非常方便于验证，减少了解决问题的难度。

文献[1-9]中的狄尼定理也可以改进为如下形式。

定理6 (狄尼定理)如果函数f(x,u)满足条件：

(1)f(x,u)在(a,+∞)×(α,+∞)上连续且非负。

一般地，对(a,b)×(c,d)上的积分交换次序定理的充分条件类似的可以给出，这里下限a,c可以是有限的或为-∞，上限b,d可以是有限的或为+∞。

3 一些含参变量广义积分的一致收敛性

证法2注意到

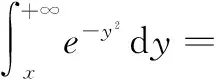
于是对A>0，成立

证明 由

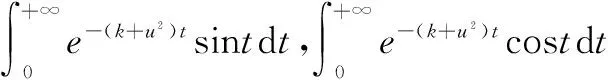
定理13[1-9]成立

4 利用无穷区间上积分交换次序定理计算广义积分的方法

令f(t,u)=ue-u2(1+t2)，则有f(t,u)在[0,+∞)×[0,+∞)上是连续且非负的。

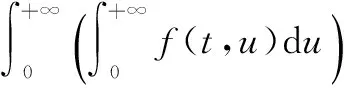
故由定理5，交换积分次序是允许的，于是

所以

注意

e-u2I,(u>0)，φ(u)在(0,+∞)

函数f(t,u)=ue-u2(1+t2)在[0,+∞)×[0,+∞)上不满足定理1的条件，也不满足定理2的条件，但满足定理5和定理6的条件。

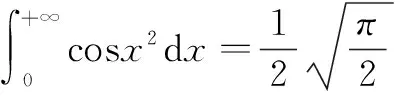
证明 命x2=t，那么

(1)

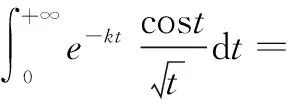
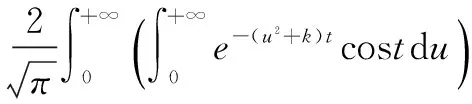
记f(t,u)=e-(u2+k)tcost，(k>0)。

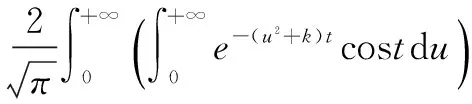
(2)

所以，有

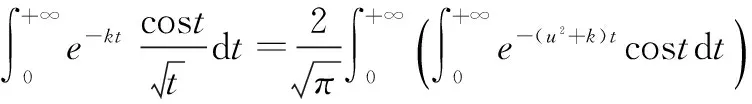
(3)

故有

注意函数f(t,u)=e-(u2+k)tcost在[0,+∞)×[0,+∞)上不满足定理1的条件。

类似的，可以给出：

函数f(t,u)=e-(u2+k)tsint在[0,+∞)×[0,+∞)上满足定理1的条件，但验证比较复杂[1-2]。验证函数f(t,u)=e-(u2+k)tsint在[0,+∞)×[0,+∞)上满足定理5的条件就非常容易。

定理17[2]设α为实常数，则成立

(4)

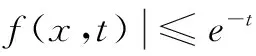
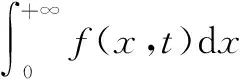
在文献[2]中，为了证明(4)式成立，给出了相当繁琐的证明过程。

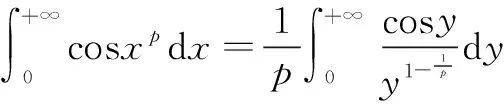
于是

记

(t,y)∈(0,+∞)×(0,+∞)

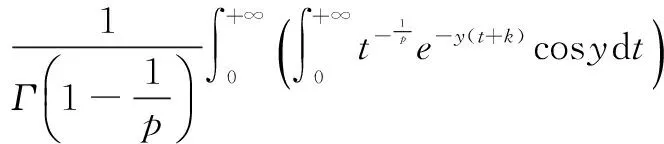
(5)

式(5)两端令k→0+，即得

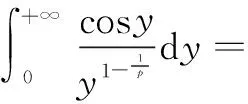
故

[1] 常庚哲,史济怀.数学分析教程(下册)[M].北京:高等教育出版社,2003.

[2] 黄玉民,李成章.数学分析(下册)[M].2版.北京:科学出版社,2007.

[3] 华罗庚,著.王元,校.高等数学引论(第二册)[M].北京:科学出版社,2009.

[4] 复旦大学数学系.数学分析(下册)[M].北京:高等教育出版社,1988.

[5] 张筑生.数学分析新讲(第三册)[M].北京:北京大学出版社,1990.

[6] 华东师范大学数学系.数学分析[M].北京:高等教育出版社,2001.

[7] 陈纪修,於崇华,金路.数学分析(下册)[M].2版.北京:高等教育出版社,2003.

[8] 费定晖,周学圣.吉米多维奇数学分析习题集题解(五)[M].济南:山东科学技术出版社,1980.

[9] 裴礼文.数学分析中的典型问题与方法[M].北京:高等教育出版社,2002.

[10] 匡继昌.Dirichlet积分九种解法的思路分析[J].高等数学研究,2012,15(4):61-64.

[11] 黄丽云.被积函数正负性周期变化的反常积分[J].高等数学研究,2013,16(6):9-10.

[12] 宋文章.无界函数的反常积分的计算[J].高等数学研究,2014,17(6):19-21.

Improvement and Application of Sufficient Condition of Integrals Exchange on Two Infinite Interval

XINGJiasheng,YANGXiaoyuan,BAILu

(1.College of Mathematics and System Science, Beihang University, Beijing 100191, China;2.Key Laboratory of Mathematics, Information and Behavior, Ministry of Education, Beijing 100191, China)

Considered the sufficient condition of integrals exchange theorem on two infinite intervals, the shortage and limitation of the sufficient condition of classic theorem in mathematical analysis was put forward. Because of the limited range of application, difficulty of solving problem, the expression of classic sufficient condition was proved by the integral dominated convergence theorem of mathematical analysis. Then the proper theoretical height in mathematical analysis was achieved, and a better theoretical result was obtained.Via comparing the examples, it was very convenience to verify the conditions using the new integrals exchange theorem.

integrals exchange theorem on infinite interval; generalized integral contained parameters; inner close uniform convergence; comparison discriminance; dominated convergence theorem

2015-10-22

国家自然科学基金项目(61271010)；北京航空航天大学校级重大教改项目(201401)

邢家省(1964-)，男，河南泌阳人，副教授，博士，主要从事偏微分方程、微分几何方面的研究，(E-mail)xjsh@buaa.edu.cn;

杨小远(1964-)，女，辽宁沈阳人，教授，博导，主要从事应用调和分析、图像处理方面的研究，(E-mail)xiaoyuanyang@buaa.edu.cn

1673-1549(2016)01-0087-06

10.11863/j.suse.2016.01.18

O177.2

A