分子动力学模拟3(5)-(9-蒽基)吡唑分子在自组装膜上的选择性沉积

张鲁格, 薛泽旭, 张 翀, 延 辉

(1. 聊城大学化学化工学院, 2. 药学院, 聊城 252059)



分子动力学模拟3(5)-(9-蒽基)吡唑分子在自组装膜上的选择性沉积

张鲁格1, 薛泽旭1, 张 翀1, 延 辉2

(1. 聊城大学化学化工学院, 2. 药学院, 聊城 252059)

采用平衡分子动力学和拉伸分子动力学模拟方法研究了模板诱导有机发光小分子3(5)-(9-蒽基)吡唑(ANP) 在自组装膜上的选择性沉积, 并利用伞形取样方法和加权柱状图分析法计算了沉积过程的均力势. 模拟中以二氧化硅为底板分别构筑2种不同密度的烷烃链自组装膜模板, 即低密度的液体扩展相和高密度的液体压缩相. 平衡分子动力学结果显示, ANP分子容易沉积至低密度的液体扩展相中, 难以沉积至高密度的液体压缩相中. 拉伸分子动力学结果表明, 当ANP分子沉积至液体压缩相表面时, 在进入烷烃膜时遇到较大阻力, 因而不易进入到烷烃链单层膜中; 而ANP分子在进入液体扩展相的过程中受到的阻力较小. 通过比较这2种不同密度自组装膜与ANP分子之间的结合自由能, 发现ANP分子进入液体压缩相的能垒较高, 而ANP分子与液体扩展相结合更加稳定, 导致有机发光小分子在不同密度的模板上具有选择吸附性. 所得模拟结果与实验现象一致, 在分子水平上为实验提供了更加丰富的微观信息.

自组装膜(SAM); 定位沉积; 拉伸分子动力学; 伞形取样; 3(5)-(9-蒽基)吡唑; 低密度的液体扩展相; 高密度的液体压缩相; 均力势

微纳尺度有机发光小分子定位沉积形成的图案在光学[1]、 光电子学[2]、 生物芯片的检测[3]、 生物传感器的重排[4]及相关领域都有广泛应用, 因此表面图案的构筑是一个重要的研究课题. 最近Chi等[5～9]利用Langmuir-Blodgett(LB)技术在石英表面得到液体扩展相(Liquid expanded, LE)和液体压缩相(Liquid condensed, LC)交替排列的二棕榈酰磷脂酰胆碱膜(DPPC)条带图案结构,这种条带图案结构可以作为模板诱导无机[10,11]或有机[9]分子在气相中选择性沉积. 如, 少量的有机荧光分子3(5)-(9-蒽基)吡唑(ANP)[9]或芘分子[6]会优先沉积在DPPC膜的液体扩展相(LE)上, 而随着ANP分子增多形成较大聚集颗粒时, 一些ANP分子开始沉积在液体压缩相(LC). ANP分子在这种条带结构上的定位沉积是一个扩散成核和生长的过程. 除了这种疏密相间的DPPC自组装膜条带结构以外, 由烷烃链连接在基底上形成的自组装单分子膜(Self-assembled monolayers, SAMs)对有机发光小分子也具有相似的选择性吸附[12,13]. 因此理解模板诱导有机发光小分子定位沉积机理, 对于设计和开发新型选择性吸附单层膜材料非常有益.

选择性吸附现象和发光小分子与不同密度自组装膜之间的结合能有关. Chi等[5]依据原子力显微镜测量数据推测有机发光小分子在液体扩展相和液体压缩相之间迁移所需要克服的能垒不同, 因而造成了发光小分子在薄膜上的选择性吸附, 这一推测在其随后的分子模拟研究中得到证实[14]. 一系列的模拟结果表明, 发光小分子包括ANP和苝等在液体扩展相和液体压缩相之间迁移扩散同时受到自组装膜密度和柔性的影响. 此外, 对于固体表面自组装膜的相行为以及自组装膜吸附发光小分子的理论研究[15～18],也获得了与实验结果一致的结构信息.

上述实验和理论研究工作能够帮助我们更好地理解发光小分子在模板上定位沉积本质, 但是在分子水平上对实验现象的解释仍有待加强, 特别是针对有机发光分子沉积吸附过程中自由能的计算. 这是由于探讨小分子和自组装膜结合能力强弱的一个重要依据就是二者之间的相互作用, 因此从能量的角度来研究小分子在自组装膜上的沉积吸附是对宏观实验的重要补充. 近年来, 拉伸分子动力学(Steered Molecular Dynamics, SMD)[19]和伞形取样方法(Umbrella sampling method)[20]常被用来研究分子间的相互作用, 依据均力势(Potential of mean force, PMF)来判断吸附过程中的结合位点或结合构象等微观信息[21～24].

本文采用平衡动力学和非平衡动力学(拉伸分子动力学)相结合的方法, 研究有机发光小分子3(5)-(9-蒽基)吡唑(ANP)在2种不同密度单分子膜上的选择性沉积. 首先, 运用平衡分子动力学来研究ANP分子在不同密度单分子膜上的沉积行为, 得到平衡状态下ANP分子在自组装膜上的吸附位点及构象. 其次, 采用拉伸分子动力学方法将ANP分子拉伸至烷烃链单分子膜中, 用伞形取样方法和加权柱状图分析法(Weighted histogram analysis method, WHAM)[25]计算ANP沉积至不同密度单分子膜的过程中的自由能, 在分子水平上解释发光分子选择性沉积的本质, 为基于发光分子定位沉积的表面图案构筑提供一定的理论帮助.

1 模型与方法

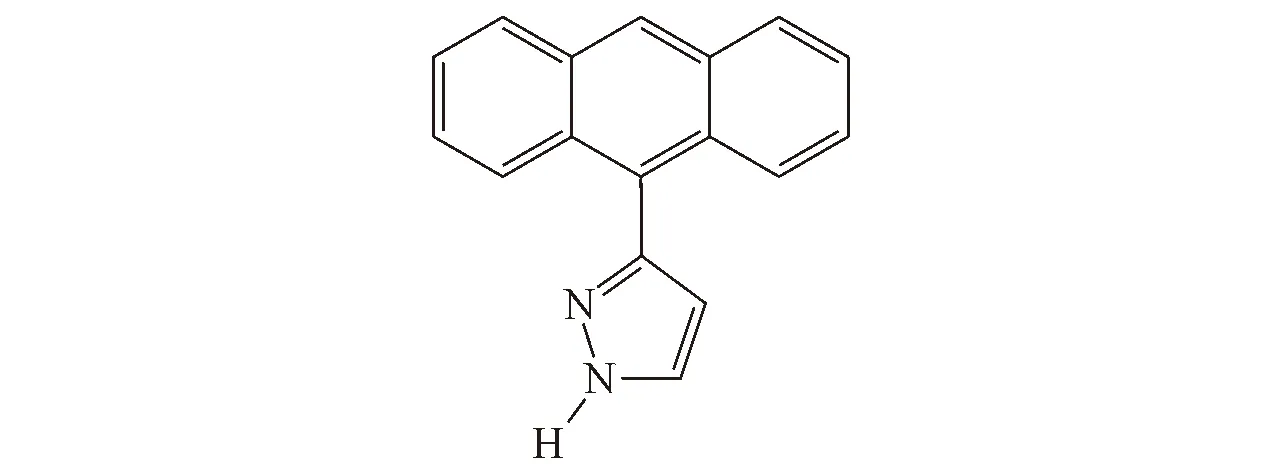
Fig.1 Chemical structure of 3(5)-(9-anthryl) pyrazole(ANP)

依据文献[15,26,27]的方法, 将十八烷烃链以C-Si共价键连接在α-石英晶体(100)晶面形成自组装单分子膜(SAMs)上, 并通过改变烷烃链的个数得到2种不同密度的自组装膜. 密度较高的自组装膜含有64个烷烃链, 二氧化硅表面单分子链占据面积约为0.265 nm2, 这与文献[15]的结果一致; 而低密度的自组装膜则含有32个烷烃链. 这2种自组装膜的模型分别用以模拟实验报道的液体压缩相和液体扩展相[5]. 对于低密度自组装膜, 我们构建了另外3种不同烷烃链排列方式的模型来讨论其对小分子沉积过程的影响. 表面所有的未饱和硅原子均采用羟基化处理. 模拟中在x, y, z 3个方向上使用周期性边界条件, 同时为消除z方向上镜像对周期性结构的影响, 模拟格子大小选择为3.93 nm×4.32 nm×10.42 nm. 首先对这2种密度自组装膜体系在NVT系综下进行5 ns的分子动力学模拟, 得到二氧化硅表面自组装膜的稳定构型. 然后将一个ANP分子(图1)分别放置在距离这2种烷烃分子层膜表面约2 nm的位置, 以此作为平衡和拉伸分子动力学模拟模板吸附沉积ANP分子的初始构型.

本文所采用的平衡分子动力学模拟即传统分子动力学方法, 其采用经验势函数表征分子间相互作用, 通过求解牛顿力学方程来模拟分子体系的运动. 模拟中势函数选取OPLS-AA力场[28],使用GROMACS 4.6.3软件包[29]进行分子动力学计算. 力场中的势能函数包括成键伸缩势、 键角弯曲势、 离平面势和非键相互作用势, 其中非键相互作用包括 Lennard-Jones 势和库伦作用势. 利用GAMESS(US)程序包[30], 在B3LYP/6-31G水平上计算得到ANP分子的原子静电势电荷(ESP)作为力场中的库伦作用项. 基底二氧化硅的相关力场参数来自文献[31]. 详细的力场参数列于表S1(见本文支持信息). 初始构型建立以后, 对所有体系首先利用最速下降法进行能量最小化以消除可能的构象重叠, 然后在NVT系综下进行5 ns分子动力学模拟, 其中模拟步长为1 fs. 模拟过程中对基底二氧化硅在x, y, z 3个方向进行约束. 体系温度采用Berendsen方法[32]控制在298 K. 体系中所有分子键长均采用LINCS算法[33]约束. 短程非键作用势能截断半径设置为1.2 nm. 采用Particle-mesh Ewald(PME)方法[34]处理长程静电相互作用. 使用VMD 1.9.1软件[35]观察动力学轨迹.

拉伸分子动力学方法是一种非平衡动力学模拟方法, 在模拟过程中对目标原子或基团沿着给定的方向施加外力, 从而加速构象变化的进程. 该方法可分为恒速和恒力2种方式, 本文采用恒速拉伸模拟方法, 即在模拟中对拉伸分子施加外力的大小不断变化. 在受阻小的区域外力小, 而在受阻大的区域所需外力大, 以此保证移动速度恒定不变. 拉伸模拟所采用的初始构型和平衡动力学方法一致, 通过对ANP分子沿着靠近自组装膜方向施加一个外力, 以加速ANP分子沉积吸附过程. 其中弹簧弹性系数和拉伸速度是影响模拟结果准确性的重要因素. 为保证拉伸过程中拉伸区域的正常分离和取样, 我们结合文献[20～23]报道将拉伸弹簧弹性系数设定为1000 kJ·mol-1·nm-2, 而对于拉伸速度则考察了4个条件, 即0.001, 0.0025, 0.005和 0.01 nm/ps. 基于SMD模拟获得的吸附路径中的特定结构, 采用伞形取样法和加权柱状图分析法(WHAM)计算这一过程的平均力势能. 其中, 反应坐标为ANP分子质心沿着垂直于二氧化硅基底表面方向的距离变化(总距离约为3.0 nm). 为了提高计算效率, 整个反应坐标被分成长度为0.2 nm的若干个窗口. 在每个窗口内都进行5 ns的取样模拟, 并在模拟中对体系施加偏置势能(1000 kJ·mol-1·nm-2)加以限制. 拉伸模拟和取样模拟中的其它计算细节与平衡动力学模拟一致.

2 结果与讨论

2.1 ANP分子在2种不同密度SAMs中的沉积构型

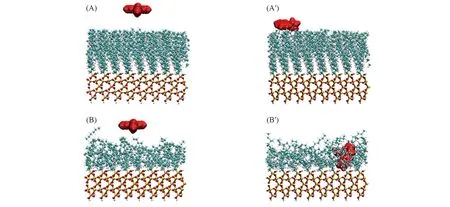
Fig.2 Configurations of ANP deposited on LC(A, A′) and LE(B, B′) phases at the initial(A, B) and the end(5 ns, A′, B′) of the MD simulation

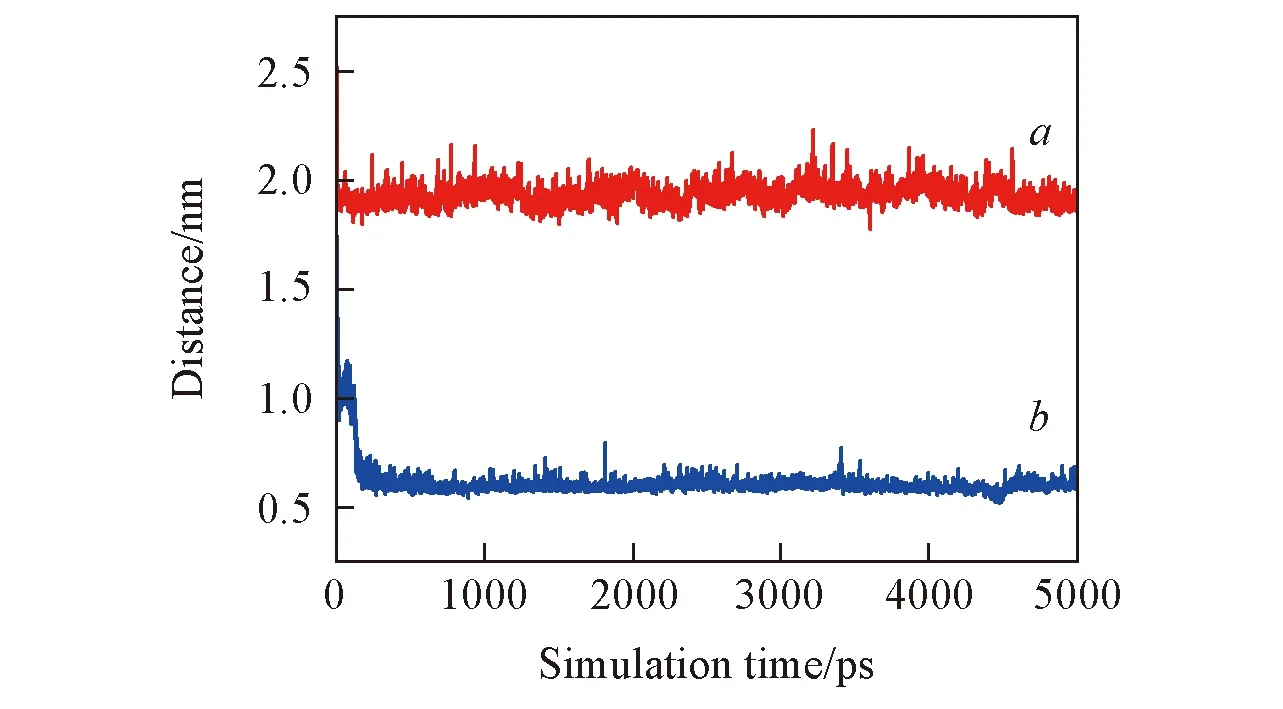
Fig.3 Time profiles of the vertical distance between the COM(center of mass) of the ANP molecule and the surface of the SiO2 substratea. LC phase; b. LE phase.

为了考察ANP分子在液体压缩相(LC)和液体扩展相(LE)2种模板上沉积的稳定结构, 对平衡分子动力学结果进行分析. 图2给出了2种体系的初始和终态构型. 通过对比, 可以直观地看到ANP分子在2种不同组装密度SAMs上沉积的差异: ANP分子并未沉积嵌入LC膜的烷烃链区域而是吸附在烷烃链单层膜的表面; 而对于LE相, ANP分子则沉积在了烷烃链单层膜中. 同时, 发现LC相中的烷烃链排列较为致密有序, 而LE相中烷烃链则由于倒伏则相对稀疏散乱. 正是由于LC相中烷烃链密度较高同时排列紧密, 阻碍了ANP分子进入到单层膜中. 通过计算ANP分子质心和SiO2基底表面之间垂直距离随模拟时间的变化可以反映出小分子的沉积过程, 结果如图3所示. 从距离变化可以看出, ANP分子在很短的模拟时间内就可以吸附至烷烃链分子层膜表面. 而随着模拟的进行, ANP分子稳定保持在距离LC相基底表面约2.0 nm的位置处, 也就是烷烃链膜表面. 而在LE相中, ANP分子质心和基底表面距离稳定保持在约0.6 nm处. 距离变化在模拟的最后4.5 ns中保持稳定也反映出模拟体系达到了平衡.

2.2 自组装膜密度对ANP沉积位点的影响

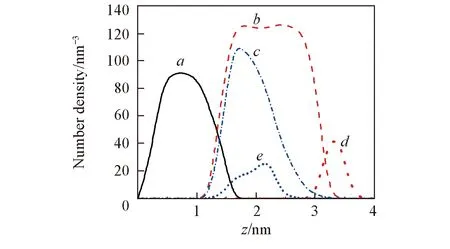
Fig.4 Number density profiles of components for LC and LE systemsa. SiO2; b. LC; c. LE; d. LC-ANP; e. LE-ANP. Values for ANP atoms were multiplied by 10 for clarity.

ANP分子在LC和LE相中沉积位点有明显的不同, 这种现象应该与这2种膜中烷烃链的密度有关. 通过计算相关组分的密度分布考察了LC和LE相烷烃链的结构特点. 密度分布是通过计算LC和LE相体系中各组分沿z轴方向(即垂直于自组装膜表面方向)的单位体积内的数量, 图4给出了统计平均最后3 ns轨迹所得曲线图. 所计算的各个组分包括SiO2基底, 烷烃链以及ANP分子. 从图4可以估算出LC相和LE相中烷烃链膜的厚度, 其中LC膜的厚度约为2.0 nm. 而在这2.0 nm范围内密度分布较为均匀说明烷烃链排列比较致密有序. 对于LE相, 烷烃链的密度分布从SiO2基底表面延伸至3.0 nm, 在距离基底表面约1.0 nm处有一个明显的峰值. 这说明LE相中的烷烃链分子向SiO2基底表面弯曲倒伏, 造成了靠近基底表面的烷烃密度较大, 自组装膜表面烷烃链密度较小. 相比LC膜的密度, LE相中的烷烃链密度峰值强度降低, 说明在LE相中烷烃链膜间存在分子间隙. 这些分子间隙为ANP沉积吸附至SiO2基底表面提供了可能的空间.

由ANP分子的密度分布可以更为直观地显示其在自组装膜中的沉积位点. 从图4可见, ANP分子集中分布在LC相烷烃链密度分布范围以外, 即, ANP分子沉积在烷烃链膜表面. 在LE相中, ANP分子的密度分布和烷烃链的分布位置几乎重叠, 表明ANP分子进入了烷烃链区域内部. 不同烷烃链排列方式的LE相吸附ANP分子的距离和密度分布见图5. 从图5可以看出, 不同排列方式下ANP分子都能沉积至自组装膜内部区域. 而质心和基底表面的距离存在一定的误差(约0.25 nm), 这是由于LE相中膜的密度并不均匀且ANP分子质心变化范围较大所致. 尽管ANP分子距离基底表面距离稍有不同, 但是ANP分子均沉积在自组装膜表面烷烃链密度较小的区域.

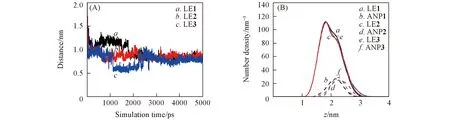
Fig.5 Results from simulations started with different initial configurations for the LE system(A) Time profiles of distance; (B) number density profiles (values for ANP atoms were multiplied by 10 for clarity).

2.3 拉伸分子动力学模拟ANP分子沉积过程

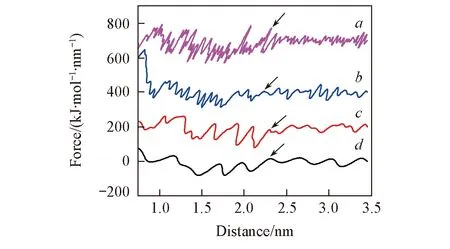
Fig.6 Distance profiles of force using different pulling ratesVertical shifts of 200, 400 and 700 units were imposed for profiles at rates of 0.005, 0.0025 and 0.001 nm/ps, respectively. V/(nm·ps-1): a. 0.001; b. 0.0025; c. 0.005; d. 0.01.

对于拉伸分子动力学模拟, 拉伸速度可能会对模拟结果产生影响[24]. 本文在确定弹簧系数(1000 kJ·mol-1·nm-2)的条件下, 考察了几种不同的拉伸速度对拉力曲线的影响. 以ANP分子在LE相沉积的体系为例, 考察4组不同速度下的拉伸实验(0.001, 0.0025, 0.005和0.01 nm/ps), 拉伸距离约为3.0 nm. 不同拉伸速度下拉力随拉伸距离变化曲线如图6所示. 从图6可见, 在不同的拉伸速度下, 外力大小的变化趋势几乎是一致的. 即在拉伸模拟的开始阶段, 各拉伸速度下的受力均保持相对稳定. 通过观察拉伸分子动力学轨迹, 发现ANP分子在外力的作用下逐渐靠近烷烃链分子层膜表面. 而当ANP分子开始进入分子层膜中时[图6箭头所示, 所对应构型图(图S1)见本文支持信息], 拉力开始出现较大的波动. 这是由于ANP分子在进入单层膜时受到了烷烃链的空间阻力, 外力需要克服阻力才能够使ANP分子移动. 不同拉伸速度的模拟构型随时间的变化见图S1, 综合考察构型和受力的变化趋势, 可以看出, 在一定范围内选取拉伸速度对于ANP分子的沉积过程影响很小. 而更高或更低的拉伸速度则会影响取样分析或降低计算效率.

以0.005 nm/ps拉伸速度为例, 说明ANP分子在SMD模拟过程中的吸附行为, 图7给出了ANP分子沉积至液体压缩相(LC)过程中具有代表性的构型, ANP分子在液体扩展相(LE)中沉积的SMD模拟构型见图S2(见本文支持信息). 对于LE相体系, ANP分子的沉积过程和平衡动力学方法所得到的结果基本一致. 而对于LC相体系, 拉伸模拟的前期(0～300 ps) ANP分子逐渐靠近单分子膜, 在约300 ps时ANP分子开始与膜表面接触, 在拉伸后期(300～600 ps) ANP分子在外力的作用下逐渐嵌入烷烃链区域. 然而在平衡动力学过程中, ANP分子并未进入烷烃链区域. 正是由于SMD方法能够模拟传统动力学方法难以实现的现象, 因此这一方法被广泛用于研究这些现象中的微观性质.

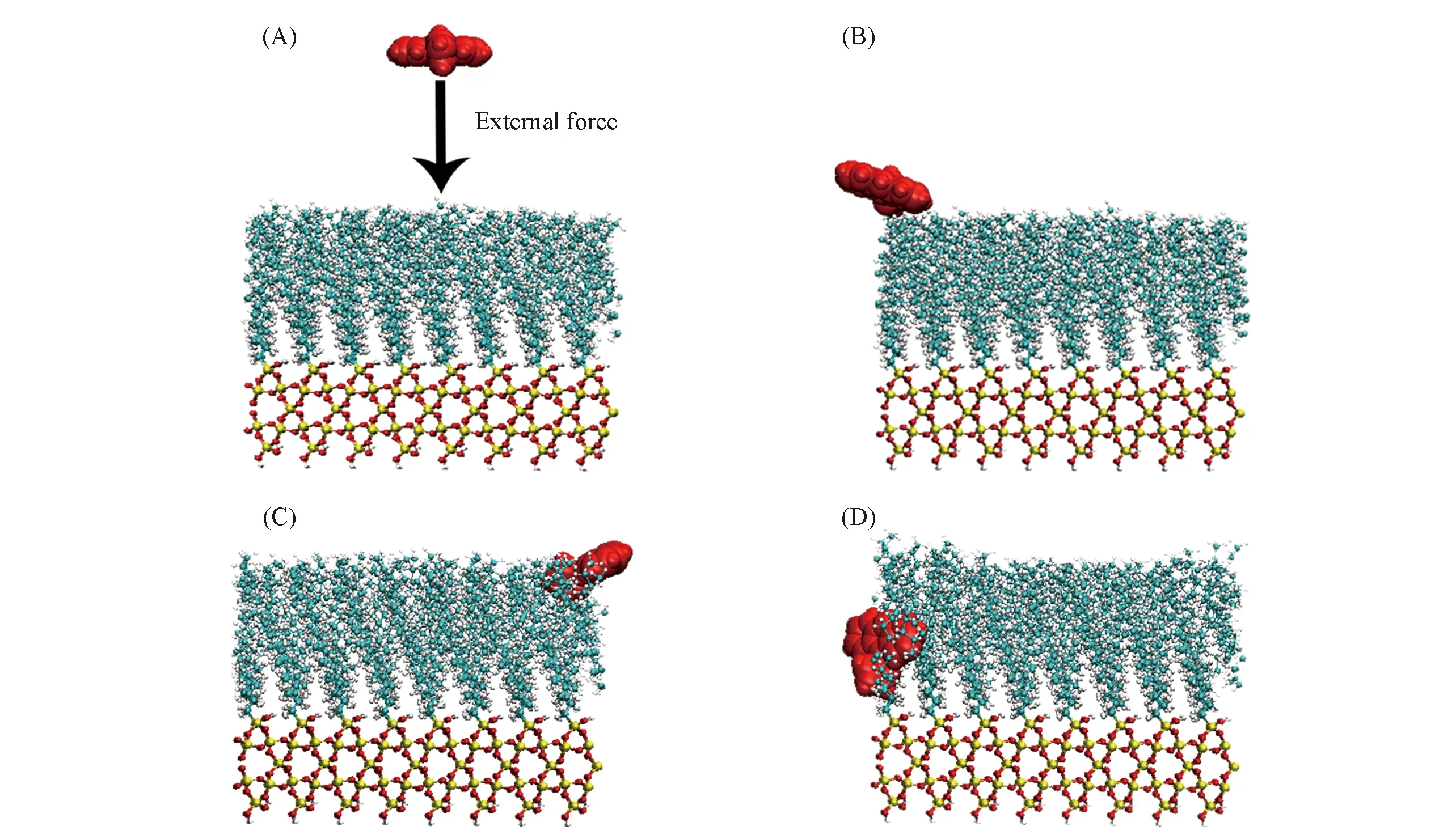
Fig.7 Configurations at different time during the SMD simulation for the LC systemTime/ps: (A) 0; (B) 300; (C) 460; (D) 600.

2.4 拉伸模拟过程中ANP分子所受弹簧拉力的分析

拉伸分子动力学模拟结合或分离过程是全原子的热力学运动过程, 这种过程是通过拉伸区域内原子间相互作用来消耗能量而体现的, 因此我们分析了这种非平衡运动过程中ANP分子受力情况的变化. 图8(A)为拉伸速度为0.005 nm/ps情况下, ANP分子沉积至LC相和LE相时所受弹簧拉力随模拟时间的变化图. 如上所述, ANP分子在这2种膜表面沉积过程的前期拉力值变化幅度不大, 因为前期这一过程中ANP分子是从气相中逐渐靠近烷烃链分子层膜表面, 并未受到任何阻碍. 而当ANP分子开始进入烷烃链分子层膜中时, 这2种自组装膜中ANP分子受力值均开始出现较大波动. 从图8(A)可见, ANP分子进入LC相烷烃链膜后, 受力变化比在LE相中更为明显.

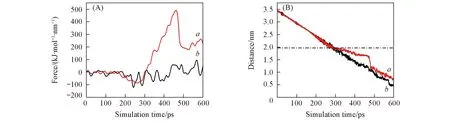
Fig.8 Time profiles of the external force applied on ANP(A) and time profiles of the vertical distance between COM of ANP molecule and the SiO2 surface(B)a. LC phase; b. LE phase. (B) The dashed line shows the surface of LC monolayer.

结合ANP分子在垂直自组装膜表面方向上距离的变化[图8(B)], 发现大约200 ps时ANP分子距离SiO2基底表面约2.0 nm, 也就是沉积在了LC相表面. 而之后由于受到排列较为致密的烷烃链阻碍, ANP分子的嵌入速度明显降低. 相应地, 弹簧拉力急剧增加以克服烷烃链对小分子的阻碍. 直到大约460 ps时拉力达到最大值, ANP分子才开始在外力作用下进入LC相烷烃链内部区域. 此时, 距离的变化出现突变, 这是由于外力作用使得烷烃链分子闪开缝隙以使小分子进一步深入. 而对于LE相, ANP分子虽然也会受到一定阻力, 只是阻力比LC相体系阻力小得多. 总之, 基底表面烷烃链的密度大小会影响ANP分子的沉积, 随着烷烃链密度的增大, ANP分子所受阻力增大, 因此难以进入烷烃链内部区域.

2.5 ANP分子沉积过程的均力势(PMF)

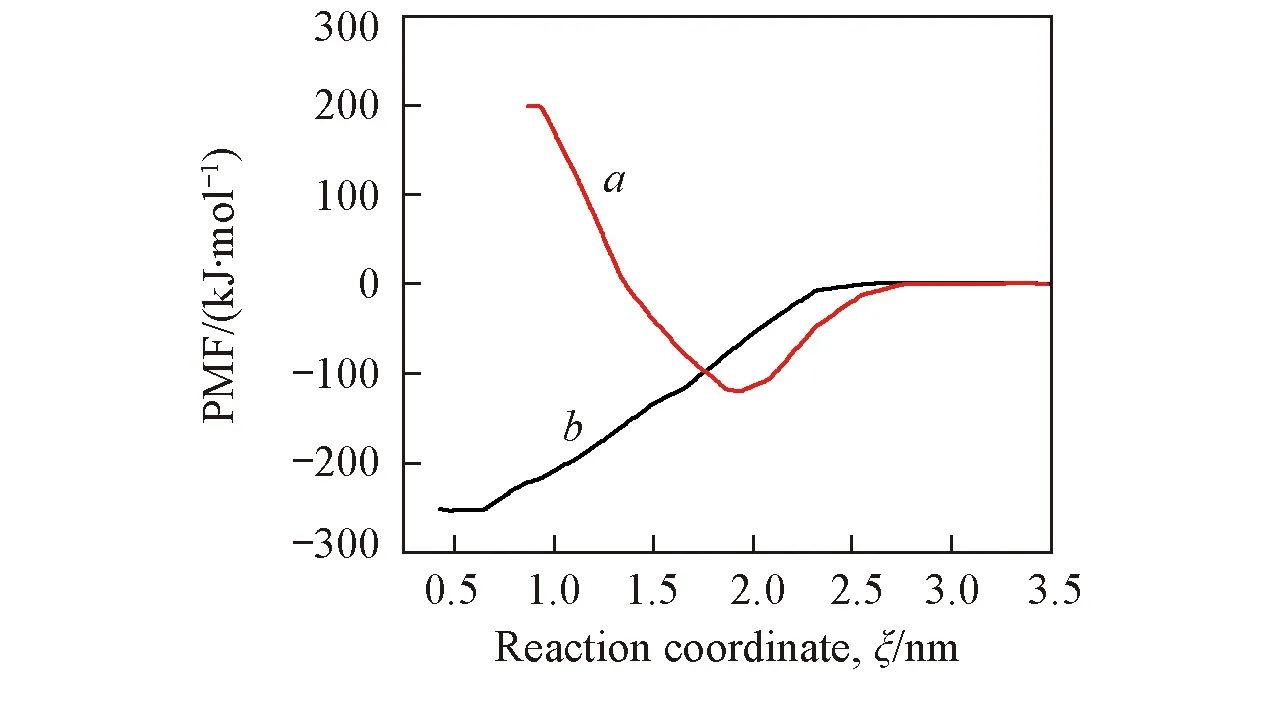
Fig.9 Potential of mean force along the reaction coordinate for ANP molecules deposited onto each SAMa. LC phase; b. LE phase.

有机荧光分子与固体表面不同相之间的结合能不同是解释有机荧光分子选择性沉积的重要依据. 本文利用伞形取样法[20]和加权柱状图分析法(WHAM)[25]计算了ANP分子在不同密度的自组装膜上沉积过程中的结合自由能. 在拉伸分子动力学模拟过程中, ANP分子质心上施加外力使其逐渐被拉进SAM烷烃链区域. 以ANP分子质心与二氧化硅基底表面之间垂直距离(约3.5 nm)作为反应坐标, 通过GROMACS中的g_wham命令[29]计算对应于该反应坐标的均力势(PMF)曲线, 结果如图9所示. 对于LC相和LE相, PMF曲线的最小点分别出现在1.93和0.55 nm处. 这说明ANP分子与LC相和LE相的稳定结合位点分别距离二氧化硅基底表面1.93和 0.55 nm, 这与平衡分子动力学模拟得到的结果(图3)非常吻合. 为了验证该方法的准确性,我们同样获得了其它3种不同烷烃链排列方式的LE相吸附ANP分子的PMF曲线, 见图S3(见本文支持信息). 可以看出, PMF曲线趋势具有较好的一致性, 结合位点同样与相应平衡动力学模拟结果吻合. 由此可见, PMF曲线可以用来预测和解释小分子在自组装膜上的吸附位点.

通过PMF曲线得到ANP分子与这2种不同密度自组装膜的结合能ΔG, 可以发现, ANP分子与LE相的结合能(约为-250 kJ/mol)要高于其与LC之间的结合能(约-120 kJ/mol), 这说明ANP分子在LE相中结合更加稳定. 因为ANP分子进入了LE相烷烃链内部区域而被烷烃链分子包围, 烷烃链对于ANP分子有一定限制作用, 导致其结合较为稳定. 而ANP分子倾向于沉积在LC相的分子层膜表面, 周围受到较小的空间位阻, 因此结合较不稳定. 在LC相体系中, ANP分子靠近二氧化硅基底表面处, 能量曲线逐渐升高至约200 kJ/mol, 正的能量值反映了结合状态的不稳定. 尽管LC相中烷烃链之间可能存在一定的分子间隙, 但是由于ANP分子中吡唑环和蒽基环之间并不是稳定的平面结构, 因此ANP分子在外力的作用下强制进入排列致密的LC相中, 挤压烷烃链造成了构象重叠而导致了体系能量增大. 需要注意的是, 由于没有小分子沉积的能量测定报道, 而是推测能量差异来解释实验现象, 因而本文计算得到的能量值并没有实验数据与之对应. 但是通过上述结合能的分析可以定性地得出结论, 即低密度的LE相与ANP分子之间结合更为稳定, 使得ANP分子会优先沉积在LE相, 因此具有LE相和LC相交替排列结构的二氧化硅基底模板可以诱导有机小分子定位沉积.

3 结 论

采用平衡分子动力学和拉伸分子动力学模拟研究了3(5)-(9-蒽基)吡唑(ANP)分子在二氧化硅基底表面自组装膜上的选择性沉积. 平衡分子动力学模拟结果显示, 在LE相, ANP分子进入了烷烃链内部区域, 而在LC相, ANP分子只停留在膜的表面. 拉伸分子动力学模拟结果表明, SAM表面烷烃链的密度大小会影响小分子在其表面的沉积, 烷烃链密度越大, ANP分子受到的阻力越大, 越难进入SAM烷烃链区域. 通过伞形取样法和加权柱状图分析法(WHAM), 得到了ANP分子在LC和LE相沉积过程的均力势(PMF). 结果表明ANP分子与LE相结合更为稳定, 因而ANP分子会优先沉积在LE相中. 本文从能量的角度解释了ANP分子在LC和LE相交替排列的二氧化硅模板上选择性沉积的机制.

感谢山东大学胶体与界面重点实验室苑世领教授对拉伸模拟计算的讨论和建议.

支持信息见http://www.cjcu.jlu.edu.cn/CN/10.7503/cjcu20150781.

[1] Gaal M., Gadermaier C., Plank H., Moderegger E., Pogantsch A., Leising G., List E., Adv. Mater., 2003, 15(14), 1165—1167

[2] Koide Y., Wang Q., Cui J., Benson D. D., Marks T. J., J. Am. Chem. Soc., 2000, 122(45), 11266—11267

[3] Cheek B. J., Steel A. B., Torres M. P., Yu Y., Yang H., Anal. Chem., 2001, 73(24), 5777—5783

[4] Lingerfelt B. M., Mattoussi H., Goldman E. R., Mauro J. M., Anderson G. P., Anal. Chem., 2003, 75(16), 4043—4049

[5] Hao J., Lu N., Wu Q., Hu W., Chen X., Zhang H., Wu Y., Wang Y., Chi L. F., Langmuir, 2008, 24(10), 5315—5318

[6] Hirtz M., Fuchs H., Chi L. F., J. Phys. Chem. B, 2008, 112(3), 824—827

[7] Chen X. D., Rogach A. L., Talapin D. V., Fuchs H., Chi L. F., J. Am. Chem. Soc., 2006, 128(30), 9592—9593

[8] Hao J., Lu N., Li L., Hirtz M., Gao L., Wang W., Du C., Fuchs H., Chi L. F., Soft Matter, 2010, 6(21), 5302—5304

[9] Gao L., Lu N., Hao J., Hu W., Shi G., Wang Y., Chi L. F., Langmuir, 2009, 25(6), 3894—3897

[10] Gleiche M., Chi L. F., Fuchs H., Nature, 2000, 403(6766), 173—175

[11] Gleiche M., Chi L. F., Gedig E., Fuchs H., Chem.Phys.Chem, 2001, 2(3), 187—191

[12] Choi J. M., Jeong S. H., Hwang D. K., Im S., Lee B. H., Sung M. M., Org. Electron., 2009, 10(1), 199—204

[13] Steudel S., Janssen D., Verlaak S., Genoe J., Heremans P., Appl. Phys. Lett., 2004, 85(23), 5550—5552

[14] Hirtz M., Kumar N., Franke J. H., Hao J., Lu N., Fuchs H., Chi L. F., J. Colloid Interf. Sci., 2013, 389(1), 206—212

[15] Xu Z., Hirtz M., Yuan S. L., Liu C. B., Chi L. F., Chem. Phys. Lett., 2011, 507(1—3), 138—143

[16] Zhang C., Xu Z., Yan H., Gao F., Yuan S. L., Chem. Phys. Lett., 2013, 571, 38—43

[17] Zhang C., Du C., Yan H., Yuan S. L., Chi L. F., RSC Adv., 2013, 3(35), 15404—15410

[18] Shevade A. V., Zhou J., Zin M. T., Jiang S. Y., Langmuir, 2001, 17(24), 7566—7572

[19] Izrailec S., Stepaniants S., Isralewitz B., Kosztin D., Lu H., Molnar F., Wriggers W., Schulten K., Steered Molecular Dynamics, Springer-Verlag, Berlin, 1998

[20] Torrie G. M., Valleau J. P., J. Comput. Phys., 1977, 23(2), 187—199

[21] He Z. J., Zhou J., Acta Chim. Sinica, 2011, 69(24), 2901—2907(贺仲金, 周健. 化学学报, 2011, 69(24), 2901—2907)

[22] He J., Feng X. Z., Shao G. X., Cai W. S., Chem. J. Universities Chinese, 2015, 36(1), 110—115(何佳, 冯喜增, 邵学广, 蔡文生. 高等学校化学学报, 2015, 36(1), 110—115)

[23] Zhang J. L., Zheng Q. C., Zhang H. X., J. Phys. Chem. B, 2010, 114(21), 7383—7390

[24] Sun W. Q., Zhang J. L., Zheng Q. C., Sun Z. W., Zhang H. X., Acta Phys. Chim. Sinica, 2013, 29(4), 843—848(孙维琦, 张继龙, 郑清川, 孙志伟, 张红星. 物理化学学报, 2013, 29(4), 843—848)

[25] Kumbia S., Bouzida D., Swendsen R. H., Kollman P. A., Rosenberg J. M., J. Comput. Chem., 1992, 13(8), 1011—1021

[26] Hozumi A., Asakura S., Fuwa A., Shirahata N., Kameyama T., Langmuir, 2005, 21(18), 8234—8242

[27] Janssen D., DePalma R., Verlaak S., Heremans P., Dehaen W., Thin Solid Films, 2006, 515(4), 1433—1438

[28] Jorgensen W. L., Maxwell D. S., Tirada-Rives J., J. Am. Chem. Soc., 1996, 118(45), 11225—11236

[29] Hess B., Kutzner C., van der Spoel D., Lindahl E., J. Chem. Theory Comp., 2008, 4(3), 435—477

[30] Schmidt M. W., Baldridge K. K., Boatz J. A., Elbert S. T., Gordon M. S., Jensen J. H., Koseki S., Matsunaga N., Nguyen K. A., Su S. J., Windus T. L., Dupuis M., Montgomery J. A., J. Comput. Chem., 1993, 14(11), 1347—1363

[31] Lorenz C. D., Webb III E. B., Stevens M. J., Chandross M., Grest G. S., Tribol. Lett., 2005, 19(2), 93—98

[32] Berendsen H. J. C., Postma J. P. M., van Gunsteren W. F., DiNola A., Haak J. R., J. Chem. Phys., 1984, 81(8), 3684—3690

[33] Hess B., Bekker H., Berendsen H. J. C., Fraaije J. G. E. M., J. Comput. Chem., 1997, 18(12), 1463—1472

[34] Essman U., Perera L., Berkowitz M. L., Darden T., Lee H., Pedersen L. G., J. Chem. Phys., 1995, 103(19), 8577—8593

[35] Humphrey W., Dalke A., Schulten K., J. Mol. Graph. Model., 1996, 14(1), 33—38

(Ed.: Y, Z)

Molecular Dynamics Studies on the Selective Deposition of 3(5)-(9-Anthryl) Pyrazole onto Self-assembled Monolayers†

ZHANG Luge1, XUE Zexu1, ZHANG Chong1*, YAN Hui2*

(1. School of Chemistry and Chemical Engineering, 2. School of Pharmacy, Liaocheng University, Liaocheng 252059, China)

The site-selective deposition behavior of 3(5)-(9-anthryl) pyrazole(ANP) onto self-assembled monolayers(SAMs) patterned substrate was studied via the equilibrium and steered molecular dynamics methods. Two kinds of different densely packed SAMs were constructed on silicon oxide substrates as the patterned templates, which represent liquid expanded(LE) and liquid condensed(LC) phases. Equilibrium molecular dynamics(MD) simulations showed that the packing density of alkyl chains on the substrate could influence the deposition behavior of the ANP molecules. On the LE covered SAM, the small molecule would submerge deeply into the alkyl chains film, while ANP molecule would deposit on the surface of LC film. Steered molecular dynamics showed that ANP molecule was hindered from the densely packed LC film. However, there was less hindrance for ANP to submerge into the LE film. Using umbrella sampling and the weighted histogram analysis method, the potential of mean force(PMF) of the deposition process of ANP onto the two patterned templates was calculated. From the PMF curves, the favorite deposition location of ANP onto the two SAMs was determined, which agreed well with that obtained from equilibrium MD simulations. The binding energies between ANP and the two SAMs can be estimated based on PMF, which could be used to explain the site-selective deposition of ANP on different densely packed SAMs.

Self-assembled monolayers(SAM); Site-selective deposition; Steered molecular dynamics; Umbrella sampling; 3(5)-(9-Anthryl)pyrazole; Low intensity liquid expanded phase; High intensity liquid condensed phase; Potential of mean force

10.7503/cjcu20150781

2015-10-10.

日期: 2016-01-24.

国家自然科学基金(批准号: 21203084)和山东省自然科学基金(批准号: 13LB21)资助.

O641

A

联系人简介：延 辉, 男, 博士, 讲师, 主要从事固体表面吸附的模拟研究. E-mail: yanhuilcu@163.com

张 翀, 男, 博士, 副教授, 主要从事量子化学的理论研究. E-mail: zhangchong@lcu.edu.cn

† Supported by the National Natural Science Foundation of China(No.21203084) and the Shandong Provincial Natural Science Foundation, China(No.13LB21).