一维铁磁海森堡模型的热力学性质
陈 渊, 尹送求
(广州大学物理与电子工程学院, 广州 510006)
一维铁磁海森堡模型的热力学性质
陈 渊*, 尹送求
(广州大学物理与电子工程学院, 广州 510006)
利用修正的自旋波理论研究有次近邻相互作用的一维自旋为1/2的铁磁海森堡模型. 通过自洽方法,得到次近邻相互作用对系统的热力学性质的影响. 结果表明,当存在次近邻相互作用时,体系比热的最大值及其对应位置分别是温度的指数和线性函数关系. 当比热取最大值时,磁化率、内能及自由能均为次近邻相互作用的递减线性函数. 而熵是次近邻相互作用的递减指数函数. 在不存在次近邻相互作用时,其结果与Bethe Ansatz精确解相符合.
海森堡模型; 自旋波理论; 次近邻相互作用
标准的自旋波理论[1-3]是解决低温海森堡铁磁模型热力学性质的强有力的方法,并且它推动了海森堡铁磁理论更深层次的研究和实验解释[4-9]. 然而当空间维度低于三维时,传统的自旋波理论在低温时,由于低维各项同性使铁磁系统[10]的长程有序缺失,从而导致热力学发散问题,因此,传统的自旋波理论无法给出热力学物理量的定量信息. 幸运地是,可以通过TAKAHASHI方法[11]:限制总磁化强度为0,修正传统的自旋波理论,解决此类热力学发散问题. TAKAHASHI利用该方法成功地得到了低维的低温热力学性质,并且其结果与Bethe Ansatz精确解相符合[11]. 该方法已经被广泛应用于各类低维磁性系统,如反铁磁体[12-13]、铁磁体[14-15]、阻挫磁体[7,16-17]、各向异性磁体[18-20]、自旋声子耦合系统[21]等.
近年来,磁场与热力学物理量的峰值函数关系引起了人们的极大关注,而这些函数关系已在低维海森堡铁磁模型中得到广泛研究,如实空间的重整化群理论[22]、精确有限晶格对角化方法[23]、格林函数方法[24-28]、Bethe Ansatz精确解方法[23]、量子蒙特卡洛方法[28]等. 这些研究显示,在弱磁场(磁场强度B较弱)时磁化率的最大值位置是磁场B的指数函数[22,24-25,28],而在强磁场时最大磁化率的位置却是B的线性函数[24,28]. 而磁化率的峰值在整个的磁场区域均为递减的指数函数[23-28]. 对于比热的最大值而言,在弱磁场时,比热的峰值及其位置都是B的递增函数关系[23,27]; 而在强磁场时,最大比热的位置显示线性递增函数关系[23-24,27],而比热峰值则是B的递减指数函数关系[27]. 此外,还发现在比热取最大值时,体系的内能也是B的线性递减函数[27].
对于不存在次近邻相互作用的情况已被TAKAHASHI研究[11]. 本文建立存在次近邻相互作用的一维海森堡铁磁模型. 实现TAKAHASHI方法的方案是通过建立一个理想的自旋波密度矩阵,使得自由能取极小值来计算低温热力学性质. 然而该方案计算复杂. 而本文提供另外一种思路:通过在哈密顿量中引入一个拉格朗日因子使得总的磁化强度为0,得到一组自洽方程,从而消除热力学发散问题. 基于修正的自旋波理论,在修正后的自旋波理论框架中,研究次近邻相互作用低温热力学性质的影响.
1 理论模型
在考虑次近邻相互作用下,一维铁磁海森堡磁链的哈密顿量可写为
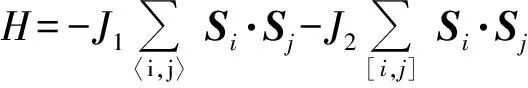
(1)
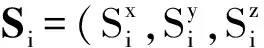
为了克服传统自旋波在一维情况下出现每格点的粒子占有数发散问题,引入TAKAHASHI方法[12],即限制总的磁化强度为0:
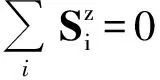
(2)
为了强化约束方程(2),在哈密顿量中引入拉格朗日因子μ,则体系的有效哈密顿量可改为:
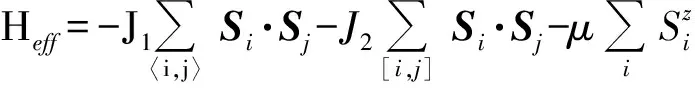
(3)
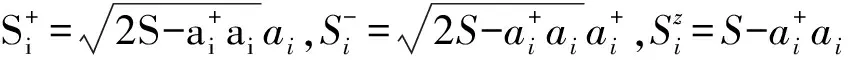
(4)
保留(3)展开式中的双线性项,哈密顿量近似为:
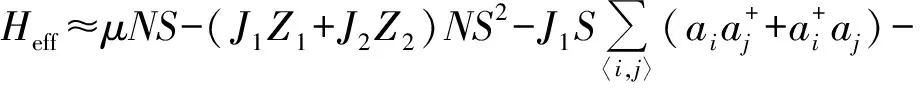
(5)
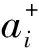
利用傅立叶变换:
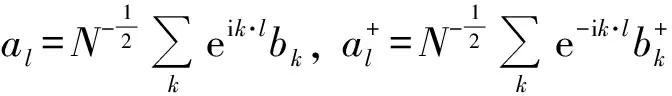
(6)
可得
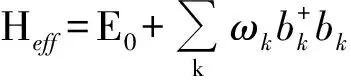
(7)
其中
E0=-μN-(J1Z1+J2Z2)NS2,
(8)
ωk=μ+2J1SZ1(1-γ1k)+2J2SZ2(1-γ2k),
(9)
其中γ1k和γ2k分别表示最近邻和次近邻的结构因子数,并且满足
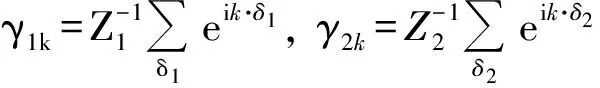
(10)
其中,Z1和Z2分别表示最近邻和次近邻的配位数,在一维情况下,Z1=Z2=2,γ1k=cosk,γ2k=cos(2k).
考虑到波色爱因斯坦分布函数,
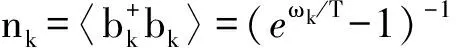
(11)
并将式(11)代入方程(2)中,可得到体系的自洽方程
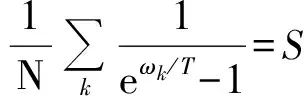
(12)
其中,T表示温度,拉格朗日因子便可以通过自洽方程(12)确定,求得μ,便可研究体系的热力学性质.
2 结果与讨论
次近邻相互作用将影响体系(如内能、比热、磁化率、熵及自由能等)的热力学性质,由于本文采用自然单位制,自由能、内能和拉格朗日因子的单位均为开尔文,即K;磁化率的单位为K-1; 而熵和比热均无量纲. 本文的调控参数α=J2/J1,为了简化计算,令J1和S均为1/2,且配位数Z1=Z2=2.
要获得体系物理量的热力学性质,首先要确定拉格朗日因子的值. 利用自洽方程(12)得到拉格朗日因子μ与温度T的函数关系(图1). 对于给定的α,μ随T的升高而增大. 然而对于确定的T时,α越大,μ反而越小.
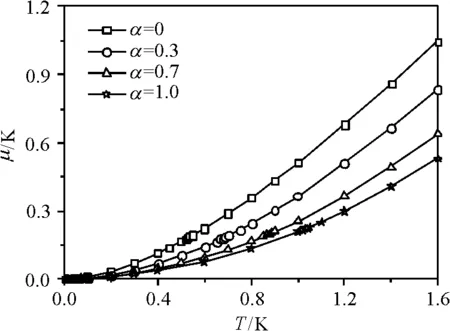
图1 拉格朗日因子μ与温度的关系
Figure 1 Lagrange multiplierμas a function of the temperature
2.1 内能、熵和自由能
在求出拉格朗日因子后,即可研究体系的热力学性质. 首先考虑体系每个格点的内能U=〈Heff〉/N,即
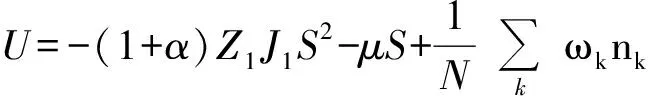
(13)
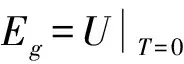
Eg=-0.25-0.25α.
(14)
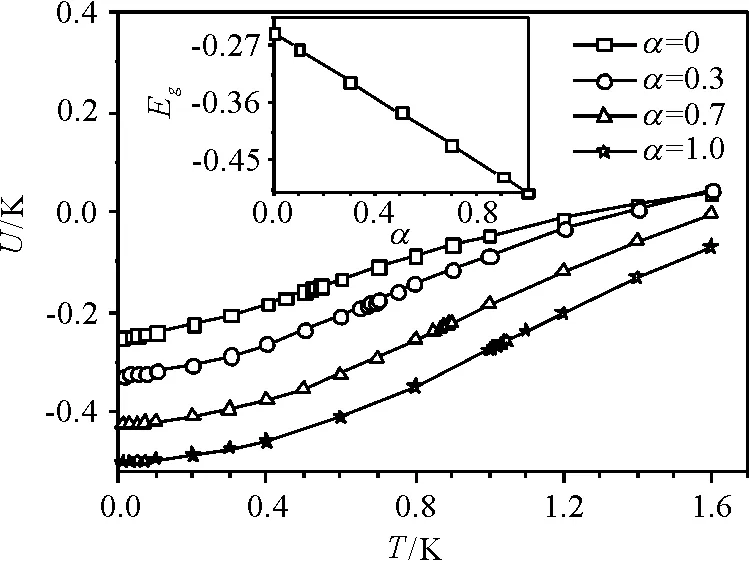
图2 每个格点内能与温度的关系
当α=0时,计算每个格点的基态能为-0.25,这与通过Bethe Ansatz精确解方法[30]得到的-0.251 1接近,但是优于利用重整化群方法[31]得到的结果(-0.240 1).
如前文所述,nk是波色爱因斯坦分布函数. 利用分布函数,可得系统的熵和自由能,即
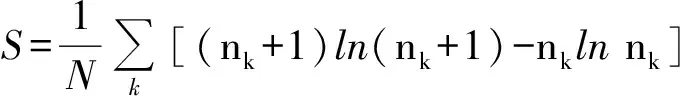
(15)
F=U-TS.
(16)
通过式(15)和式(16)作出熵和自由能与温度的关系(图3). 熵是温度的递增函数,但熵又随着α的增大而减少. 对于自由能而言,自由能却是温度的递减函数,并且对于低温时,自由能随着α的增大而减少,然而超过一定温度时,自由能又是α的递增函数.
2.2 磁化率
〉.
(17)
由于方程(1)没有考虑磁场的作用,体系有自旋对称性,导致在x、y、z方向的自旋关联函数为:
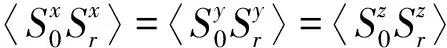
(18)
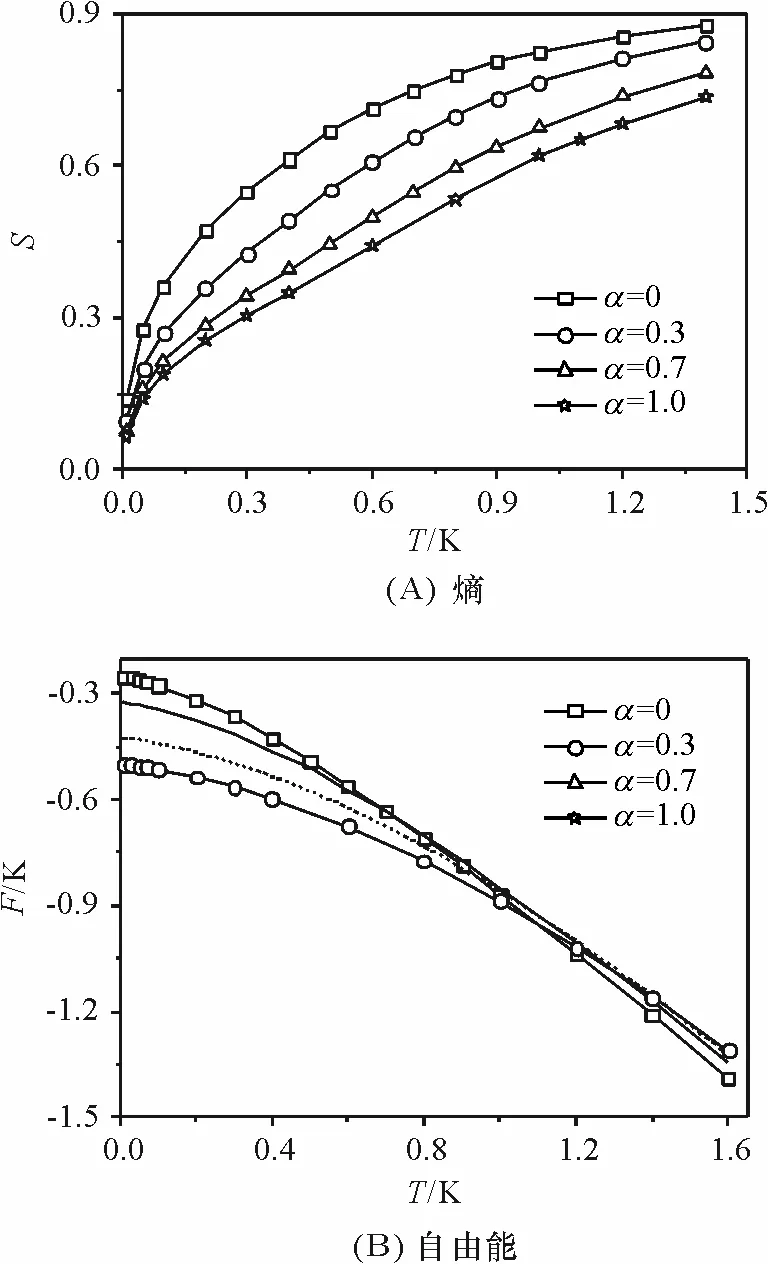
图3 熵和自由能与温度的关系
Figure 3 The temperature dependence of the entropy and the free energy
因此均匀磁化率为:
〉.
(19)
借助Holstein-Primakoff变换及Fourier变换,式(19)可表示为:
).
(20)
由于方程(20)由nk波色爱因斯坦分布函数给出,因此方程(20)可用波色-爱因斯坦积分函数表示[11]:
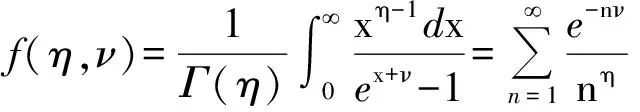
(21)
而方程(21)在ν=0且η为非正整数时,可展开[32]:
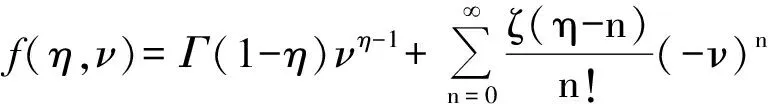
(22)
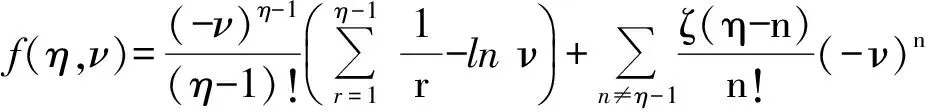
(23)
其中,Γ(η)和ζ(η)分别表示Gamma函数和Riemann’szeta函数.
当温度很低时,由方程(12)、(19)可以得到拉格朗日因子μ和磁化率的表达式:
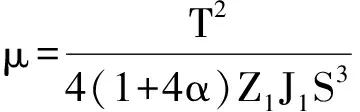
(24)
.
(25)
由式(25)可知,低温下,磁化率与温度有负指数关系,则定义磁化率系数为T2. 表1为当T→0时次近邻相互作用参数α对磁化率系数的影响. 磁化率系数T2随着α的增大而增大,并且对于无相互作用时,根据自洽方程得到的零温结果为1/24,这与通过理想自旋波密度方法[11]得到的结果一样,并且与BetheAnsatz精确解方法[33]得到的0.041 675、格林函数方法[24-28]、量子蒙特卡洛方法[28]得到的结果0.041 667很好符合.
表1 温度趋于零时磁化率系数T2的值
Table 1 Values of the susceptibility coefficient limT→0 T2in the zero temperature limit
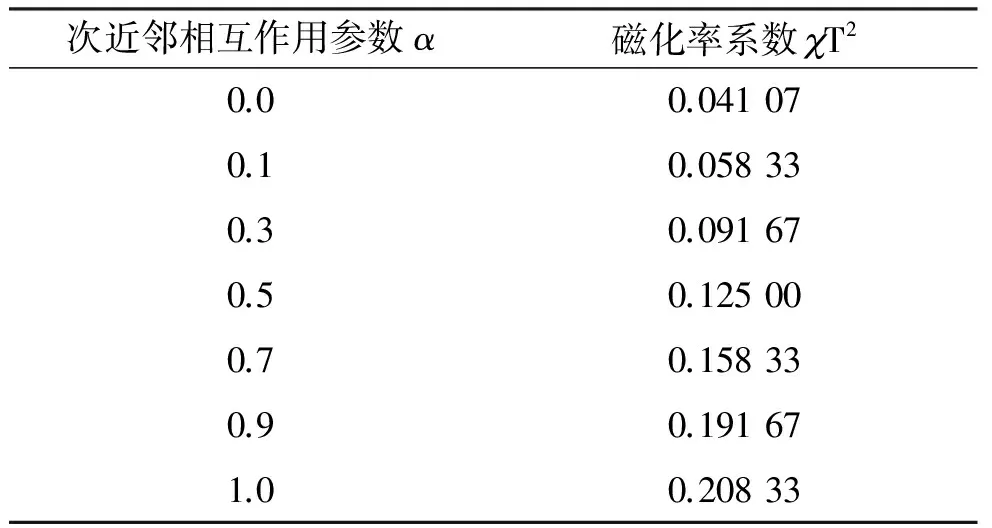
表1 温度趋于零时磁化率系数T2的值
次近邻相互作用参数α磁化率系数 T20.00.041070.10.058330.30.091670.50.125000.70.158330.90.191671.00.20833
2.3 比热
为了研究次近邻对系统比热C=∂U/∂T的影响,方程(13)两边同时对温度T求导可得:
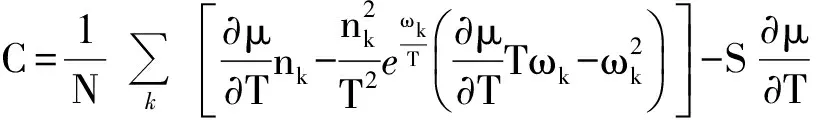
(26)
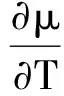
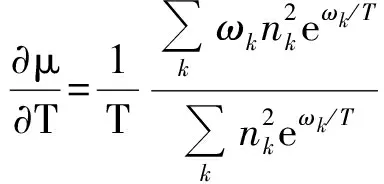
(27)
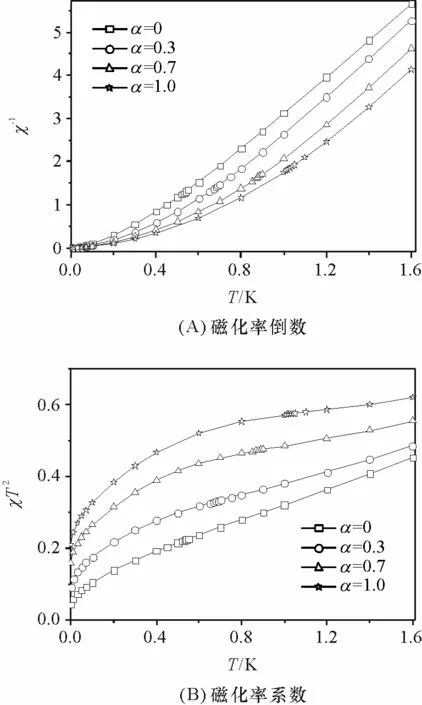
图4 磁化率倒数和磁化率系数与温度的关系
Figure 4 Temperature dependences of the inverse susceptibility and the susceptibility coefficient
在低温时,由方程(20)~(22)的自旋波计算比热:
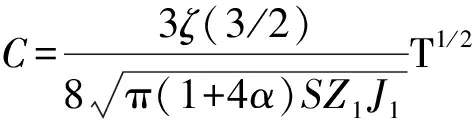
(28)
从方程(28)可知,低温时,比热正比于T1/2, 类比磁化率系数的定义,可以定义比热系数为C/T1/2. 在温度趋于0时,比热系数C/T1/2的值如表2所示. 与磁化率系数不同的是:比热系数C/T1/2随着α的增大而减少. 当无相互作用时,得到的比热系数极限值为0.781 64与由理想自旋波密度方法[11]得到的结果一致,并且与通过Bethe Ansatz精确解方法[33]得到的值0.781 5符合得很好.
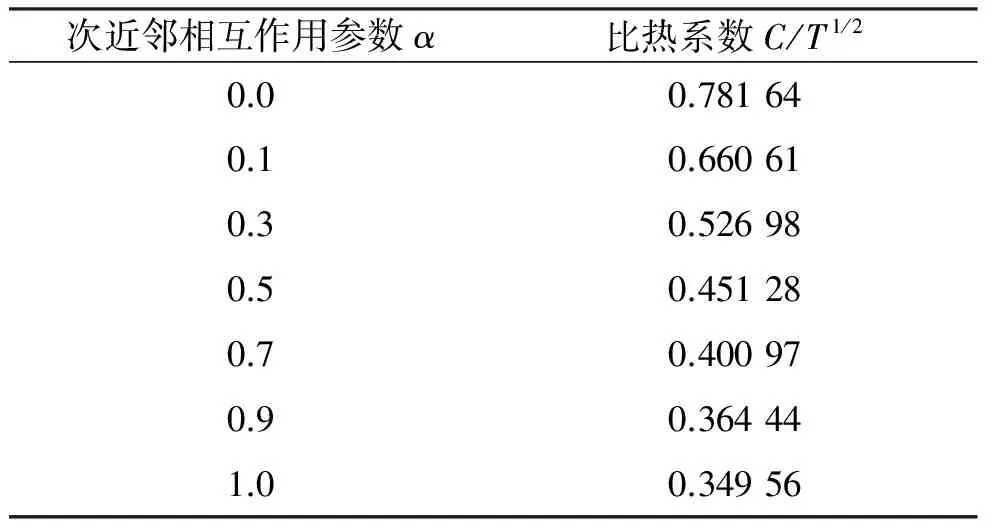
表2 T→0时比热系数C/T 1/2的极限
在有限温度区域,由方程(26)给出比热及比热系数,其图像如图5所示. 比热C从0开始增大,当达到T=Tmax时,比热达到最大值,随后开始递减,并且比热C的峰值随α的增大而变大. 图5A内插图显示,在无相互作用时,比热与Bethe Ansatz精确解方法(BA)[33]及精确有限晶格对角化方法(ED)[23]得到的结果接近,并且在温度低于0.15 K时,所得结果优于格林函数方法(GFM)[28]. 由图5B可知,当α<0.05时,比热系数C/T1/2是温度T的单调递减函数,然而当α>0.05时,C/T1/2呈现先递减、后递增、再递减趋势. 由图5B内插图可以看出,比热系数的最大值即(C/T1/2)max出现在α=0.30附近.

图5 比热和比热系数与温度的关系
Figure 5 Temperature dependences of the specific heatCand the specific heat coefficient
图6为比热峰值及其峰位置与次近邻相互作用参数α之间的关系,比热峰值与α成正指数关系,这与有磁场作用时一维[23,28](或者二维[27])比热峰值的规律不同. 峰值的位置与α成正线性关系,而这又与有强磁场作用时[23,25,27]有相似的规律.比热峰值及峰位置与α的关系式近似为:

(29)
Tmax=0.494 56α+0.531 30.
(30)
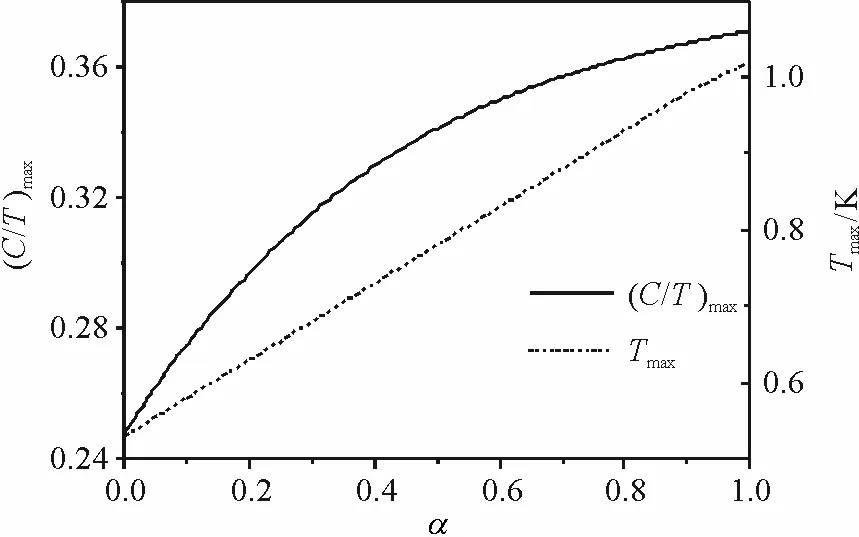
图6 比热的峰值和峰位置与α的关系
Figure 6 Height and position of the specific heat maximum as a function ofα
2.4 比热最大值时的磁化率、内能、自由能、熵
当比热取最大值时,将对应的Tmax代入磁化率(Tmax)、内能U(Tmax)、自由能F(Tmax)及熵S(Tmax)的表达式中,研究次近邻对体系的这些物理量的影响(图7和图8),结果表明,此时的磁化率、内能、自由能均是α的线性递减函数. 这些规律与存在磁场作用时磁场对体系内能具有类似线性规律[27]. 而由图8可知,熵却是α的递减指数函数,并且可近似为:
(Tmax)=-0.244 17α+0.786 19,
(31)
U(Tmax)=-0.115 74α-0.147 98,
(32)
F(Tmax)=-0.393 05α-0.506 81,
(33)
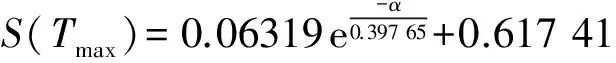
(34)
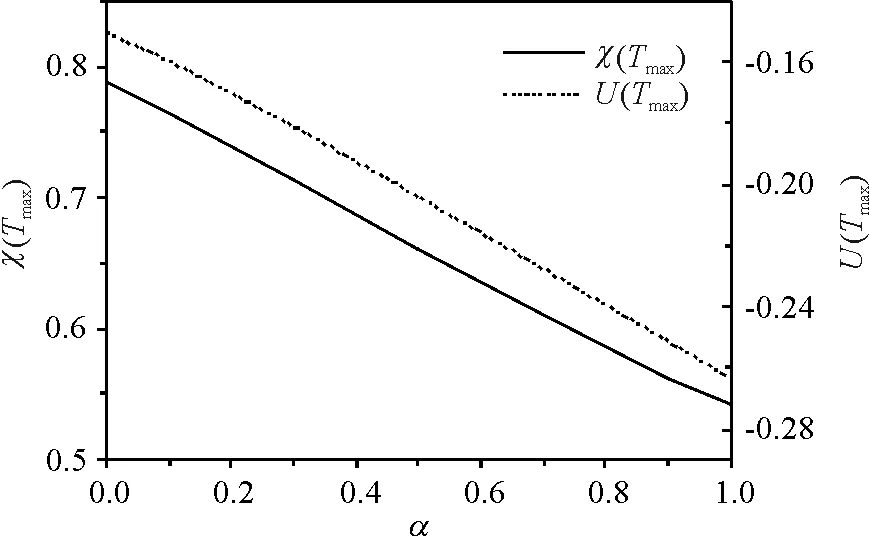
图7 当比热在峰值位置时磁化率和内能与α的关系
Figure 7 Susceptibility and internal energy as a function ofαatC(Tmax)
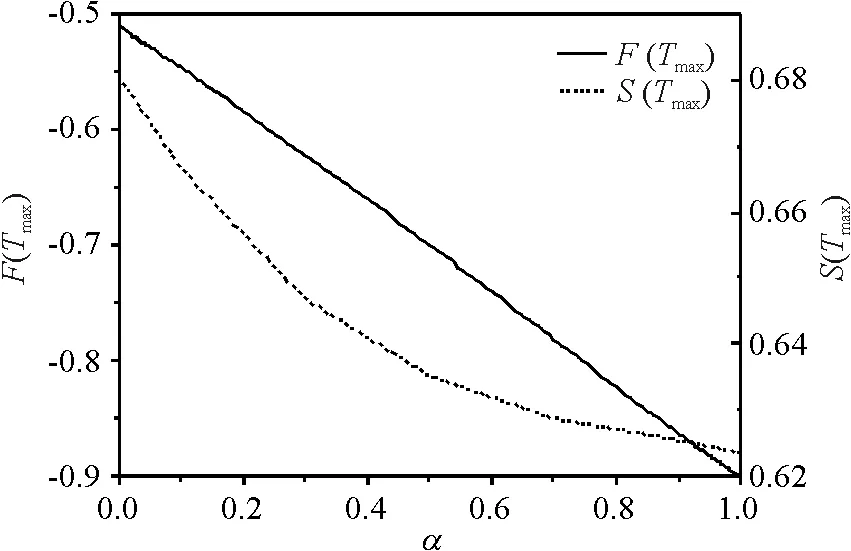
图8 当比热在峰值位置时自由能和熵与α的关系
Figure 8 Free energy and entropy as a function ofαatC(Tmax)
3 结论
利用TAKAHASHI的方法即限制总磁化强度为0,得到了有次近邻相互作用的铁磁海森堡链的修正自旋波理论. 研究表明,次近邻相互作用J2对体系的低温热力学性质有很大的影响,且在低温时,均匀的磁化率、内能U、熵S及自由能F都是J2的递减函数,但是对于高温区域,自由能F则会随着J2的增大而增大. 对于无次近邻相互作用时,该结果与BetheAnsatz精确解方法得到的结果一致.
然而对于次近邻相互作用较大时,J2会阻碍T2的增加. 在有限温度区域,对于α<0.05时,比热C及比热系数C/T1/2均显现一种最大值的行为,比热C随着温度的增加趋于最大值,并且随着α的增大,其相应的比热C的峰值也变大,幅宽也变宽. 由J2引起比热C最大值的位置变化线性关系与已有高磁场得到的结果相似. 当比热取最大值时,内能、磁化率及自由能都随着次近邻相互作用加强而成负线性关系,但熵与其成指数关系. 在0≤α≤1区域,比热C最大值近似服从指数关系,该规律和有磁场存在时得到的最大比热规律有很大的区别. 该研究为后续铁磁材料的相关热力学性质的研究提供了基础.
[1]ANDERSONPW.Anapproximatequantumtheoryoftheantiferromagneticgroundstate[J].PhysicalReview,1952,86(5):694-701.
[2]KUBOR.Thespin-wavetheoryofantiferromagnetics[J].PhysicalReview,1952,87(4):568-580.
[3]OGUCHIT.Theoryofspin-waveinteractionsinferro-andantiferromagnetism[J].PhysicalReview,1960,117(1):117-123.
[4]KREISELA,PERTERM,KOPIETZP.Singularspin-wavetheoryandscatteringcontinuaintheconestateofCs2CuCl4[J].PhysicalReviewB,2014,90(7):Art07513,12pp.
[5]ISHIZUKAHIROAKI,BALENTSLEON.Magnetisminspin-1/2doubleperovskiteswithstrongspin-orbitinteractions[J].PhysicalReviewB,2014,90(18):Art184422,16pp.
[6]CORREGGIM,GIULIANIA,SEIRINGERR.Validityofspin-wavetheoryforthequantumHeisenbergmodel[J].EurophysicsLetters,2014,108(2):Art20003,5pp.
[7]LAFLORENCIEN,LUITZDJ,ALETF.Spin-waveapproachforentanglemententropiesoftheJ1-J2Heisenbergantiferromagnetonthesquarelattic[J].PhysicalReviewB,2015,92(11):Art115126,14pp.
[8]TOTHS,LAKEB.Linearspinwavetheoryforsingle-Qincommensuratemagneticstructures[J].JournalofPhysics:CondensedMatter,2015,27(16):Art166002,10pp.
[9]CHISNELLR,HELTONJS,FREEDMANDE,etal.Topologicalmagnonbandsinakagomelatticeferromagnet[J].PhysicalReviewLetters,2015,115(14):Art147201,5pp. [10]MERMINND,WAGNERH.Absenceofferromagnetismorantiferromagnetisminone-ortwo-dimensionalisotropicHeisenbergmodels[J].PhysicalReviewLetters,1966,17(22):1133-1136.[11]TAKAHASHIM.Few-dimensionalHeisenbergferromagnetsatlowtemperature[J].PhysicalReviewLetters,1987,58(2):168-170.
[12]TAKAHASHIM.Modifiedspin-wavetheoryofasquare-latticeantiferromagnet[J].PhysicalReviewB,1989,40(4):2494-2501.
[13]HIRSCHJE,TANGS.Spin-wavetheoryofthequantumantiferromagnetwithunbrokensublatticesymmetry[J].PhysicalReviewB,1989,40(7):4769-4772.
[14]YAMAMOTOS,FUKUIT.ThermodynamicpropertiesofHeisenbergferrimagneticspinchains:ferromagneticandantiferromagneticcrossover[J].PhysicalReviewB,1998,57(12):R14008-R14011.
[15]YAMAMOTOS.Bosonicrepresentationofone-dimensionalHeisenbergferrimagnets[J].PhysicalReviewB,2004,69(6):Art064426,9pp.
[16]KARCHEVN.FerromagnetismofMnV2O4spinel[J].JournalofPhysics:CondensedMatter,2009,21(5):Art056008,5pp.
[17]SONGHF,LAFLORENCIEN,RACHELS,etal.Entanglemententropyofthetwo-dimensionalHeisenbergantiferromagnet[J].PhysicalReviewB,2011,83(22):Art224410,7pp.
[18]CASTROEV,PERESNMR,BEACHKSD,etal.Sitedilutionofquantumspinsinthehoneycomblattice[J].PhysicalReviewB,2006,73(5):Art54422,17pp.
[19]HAUKEP,ROSCILDET,MURGV,etal.Modifiedspin-wavetheorywithorderingvectoroptimization:frustratedbosonsonthespatiallyanisotropictriangularlattice[J].NewJournalofPhysics,2010,12(5):Art053036,33pp.
[20]LIAOL,CHENY.Spin-wavetheoryappliedtothelow-temperaturepropertiesofthespin-1/2ferromagneticchainwithy-directionexchangeanisotropy[J].SuperlatticesMicrostruct,2014,5(16):82-97.
[21]GOUVAME,PIRESAST.Effectofspin-phononcouplingonthehaldanegapinantiferromagneticHeisenbergchains[J].PhysicalReviewB,2007,75(5):Art052401,4pp.[22]SZNAJDJ.Fielddependenceofthesusceptibilitymaximumtemperatureinferromagnets[J].PhysicalReviewB,2001,64(5):Art052401,4pp.
[23]JUNGERI,IHLED,RICHERJ,etal.Green-functiontheoryoftheHeisenbergferromagnetinamagneticfield[J].PhysicalReviewB,2004,70(10):Art104419,8pp.
[24]HUAY,CHENY,PENGLJ.TheanisotropicHeisenbergferromagnetinamagneticfield[J].JournalofMagnetismandMagneticMaterials,2007,313(2):366-372.
[25]ANTSYGINATN,POLTAVSKAYAMI,POLTAVSKYII,etal.Thermodynamicsoflow-dimensionalspin-1/2Heisenbergferromagnetsinanexternalmagneticfieldwithinagreenfunctionformalism[J].PhysicalReviewB,2008,77(2):Art024407,10pp.
[26]HRTELM,RICHATERJ,IHLED.Thermodynamicsofthefrustratedone-dimensionalspin-1/2Heisenbergferromagnetinamagneticfield[J].PhysicalReviewB,2011,83(21):Art214412,8pp.
[27]PUQ,CHENY.Thefield-inducedlawsofthermodynamicpropertiesintwo-dimensionalspin-1ferromagneticHeisenbergmodelwiththeexchangeandsingle-ionanisotropies[J].PhysicaB,2013,410:74-80.
[28]JUHSZI,JUNGERS,IHLED,etal.ThermodynamicsofHeisenbergferromagnetswitharbitraryspininamagneticfield[J].PhysicalReviewB,2008,77(17):Art174411,15pp.
[29]HOLSTEINH,PRIMAKOFFH.Fielddependenceoftheintrinsicdomainmagnetizationofaferromagnet[J].Phy-sicalReview,1940,58(12):1098-1113.
[30]TAKAHASHMI.Numericalcalculationofthermodynamicquantitiesofspin-1/2anisotropyHeisenbergring[J].ProgressTheoreticalPhysics,1974,51(5):1348-1354.
[31]LANGARIA.PhasediagramoftheantiferromagneticXXZmodelinthepresenceofanexternalmagneticfield[J].PhysicalReviewB,1998,58(21):14467-14475.
[32]ROBINSONJE.NoteonBose-Einsteinintegralfunctions[J].PhysicalReview,1951,83(3):678-679.
[33]YAMADAM,TAKAHASHIM.Criticalbehaviorofspin-1/2one-dimensionalHeisenbergferromagnetatlowtemperatures[J].JournalofthePhysicalSocietyofJapan,1986,55(6):2024-2036.
【中文责编:成文 英文责编:肖菁】
Thermodynamic Properties of One-Dimensional Ferromagnetic Heisenberg Model
CHEN Yuan*, YIN Songqiu
(School of Physics and Electronic Engineering, Guangzhou University, Guangzhou 510006, China)
The modified spin-wave method is applied to the one-dimensional spin-1/2 ferromagnetic Heinsenberg model with next-nearest neighbor interaction. The influence of the next-nearest neighbor interaction on the thermodynamic properties of the system is obtained within the self-consistent method. The exponential and linear laws which are induced by next-nearest neighbor interaction are found for heights and positions of maximum of the specific heat, respectively. At positions of the specific heat maximum, the magnetic susceptibility, as well as the internal energy and free energy, exhibits the linear decrease with the next-nearest neighbor interaction. But the entropy has an exponential decrease. The results agree with the Bethe Ansatz data in the case without next-nearest neighbor interaction.
Heisenberg model; spin-wave method; next-nearest interaction
2016-05-12 《华南师范大学学报(自然科学版)》网址:http://journal.scnu.edu.cn/n
国家自然科学基金项目(10974059);广州市教育局科技项目(12A005S)
O41
A
1000-5463(2016)05-0008-07
*通讯作者:陈渊,教授,Email:newbayren@163.com.

