电场背景下手征相变的临界线

陈建兴， 魏 颖， 常晓婷， 张肖阳

(辽宁师范大学 物理与电子技术学院，辽宁 大连 116029)

1 NJL模型

本文采用具有三个味道的NJL模型，夸克场定义为ψ=(u,d,s)T，其拉格朗日密度如下：

(1)

其中，在协变导数Dμ=∂μ-iQAμ中引入了电磁势Aμ，取Aμ=(-Ex3,0,0,0)，得到沿z方向的匀强电场.Q=diag(2e/3,-e/3,-e/3)是夸克的电荷矩阵，流夸克质量矩阵m=diagf(mu,md,ms).式(1)中的第二项表示标量道相互作用和赝标量道相互作用，λa是Gell-Mann矩阵；第三项是用来描述U(1)A反常的t’Hooft行列式项.G和K为相互作用常数.这里考虑流夸克质量mu=md≠ms的情形.

在平均场近似下，费米子双线性型可以写成真空期望值和涨落之和，例如：

Mu=mu-4Gφu+2Kφdφs,

(2)

Md=md-4Gφd+2Kφsφu,

(3)

Ms=ms-4Gφs+2Kφuφd.

(4)

这里Mf为夸克的有效质量，φf为夸克凝聚，f是夸克的味道指标.显然，在不考虑U(1)A反常时，K=0，夸克的质量间隙方程是退耦的；正是U(1)A反常使不同味道夸克的有效质量联系起来.味道为f的夸克凝聚定义为

(5)

iSf(p)是味道为f的夸克传播子.电场背景下的传播子写成Schwinger形式是方便的，其在零温度下的表达式为

[(Mf-γ⊥·p⊥)(1-tanh(|qfE|s)γ0γ3)+γ‖·p‖(1-tanh2(|qfE|s))]，

(6)

利用夸克凝聚的定义式(5)及传播子的Schwinger形式(6)，并对动量进行高斯积分，可以得到零温度下的夸克凝聚

(7)

其中,εf=|qf|E.在引入温度T和化学势μ时，需做如下代换：

(8)

把夸克凝聚分解为零温度部分和有限温度部分是为了方便对零温度部分进行正规化.

2 磁化率

磁化率是研究相变系统的重要物理量，可用来揭示一些与相结构相关的重要信息，例如:磁化率可以用来定义相变的临界点[17-23].对于一阶相变，相关磁化率会在相变临界点处发生间断，但相变点左右两侧的磁化率都是有限的；而对于二阶相变，在相变临界点处磁化率同样会出现间断，但相变点的左右两侧都是无穷大.通常，对于严格的一阶或二阶相变，不同的磁化率确定的临界点是相同的.而对于非严格的相变，例如平滑过渡，不同的磁化率确定的临界点可能会有所不同.

本文中使用以下3种磁化率：

(1)热磁化率，定义为

(9)

(2)电磁化率，定义为

(10)

(3)手征磁化率，定义为

(11)

这里φ是手征凝聚，M是夸克的有效质量.可以利用磁化率的峰值确定临界点.既然在NJL模型下有效质量同样是手征相变的重要特征量，采用了有效质量和夸克凝聚两种方式定义磁化率.而计算表明，两种方式定义的磁化率给出的临界值相同.

3 计算结果与讨论

工作的重点是研究零化学势下，不同磁化率确定的电场-温度平面上的手征相变线的差异.在计算手征凝聚时，采用三维动量截断的正规化方法处理零温度部分产生的紫外发散；而有限温度部分，由于不存在发散，无需进行正规化.为避免因电场的引入而引起的红外发散，在计算中取主值积分(这里不考虑夸克的对产生).输入参数取为[16]：三维动量截断Λ=631.4 MeV，mu=md=5.5 MeV，ms=135 MeV，GΛ2=1.835，KΛ5=9.29.

首先考虑夸克的有效质量及凝聚随温度、电场的变化.电场强度eE=0.1GeV2，eE=0.15GeV2，eE=0.2GeV2下有效质量随温度的变化见图1～图3.显然随着温度的升高，夸克的有效质量不断减小.u、d夸克的有效质量下降较快，最终接近其流质量.s夸克的有效质量随温度的变化较为平缓，预示着高得多的相变温度，可以与Λ～600 MeV而相比拟.这个相变温度接近或超出NJL模型的有效能区，因此下面不再讨论s夸克的相变临界点.u、d夸克有效质量的变化表明，在较低温度时，系统是手征对称性自发破缺的，随着温度的升高进入到过渡区域，最后当有效质量接近流质量时，系统基本进入手征对称性(部分)恢复状态.另一方面，电场增强会使相变温度降低，说明电场会削弱手征凝聚.

图1 eE=0.1,0.15，0.2GeV2时u夸克的有效质量-温度曲线Fig.1 The effective mass-temperature curves for the u quark at eE=0.1，0.15， and 0.2GeV2

图2 eE=0.1,0.15，0.2GeV2时d夸克的有效质量-温度曲线Fig.2 The effective mass-temperature curves for the d quark at eE=0.1，0.15， and 0.2GeV2

图3 eE=0.1,0.15，0.2GeV2时s夸克的有效质量-温度曲线Fig.3 The effective mass-temperature curves for the s quark at eE=0.1，0.15， and 0.2GeV2

当把eE=0.2GeV2时夸克的有效质量随温度的变化进行比较时(见图4)，可以看到，u夸克的有效质量因电场的存在要比d夸克小，u夸克进入手征(部分)恢复状态更早，既然u、d夸克的流质量相同，它们有效质量的差异显然是电场导致的.图5以u夸克为例，给出了凝聚在eE=0.1GeV2，eE=0.15GeV2，eE=0.2GeV2时随温度的变化情况，显然其物理结论与对有效质量进行分析得到的结论是一致的.

图4 eE=0.2GeV2时夸克的有效质量-温度曲线Fig.4 The effective mass-temperature curves for the quarks at eE=0.2GeV2

图5 eE=0.1，0.15，0.2GeV2时u夸克的夸克凝聚-温度曲线Fig.5 The quark condensation-temperature curves for the u quark at eE=0.1，0.15， and 0.2GeV2

图6～图8给出了温度T=0.05、0.1及0.15 GeV时夸克的有效质量随电场变化的情况.与温度的增加类似，电场的增强同样会导致夸克有效质量的减少.电场的增强使u、d夸克从手征对称性破缺状态平滑过渡到手征对称性(部分)恢复状态.图9给出了T=0.05 GeV时，3种夸克有效质量随温度的变化情况.因为u、d夸克的流质量相同，所以在不存在电场时，两者具有相同的有效质量.而随着电场的增强，两者的有效质量差异首先不断加大，这是它们带有不同电荷的反映；接下来随着系统向手征对称性恢复相的转变，它们的有效质量的差异又开始变小，最后达到相同流夸克质量的简并状态.

图6 T=0.05，0.1，0.15 GeV时u夸克的有效质量-电场强度曲线Fig. 6 The effective mass-electric field strength curves for the u quark at T=0.05，0.1, and 0.15 GeV

图7 T=0.05，0.1，0.15 GeV时d夸克的有效质量-电场强度曲线Fig.7 The effective mass-electric field strength curves for the d quark at T=0.05，0.1, and 0.15 GeV

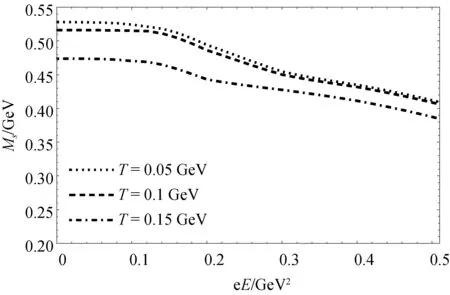
图8 T=0.05，0.1，0.15 GeV时s夸克的有效质量-电场强度曲线Fig.8 The effective mass-electric field strength curves for the s quark at T=0.05，0.1, and 0.15 GeV

图9 T=0.05 GeV时夸克的有效质量-电场强度曲线Fig.9 The effective mass-electric field strength curves for the quarks at T=0.05 GeV

下面采用式(9)～式(11)定义的磁化率讨论(伪)临界点，进而给出相变线.如前所述，从磁化率不仅可以给出(伪)临界点，还能够确定相变的阶.可以从后面的结果看到，对于采用的电场及温度范围，相变既不是一阶相变也不是二阶相变，而是平滑过渡.

图10和图11是不同电场强度下u、d夸克的热磁化率随温度变化的情况，这里的磁化率是用夸克的有效质量定义的.为了对比，在图12中也给出了由夸克凝聚定义的热磁化率的情况，显然两者确定的临界温度是相同的.对确定的电场值可以画出磁化率随温度变化的曲线，其峰值对应的温度，就是该电场强度下的临界温度.让电场强度从0开始不断增大，就得到了由热磁化率确定的E-T平面上的临界线(图20中的χT).

图10 eE=0.1，0.15，0.2GeV2时u夸克的热磁化率-温度曲线,这里的热磁化率由有效质量定义Fig. 10 The thermal susceptibility-temperature curves for the u quark at eE=0.1，0.15，and 0.2GeV2，here the thermal susceptibility is defined by the effective mass

图11 eE=0.1,0.15，0.2GeV2时d夸克的热磁化率-温度曲线,这里的热磁化率由有效质量定义Fig.11 The thermal susceptibility-temperature curves for the d quark at eE=0.1，0.15, and 0.2GeV2，here the thermal susceptibility is defined by the effective mass

图12 eE=0.1，0.15，0.2GeV2时u夸克的热磁化率-温度曲线,这里的热磁化率由夸克凝聚定义Fig.12 The thermal susceptibility-temperature curves for the u quark at eE=0.1，0.15，and 0.2GeV2，here the thermal susceptibility is defined by the quark condensation

类似地，可以通过计算电磁化率得到由电磁化率确定的E-T平面上的临界线(图20中的χE).例如，图13是不同温度下，由有效质量定义的u夸克的电磁化率随电场的变化情况，其峰值对应于相应的临界电场值.

图13 T=0.05，0.1，0.15 GeV时u夸克的电磁化率-电场强度曲线，这里电磁化率由有效质量定义Fig.13 The electric susceptibility-electric field strength curves at T=0.05，0.1, and 0.15 GeV，here the thermal susceptibility is defined by the effective mass

利用手征磁化率确定相变的临界线存在两种方式.一种是在给定的电场强度下，考察手征磁化率峰值对温度变化的情况(图20中的χST)；另一种方式是在给定的温度下，考察手征磁化率随电场强度变化的情况(图20中的χSE).这两种方式给出的临界值有所不同.图14、图15是不同电场强度下由有效质量定义的u、d夸克的手征磁化率随温度的变化情况，在图16、图17展示了利用夸克凝聚定义的结果，显然确定的临界值是相同的.类似的，不同温度下手征磁化率随电场的变化情况见图18和图19.

图14 eE=0.1，0.15，0.2GeV2时u夸克的手征磁化率-温度曲线，这里的手征磁化率由有效质量定义Fig.14 The chiral susceptibility-temperature curves for the u quark at eE=0.1， 0.15, and 0.2GeV2，here the chiral susceptibility is defined by the effective mass

图15 eE=0.1，0.15，0.2GeV2时d夸克的手征磁化率-温度曲线，这里的手征磁化率由有效质量定义Fig. 15 The chiral susceptibility-temperature curves for the d quark at eE=0.1， 0.15, and 0.2GeV2，here the chiral susceptibility is defined by the effective mass

图16 eE=0.1，0.15，0.2GeV2时u夸克的手征磁化率-温度曲线，这里的手征磁化率由夸克凝聚定义Fig.16 The chiral susceptibility-temperature curves for the u quark at eE=0.1， 0.15, and 0.2GeV2，here the chiral susceptibility is defined by the quark condensation

图17 eE=0.1，0.15，0.2GeV2时d夸克的手征磁化率-温度曲线，这里的手征磁化率由手征凝聚定义Fig.17 The chiral susceptibility-temperature curves for the d quark at eE=0.1， 0.15, and 0.2GeV2，here the chiral susceptibility is defined by the quark condensation

图18 T=0.05，0.1，0.15 GeV时u夸克的手征磁化率-电场强度曲线，这里的手征磁化率由有效质量定义Fig.18 The chiral susceptibility-electric field strength curves for the u quark at T=0.05，0.1, and 0.15 GeV，here the chiral susceptibility is defined by the effective mass

图19 T=0.05，0.1，0.15 GeV时d夸克的手征磁化率-电场强度曲线，这里的手征磁化率由有效质量定义Fig.19 The chiral susceptibility-electric field strength curves for the d quark at T=0.05，0.1, and 0.15 GeV，here the chiral susceptibility is defined by the effective mass

利用上述方法，采用热磁化率、电磁化率及手征磁化率(确定临界点有两种不同方式)确定了化学势为0时u夸克在E-T平面上的手征相变临界线，见图20.从前面的计算可知，d夸克的相变临界点与u夸克差异不大，既然主要考察不同磁化率在确定临界线上的差异，在此仅以u夸克为例加以说明.不同磁化率确定的手征相变临界线是相似的，但存在定量上的差异.在手征相变临界线的中段，不同的磁化率确定的临界线差异较为明显.因此，在平滑过渡的情况下，把不同磁化率确定的临界线综合考虑是更合适的，比如取不同临界线围成的带状区域.

图20 由不同磁化率确定的E-T平面相图Fig.20 Phase diagram in the E-T plane determined by different susceptibilities

4 结 论

本文采用NJL模型对恒定电场背景下强相互作用物质的手征相变进行了研究.结果表明，电场具有破坏手征凝聚的作用，导致相变临界温度降低，而且所带电荷的差异导致了u夸克的手征对称性恢复要比d夸克快.夸克的有效质量(或凝聚)随电场和温度的变化表明相变为平滑过渡，磁化率曲线的连续性也证实了这一点.采用热磁化率、电磁化率和手征磁化率等几种不同的磁化率确定了电场-温度平面的相变临界线，发现利用不同磁化率的峰值确定的相变临界线存在差异，特别在手征相变临界线的中段，差异较为明显.因此，在平滑过渡的情况下，使用由不同磁化率确定的临界线围成的带状区域更为合适.此外，在NJL模型下，使用夸克有效质量定义的磁化率与夸克凝聚定义的磁化率确定的临界点是相同的.