外平面图的距离2-点可区别边色数*

王维凡,王琰雯,黄丹君

(浙江师范大学 数理与信息工程学院,浙江 金华 321004)



外平面图的距离2-点可区别边色数*

王维凡,王琰雯,黄丹君

(浙江师范大学 数理与信息工程学院,浙江 金华 321004)

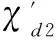
边染色;距离2-点可区别边染色;外平面图;最大度

0 引 言

本文考虑的图都是有限简单图.设V(G),E(G),Δ(G),δ(G)分别表示图G的顶点集、边集、最大度和最小度.用NG(v)表示与顶点v相邻的点集合,因此,dG(v)=|NG(v)|是v在图G中的度.用dG(u,v)表示2个点u和v在G中的距离,即连接它们的最短路的长度.在不引起混淆的情况下,分别将Δ(G),NG(v),dG(v),dG(u,v)简记为Δ,N(v),d(v),d(u,v).一个k-点(k+-点或k--点)是一个度数为k(至多为k,或者至少为k)的点.对i≥1,用ni(v)表示与点v相邻的i-点的个数．若一个图G没有孤立边,就称它是正常的.图G的一个正常k-边染色是指一个映射φ:E(G)→{1,2,…,k},使得相邻的边染不同的颜色.对于一个点v∈V(G),用Cφ(v)表示所有与v相关联的边得到的颜色集合,即Cφ(v)={φ(uv) |uv∈E(G)}.

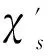
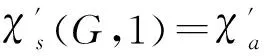
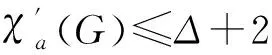
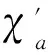
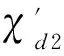
本文研究外平面图族的距离2-点可区别边染色问题,证明了:任意外平面图G的距离2-点可区别的边色数不超过2Δ.

1 结构引理

若一个图能嵌入到欧几里得平面上,使得所有点都出现在无界面的边界上,则称这个图为外可平面图.外平面图是外可平面图在欧几里得平面上的一个嵌入.设G是一个外平面图,用F(G)表示G中面的集合.对于f∈F(G),用b(f)表示f的边界,并且若u1,u2,…,un是b(f)上沿顺时针方向的点,则记f=[u1u2…un].一个度为1的顶点也称为一个叶子.

为了刻画外平面图的边-面全色数,王维凡等[11]证明了下面的结构引理：

引理1 设G是一个外平面图,且δ(G)=2,那么G必含有下面子构型之一(见图 1):

1)一条路x1x2x3x4满足d(x2)=d(x3)=2;

2)一个3-面[uv1v2]满足d(u)=2,d(v1)=3;

3)2个3-面[xu1v1]和[xu2v2]满足d(u1)=d(u2)=2,d(x)=4.

(a) (b) (c) 图1 引理1中G的3个子图

图1中,若与一个点相关联的边都画出来了,也即这个点的度数确定了,就用实心点来表示;否则,就用空心点来表示.

引理2 每一个至少有2个顶点的连通图G必含有下面的子构型之一:

1)一个度数至多为3的顶点v与叶子相邻,或者一个4+-点v至多相邻于2个非叶子点;

2)一条路x1x2x3x4满足d(x2)=d(x3)=2;

3)一个3-面[uv1v2]满足d(u)=2,d(v1)≥3且n1(v1)=d(v1)-3;

4)2个3-面[xu1v1]和[xu2v2]满足d(u1)=d(u2)=2,d(x)≥4和n1(x)=d(x)-4.

证明 采用反证法.假设G不包含1)～4)中任意一个.因为G不含有1),所以G没有3--点相邻于叶子,而且每一个4+-点v至多与d(v)-3个叶子相邻,也就是说它至少有3个邻点不是叶子.

设H是由G去掉所有叶子之后得到的图,那么H是一个连通的外平面图.设v∈V(H),因为V(H)⊆V(G),所以由H的定义可知dG(v)≥2.若2≤dG(v)≤3,则dH(v)=dG(v)≥2;若dG(v)≥4,则dH(v)=dG(v)-n1(v)≥dG(v)-(dG(v)-3)=3.因此,δ(H)=2.由引理1知,H包含图1 中的子图形 (a),(b)和(c)之一.注意到：若dH(v)=2,则dG(v)=2.所以,容易观察到G至少包含引理2中的2),3)和4)之一,与G的假设相矛盾.引理2证毕.

下面2个引理是很容易被证明成立的:

引理3 设Pn是一条长为n≥2的路,则

引理4 设Cn是一个长为n≥3的圈,则

2 主要结果

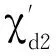
1)G包含一个3--点v,使得n1(v)≥1;或者G包含一个4+-点 v,使得n1(v)≥k-2,即为引理2中的1).

设v1,v2,…,vk是v的邻点,其中k=d(v)且v1是G的一个叶子.下面分为2个子情形.

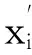
②k≥4.那么n1(v)≥k-2.假设d(vi)=1,i=1,2,…,k-2,且令H=G-{v1,v2,…,vk-2}.则由归纳假设知,H有一个应用颜色集合C的距离2-点可区别边染色φ.不失一般性,设φ(vvk-1)=1,φ(vvk)=2.注意到点v至多有2Δ-2个距离为2的点.由于

所以一定存在一个(k-2)-元子集 C′⊂C{φ(vv1),φ(vv2)},使得vv1,vv2,…,vvk-2可以应用集合C′进行合法染色.因此,可得到图G的一个距离2-点可区别2Δ-边染色.

2)G包含一条路x1x2x3x4,使得d(x2)=d(x3)=2,即为引理2中的2).

如果x1与x4重合,那么图G-x2x3有一个应用颜色集合C的距离2-点可区别边染色φ.由于x2x3有2个禁用色,且x2,x3至多有Δ-2个距离为2的顶点,|C|=2Δ,因此可以对x2x3进行合法染色,从而得到图G的一个距离2-点可区别2Δ-边染色.

下面假设x1≠x4.设H是由图G通过收缩边x2x3成为一个新点w后而得到的图,那么H是一个满足|T(H)|<|T(G)|的简单外平面图.由归纳假设,H有一个应用颜色集合C的距离2点可区别边染色φ,使得φ(wx1)=1且φ(wx4)=2.基于φ,在图G中,把x1x2染成颜色1,把x3x4染成颜色2.若x2x3不能被合法染色,则d(x1)=d(x4)=Δ,Cφ(yi)={1,2+i},i=1,2,…,Δ-1,且Cφ(zj)={2,Δ+1+j},j=1,2,…,Δ-1,其中y1,y2,…,yΔ-1是x1的不同于x2的邻点,z1,z2,…,zΔ-1是x4的不同于x3的邻点.因此,φ(x1yi)=2+i 且φ(x4zj)=Δ+1+j.把x1x2改染成2,把x2x3染成1,由此就得到图G的一个距离2-点可区别2Δ-边染色.

3)G包含一个3-面[uv1v2]满足d(u)=2,d(v1)=k≥3和n1(v1)=k-3,即为引理2中的3).

基于2)的证明,可以假设d(v2)≥3.设u,w,v2,x1,x2,…,xk-3是v1的邻点,其中d(x1)=d(x2)=…=d(xk-3)=1.下面分为2种子情形.

①k≥4.设H=G-{x1,x2,…,xk-3}.由归纳假设知,H有一个应用颜色集合C的距离2-点可区别边染色φ,使得φ(wv1)=1,φ(v1v2)=2及φ(uv1)=3.注意到v1至多有(Δ-1)+(Δ-2)=2Δ-3个距离为2的k-点.若k≥5,则由

知,一定存在一个(k-3)-元子集C′⊂{4,5,…,2Δ},使得v1x1,v1x2,…,v1xk-3可以应用颜色集合C′进行合法染色,这样就得到了图G的一个距离2-点可区别2Δ-边染色.因此,下面假设k=4.若v1x1不能够被合法染色,那么对所有的i=4,5,…,2Δ,{1,2,3,i}是v1的某个距离为2且度数为4的顶点的颜色集合.所以,v1的所有距离为2的点都是4-点.在{4,5}{φ(uv2)}中选取一个颜色来改染v1u,然后把v1x1染成颜色6即可.

②k=3.令 H=G-uv1.由归纳假设知,H有一个应用颜色集合C的距离2-点可区别边染色φ,使得φ(uv2)=1,φ(v1v2)=2和φ(wv1)=a.先设d(w)=2.若a=1,则u和v1总共至多有Δ个距离为2的点.因为Δ≥3且|C{1,2}|=2Δ-2>Δ,所以可以在C{1,2}中选取一个颜色对uv1进行合法染色.若 a≠1,不妨设a=3,则只要用{4,5,2Δ}给边uv1正常染色,u与w的颜色集合就不同.故u和v1总共至多有Δ-1个距离为2的点.因为Δ≥3且|C{1,2,3}|=2Δ-3>Δ-1,所以可以在C{1,2,3}中选取一个颜色对uv1进行合法染色.这样就得到了图G一个距离2-点可区别2Δ-边染色.

现在,假设d(w)≥3,那么在图G中,u和v1总共至多有(Δ-1)+(Δ-2)=2Δ-3个冲突点.若a=1,则|C{1,2}|=2Δ-2>2Δ-3,可以在C{1,2}中选取一个颜色对uv1进行合法染色.所以,下面假设a≠1,不妨设a=3.若 uv1不能够被合法染色,则假设{{2,3,i} | i=4,5,…,Δ+2}={Cφ(x)|x∈N(w){v1}},且{2,3,j}或{1,j}(j=Δ+3,Δ+4,…,2Δ)是v2的某些邻点的颜色集合.在这种情况下,把uv2和v1v2的颜色互换,把uv1染成颜色4即可.

4)G包含2个3-面[xu1v1]和[xu2v2]满足d(u1)=d(u2)=2,d(x)=k≥4和n1(x)=k-4,即为引理2中的4).

基于2)的证明,可以假设d(v1)≥3且d(v2)≥3.设y1,y2,…,yd(v1)-2是v1的不同于x和u1的邻点,z1,z2,…,zd(v2)-2是v2的不同于x和u2的邻点.同时,用x1,x2,…,xk-4表示x的不同于u1,u2,v1,v2的邻点.由定义知,对所有的i=1,2,…,k-4,都有d(xi)=1.需要讨论下面2种可能性:

①k≥5.设H=G-{x1,x2,…,xk-4}.由归纳假设知,H有一个应用颜色集合C的距离2-点可区别边染色φ,使得φ(xv1)=1,φ(xu1)=2,φ(xu2)=3及φ(xv2)=4.注意到x至多有2(Δ-2)=2Δ-4个距离为2的k-点.若k≥6,则由

知,存在一个(k-4)-元子集C′⊂C{1,2,3,4},使得xx1,xx2,…,xxk-4可以使用颜色集合C′进行合法染色.因此,下面假设k=5.若 xx1不能够被合法染色,则d(v1)=d(v2)=Δ,且对每一个i=5,6,…,2Δ,{1,2,3,4,i}是{y1,y2,…,yΔ-2,z1,z2,…,zΔ-2}中的一个顶点的颜色集合,这就意味着{y1,y2,…,yΔ-2,z1,z2,…,zΔ-2}中的每一个点都是5-点.为了得到图G的一个距离2-点可区别2Δ-边染色,只需在{5,6}{φ(v1u1)}中选取一个颜色改染xu1,然后把xx1染成颜色7即可.

②k=4.由归纳假设知,G-xu1有一个应用颜色集合C的距离2-点可区别边染色φ,使得φ(xv1)=1,φ(xu2)=2,φ(xv2)=3,φ(u1v1)=a.注意到a≠1,因此,需要考虑下面2种情况.

i)a∈{2,3}.

易见,x和u1在图G中总共至多有2Δ-3 个冲突点.若xu1不能够被合法染色,则d(v1)=d(v2)=Δ.进而进一步假设:Cφ(u2)={2,4};Cφ(zi)={1,2,3,i+4},i=1,2,…,Δ-2;Cφ(yi)={a,i+Δ+2}或者{1,2,3,i+Δ+2},i=1,2,…,Δ-2.所以φ(u2v2)=4.互换u2v2和xv2的颜色,然后把xu1染成颜色5,就得到了图G的一个距离2-点可区别2Δ-边染色.

ii)a∉{2,3},令 a=4.

若xu1能够被正常染色,则u1和u2将得到不同的颜色集合.此外,x和u1在图G中总共至多有2Δ-4个冲突点.若xu1不能够被合法染色,则推出d(v1)=d(v2)=Δ,且可以假设Cφ(zi)={1,2,3,i+4},i=1,2,…,Δ-2;Cφ(yi)={a,i+Δ+2}或者{1,2,3,i+Δ+2},i=1,2,…,Δ-2.这时可以把u1v1和xv1的颜色互换,然后把xu1染成颜色5,就得到了G的一个距离2-点可区别2Δ-边染色.定理1证毕.

[1]Akbari S,Bidkhori N,Nosrati N.r-Strong edge colorings of graphs[J].Discrete Math,2006,306(23):3005-3010.

[2]Zhang Zhongfu,Li Jingwen,Chen Xiangen,et al.D(β)-vertex-distinguishing proper edge-coloring of graphs[J].Acta Math Sinica:Chin Ser,2006,49(3):703-708.

[5]Bazgan C,Harkat-Benhamdine A H,Li Hao,et al.On the vertex-distinguishing proper edge-colorings of graphs[J].J Combin Theory Ser B,1999,75(2):288-301.

[6]Burris A C,Schelp R H.Vertex-distinguishing proper edge-colorings[J].J Graph Theory,1997,26(2):73-82.

[7]Zhang Zhongfu,Liu Linzhong,Wang Jianfang.Adjacent strong edge coloring of graphs[J].Appl Math Lett,2002,15(5):623-626.

[8]Balister P N,Györi E,Lehel J,et al.Adjacent vertex distinguishing edge-colorings[J].SIAM J Discrete Math,2007,21(1):237-250.

[9]Hatami H.Δ+300 is a bound on the the adjacent vertex distinguishing edge chromatic number[J].J Combin Theory Ser B,2005,95(2):246-256.

[10]Horňák M,Huang Danjun,Wang Weifan.On neighbor-distinguishing index of planar graphs[J].J Graph Theory,2014,76(4):262-278.

[11]Wang Weifan,Zhang Kemin.Δ-matchings and edge-face chromatic numbers[J].Acta Math Appl Sin,1999,22(2):236-242.

(责任编辑 陶立方)

Distance vertex-distinguishing index of outerplanar graphs

WANG Weifan,WANG Yanwen,HUANG Danjun

(CollegeofMathematics,PhysicsandInformationEngineering,ZhejiangNormalUniversity,Jinhua321004,China)

edgecoloring; 2-distance vertex-distinguishing index; outerplanar graph; maximum degree

10.16218/j.issn.1001-5051.2016.01.001

��2015-05-27；

2015-09-02

国家自然科学基金资助项目(11371328;11301486)

王维凡(1955-)，男，辽宁沈阳人，教授，博导.研究方向：图论与组合优化.

O157.5

A

1001-5051(2016)01-001-05