基于形态变换的帽饰图案的适应性

高先科， 徐蓼芫， 徐平华， 周佳

(南通大学 纺织服装学院，江苏 南通 226019)



基于形态变换的帽饰图案的适应性

高先科， 徐蓼芫*， 徐平华， 周佳

(南通大学 纺织服装学院，江苏 南通 226019)

从帽身与帽沿的需求出发，利用图像形态变换实现帽饰图案的变形与对位。阐述了扇形几何形态变换的原理，利用直角坐标与极坐标的坐标转换关系实现图像像素点位置的匹配；分别从彩色图像的RGB 3个通道对图像形态进行变换，形成多通道扇形灰度图；在此基础上，将多幅灰度图像再合成真彩色图像，最终实现彩色图案在样板间弧线联接处的准确对位。此研究有利于提升传统纹样设计、加工效率和外观效果，为纺织品的快速化生产提供技术支持。

形态变换；坐标转换；样板；对位

纺织品表面的喷绘、烫印及绣花工艺，要适应其外观立体造型的需求，就要对规则图案进行样板适应性变形处理。这一问题困扰着纺织企业的生产者，需要寻找一种高效且切实可行的办法。最为典型的是帽身与帽沿的衔接处、汽车座套等曲面外形处的图案立体印制，需要对图案做几何状变形处理。服饰图案与纸样的形态吻合度决定了产品的视觉传达效果，平面纸样到服饰品的设计加工过程要求印花、刺绣纹样具有较强的形态适应性。传统的“对条对格”工艺并不能完全解决此类问题。因此，需要寻找一种新方法。

传统的图案设计与加工方法很少对原始图案作变形处理。对于图案变形算法，经典的算法有基于表达特征的图案变形技术[1]，如时永杰、黄武、杨金钟[2- 4]等人提出的基于网格、线段和控制点图案变形方法；基于径向基函数插值、轮廓和扩展的移动最小二乘法等图案变形算法[5-9]。在变形运用研究上，有图案变形对标志设计的作用[10]、基于图案变形的投影融合技术[11]和图案变形的膜内装饰技术等[12-13]。这些方法大都使得图案变形后更具创新感，给人以美的视觉享受；或者研究的重点是单纯的一种算法的改进或创新，不具有针对性，因而不足以解决文中提出的纸样与纸样间弧线接缝处的图案对位问题。

为此，文中从帽身与帽沿设计需求出发，提出利用图像的形态变换原理和像素点坐标转换关系，对图案进行扇形状的几何变形处理，实现图案在类似弧线处的重新对位，以提高图案在帽饰上的形态适应性。

1 算法流程与原理

1.1 算法流程

文中提出图案变扇形算法的主要流程：

1) 获取原图矩阵大小：使用工具箱里相关函数获取原始矩形图像矩阵的维度、大小等信息；

2) 设定目标扇形区域：依据目标扇形图所对应的圆心角、半径，和原矩阵大小等相关参数，利用有关函数设定扇形区域；

3) 划分扇形区域网格：根据下文的形态变换原理，将设定的扇形区域划分成与原矩形图的像素点相等数量的网格，即一个像素点相当于一个小网格；

4)完成像素点赋值：扇形中每一个网格对应原图中一个像素点。按照直角坐标系和极坐标系的坐标转换关系，可以找出扇形中每一个网格所对应矩形中的像素点，将所对应像素点的值赋值给网格。

上述图案变形的算法流程可以用流程图简单表示，如图1所示。

1.2 算法原理

以上介绍了文中算法的整体框架及流程，下面分节介绍算法的主要原理。

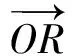
通常取平面中任意一点为P点，在直角坐标系中可用有序数对(x,y)来表示。图2是极坐标系中任意一点到直角坐标系中对应点的转换关系示意图。

P点的横坐标x=ON，纵坐标y=PN。在直角三角形OPN中，根据三角函数关系，可得

(1)

则可得极坐标系坐标与直角坐标系坐标间的转换关系：

(2)

1.2.2 形态变换基本原理 图3反应了矩形到扇形的形态变换中S与S′的映射关系。文中采用划分网格法实现这种不同坐标系下的映射关系。任何一幅灰度图像是一个M×N的二维矩阵(彩色图像为M×N×3的三维矩阵)[14]，可以看成是一个由M×N个小矩形组成的网格，每个小网格代表一个像素点，其中AC=M，AB=N。同理,可以将目标扇形区域A′B′C′D′分割成数量相等的M×N个小网格，每个小网格与矩形中的每个像素点对应，即要求A′C′=M,A′B′=N。

扇形图像中任意一点S′在极坐标系下的坐标为(ρ,θ)，根据坐标转换关系可以得出原矩形图像中对应像素点的坐标：

x=ρ×cos(θ)和y=ρ×sin(θ)

把对应矩形中像素点的像素值赋值给扇形中的点S′，遍历扇形图中每个网格完成像素点的赋值。

另外，扇形区域的确定由圆心角α和半径部分A′C′决定,而圆心O固定，A′C′=A′O-C′O，因此设定C′O的值和圆心角α就可以确定变形的扇形区域。

2 图案的位置对位与图案的变形

2.1 图案的位置、对位

2.1.1 确定位置 帽身与帽沿处图案对位，主要是在帽前片与帽舌拼接处，因此需要先对整幅图案进行分割成上下两部分(帽前片和帽舌处),然后确定各个部分在帽前片和帽舌上的具体位置。可以看出此处提出确定图案的位置，准确地说是图案在其对应纸样上重新对位时的准确位置。

2.1.2 图案对位 实现图案在这种弧线位置对位，需要注意以下两点。一方面，要求帽前片与帽舌上的两部分图案在拼接处对位，但帽身与帽舌拼接处是条弧线，这是由拼接的帽前片与帽舌的样板形状决定的。对图案进行分割，分割后图案的边缘一般都是直线。因此，要分割后图案重新对位，需要将图案边缘的直线变成弧线，即图案要变成有弧线边缘的扇形。 另一方面， 要保证图案成功

重新对位，还需要图案经过变形后，对位时边缘的两弧线长度一致。

从上述分析可以看出，由于帽身与帽舌处拼接的地方是弧线，需要对分割后的图案进行变形才能重新对位，这是对位的依据；而图案对位时必须保证变形后两边缘弧线相等，这是对位的关键。

2.2 图案的变形

2.2.1 弧线的确定 弧线是整个图案对齐的关键，所以必须准确确定弧线的弧长与弧度。文中提出把弧线近似地看成扇形的弧长，根据不在一条直线上的任意3点可以确定一个圆，因此根据此弧线可以确定其所在的扇形，如图4所示。同时可以获得弧线对应的圆心角α和半径r，作为设定扇形形状的主要参数。还可以根据弧长公式和圆心角α、半径r计算出弧长，因为保证图案两部分弧线长相等是重新对位的关键。

2.2.2 图案的变形 图案的变形是在Matlab软件中通过编程来完成的，具体过程见文中“实验与讨论”部分。以2.2.1节中获得扇形的圆心角和扇形半径作为设定扇形区域参数的依据，以此确定变形后扇形的具体形状；再利用形态变换原理实现扇形变换，最终得到变形后的扇形图案，如图5所示。需要注意，变形后的弧线长度应与图案另一部分对位时的边缘长度一致。

1.城市公共绿地少，且分布不均，中心城区公园绿地面积17.0hm2，人均公园绿地仅为1.3m2，居住区无大型公共绿地。城区内已建成的两处公园，服务设施尚不完善，不配套。缺乏形式美、自然美、意境美；街头绿地少，没有形成街头小环境。

图案的变形主要目的是将边缘变为弧线的形状，便于吻合纸版，且要保证对位时弧线长度一致，这样可使得整幅图案在帽身与帽沿联接处重新准确对位，如图6所示。

3 实验与讨论

3.1 实验素材

实验的图案均来自企业生产中帽饰上所采用的印绣花图案。

3.2 实验软件

实验采用的软件Matlab.2014a，该软件具有强大的图像处理功能，且具有实用性强、程序移植性高的特点。图像处理工具箱里的函数包含许多算法，可以直接使用，这样提高了编写程序的效率。

3.3 实验过程

实验采用Matlab.2014a软件编程来完成图案的变形。首先，根据图案对位时的弧线得出对应扇形圆心角和半径，实验取半径r=2 000和圆心角α=80°,然后依据原图像矩阵的大小和上述参数设定扇形区域，如图7(b)所示，再将扇形区域划分成与原图矩阵像素点相等数量的网格，如图7(c)所示,最后根据坐标转换关系，完成扇形中每个网格(像素点)的赋值。达到实现图案变形的目的，如图7(d)所示。

彩色的RGB图像处理，通常是先将RGB彩色图像分为R，G，B3个通道分别进行处理，得到3个通道的灰度图像，处理完成后再合成最终需要的彩色图像。

图案对位是建立在把分割后的图案部分变成扇形的基础上，此种矩形图案变扇形图案的方法也适用于整幅图案。根据以上过程可知，目标扇形图案的具体形状是由弧线决定的，而不同的弧线所对应的扇形圆心角α与扇行半径r也有所不同。因此，可设定不同的r和α值，以获得不同的扇形形状来满足不同弧线的对位要求，如图8所示。

从变形结果可以得出，图案变形只是改变图案的形状和轮廓，并未对图案色彩、纹理等造成任何不利影响。从横向看，当r值相同时(r=1 000)，α值越大，扇形弧度越大，离圆心较远的像素点左右方向扩散感越明显；从纵向看，当α相同时(α=90°)，r值越小，离圆心较近的像素点挤压感越强烈。从图案整体看，离圆心越近的像素点形成挤压感，离圆心越远的像素点形成扩散感。这是因为像素点到圆心的距离越远，变换角度越大，则像素点位置变换的弧线越长造成的。

由以上分析可知，要获得自己想要的变形效果，合理设置参数α和r的值十分重要。根据不同的弧线可以设定不同参数的圆心角与半径。但该弧线能够近似地拟合成扇形弧，对于复杂的弧线，如衣袖袖山与肩部拼接时的弧线等，就不一定适用了，这方面可以成为后续研究的方向。另一方面，从审美视觉角度看，变形后的扇形图案还具有一定的新颖性。

除了上述实验中的图案，各种类型的图案按文中提供的程序，设定r和α值都可以进行任意扇形的形变。如图9所示，选定Logo图案、几何造型图案、花型图案和带有线条图案，设定统一的参数进行扇形变形(其中r=1 000和α=90°)。

此外，传统的标准矩形变形算法会出现变形后图像中在不同位置的像素点具有相同位置的情况[15]，使得一些像素点取舍困难，图案变形后会出现一定程度的失真。文中采用的是这种基于划分网格的变形算法，能够避免此类问题的出现。可以看出，使用文中提出的算法，图案变形后外观效果依然十分美观。

在变形速度方面，以一幅尺度为3 264像素×2 448像素，分辨率为72 dpi的色块图(见图8(a))为例，α=90°，r=1 000,图案变形的时间约为1.13 s(硬件配置：CPU为Intel(R) Core(TM) T6570@2.10 GHz，RAM为4 GB)。文中选取的图案变形时间均不小于1.5 s，变形所需时间随着图像分辨率及尺度、目标扇形图案的具体形状和计算机软硬件性能等差异均会有所不同。

4 结语

文中提出利用形态变换和坐标转换关系达到图案变形的目的，实现图案在类似弧线处的重新准确对位，提高图案在产品上的形态适应性。这种对位技术可以广泛地运用到类似纺织品中的图案对位工艺中，如文中的帽身与帽沿衔接处。从而在一定程度上可以提高产品的品质，易获得消费者青睐，也满足了当前服饰行业高档时尚的发展需求。

[1] 邱文杰.基于MLS图像变形技术与实现[D].北京:北京邮电大学,2011.

[2] 时永杰.基于等边三角形网格的交互式二维图像变形技术[D].昆明:云南大学,2013.

[3] 黄武,姚淑波,关胜亮,等.利用控制线段的实时图像变形方法[J].计算机辅助设计与图形学学报,2010,22(12):2067-2072.

HUANG Wu,YAO Shubo,GUANG Shengliang,et al.A real time image deformation method based on line handles[J].Journal of Computer Aided Design and Computer Graphics,2010,22(12):2067-2072.(in Chinese)

[4] 杨金钟,刘政凯,俞能海,等.基于控制点的图像变形方法及其应用[J].中国图像图形学报,2001,6A(11):1070-1074.

YANG Jinzhong,LIU Zhengkai,YU Nenghai,et al.An image warping method based on control points and its applications[J].Journal of Image and Graphics,2001,6A(11):1070-1074.(in Chinese)

[5] Kwon,Jung Hye,Lee,et al.Image deformation using radial basis function interpolation[C]//17th International Conference in Central Europe on Computer Graphics,Visualization and Computer Vision.CZE:Vaclav Skala,2009:9-12.

[6] CHEN Pengfei,WANG Jing.Image deformation based on contour[J].Journal of Computational Information Systems,2014,10(20):8637-8643.

[7] Atanasoaei,Cosmin,Moldoveanu,et al.Extensions to the MLS method for image deformation[J].Journal of Mathematical Image and Vision,2012,42(1):50- 63.

[8] Shahid Farid M,Arif Mahmood.Image morphing in frequency domain.[J].UPB Scientific Bulletin,2008,70(2):3-14.

[9] 肖红光,肖树根,刘京,等.多特征融合图像自动变形[J].中国图像图形学报,2014,19(7):1012-1020.

XIAO Hongguang,XIAO Shugen,LIU Jing,et al.Multi-feature fusion-based image morphing[J].Journal of Image and Graphics,2014,19(7):1012-1020.(in Chinese)

[10] 吕雯雯.装饰造型中的图案变形对现代标志的作用[J].新教育时代电子杂志(教师版),2015(20):320:320.

LV Wenwen.Deformation pattern of decorative styling play a role of a modern logo[J].New Education Era,2015(20):320:320.(in Chinese)

[11] MA Yao,LIU Shufen,HAN Lu.Human Centerd Computering of Lecture Notes in Computer Science[M].Berlin:Springer Verlag,2015:405- 414.

[12] 乐云霞,欧长劲,蒋献峰,等.IMD膜片图案变形评测研究[J].塑料工业,2015,43(3):76-79.

LE Yunxia,OU Changjin,JIANG Xianfeng,et al.Study of the deformation evaluation of pattern of IMD film[J].China Plastics Industry,2015,43(3):76-79.(in Chinese)

[13] 王守觉,梁先扬.图像变形计算方法及其运用[J].计算机辅助设计与图形学学报,2011,23(8):1304-1310.

WANG Shoujue,LIANG Xianyang.Calculation method of image morphing and its application[J].Journal of Computer-Aided Design and Computer Graphics,2011,23(8):1304-1310.(in Chinese)

[14] 张铮,徐超,任淑霞,等.数字图像处理与计算机视觉[M].北京:人民邮电出版社,2014:107-110.

[15] 冯百乐.织物图像变形技术的研究[D].杭州:浙江大学,2008.

(责任编辑：杨勇)

Adaptability of Headwear Pattern Based on Morphology Transformation

GAO Xianke, XU Liaoyuan*, XU Pinghua, ZHOU Jia

(School of Textile and Clothing,Nantong University,Nantong 226019，China)

From the requirements of the hat body and the brim of the hat, the deformation and alignment of the hat pattern is achieved by the image morphological transform. The principle of pattern shape rectangle and fan shape transformation is expound. By using the coordinate transformation between Cartesian coordinates and polar coordinates to match the pixels and image position and the three-color RGB image channel to transform the image morphology, a multi-channel sector gray scale image is formed. Based on this, the true color images are combined by a number of multi-channel sector gray scale images, and finally the accurate alignment in the link of the arc between the true color images and the template is realized. The research is beneficial to improve the processing efficiency and appearance of traditional pattern design, and to provide technical support for the rapid production of textiles.

morphological transform, coordinate transformation, template, alignment

2016-04-15；

2016-05-20。

江苏省大学生实践创新项目(201610304051Z)；南通大学纺织服装学院研究生自主创新项目(FZ201507)。

高先科(1989—)，男，硕士研究生。

*通信作者：徐蓼芫(1957—)，女，副教授，硕士生导师。主要研究方向为服装设计与工程。Email：xu.ly@ntu.edu.cn

TS 941.7

A

2096-1928(2016)04-0381-06