重结论,但绝不可轻过程
张占魁

摘 要:在应试教育体制下,广大初中数学教师课堂采取题海战术,压制学生埋头于茫茫题海之中;课后实施死记方案,督促学生顾首于概念定理之间。魅力无穷的数学面目全非,使人生厌。追本溯源,是因为教师过分注重知识结论,严重忽略知识生成过程导致的。鉴于此,在初中数学课堂中,教师要注重知识结论,但更要关注知识生成的过程。
关键词:数学课堂;知识生成过程;重要性;学习兴趣
数学是思维的体操。数学课堂应该是重探究、训思维、彰显美的课堂;数学课堂应该是注重结论但更看重过程的课堂。然而,令人遗憾的是:在现如今的初中数学课堂中,由于受到应试教育大浪的冲击,广大教师过分注重知识的传授,督促学生死记硬背一些概念、定理等,使得原本充满悬疑、妙趣横生的数学课堂变得枯燥乏味、死气沉沉,数学丧失了它的固有之美。为了使初中数学课堂充满活力、魅力再现,教师必须放下手中指挥的教鞭,走近学生,与学生一起寻根究底、探究问题、亲历过程、形成结论;与学生一起聚焦知识生成的过程,指引学生踏上探究之旅,促使学生开启思维之泉,引领学生领略数学之美。
一、领略数学之美,激发学习兴趣
关注生成的数学课堂琳琅满目,美不胜收。比如,在教学“丰富的图形世界”时,教师摒弃直接用课件或模型展示圆柱、圆锥等几何体的枯燥呆板方式,而是通过课件向学生展示了生活中缤纷多样的立体图形,让学生由生活中的立体图形抽象出数学中的几何体。学生由足球、篮球以及我们赖以生存的美丽地球等抽象出了球体;由锥型灯罩、漏斗以及令人垂涎的冰激凌等抽象出了圆锥体;由包装盒、电冰箱以及鳞次栉比的高楼大厦等抽象出了正方体……生活中各种各样的事物纷至沓来,浮现在学生的眼前。学生经历了从现实图像中抽象出数学图形的过程,在感受现实世界的丰富多彩之际,充分领略到数学之美。
二、踏上探究之旅,培养自学能力
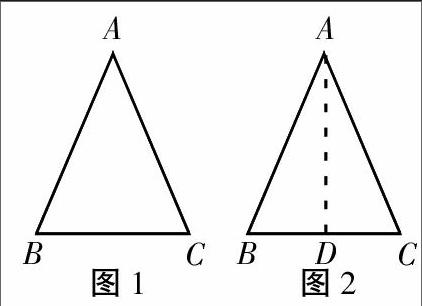
关注生成的数学课堂疑云密布,妙不可言。如,在教学“三角形的证明”时,教师不是直接让学生去记忆等腰三角形两底角相等的性质,而是与学生一起利用已知的结论来推导。教师首先课件展示了一个等腰三角形△ABC(如图1),并指出:既然是等腰三角形,那么就已知:在△ABC中,AB=AC。求证:∠B=∠C。学生感到迷惑不解,茫然不知如何求证。教师启发:我们曾经用折叠的方法说明了两个底角相等,折痕将等腰三角形分成了两个全等三角形。学生甲灵光一闪举手指出:我们可以把这条折痕看做是一条辅助线(如图2)。教师点头微笑予以肯定,并要求学生分组求证。片刻之后,某小组汇报如下,证明:取BC的中点D,连接AD.
∵AB=AC,BD=CD,AD=AD,
∴△ABD≌△ACD(SSS).∴∠B=∠C(全等三角形对应角相等)。教师与学生一起关注知识生成过程的数学课堂妙趣横生,培养了学生的自学能力,指引学生踏上了探究之旅。
三、开启思维之泉,拓展思维空间
关注生成的数学课堂发展思维,功不可没。如,在“相交线与平行线”时,教师出示了这样一道题:一条公路两次转弯之后,还和原来的方向相同(如图3),如果第一次拐的角是140°,那么第二次拐的角是多少度?为什么?学生一开始看到这道题,都觉得无从下手。稍作思考之后,学生甲提出:“两次转弯之后,还和原来的方向相同。”说明转弯之后的公路和原来的公路是平行的。其他同学马上想到了分别延长AB、DC(如图4),则:∵AB∥CD,∴∠ABC=∠BCD=140°(两直线平行,内错角相等),所以第二次拐的角仍然是140°。关注知识生成的数学课堂促使学生不断挖掘思维潜力,犹如点燃了学生的智慧之火。教师又出示了这样一道题:(如图5),AC∥ED,AB∥FD,∠A=62°,求∠EDF的度数。题目出示之后,每个学生都开动脑筋寻找“突破点”,学生甲质疑道:现在只知道∠A=62°,而∠A和∠EDF似乎没有什么直接关系呀?学生乙提出:不是还有AC∥ED,AB∥FD两个已知条件吗?是否可以利用平行线的性质呢?学生丙茅塞顿开:是呀!∵AB∥FD.∴∠A=∠CFD.(两直线平行,同位角相等)∵AC//ED.∴∠CFD=∠EDF.(两直线平行,内错角相等)∵∠A=∠62°.∴∠EDF=∠62°.学生甲又说:也可以这样做呀!∵AC∥ED.∴∠A=∠BED.(两直线平行,同位角相等)∵AB∥FD.∴∠BED=∠EDF.(两直线平行,内错角相等)∵∠A=∠62°.
∴∠EDF=∠62°.关注知识生成过程的数学课堂促使学生不断开动脑筋,好似开启了学生的思维之泉。
总之,在初中数学课堂中,教师要在知识的生成过程中多措并举激发学生学习的兴趣,还数学课堂奥妙无穷之美;要在知识的生成过程中千方百计鼓励学生自主探究,循数学课堂培养自学能力之根;要在知识的生成过程中想方设法挖掘学生的思维潜力,显数学课堂拓展思维能力之本。让学生深谙在数学课堂中要注重知识结论,但绝对不可轻视知识生成过程之理。
参考文献:
[1]曹海燕.在细节中提升数学课堂知识生成效果[J].中学课程资源,2015(3).
[2]黄国聪.如何重视数学知识的生成过程[J].理科爱好者(教育教学版),2013(5).
[3]王建苹.预设诚可贵,生成价更高:初中数学课堂教学中巧妙生成的实践研究[J].考试周刊,2013(15).

