激光诱导击穿光谱技术/多元二次非线性回归分析土壤中的铬元素
何秀文 陈添兵 姚明印 周华茂 胡慧琴 王彩虹 刘木华
(江西农业大学工学院, 江西省高校生物光电及应用重点实验室, 南昌 330045)
激光诱导击穿光谱技术/多元二次非线性回归分析土壤中的铬元素
何秀文 陈添兵 姚明印 周华茂 胡慧琴 王彩虹 刘木华*
(江西农业大学工学院, 江西省高校生物光电及应用重点实验室, 南昌 330045)
利用激光诱导击穿光谱(LIBS)技术对土壤中铬元素的含量进行了定量分析研究。由于土壤成分复杂,光谱谱线存在较严重的重叠干扰,若采用一元回归方法分析常得不到理想结果。为了更充分有效地利用光谱中信息,以土壤中Cr Ⅰ 425.43 nm和Fe Ⅰ 425.07 nm谱线的积分强度为自变量,Cr元素浓度为因变量,建立交叉降维近似多元非线性回归、多元二次非线性回归和平方降维近似多元非线性回归模型。对比分析表明,当添加Cr和Fe元素特征谱线强度交叉项影响时,所建立的多元二次非线性回归模型效果最佳,预测浓度与实际参考浓度之间线性关系达到0.9943,预测4个验证样品的相对误差分别为3.57%, 0.76%, 7.66%和2.24%。
激光诱导击穿光谱; 铬元素; 多元二次非线性; 定量分析
1 引 言
土壤是人类赖以生存的自然资源,与人体健康息息相关。然而随着工业的发展,土壤重金属污染已影响到了人们的健康生活,部分区域出现“镉大米”、“癌症村”和儿童血铅超标等情况,使得土壤重金属污染物的快速检测成为人们关注的焦点。激光诱导击穿光谱 (Laser-induced breakdown spectroscopy, LIBS) 是20世纪后期发展的一种对物质元素定性和定量分析的光谱技术,其原理是利用高功率脉冲激光聚焦后作用到待测样品,样品表面瞬间被气化,形成高温、高电子密度的等离子体,并用光纤光谱仪收集其等离子体光谱信号,通过对光谱数据分析可获得物质中所含元素种类及含量。由于其系统操作简单,无需复杂的样品预处理,固态、液态、气态均适用,能实现多元素同时检测,LIBS技术已被广泛应用于土壤重金属检测[1,2]、煤质分析[3,4]、冶金分析[5,6]、水溶液污染[7,8]、农产品质量安全[9]、气溶胶[10]等诸多领域。LIBS定量分析的依据是分析元素的特征光谱强度与其浓度之间存在某种关系,理想情况下待测元素浓度越高,其特征光谱强度越强,会形成一定的线性关系。然而由于激光诱导产生的等离子体演变过程十分复杂,其过程容易受到激光能量、样品的基质组成、样品的平整度、样品的烧蚀量及等离子体周边气体环境等等诸多因素的影响。所以,如果只是使用单一谱线强度对待测元素进行定标,会使得光谱中其它有效信息丢失,使得准确度不高。综上种种原因,导致目前LIBS技术检测准确性和重复性还不如原子吸收光谱(AAS)、电感耦合等离子体发射光谱等(ICP-OES)等常规的化学方法。
为了提高LIBS技术检测准确性和重复性,国内外研究者采用双脉冲激发等离子体、激光烧蚀等离子体及各种多元校正数据处理等方法改善LIBS技术检测能力。张谦等[11]采用光电双脉冲技术检测了水溶液中痕量汞元素,光电双脉冲LIBS技术与传统的单脉冲LIBS技术相比,汞元素在253.65 nm处原子辐射信号强度增强了约50倍,汞的检出限降低了一个数量级。Windom等[12]利用激光烧蚀激光诱导技术(LA-LIBS)分析了Cu, Al, Mg和Mn标准物质样品,提高了待测元素探测的灵敏度。邹孝恒等[13]采用LIBS技术建立了基于遗传算法( GA) 和偏最小二乘法( PLS)的定量分析模型对土壤成分进行检测。结果表明,GA作为一种谱线选择的预处理方法,可以有效减少用于PLS 建模的光谱谱线的数目,从而简化模型,并且GA-PLS模型能够显著改善传统PLS 模型的预测能力。Wang 等[14]利用基于偏最小二乘(PLS)法的非线性多变量主导因素模型对黄铜合金进行分析,预测标准差和标准误差分别为1.97%和1.05%,相关系数可达到0.999。Kwak等[15]提出内标元素定标法与自由定标法对土壤中的Pb元素进行分析。内标元素定标法要求样品中存在某种含量相对恒定的元素,然而对自然界未知成分样品分析时,无法保证内标元素含量的稳定。孙兰香等[16]基于LIBS技术采用一种多元二次非线性定标方法分析了多品种合金钢中锰(Mn)和硅(Si)的浓度,相比线性标准定标曲线法,测量结果的相对标准差从20%以上降低到10%以下,Mn元素测量结果的准确度提高了5倍多, Si元素提高了6倍多。陈兴龙等[17]基于内标方法和多谱线加权组合方法,建立了一种多元非线性定量分析模型分析钢铁中的Mn元素,对比结果表明,该多元非线性模型的测量准确性和重复性均优于单谱线内标模型。
本研究以国家标准土壤中铬元素为研究对象,选取Cr 425.43 nm和Fe 425.07 nm特征谱线积分强度作为模型的自变量,Cr浓度作为因变量,建立多元非线性回归模型,为考虑Cr元素和Fe元素的交叉相互影响因素,对多元非线性回归方程进行改进和比较,得出多元二次非线性回归效果较好,该模型的预测浓度与实际参考浓度之间线性关系达到0.9943,预测4个验证样品的相对误差分别为3.57%, 0.76%, 7.66%和2.24%。此模型不仅利用了Cr元素的特征谱线信息,还考虑了土壤基体元素Fe对Cr谱线产生的共存效应。
2 实验系统
图1为LIBS实验系统装置示意图,实验采用的光源是Nd∶YAG 激光器,波长为1064 nm,单脉冲最大能量为200 mJ,脉冲宽度为8 ns,重复频率设在2 Hz。
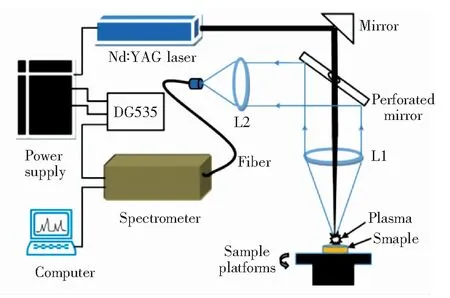
图1 LIBS实验系统装置原理图Fig.1 Schematic diagram of the experimental setup
激光束经过100 mm的透镜聚焦在土壤样品表面,产生的激光等离子体信号经焦距为100 mm 的石英透镜耦合至光纤,传输到光谱仪完成光谱的分光与探测,其中光谱仪是荷兰爱万提斯公司生产的AvaSpec-2048型八通道光纤光谱仪,其响应波长为200~1050 nm,分辨率为0.06~0.13,探测光谱信号采用的是像素为2048的CCD相机。在实验过程中,土壤样品被放置在SC300-1A型三维调节电控精密平移台(卓立汉光公司)上,设置其匀速旋转运动,以保证激光作用于样品表面的不同点上。激光器和光谱仪均采用外触发工作模式,由DG535数字脉冲延时器控制二者之间光谱信号采集的同步延迟时间。

图2 土壤在424~430 nm波段内的激光等离子体光谱Fig.2 Laser induced breakdown spectrometric (LIBS) spectrum of soil sample at 420-430 nm
3 实验方法及分析
3.1 样品制备与特征谱线的分析
实验样品为国家标准物质土壤样品GBW7401, GBW7402, GBW7403, GBW7404, GBW7405, GBW7406和GBW7408(中国计量科学院),利用这7个标准样品按一定比例配制9个混合样品,共16个样品(1~16#),为了使配制的土壤混合均匀,将样品置于匀速振荡器里振荡5 min,并用手动压片机对样品进行压片制样(压力为20 MPa),每个样品制成直径为30 mm,厚度为5 mm的圆饼块状型,16个样品的铬含量如表1所示。其中1~12#为定标样品,13~16#为验证样品。如图2所示, 实验记录土壤样品(GBW7404)在424~430 nm的激光等
表1 16个土壤样品中铬的含量
Table 1 Cr concentrations of sixteen soil samples

样品SampleCr含量Content(μg/g)1#62.02#68.03#73.24#75.05#78.06#84.47#88.08#92.2样品SampleCr含量Content(μg/g)9#109.410#249.211#252.012#370.013#83.614#100.815#118.016#246.8
离子体发射光谱。实验所用的激光能量为100 mJ,重复频率为2 Hz;光谱仪采集延时为1.4 μs,积分时间为2 ms。为了提高光谱信噪比,每个样品采集10幅光谱,每幅光谱由20个脉冲累加组成。根据美国国家标准与技术研究院(NIST)的原子发射光谱数据库可知,Cr在420~430 nm之间有三重线Cr Ⅰ 425.43 nm,Cr Ⅰ 427.48 nm,Cr Ⅰ 428.97 nm。
由于土壤中Fe元素含量较高,是土壤中的基体元素,且谱线丰富,在424~430 nm波段内有Fe Ⅰ 425.07 nm, Fe Ⅰ 426.04 nm, Fe Ⅰ 427.17 nm,Fe Ⅰ 428.28 nm,所以Fe元素的发射谱线强度可对Cr的定量分析产生较大影响,其中Cr的原子谱线Cr Ⅰ 427.48 nm和428.97 nm受到Fe元素和Ti元素的干扰较大,而Cr Ⅰ 425.43 nm谱线受到干扰较小,谱线清晰。因此选择Cr Ⅰ 425.43 nm谱线作为分析线,并且由于Fe Ⅰ 425.07 nm谱线与分析线相邻最近,对分析线产生干扰,所以本实验以土壤中Cr Ⅰ 425.43 nm谱线强度和Fe Ⅰ 425.07 nm谱线强度为自变量,Cr元素浓度为因变量,进行多元变量定量分析。
3.2 多元二次非线性定标及分析
多元回归方法是基于化学计量学的一种常规的定量分析方法,具有较好的统计特性。在LIBS系统中,由于光谱谱线会存在不同程度的自吸收及元素之间共存效应,破坏了原有的线性关系,这时采用多元非线性回归定标能同时利用多条光谱信息,更好地描述谱线强度与分析元素浓度之间的关系。
假设用于定标的样品数为n, 观察的波长数为m, 需要测量的组分数为p, 对于某元素j的浓度与光谱强度间的多元二次非线性模型为[18]
(1)
式中[Cj]为元素j(n=1,2,…p)的浓度向量,维数为n;bi,j为多元非线性回归方程系数;[Ii]为光谱线(i=1,2, …,m)的强度向量,维数为n;[ej]为服从正态分布的随机误差向量,维数为n。
以土壤中Cr Ⅰ 425.43 nm谱线强度和Fe Ⅰ 425.07 nm谱线强度为自变量,Cr元素浓度为因变量,根据式(1)进行多元二阶非线性拟合,则Cr元素的浓度如式(2):
(2)
式中,b0~ b4为多元非线性回归方程的系数,CCr, ICr和IFe分别代表Cr元素浓度、CrⅠ 425.43nm谱线强度和FeⅠ 425.07nm谱线强度。利用12个定标样品和4个验证样品,根据式(2)函数关系得到的测量结果如图3所示。

图3 铬元素的交叉降维近似多元非线性拟合Fig.3 Calibration curve of Cr with cross dimension reduction in binary quadric terms

(3)

(4)
式(4)的这种函数关系称为平方降维近似多元非线性回归[19],其测量结果如图5所示。由图5可知,其模型的回归效果不及图4。表2列出了采用交叉降维近似多元非线性回归、多元二次非线性回归和平方降维近似多元非线性回归算法对待测土壤样品中Cr元素定量分析的结果。

图4 多元二次非线性回归拟合Fig.4 Calibration curve of Cr with multiple in binary quadric terms

图5 平方降维近似多元非线性拟合Fig.5 Calibration curve of Cr with square dimensionreduction in binary quadric terms
表2 不同多元非线性回归定标方法对4个待测样品中 Cr含量的分析结果
Table 2 Results of Cr content for four test sample with different multiple quadratic non-linear regression

样品Sample参考值Certificatedvalue(μg/g)MethodⅠ预测值Predictedvalues(μg/g)相对误差Relativeerror(%)MethodⅡ预测值Predictedvalues(μg/g)相对误差Relativeerror(%)MethodⅢ预测值Predictedvalues(μg/g)相对误差Relativeerror(%)13#83.6084.010.4980.623.5792.3610.4814#100.8063.2337.27100.030.7696.044.7215#118.0062.4647.06108.967.6694.7419.7116#246.80274.9411.40252.332.24269.659.26MethodⅠ:交叉降维近似多元非线性(Crossdimensionreductioninbinaryquadricterms);MethodⅡ:多元二次非线性(Multipleinbinaryquadricterms);Ⅲ.平方降维近似多元非线性(Squaredimensionreductioninbinaryquadricterms)。
比较交叉降维近似多元非线性和多元二次非线性定标方法可知,土壤中Cr Ⅰ 425.43 nm和Fe Ⅰ 425.07 nm谱线强度交叉项对测量Cr元素含量的测量影响较大;而比较多元二次非线性和平方降维近似多元非线性回归方法可知,在多元二次非线性回归拟合中,虽然交叉项的贡献率比较大,但也不能忽略贡献相对小的平方项。因此,在采用多元非线性回归定标方法分析土壤中Cr元素含量时,应该考虑将Cr和Fe元素谱线强度交叉项添加到回归拟合中,回归模型质量最佳,模型对待测样品反演计算出的结果的相对误差也最小,均在10%以内。
4 结 论
基于LIBS技术对土壤中Cr元素的含量进行了定量分析,选出了Cr Ⅰ 425.43 nm和Fe Ⅰ 425.07 nm两条特征谱线强度作为多元非线性定标的自变量,土壤中Cr含量为因变量。从考虑Cr和Fe元素谱线强度的交叉影响出发,分别对比研究了交叉降维近似多元非线性回归、多元二次非线性回归和平方降维近似多元非线性回归三种定标方法对土壤中Cr含量的测量结果。从回归分析中得出,Cr和Fe元素谱线强度的交叉项的贡献率较大,并且添加了交叉项所建立的多元二次非线性回归模型的质量最好,模型预测浓度与实际参考浓度之间线性关系达到0.9943,4个待测样品的测量相对误差也明显低于其它两种多元非线性回归方法。说明本研究提出的多元二次非线性函数关系式适合土壤中Cr元素的LIBS定量分析,为在复杂基体效应下微量甚至痕量元素的在线快速检测提供一种新的途径。
1 LU Cui-Ping, LIU Wen-Qing, ZHAO Nan-Jing, LIU Li-Tuo, CHEN Dong, ZHANG Yu-Jun, LIU Jian-Guo.ActaPhys.Sin., 2011,60(4): 388-392
鲁翠萍, 刘文清, 赵南京, 刘立拓, 陈 东, 张玉钧, 刘建国. 物理学报, 2011, 60(4): 388-392
2 DU Chuang, GAO Xun, SHAO Yan, SONG Xiao-Wei, ZHAO Zhen-Ming, HAO Zuo-Qiang, LIN Jing-Quan.ActaPhys.Sin., 2013, 62(4): 045202
杜 闯, 高 勋, 邵 妍, 宋晓伟, 赵振明, 郝作强, 林景全. 物理学报, 2013, 62(4): 045202
3 YAO Shun-Chun, LU Ji-Dong, PAN Sheng-Hua, JIANG Mei-Cheng, XIE Cheng-Li, LI Jie, LI Pin.ProceedingsoftheCSEE, 2009, 29(23): 80-83
姚顺春, 陆继东, 潘圣华, 蒋梅城, 谢承利, 李 捷, 李 娉. 中国电机工程学报, 2009, 29(23): 80-83
4 YIN Wang-Bao, ZHANG Lei, ZHANG Jian-Hong, WANG Le, HU Zhi-Yu, JIA Suo-Tang.JournalofTestingTechnology, 2011, 25(4): 356-359
尹王保, 张 雷, 张建宏, 王 乐, 胡志裕, 贾锁堂. 测试技术学报, 2011, 25(4): 356-359
5 SUN Lan-Xiang, YU Hai-Bin, CONG Zhi-Bo, XIN Yong.ActaOpticaSinica, 2010, 30(09): 2757-2765
孙兰香, 于海斌, 丛智博, 辛 勇. 光学学报, 2010, 30(09): 2757-2765
6 CUI Zhi-Feng, ZHANG Xian-Yan, YAO Guan-Xin, WANG Xiao-Li, XU Xin-Shen, ZHENG Xian-Feng, FENG Er-Yin, JI Xue-Han.ActaPhys.Sin., 2006, 55(09): 4506-4513
崔执凤, 张先燚, 姚关心, 汪小丽, 许新胜, 郑贤锋, 凤尔银, 季学韩. 物理学报, 2006, 55(09): 4506-4513
7 CHANG Liang, LIN Zhao-Xiang, LI Jie, LIU Lin-Mei, LIU Ye-Lin.HighPowerLaserandParticleBeams, 2010, 22(6): 1369-1372
常 亮, 林兆祥, 李 捷, 刘林美, 刘业林. 强激光与粒子束, 2010, 22(6): 1369-1372
8 ZHAO Fang, ZHANG Qian, XIONG Wei, RONG Jing-Bao, LI Run-Hua.EnvironmentalScience&Technology, 2010, 33(3): 137-140
赵 芳, 张 谦, 熊 威, 容静宝, 李润华. 环境科学与技术, 2010, 33(3): 137-140
9 CHEN Tian-Bing, YAO Ming-Yin, LIU Mu-Hua, LIN Yong-Zeng, LI Wen-Bing, ZHENG Mei-Lan, ZHAO Hua-Mao.ActaPhys.Sin., 2014, 63(10): 104213
陈添兵, 姚明印, 刘木华, 林永增, 黎文兵, 郑美兰, 周华茂. 物理学报, 2014, 63(10): 104213
10 Mc Naghten E D, Parkes A M, Griffiths B C.SpectrochimicaActa.PartB:AtomicSpectroscopy, 2009, 64(10): 1111-1118
11 ZHANG Qian, XIONG Wei, CHEN Yu-Qi, LI Run-Hua.SpectroscopyandSpectralAnalysis, 2011, 31(02): 521-524
张 谦, 熊威, 陈钰琦, 李润华. 光谱学与光谱分析, 2011, 31(02): 521-524
12 Windom B C, Hahn D W.J.Anal.At.Spectrom, 2009, 12(24):1665-1675
13 ZOU Xiao-Heng, HAO Zhong-Qi, YI Rong-Xing, GUO Lian-Bo, SHEN Meng, LI Xiang-You, WANG Ze-Min, ZENG Xiao-Yan, LU Yong-Feng.ChineseJ.Anal.Chem., 2015, 43(3): 181-186
邹孝恒, 郝中骐, 易荣兴, 郭连波, 沈 萌, 李祥友, 王泽敏, 曾晓雁, 陆永枫. 分析化学, 2015, 43(3): 181-186
14 Wang Z, Feng J, Li L.JournalofAnalyticalAtomicSpectrometry, 2011, 26(11): 2175-2182
15 Kwak J, Kim K W, Park M, Kim J, Park K.EnvironmentalTechnology, 2012, 33(18): 2177-2184
16 SUN Lan-Xiang, YU Hai-Bin, XIN Yong, CONG Zhi-Bo.SpectroscopyandSpectralAnalysis, 2010, 30(12): 3186-3190
孙兰香, 于海斌, 辛 勇, 丛智博. 光谱学与光谱分析, 2010, 30(12): 3186-3190
17 CHEN Xing-Long, FU Hong-Bo, WANG Jing-Ge, NI Zhi-Bo, HE Wen-Gan, XU Jun, RAO Rui-Zhong, DONG Feng-Zhong.SpectroscopyandSpectralAnalysis, 2014, 34(11): 3100-3103
陈兴龙, 付洪波, 王静鸽, 倪志波, 贺文干, 徐 骏, 饶瑞中, 董凤忠. 光谱学与光谱分析, 2014, 34(11): 3100-3103
18 Laville S, Sabsabi M, Doucet F R.SpectrochimicaActaPartB, 2007, 62(12): 1557-1566
19 LI Yin. Ph. D. Dissertation (Qingdao: Ocean University of China ), 2011: 60-76
李 颖. 博士学位论文(青岛: 中国海洋大学), 2011: 60-76
(Received 19 June 2015; accepted 11 August 2015)
This work was supported by the National Natural Science Foundation of China (No. 31460419), the Science and Technology Plan Projects of Jiangxi Province, China (No. 20143ACB21013) the Key Science and Technology Program of Jiangxi Province, China (No. CJJ12249), and the Jiangxi Province Foundation for Leaders of Disciplines in Science, China (No.09004004)
Quantitative Analysis of Chrome in Soil Based on Multiple Quadratic Non-linear Regression Model by Laser-Induced Breakdown Spectroscopy
HE Xiu-Wen, CHEN Tian-Bing, YAO Ming-Yin, ZHOU Hua-Mao, HU Hui-Qin, WANG Cai-Hong, LIU Mu-Hua*
(KeyLaboratoryofOptics-ElectricsApplicationofBiomaterialsofJiangxiProvince,CollegeofEngineering,JiangxiAgriculturalUniversity,Nanchang330045,China)
The chrome concentration in soil was quantitatively analyzed by laser induced breakdown spectroscopy (LIBS). Due to the complexity of soil components, there is serious overlap interference spectral line, which leads to the unsatisfactory results for the monadic regression analysis. To obtain the more effective spectrum information, by using the spectral intensity of Cr Ⅰ 425.43 nm and Fe Ⅰ 425.07 nm as independent variables and Cr concentration as dependent variable, the methods of cross dimension reduction approximate multivariate nonlinear regression, multiple quadratic non-linear regression and square dimension reduction approximate multivariate nonlinear regression were established. The results showed that when the cross term for characteristic spectral intensity of Cr Ⅰ 425.43 nm and Fe Ⅰ 425.07 nm was used, the multiple quadratic nonlinear regression model was better than others. The correlation coefficients between predicted concentration and reference concentration reached 0.9943, and the relative error of four predicted sample was 3.57%, 0.76%, 7.66% and 2.24% respectively.
Laser induced breakdown spectroscopy; Chrome; Multiple quadratic nonlinear regression; Quantitative analysis
10.11895/j.issn.0253-3820.150501
本文系国家自然科学基金 (31460419)、江西省科技计划项目(20143ACB21013)、江西省教育厅科技计划 (CJJ12249) 和江西省学术带头人计划 (09004004) 资助
2015-06-19收稿;2015-08-11接受
* E-mail: suikelmh@sohu.com

