有机物在水中溶解度范数指数法定量构效关系
崔 雪,贾青竹,李 磊,王 强
(1. 天津科技大学海洋与环境学院,天津 300457;2. 天津科技大学化工与材料学院,天津 300457)
有机物在水中溶解度范数指数法定量构效关系
崔 雪1,贾青竹1,李 磊2,王 强2
(1. 天津科技大学海洋与环境学院,天津 300457;2. 天津科技大学化工与材料学院,天津 300457)
有机物溶解度参数在化学品开发、药物设计和环境生态保护评价等领域发挥重要作用.本文依据本课题组提出的范数指数描述符,建立了一个预测有机物溶解度的定量构效关系模型,并对320个包括有机氯化物、烷基类、芳香族等有机物的水溶解度进行了计算.留一交叉验证和 Y随机化测试表明这个新计算模型预测结果精确、可靠和稳定(R2为0.910,7,Q2为0.888,4);同时,该模型的应用域验证结果表明此模型有可能在大范围上推广运用.模型统计结果和相关验证结果都表明基于范数指数建立的定量构效关系模型可以成功应用于预测有机物溶解度.
有机物溶解度;范数指数;定量构效关系;留一交叉验证;应用域
有机物在水中的溶解度(mol/L,通常表示为对数形式即 log,S)属于基础理化性质,该参数在化学品开发、药物设计和环境生态保护评价等领域发挥重要作用[1].其中,在药物设计领域,溶解度参数与吸收、分布、新陈代谢、代谢和毒性有关[2];比如有机物的超低溶解度有可能带来药物吸收问题[3],尽管提高摄入药剂量能达到预期治疗效果,但由此可导致更严重的药物中毒问题.随着高通量筛选技术和结构化学的发展,大量候选药物分子被设计成大分子质量、低溶解度和高脂溶性[4].据统计,每年新开发上市的化学品达2,000种以上;同时,为了实现对化学品在生产、流通、使用及最终处置归宿过程中的规范管理,欧盟要求所有化学品在正式市场化生产之前,就应该提供包括辛醇水分配系数、水溶解度及吸收、分布、新陈代谢、代谢和毒性等相关参数[5].因此,在有机物溶解度实验测量耗时费力情况下,要快速排除超低溶解度的候选药物分子,提高药物开发效率,有效解决途径就是建立稳定准确的有机物溶解度预测模型.
定量构效关系是一个基于大量描述符将化合物结构与其物性参数(溶解度)定量联系起来的方法[6-13].例如,Hansen等[10]利用9个2D描述符建立了一个人工神经网络模型,对4,548个类药物分子的溶解度参数进行了估算,尽管计算结果精度较高,但是该人工神经网络系统属于暗箱模型,不能进一步推广应用.根据 9个潜在描述符(包括扩展的连接性指纹分数),Zhou等[11]建立了偏最小二乘法的模型,并对 1,302个有机物进行了预测,结果表明其测试集(1,000个有机物)计算相关系数(R2)为 0.85,均方根误差为0.71.有研究者[12]基于3D描述符分别采用反向传播神经网络和多元线性回归两种拟合过程建立了有机物溶解度预测模型,研究表明前者方法能给出较好计算精度.
本课题组提出系列范数指数描述符,基于该描述符建立的模型成功地预测了有机物多种物化性质,包括离子液体的分解温度、麻醉性污染物的水生毒性、杂环化合物的药理学和毒理学活性和多种类表面活性剂的临界胶束浓度[14-17].先前研究工作表明该系列范数描述符可能是分子结构的一种根本表述,有可能在多个物性参数中均有体现.
本工作基于有机物分子图论进一步将欧式空间距离矩阵引入到范数模式中,并据此建立有机物的溶解度预测模型,对 320个有机物包括有机卤化物(Cl和 Br)、烷烃类、烯烃类、炔烃类、醇类、芳香族等极性和非极性有机物的水溶解度进行了计算,采用留一交叉验证法和 Y随机化验证手段对模型进行了验证,并利用杠杆技术对模型的应用域进行了评价.
1 研究方法
1.1样本集
在此工作中,包含溶解度数据有机物分子从文献[13]中获得,其溶解度实验值(log,S)及分子结构列在附表 1(可联系通信作者索取).对实验数据进行了可靠性评价,对明显异常数据进行剔除,对同一个有机物的多个实验数据进行了再次核实,筛选确定了 320个有机物.为了构建稳定准确的计算模型,将样本集分为训练集(260个有机物)和测试集(60个有机物).
1.2分子结构优化
利用软件 HyperChem 7.0对有机物分子结构进行优化,具体采用从头算法ab initio在ST0-3G中进行能量最低优化.
1.3范数指数描述符和模型
在分子结构优化基础上,利用化学图构建有机物的距离矩阵和欧式空间距离矩阵.其中,距离矩阵包括了步长矩阵、相邻矩阵、相间矩阵和相跳矩阵.为了对分子中的不同原子进行量化描述,本工作提出了增广矩阵,涉及参数包括范德华半径、原子质量、电负性和电荷.
下面列出上述具体矩阵.
欧式空间距离矩阵:

bij是原子i和j的欧氏空间距离步长矩阵:

相邻矩阵:

相间矩阵:

相跳矩阵:

增广矩阵:

将以上矩阵进行组合,形成新矩阵,命名为增广距离矩阵.
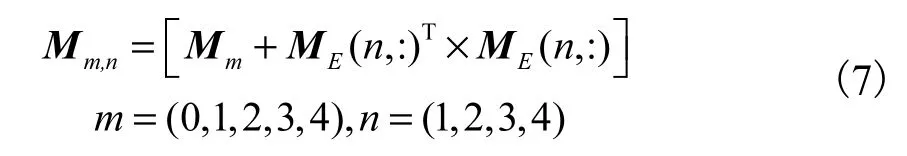


表1 溶解度预测模型系数Tab.1 Parameters of this model for solubility prediction
1.4模型评价
预测模型质量高低通过回归统计数值、留一交叉验证法和 Y随机化进行验证.回归统计数据包含训练集和测试集相关系数的平方值,留一交叉验证法的统计数据是Q2.
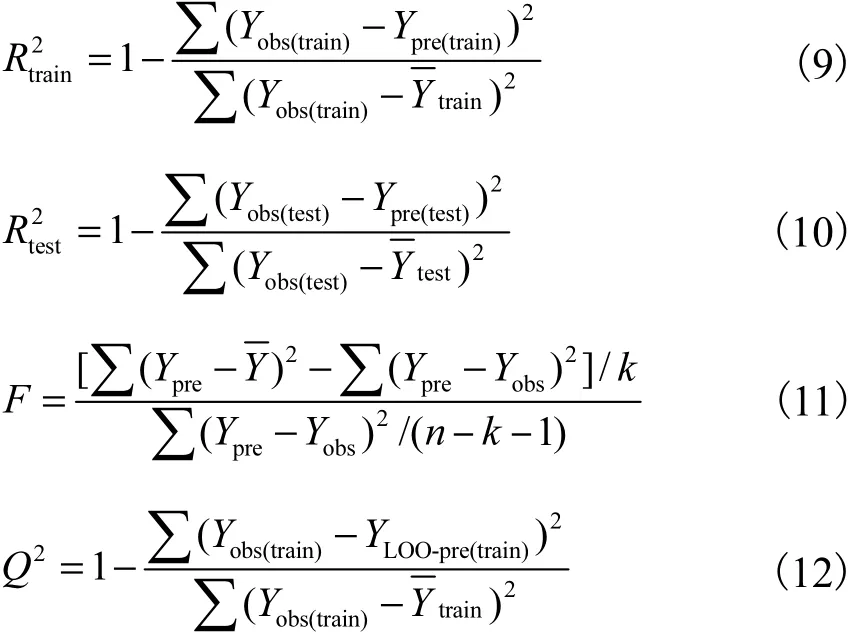
式中:Yobs(train)为训练集实验值;Ypre(train)为训练集预测值;train为训练集实验值的平均值;Yobs(test)为测试集实验值;Ypre(test)为测试集预测值;test为测试集实验值的平均值;Yobs为样本集实验值;Ypre为样本集预测值;n为样本集数量;k为变量数量;为样本集实验值的平均值;YLOO-pre为样本集留一交叉验证的预测值.
1.5应用域验证
为了遵守欧盟 OECD原则,定量构效关系模型的应用域应该给出明确定义.本工作以分子结构的帽子矩阵为基础,通过杠杆方法来确定计算模型的应用域.比如由于某有机物的杠杆值比较高该有机物的预测值就可能被认为是不可靠的.其中h*的定义为

式中:p'是自变量数量加1;n是训练集数量.
为了方便可视化本模型的应用域,使用了Williams图(标准交叉验证残差为纵坐标,有机物的杠杆值为横坐标).有机物的标准交叉验证残差处于三个标准残差单位内(<3σ)且h<h*,则认定为该有机物的预测结果是可靠的;否则,该有机物的预测值被认定为是异常值[18-19].
2 结果与讨论
2.1溶解度的定量构效关系模型
利用新建模型(式(8))对320个有机物的溶解度进行了预测,具体预测数值见附表 1,图 1是有机物溶解度实验值与预测值对比散点图.由图1可知:所有有机物溶解度预测点和实验点均位于对角线上及附近,表明本模型计算结果与实验值有很好的一致性.本预测模型相关统计数据和F值分别为 0.910,7、0.890,1和 327.14,说明本模型计算结果的精确性较好.同时,图 2表明几乎所有有机物的溶解度预测残差都分布在-2到+2之间,残差随机分布没有明显趋势.

图1 溶解度预测值和实验值相关性Fig.1 Correlation between model predicted and experimental data

图2 残差与实验值对比图Fig.2 Model predicted residual vs.experimental data
2.2留一交叉验证
本文利用留一交叉验证法验证本计算模型的预测能力.留一交叉验证法所建立模型的预测值和实验值之间关系对比图如图3所示.图3表明:留一交叉验证法的溶解度预测值与实验值有较好吻合度.为了进一步分析本工作模型(式(8))和留一交叉验证生成模型的溶解度预测效果,对比了两种模型预测结果样本的相对误差分布情况,结果如图4所示.
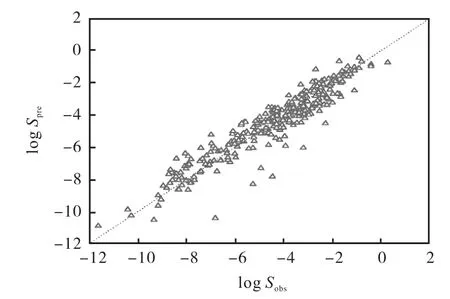
图3 留一交叉验证预测值和实验值相关性Fig.3 Correlation between leave-one-out cross-validation predicted and experimental data
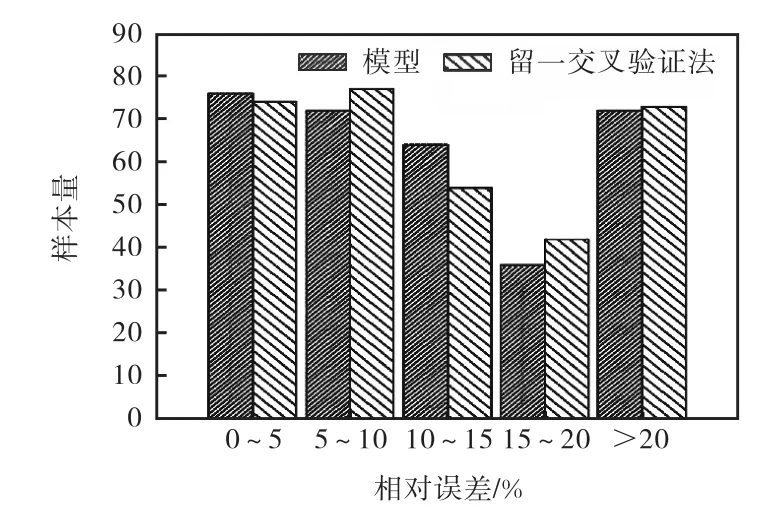
图4 本模型和留一交叉验证模型溶解度预测相对偏差分布Fig.4 Relative deviation distribution of the solubility predicted by this model and the leave-one-out cross-validation model
由图4可知,二者预测结果的相对误差数量分布相似.同时,留一交叉验证结果具有较高Q2值(0.888,4),以上表征结果均可以验证本工作基于范数描述符建立的溶解度预测模型具有较好的稳定性和可靠性.
2.3Y随机化测试
为了避免模型建立的偶然性,需要对模型进行Y随机化测试.将原始实验值Y随机打乱顺序几次,同时运用相同的变量再建立一个新的定量构效关系模型;如果新模型预测结果R2和Q2都很低,则可以证明原始模型不是偶然建立的,同时具有较强稳定性.
在本工作中,实验值被随机打乱了 5次顺序,其随机打乱生成新模型预测结果的R2和Q2列在表2.由表2可知:5次 Y随机化测试中新模型的预测效果都很差,R2和Q2都很低甚至为 0;由此推断,本工作原始模型(式(8))是稳固的,并非偶然建立.

表2 Y随机化测试结果Tab.2 Results of the randomization test of the model
2.4应用域验证
好的计算模型不仅要有较高的精确度和稳定性,同时要具备较广的应用域.本工作利用杠杆方法检测计算模型的应用域,并由 Williams图(见图 5)展示,其中图 5横纵坐标是帽子矩阵对角线的数值分布,纵坐标是预测结果标准残差分布.从图 5可以看出,对于320个有机物,只有7个有机物的预测结果属于异常值,其中 98%, 的样本有机物预测结果都稳定可靠.由此推断本计算模型(式(8))具有较广应用域,可以推广应用于其他有机物溶解度的预测.

图5 训练集和测试集Williams图Fig.5 Williams plot for the training set and the test set
3 结 语
本文基于有机物化学图论,构造了有机物分子的欧式空间距离矩阵、步长矩阵和原子属性矩阵,在此基础上提出了系列组合矩阵的范数指数,构建了有机物溶解度预测定量构效关系模型,并对320个包括有机氯化物、烷基类、芳香族等有机物的水溶解度进行了计算.结果表明:本模型溶解度预测值与实验值有很好的一致性,F值为 327.14,留一交叉验证测试(Q2为 0.888,4)、Y随机化测试和应用域验证均表明本模型计算结果准确稳定可靠,有可能进一步推广应用.
[1] Mitchell B E,Jurs P C. Prediction of aqueous solubility of organic compounds from molecular structure[J]. Journal of Chemical Information and Computer Sciences,1998,38(3):489-496.
[2] Tetko I V,Bruneau P,Mewes H W,et al. Can we estimate the accuracy of ADME-Tox predictions?[J]. Drug Discovery Today,2006,11(15):700-707.
[3] Lipinski C A,Lombardo F,Dominy B W,et al. Experimental and computational approaches to estimate solubility and permeability in drug discovery and development settings[J]. Advanced Drug Delivery Reviews,2012,64:4-17.
[4] Votano J R,Parham M,Hall L H,et al. New predictors for several ADME/Tox properties:Aqueous solubility,human oral absorption,and Ames genotoxicity using topological descriptors[J]. Molecular diversity,2004,8(4):379-391.
[5] Wang J,Hou T. Recent advances on aqueous solubility prediction[J]. Combinatorial Chemistry & High Throughput Screening,2011,14(5):328-338.
[6] Delaney J S. Predicting aqueous solubility from structure[J]. Drug Discovery Today,2005,10(4):289-295.
[7] Jain N,Yalkowsky S H. Estimation of the aqueous solubility I:Application to organic nonelectrolytes[J]. Journal of Pharmaceutical Sciences,2001,90(2):234-252.
[8] Hou T J,Xia K,Zhang W,et al. ADME evaluation in drug discovery. 4. Prediction of aqueous solubility based on atom contribution approach[J]. Journal of Chemical Information and Computer Sciences,2004,44(1):266-275.
[9] Tetko I V,Tanchuk V Y,Kasheva T N,et al. Estimation of aqueous solubility of chemical compounds using E-state indices[J]. Journal of Chemical Information and Computer Sciences,2001,41(6):1488-1493.
[10] Hansen N T,Kouskoumvekaki I,Jørgensen F S,et al. Prediction of pH-dependent aqueous solubility of druglike molecules[J]. Journal of Chemical Information and Modeling,2006,46(6):2601-2609.
[11] Zhou D,Alelyunas Y,Liu R. Scores of extended connectivity fingerprint as descriptors in QSPR study of melting point and aqueous solubility[J]. Journal of Chemical Information and Modeling,2008,48(5):981-987.
[12] Yan A,Gasteiger J. Prediction of aqueous solubility of organic compounds based on a 3D structure representation[J]. Journal of Chemical Information and Computer Sciences,2003,43(2):429-434.
[13] Wang J,Krudy G,Hou T,et al. Development of reliable aqueous solubility models and their application in druglike analysis[J]. Journal of Chemical Information and Modeling,2007,47(4):1395-1404.
[14] Zhu Z C,Wang Q,Jia Q Z,et al. Quantitative structureproperty relationship of the critical micelle concentration of different classes of surfactants[J]. Acta Physico-Chimica Sinica,2013,29(1):30-34.
[15] Zhu Z C,Wang Q,Jia Q Z,et al. Structure-property relationship for the pharmacological and toxicological activity of heterocyclic compounds[J]. Acta Physico-Chimica Sinica,2014,30(6):1086-1090.
[16] Yan F Y,Xia S Q,Wang Q,et al. Predicting the decomposition temperature of ionic liquids by the quantitative structure-property relationship method using a new topological index[J]. Journal of Chemical & Engineering Data,2012,57(3):805-810.
[17] Wang Q,Jia Q Z,Yan L H,et al. Quantitative structuretoxicity relationship of the aquatic toxicity for various narcotic pollutants using the norm indexes[J]. Chemosphere,2014,108:383-387.
[18] Gramatica P. Principles of QSAR models validation:Internal and external[J]. QSAR and Combinatorial Science,2007,26(5):694-701.
[19] Gramatica P,Giani E,Papa E. Statistical external validation and consensus modeling:A QSPR case study for Kocprediction[J]. Journal of Molecular Graphics and Modelling,2007,25(6):755-766.
责任编辑:周建军
A Quantitative Structure-property Relationship Model for Aqueous Solubility of Organic Compounds Based on Norm Indexes
CUI Xue1,JIA Qingzhu1,LI Lei2,WANG Qiang2
(1.College of Marine and Environmental Sciences,Tianjin University of Science & Technology,Tianjin 300457,China;2.College of Chemical Engineering and Materials Science,Tianjin University of Science & Technology,Tianjin 300457,China)
The aqueous solubility of organic compounds plays a significant role in chemical development,drug design and environmental protection evaluation.In this research,norm index descriptors were obtained and then utilized to develop a model for predicting the aqueous solubility of 320 organic compounds including organic chloride,alkyl and aromatic,etc.The model was validated by leave-one-out validation and Y-randomization test with satisfactory results(R2of 0.910,7,Q2of 0.888,4),which further demonstrated that this model was accurate,reliable and stable.Besides,the applicability domain of the model was validated by using the leverage approach and the results suggested a potential for a large scale utilization of this model.Statistical values and validation tests demonstrate that our norm indexes-based model can successfully predict the aqueous solubility of organic compounds.
aqueous solubility of organic compounds;norm indexes;quantitative structure-property relationship;leaveone-out cross-validation;applicability domain
O621.1
A
1672-6510(2016)04-0035-05
10.13364/j.issn.1672-6510.20150184
2015-10-28;
2015-12-16
国家自然科学基金资助项目(21306137)
崔 雪(1990-),女,天津人,硕士研究生;通信作者:贾青竹,教授,jiaqingzhu88@126.com.
数字出版日期:2016-05-19;数字出版网址:http://www.cnki.net/kcms/detail/12.1355.N.20160519.1023.002.html.

