方形同轴组合密封的结构及运行参数优化研究
张付英,孙宇佳,姜向敏
(天津市轻工与食品工程机械装备集成设计与在线监控重点实验室,天津科技大学机械工程学院,天津 300222)
方形同轴组合密封的结构及运行参数优化研究
张付英,孙宇佳,姜向敏
(天津市轻工与食品工程机械装备集成设计与在线监控重点实验室,天津科技大学机械工程学院,天津 300222)
利用 ANSYS分析了方形同轴组合密封的结构及运行参数对其动静态密封性能的影响.结果表明:主密封面的最大静态接触压力随着滑环厚度的增加而显著减小,随滑环两侧倒角或O形圈压缩率的增加而增大;活塞杆的往复运动速度和滑环的摩擦因数对主密封面的最大动态接触压力和密封面间的摩擦力影响不明显.应用响应曲面法,以得到密封面最大接触压力和最小摩擦力作为优化目标,对该组合密封的结构参数进行优化设计,得到了方形同轴组合密封的最佳参数组合方案,即当方形同轴密封的滑环厚度为2.03,mm、顶倒角角度为33.26°、O形圈压缩率为16.70%,时密封性能最优.
方形同轴组合密封;有限元分析;参数优化;响应曲面法
同轴组合密封由橡胶 O形圈和滑环组成.由于滑环材料(如聚四氟乙烯PTFE)的低摩擦因数和自润滑性可减小主密封面的摩擦力,使其在往复密封中得到广泛应用[1].格莱圈和斯特封是同轴组合密封的两种主要结构型式,其结构及运行参数直接影响组合密封的密封性能.谭晶等[2]对方形同轴密封件(格莱圈)的滑环厚度对接触压力及液体压力对密封圈变形的影响进行了分析.陈国栋[3]对阶梯型同轴密封件(斯特封)在工作压力、预压缩量以及结构参数方面对密封性能的影响进行了研究,并应用ANSYS提供的零阶优化方法,在滑环厚度及压缩率一定的前提下进行优化,得到了唇前角α、唇后角β及唇口偏移量R的最优解.然而,目前对于方形同轴组合密封件的倒角角度、滑环与活塞杆的接触宽度(以改变滑环顶倒角角度进行控制)、活塞杆运行速度、摩擦因数以及多因子在多个优化目标下的优化研究尚少.
本文通过对方形同轴组合密封的几何尺寸(滑环厚度、倒角角度、滑环与活塞杆的接触宽度)以及橡胶 O形圈的压缩率的变化分析格莱圈的静态密封性能;通过改变活塞杆往复运动速度和滑环摩擦因数研究格莱圈的动态密封性能.最后应用响应曲面法对方形同轴组合密封进行参数优化设计,为组合密封件的选用提供理论依据.
1 结构参数对方形同轴组合密封的静态密封性能影响
方形同轴组合密封的结构如图1所示.O形圈的尺寸为φ 44,mm×3.55,mm(GB 3452.1—1992),其压缩率为12%,;滑环厚度h=2.0,mm,滑环的两侧顶倒角α=60°,α1为滑环的两侧底倒角,活塞杆直径为40,mm,沟槽宽度为 4.2,mm,沟槽深度为 4.5,mm;L为滑环与活塞杆的接触宽度.
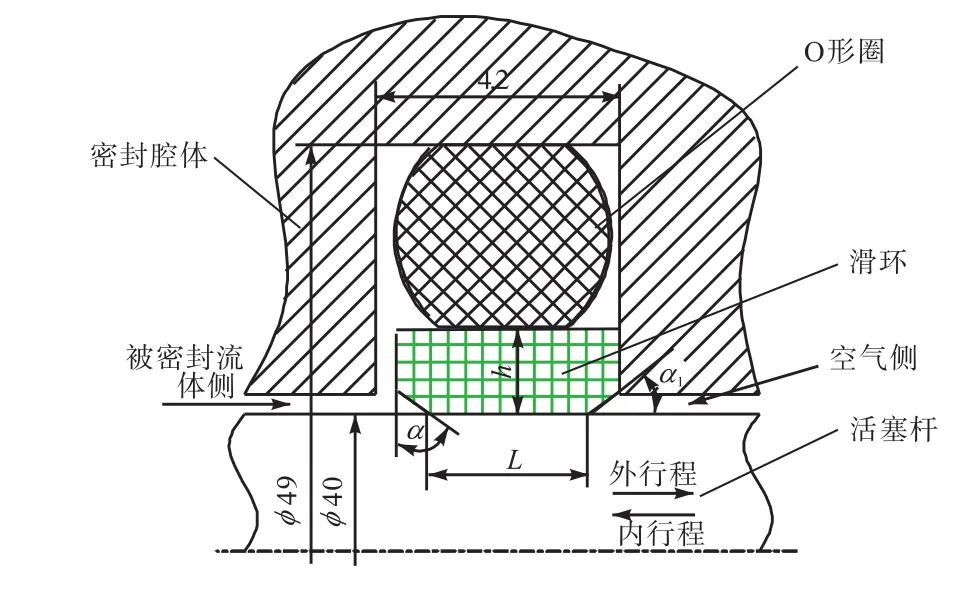
图1 方形同轴组合密封几何模型Fig.1 Geometric model of the rectangular coaxially combined seal
1.1方形同轴组合密封有限元模型的建立
利用ANSYS进行网格划分时,将活塞杆和腔体简化为刚性件,采用二维实体单元 PLANE42.橡胶O形圈使用 Mooney-Rivlin应变能函数描述,其中C10=1.87,MPa,C01=0.47,MPa.滑环和橡胶 O形圈采用二维实体单元 PLANE182.用面面接触单元CONTA172和TARGE169模拟活塞杆与滑环、腔体与滑环、腔体与橡胶 O形圈、滑环与橡胶 O形圈间的接触[5],具体参数见表1.
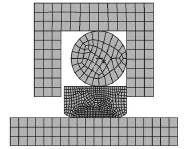
图2 方形同轴组合密封有限元模型Fig.2 Finite element model of the rectangular coaxially combined seal
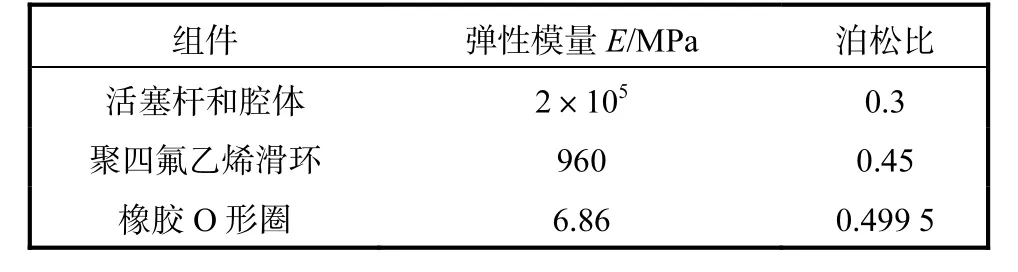
表1 方形同轴密封各组件的材料参数Tab.1 Material parameters of the seal’s components
1.2O形圈压缩率对主密封面密封性能的影响
O形圈的压缩率是方形同轴组合密封的一个重要参数,其大小对整体结构的密封性能具有较大的影响.一般 O形圈压缩率为 10%,~15%,[6],本文在4,MPa和 8,MPa两种油压下,对 O形圈取 10%,~20%,不同压缩率进行模拟仿真.图3所示为O形圈取不同压缩率时主密封面的最大接触压力曲线.
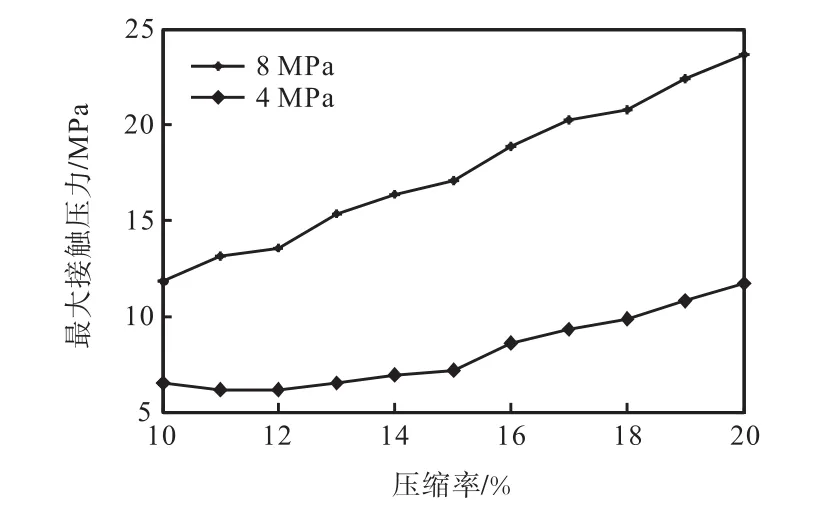
图3 最大接触压力与压缩率的关系曲线Fig.3 Curve of maximum contact pressure to compression ratio
由图3可以看见,在两种油压下均可达到密封要求,且油压越高时压缩率对最大接触压力的影响越大.在4,MPa油压下,当压缩率为10%,~15%,时,其对最大接触压力的影响相对平缓,当压缩率高于15%,时,随着压缩率的增加,最大接触压力明显增大;在8,MPa油压下,最大接触压力随着压缩率增加而增大,曲线斜率大于4,MPa油压下曲线斜率.长时间过大的接触压力会造成滑环与活塞杆接触面发生损伤,影响使用寿命.而且,压缩率过大还会使 O形圈产生较大变形(如图4所示),O形圈几乎充满整个腔体,O形圈长期处于较大变形状态下容易导致损坏.因此,方形同轴组合密封的O形圈压缩率的取值范围应控制在10%,~15%,.
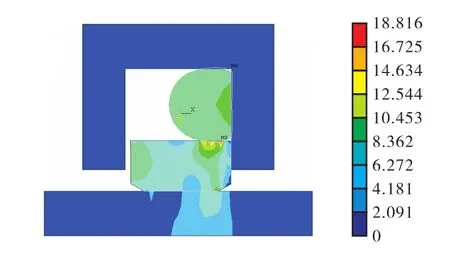
图4 压缩率为20%时应力云图(8,MPa)Fig.4 Von Mises stress at compression rate of 20%(8,MPa)
1.3滑环厚度对主密封面密封性能的影响
在具有代表性的高油压(8 MPa)下不同滑环厚度时的主密封面最大接触压力变化趋势如图 5所示.从图5可看出,主密封面的最大接触压力随滑环厚度增加单调递减,密封效果逐渐变差,当滑环厚度达到 4.6 mm时,出现不收敛的情况,且最大接触压力为2.302 MPa<8 MPa,此时已不能实现密封要求.
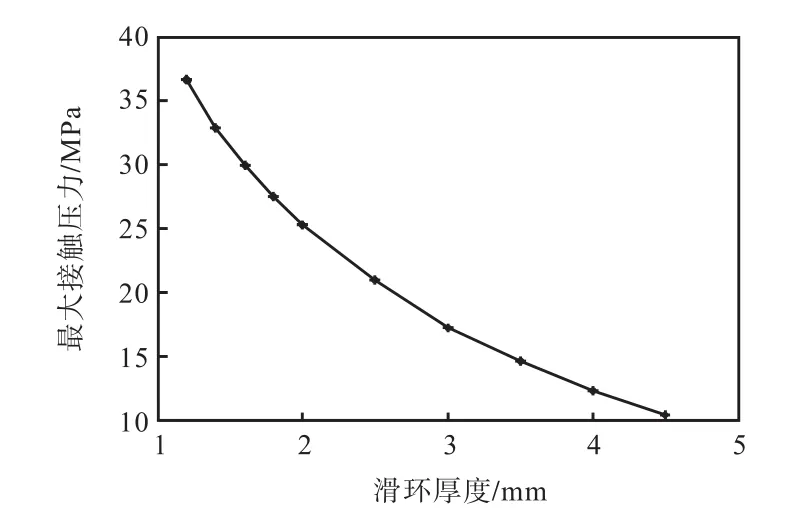
图5 不同滑环厚度时的最大接触压力值Fig.5 Maximum contact pressure with different thickness of the sliding ring
图 6为薄厚滑环在 8 MPa油压作用下的 Von Mises应力云图.可见,随着滑环厚度的增加 Von Mises应力的分布范围逐渐变小,最大应力值变化并不明显.滑环过厚,则刚性较大,滑环磨损后难以在压力作用下产生足够大的变形,从而易于泄漏[2];而滑环太薄,对冲击载荷较敏感,变形较大,容易因破坏导致泄漏.因此,应根据密封的不同工作介质压力合理设计滑环厚度,以保证其既有良好的密封性能又有较长的使用寿命.
阿勇告诉本刊记者,开庭前,林灿岗曾两度致电阿勇,要求其提前缴纳罚款,不然就判实刑。在阿勇提供的两段电话录音中,林灿岗多次提及罚金,“自留地也好,什么都好,也要罚款。这两三天拿六万块来交,不然要判实刑。”“今天是(8月)28号,30号之前没拿来交就要判实刑。”
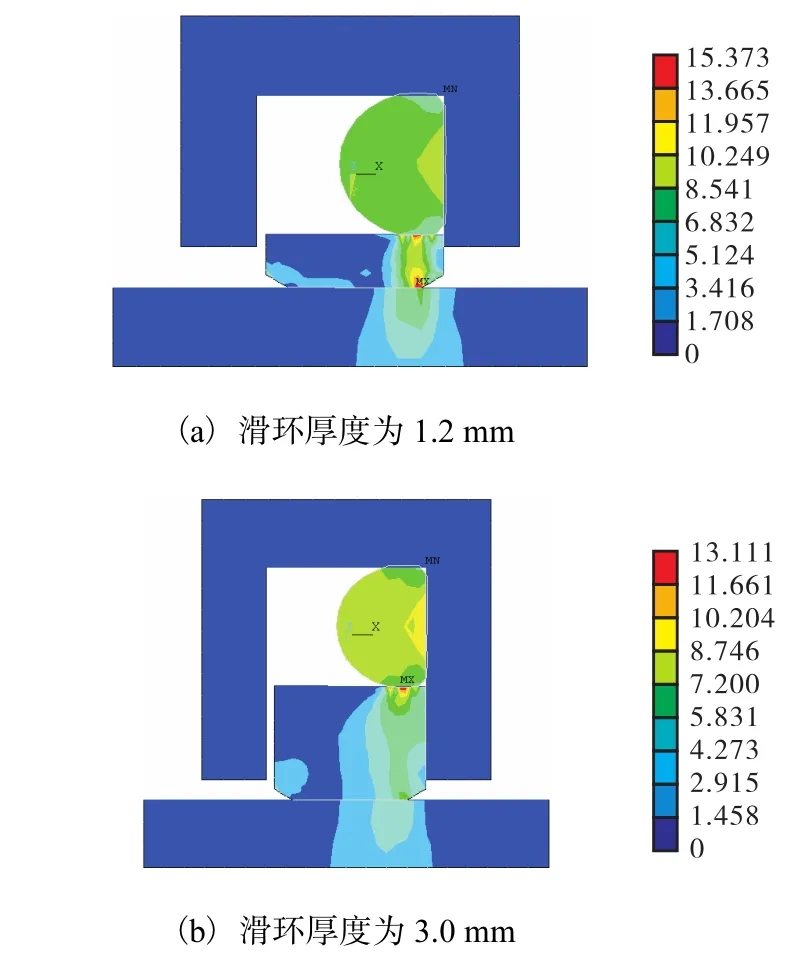
图6 薄厚两种滑环的Von Mises应力云图Fig.6 Von Mises stress of thin & thick sliding ring
1.4滑环两侧倒角对主密封面密封性能的影响
1.4.1滑环底倒角对密封性能的影响
在滑环与活塞杆接触宽度L=3.0 mm不变的前提下,使底倒角 α1从5°~65°变化,分析方形同轴组合密封的最大 Von Mises应力与密封面的最大接触压力,结果见图7.
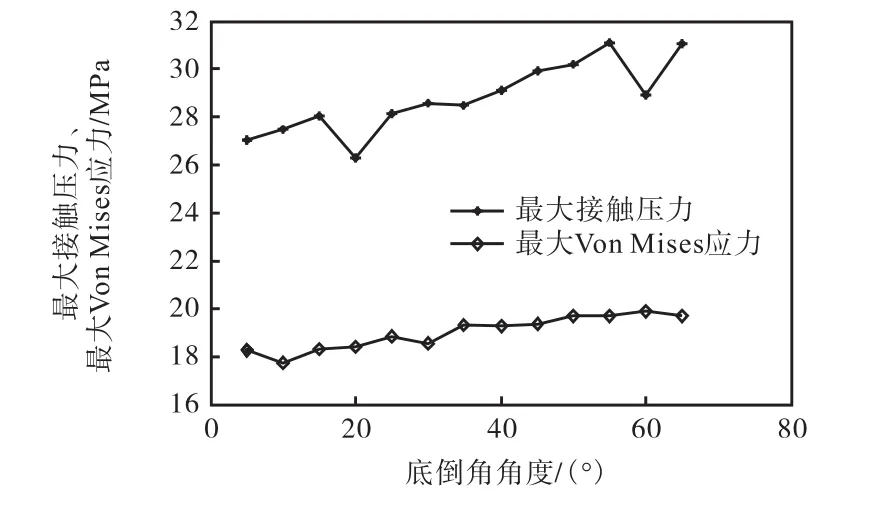
图7 最大接触压力、Von Mises应力与底倒角关系曲线Fig.7 Curve of maximum contact pressure,Von Mises stress and bottom chamfering
从图 7可以看出:当底倒角在 5°~65°内变化时,最大 Von Mises应力一直处于平缓增加的趋势,说明组合密封承受的综合应力相对较小且稳定,不容易发生疲劳损伤.而最大接触压力则随着底倒角增加近似呈线性增加,表明密封性能逐渐加强.
1.4.2滑环顶倒角对密封性能的影响
在滑环两侧底倒角 α1角度值与位置不变的情况下,对顶倒角α 在 5°~75°变化(即改变滑环与活塞杆的接触宽度 L)时进行了有限元仿真,结果如图 8所示.顶倒角取5°时,最大接触压力为6.777 MPa<8,MPa,不能实现密封;顶倒角在10°~70°变化时,最大接触压力值单调递增;当顶倒角取 75°时,滑环与活塞杆的接触宽度过小而出现了尖角,此时最大接触压力也骤增,达到 166.846 MPa.说明方形同轴组合密封的滑环与活塞杆的接触宽度不能过小.而最大Von Mises应力,除在75°时发生小幅跳跃外,一直处于平稳状态,且最大应力位置集中于滑环处,保证了橡胶O形圈的性能不受破坏.
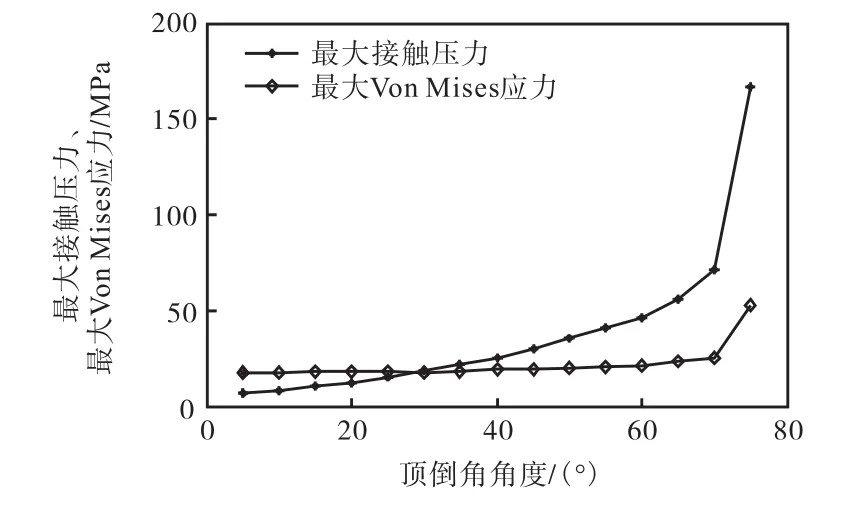
图8 最大接触压力、Von Mises应力与顶倒角关系曲线Fig.8 Curve of maximum contact pressure,Von Mises stress and top chamfering
2 运行参数对方形同轴组合密封的动态密封性能的影响
活塞杆的工作行程如图1所示,活塞杆向右运动时为外行程,活塞杆向左运动时为内行程.
2.1活塞杆运行速度对动态密封性能的影响
假设活塞杆内外行程的运动速度相同,当活塞杆的速度分别为 0.01、0.05、0.10、0.20、0.30、0.40、0.50 m/s时,方形同轴组合密封的最大接触压力和最大摩擦应力的仿真分析结果分别见图9和图10.
从图9可知,活塞杆外行程最大接触压力值明显高于内行程,说明该组合密封在不同往复运动速度下的密封性能较为稳定,且外行程的密封性能明显优于内行程,该分析结果与文献[7]结果一致.
从图 10可以看出,外行程的最大摩擦应力始终大于内行程;内外行程时的数值波动较小.说明往复运动速度对组合密封件的摩擦力影响较小.

图9 最大接触压力与活塞杆运行速度关系曲线Fig.9 Curve of maximum contact pressure and speed of piston rod
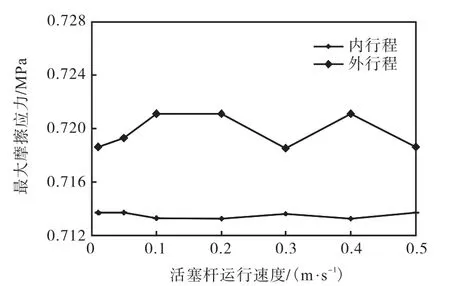
图10 最大摩擦应力与活塞杆运行速度关系曲线Fig.10 Curve of maximum friction stress and speed of piston rod
2.2滑环摩擦因数对动态密封性能的影响
滑环材料为聚四氟乙烯,无润滑摩擦因数达0.04,此处摩擦因数分别取 0.01、0.02、0.03、0.04,对主密封面的最大接触压力进行分析,结果如图 11所示.可见滑环的摩擦因数对主密封面最大接触压力影响不大,而且动态下密封往往处于动压或混合润滑状态,不会对最大摩擦应力产生较大影响,因此,可忽略摩擦因数对最大摩擦应力的影响.
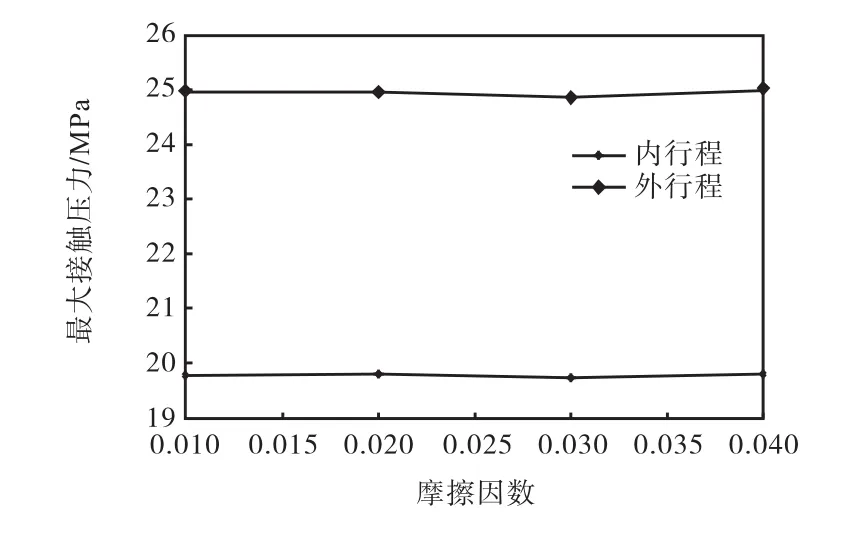
图11 最大接触压力与滑环摩擦因数关系曲线Fig.11 Curve of maximum contact pressure and sliding ring friction coefficient
3 基于响应曲面法的方形同轴组合密封结构参数优化
应用响应曲面法[8],以密封结构最大接触压力和最大摩擦应力具有望目特性为优化目标,对该组合密封的滑环厚度、滑环顶倒角角度、橡胶O形圈的压缩率三因子进行优化设计.从图 12和图 13中可以看到,等值线图的形状接近椭圆或直线,说明两因子之间交互效应显著.需要说明的是,在响应变量为最大接触压力时的方差分析中,厚度与压缩率的交互效应不显著(P=0.235>0.05);响应变量为最大摩擦应力时,厚度与后倒角的交互效应不显著(P=0.093>0.05),因此在计算中不需要考虑以上两个交互效应.
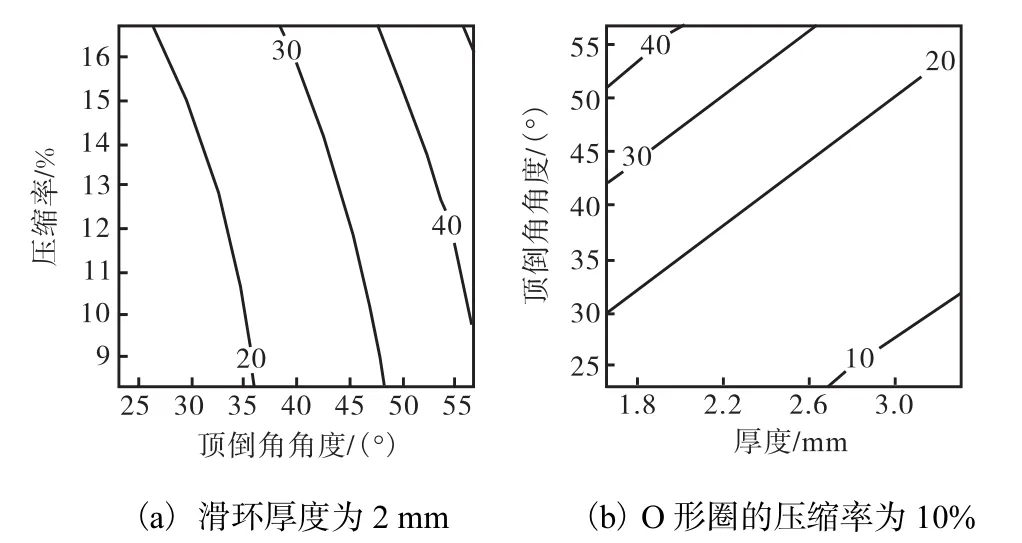
图12 响应变量最大接触压力的等值线图Fig.12 Contour line of response variables under maximum contact pressure
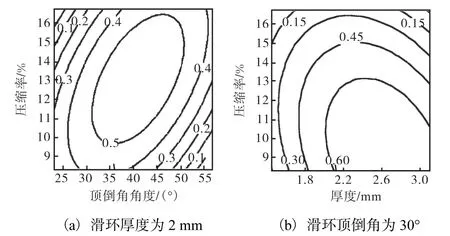
图13 响应变量最大摩擦应力的等值线图Fig.13 Contour line of response variables with maximum friction stress
滑环厚度、滑环顶倒角角度、橡胶O形圈的压缩率三因子的优化结果如图14所示,其中,y表示望目值,d表示合意性(即越接近设定目标,此值就越向 1靠拢).当方形同轴密封的滑环厚度为2.03,mm,顶倒角角度为33.26°,压缩率为16.70%,时(由于橡胶件不可能加工到软件计算的精度,所以保留两位小数),达到期望值,密封性能最优.
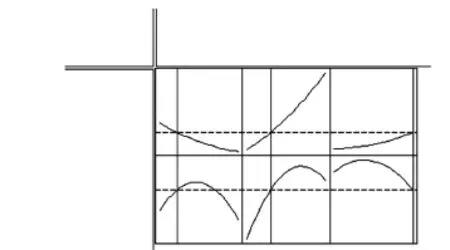
图14 响应变量优化图Fig.14 Optimization of the response variables
4 结 论
(1)方形同轴组合密封主密封面的最大静态接触压力随滑环厚度的增加而减小,随滑环顶倒角的增大而增大,随压缩率的增大缓慢增大.
(2)活塞杆往复运行速度及滑环的摩擦因数对方形同轴密封的动态密封性能影响较小.
(3)根据响应曲面分析结果,当滑环厚度为 2.03 mm、滑环顶倒角为 33.26°、压缩率为 16.70%,时,密封性能最优,可实现最大接触压力25 MPa,最大摩擦应力0.3 MPa的优化目标.
[1] 谭晶,杨卫民,丁玉梅,等. 滑环式组合密封件的研究(I):方形同轴密封件(格来圈)的分析[J]. 润滑与密封,2007,32(1):53-55.
[2] 谭晶,梁军,杨卫民,等. 滑环式组合密封件的研究(Ⅱ):阶梯形同轴密封件(斯特圈)的有限元分析[J].润滑与密封,2007,32(7):16-19,74.
[3] 陈国栋. 常温低温组合密封结构的有限元分析与优化设计[D]. 哈尔滨:哈尔滨工业大学,2008:37-43.
[4] 郑辉,张付英. 液压往复密封泄漏量的有限元分析[J].机床与液压,2011,39(8):58-61.
[5] 王成刚,肖健,刘慧,等. 格莱圈密封性能非线性有限元分析[J]. 武汉工程大学学报,2014,36(2):42-48.
[6] 钟亮,赵俊利. 往复式密封中O形密封圈组合的有限元分析[J]. 橡胶工业,2014,61(4):231-235.
[7] 李腾. Y型密封圈儿的密封性能计算分析[D]. 天津:天津科技大学,2014:47-60.
[8] Makadia A J,Nanavati J I. Optimization of machining parameters for turning operations based on response surface methodology[J]. Measurement,2013,46(4):1521-1529.
责任编辑:常涛
Optimization of the Structure and Operating Parameters of Rectangular Coaxially Combined Seal
ZHANG Fuying,SUN Yujia,JIANG Xiangmin
(Tianjin Key Laboratory of Integrated Design and On-line Monitoring for the Light Industry and Food Engineering Machinery and Equipment,College of Mechanical Engineering,Tianjin University of Science & Technology,Tianjin 300222,China)
ANSYS was used to analyze the impact of the rectangular coaxially combined seal’s structure and operating parameters on the static and dynamic sealing performance.The results showed that the maximum static contact pressure of the primary sealing surface decreased significantly with the increase of the sliding ring’s thickness,but increased with the growing of both sides of the sliding ring’s chamfering and O-ring compression rate.The influence of the reciprocating motion speed of the piston rod and the friction coefficient of the sliding ring on the maximum dynamic contact stress of the primary sealing surfaces and the friction between the sealing surfaces was not obvious.In order to realize the optimization target of getting maximum contact pressure and minimum friction of the sealing surface,the structural parameters of the combined seal were optimized by applying the response surface method,and the best structural parameters were obtained.The rectangular coaxially combined sealing property was the best when the sliding ring’s thickness was 2.03,mm,the top chamfering angle 33.26°,and the O-ring compression rate 16.70%,.
rectangular coaxial combined seal;finite element analysis;parameter optimization;response surface methodology
TB42
A
1672-6510(2016)04-0060-05
10.13364/j.issn.1672-6510.20150169
2015-10-19;
2016-01-17
国家自然科学基金资助项目(51075300)
张付英(1965—),女,河北人,教授,zhfuying@tust.edu.cn.

