非线性互补问题的光滑算法

朱红焰，岳靖，巩成艳

（安徽理工大学 理学院，淮南 232001）

非线性互补问题的光滑算法

朱红焰，岳靖，巩成艳

（安徽理工大学 理学院，淮南 232001）

基于非线性互补问题（NCP（F））的等价变形，利用Fischer-Burmeister函数的光滑逼近函数将非线性互补问题转化为优化问题。提出了一种求解非线性互补问题的光滑逼近算法，通过构造非线性互补问题的一个新的光滑逼近函数，将非线性互补问题等价地转化为求解光滑方程组问题。在一定条件下证明了该算法的全局收敛性。数值实验结果说明了算法的有效性。

非线性互补问题；光滑逼近算法；全局收敛性

考虑以下非线性互补问题NCP(F):求向量x∈Rn使得

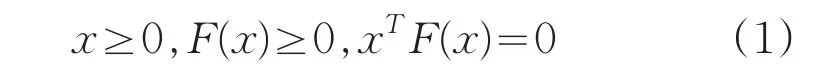
其中F∶Rn→Rn连续可微的P0-函数。

由于其在理论和实际应用上的重要性，近年来，非线性互补问题已经受到了许多研究者的关注。

首先，给出Fischer-Burmeister函数:

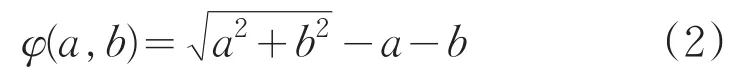
求非线性互补问题（1）等价转化为求解以下非线性方程组:

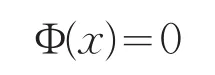
且Φ∶Rn→Rn，它的第i个分量由下面的表达式给出:

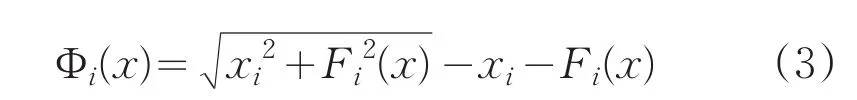
Fischer-burmeister函数有很多好的性质，在求解NCP（1）时，一般都以Fischer-Burmeister函数作为 NCP函数，但是Fischer-burmeister函数在(a,b)=(0,0)点是不可微的，给算法的收敛性分析带来困难，于是光滑算法应运而生。

本文构造一个新的光滑NCP函数如下:

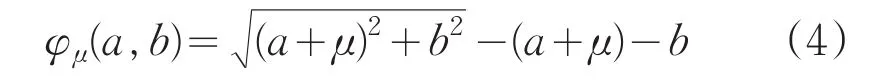
对于任意的μ1＞μ≥0，有:

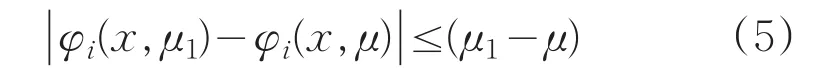
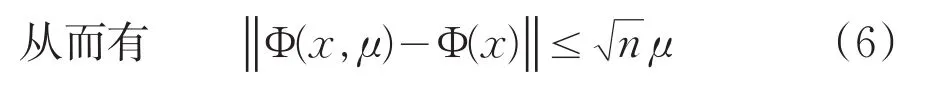
引理1:若Φ(x,μ)，Φ(x)是如上所定义的，则Φμ是Φ的一致光滑逼近函数。通过简单计算得

利用光滑逼近函数，问题可以转化为下面带约束的非线性方程组

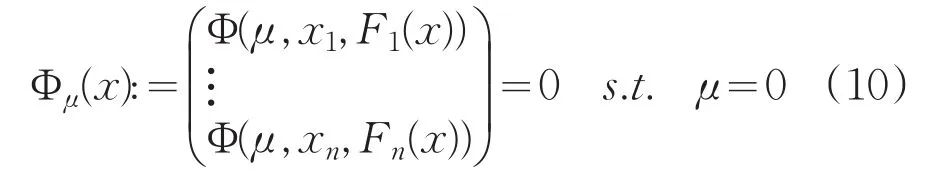
显然，当μ＞0时，Φμ(x)是光滑的，且其Jacobi矩阵∇Φμ(x)T为:

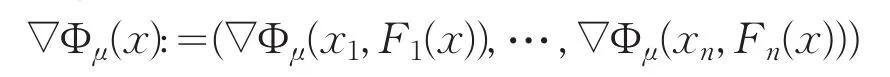
其中，Jacobi矩阵的第i个分量为

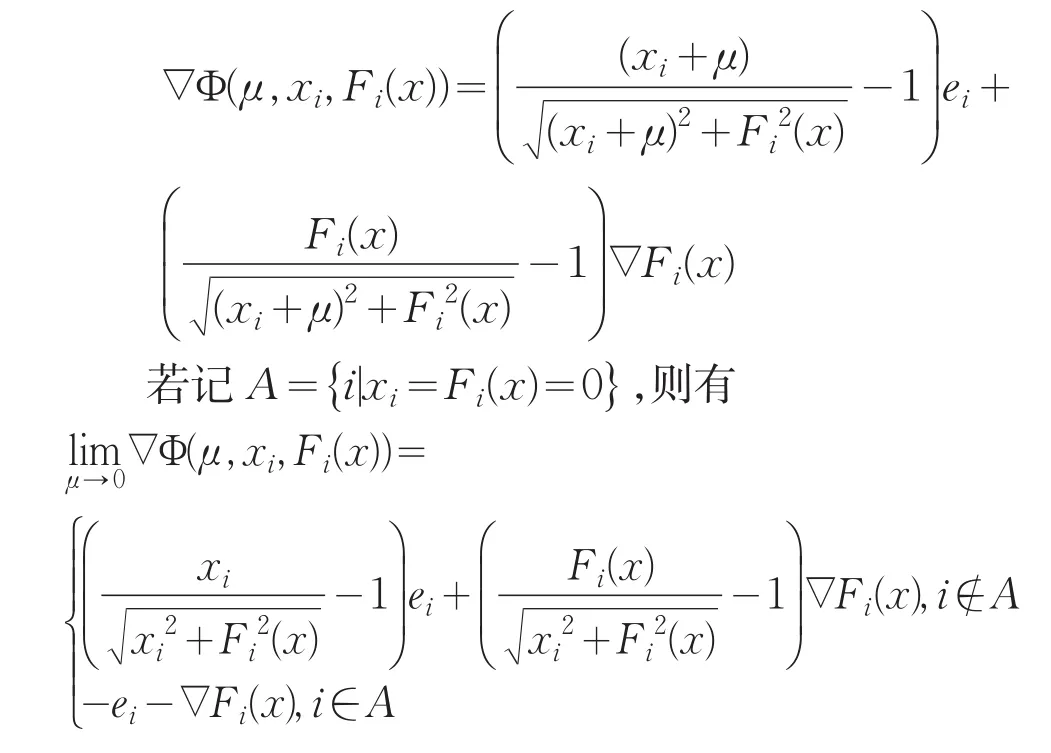
1 算法

算法1:

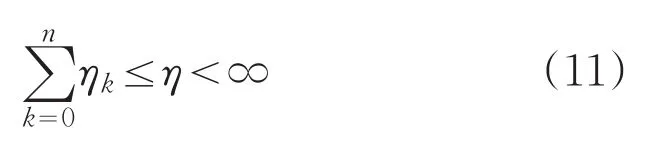
其中，η＞0，选取初始点 x0∈Rn和正常数置k∶=0，

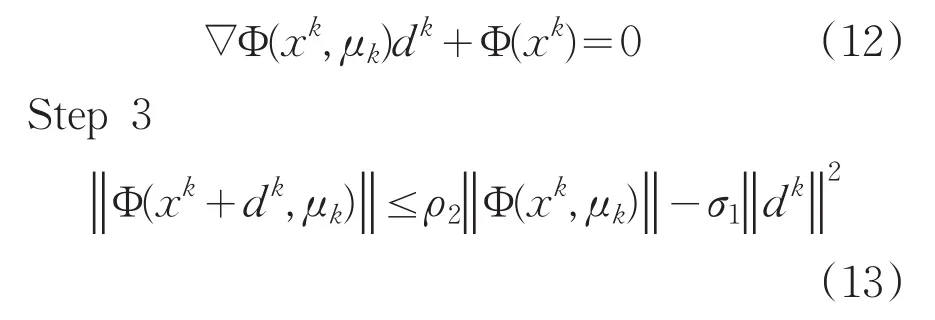
若式（13）成立，置λk∶=1，转step5；

Step4 若m是满足下属不等式的最小非负整数

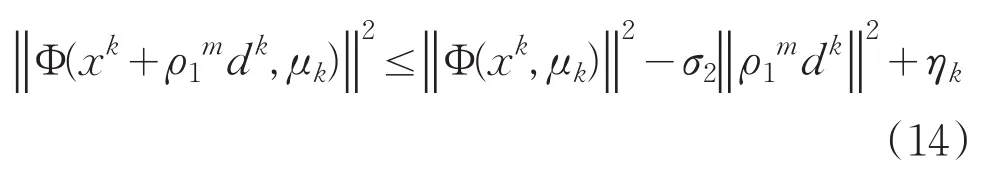
置λk∶=ρ1m；

Step5 置xk+1∶=xk+λkdk；

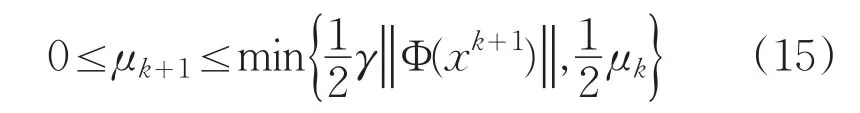
否则，置μk+1∶=μk；

Step7 置k∶=k+1，转Step2

注1:由于 ηk＞0，总可以选取充分小的λ=ρ1i＞0，使得不等式（14）成立，从而算法是可行的。

注2:若是{xk}是由于算法产生的无穷数列，则对于任意的k满足Φ(xk,μk)≠0，且正数序列{μk}是非增的，并且满足式（16）:

则由于式（6）和式（16）可以得到证明如下:

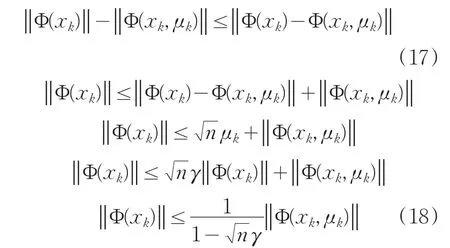
从而可以得到式（19）:

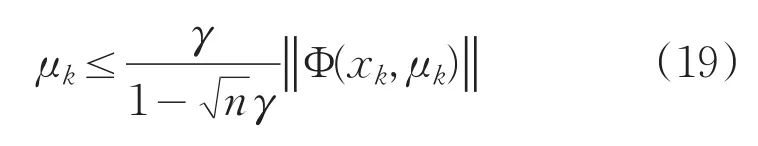
2 全局收敛性

假设

（b）对于任意的μ＞0，Φ'(x,μ)非奇异，且x∈Ω。

引理2:设序列{xk}是由算法产生的，那么对于任意的k，有{xk}⊂Ω,

证明:对于算法1中步3中的式（13），结论显然成立，对于步4中的式（14），有:

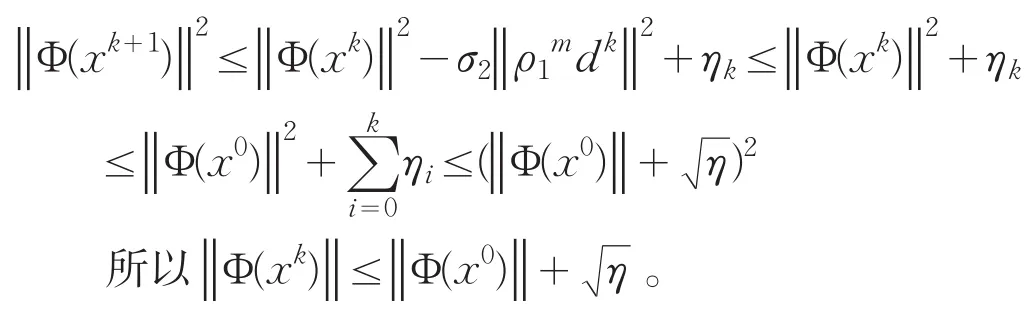
引理3:设序列{xk}由算法产生，定义指标集其中:

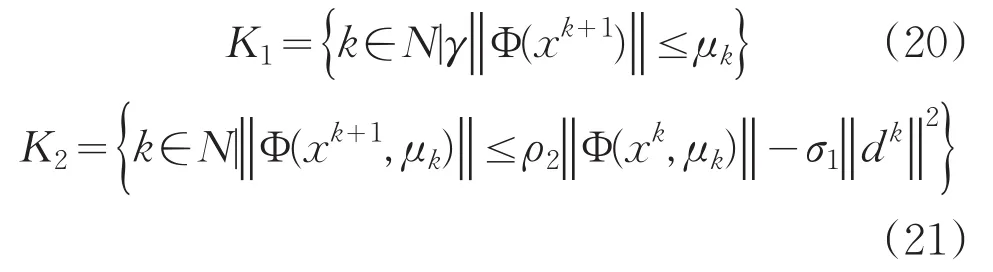
若指标集K为无限集，那么:

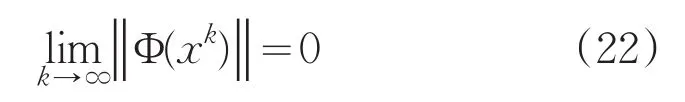
且序列{xk}的任意聚点是问题（1）的解。

证:由题中K为无限集，又因K={0}⋃K1⋃K2，故只需要考虑以下两种情况:

情形1:K2是无限集.此即意味着（21）式无限次成立，而ρ2∈(0,1)，故由引理即可得（22）成立。

情形2:K2是有限集，但K1是无限集，不失一般性，设对任意的非负整数k，记即ki是 K中不大于k的最大指标，则显然有μk=μki。

由（17），对i≥0，有:

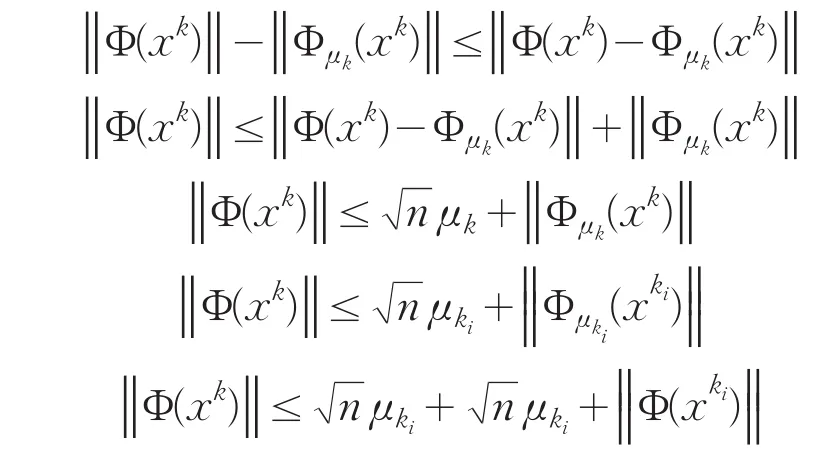
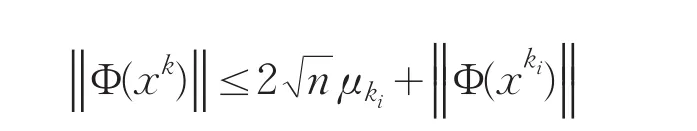
由算法的step 6可知

以及

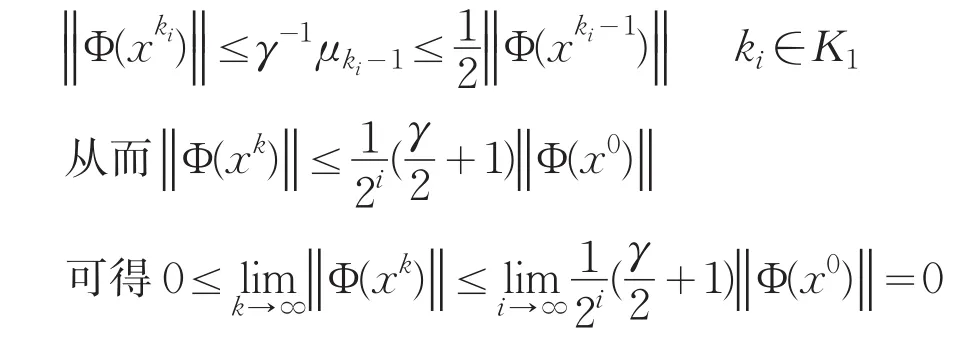
综上表明序列{xk}的每个聚点都是Φ(x)的一个零点，即问题（1）的一个解。

定理1:设假设成立，序列{xk}由算法产生，那么指标集K必是无限集，且

证明:用反证法，假设K是有限集，K采用情形2的假设方式，则μk=μki=μ，且步长λk由（14）确定，即

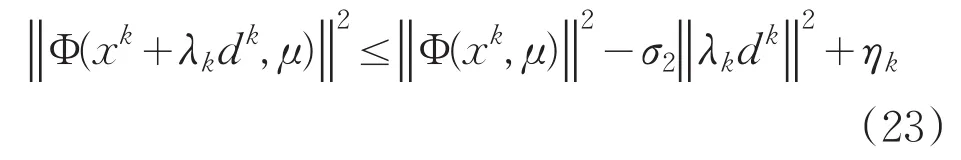
由假设（b），存在常数 M1＞0，使得

因此，对于充分大的K，有

（a）当 λ＞0时，有 d=0则由（12）式即得Φ(x)=0，矛盾。

对上式两端同时除以λk'，且令k(∈K)→∞，得

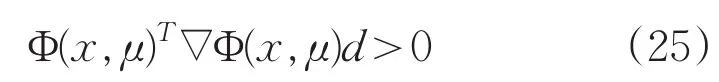
由于-∇Φ(xk,μ)dk=Φ(xk)，令k(∈K)→∞，得

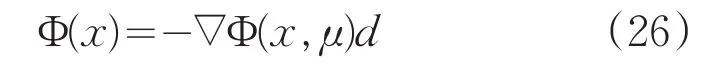
又由（26）式得

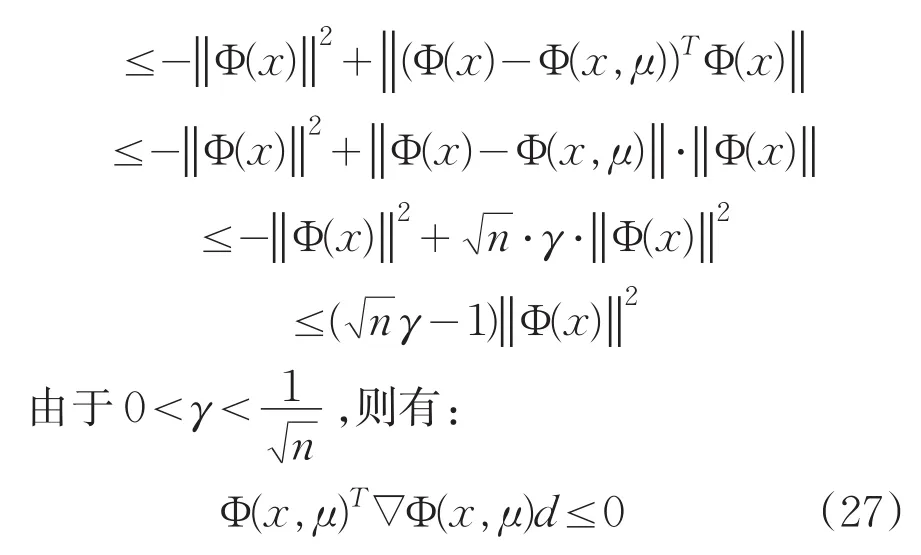
因此式（25）与式（27）矛盾，从而K为无限集.

3 数值试验

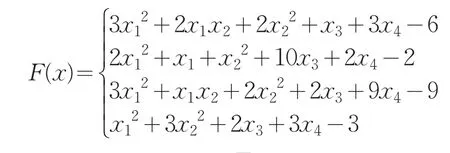
表1 数值结果

4 结论

论文将NCP问题转化为光滑方程组来求解，构造了相应的光滑逼近算法，证明了在一定条件下该算法的全局收敛性，同时给出数值试验来验证算法的时效性，下一步工作的重点是证明算法的局部二次收敛和超线性收敛，以及算法产生的迭代序列至少存在一个聚点。

［1］ 许小芳，马昌风.基于一个新的NCP函数的光滑牛顿法求解非线性互补问题［J］.数学杂志，2011，31（4）: 750-755.

［2］ 范斌，马昌凤.求解非线性互补问题的一个雅可比光滑化方法［J］.福建师范大学学报，2012，28（3）:27-31.

［3］ 张修梅，蒋利华.非线性互补问题的光滑逼近法［J］.安徽大学学报，2012，36（2）:24-28.

［4］ 陈争，马昌凤.求解非线性互补问题的一个新的Jacobin光滑化方法［J］.计算数学，2010，32（4）:362-372.

［5］ 柴婧，马昌凤.求解广义非线性互补问题的光滑拟牛顿算法［J］.高校应用数学学报，2011，26（4）:453-466.

［6］ 于一超，田志远，刘相静，等.非线性互补问题的一个数值解法［J］.青岛大学学报，2014，27（3）:14-18.

［7］ 韩继业，修乃华，戚厚锋.非线性互补理论与算法［M］.上海:上海技术科学出版社，2003:248-296.

［8］ 马昌凤.最优化方法及其Matlab程序设计［M］.北京:科学出版社，2010:53-68.

A Smoothing Algorithm for Nonlinear Complementarity Problems

ZHU Hongyan，YUE Jing，GONG Chengyan
（School of Science，Anhui University of Science and Technology，Huainan 232001）

Based on the equivalent deformation of nonlinear complementarity problems（NCP（F））and the use of smooth approximating functions of Fischer-Burmeister function，the problem is transformed into optimization problem.A smoothing approximation algorithm is proposed for solving the nonlinear complementarity problem.By introducing a new smoothing NCP-function，the problem is approximated by a family of parameterized smooth equations.The proposed algorithm has been proved to be globally convergent under certain conditions.Numerical experiment results demonstrate the effectiveness of the algorithm.

nonlinear complementarity problem；smoothing approximation algorithm；gobal convergence；

O224

A

1672-9870（2016）05-0127-04

2016-05-30

朱红焰（1992-），女，硕士研究生，E-mail:1213096843@qq.com