一种改进的多尺度可能性聚类算法

胡雅婷，曲福恒

（1.吉林农业大学 信息技术学院，长春 130118；2.长春理工大学 计算机科学与技术学院 长春 130022）

一种改进的多尺度可能性聚类算法

胡雅婷1，曲福恒2

（1.吉林农业大学 信息技术学院，长春 130118；2.长春理工大学 计算机科学与技术学院 长春 130022）

针对多尺度可能性聚类算法（MPCM）计算复杂度较高的问题，提出一种改进的多尺度可能性聚类算法（IMPCM）。算法利用k-均值聚类的收敛点来作为MPCM的初始点，在继承了MPCM优点的同时，解决了原始MPCM中无效初始点过多以及初始点位置不理想造成的迭代次数过高的问题。对比实验结果表明，算法具有良好的聚类效果与更高的计算效率。

k-均值聚类；可能性聚类；均值漂移

1996年，Krishnapuram与Keller提出了可能性模糊c-均值聚类（PCM）算法［1］，PCM放松了模糊c-均值聚类（FCM）算法［2］的概率型约束条件，能够解决FCM算法受噪声影响的问题。但PCM算法模型本身固有的模式也引发了新的问题，即算法对初始化参数敏感，且容易产生重合的聚类［3］。为此，有多种改进的可能性聚类算法被提出［4-7］。Yang与Wu同时考虑到FCM的目标函数和两个聚类有效性指标［4］，使其提出的算法适用于无监督聚类。Pal等人综合考察模糊聚类和可能性聚类算法，先后提出两种混合聚类模型［8］。为了解决PCM对MPCM算法的时间复杂度主要取决于均值漂移聚类的初始点个数和迭代次数，算法的初始初始化敏感及发现数据集的不同尺度聚类结构问题，Hu等于2010年提出MPCM算法［9］。点是通过网格剖分方法获得的，这种方法首先对数据空间的进行网格剖分，再在每个剖分的网格内选择一些（个）特征点作为MSC的初始迭代点。这种方法虽然可以将MSC的计算量降低到O(nl)（n是数据的个数，l是网格剖分后特征点的个数），但在实验中发现，由于在每个网格中都必须选择一些（个）特征点作为MSC的初始迭代点，而其中的很多特征点与聚类中心的相距较远，需要通过均值漂移聚类一步步迭代才能收敛到聚类中心。这样，均值漂移聚类的初始点个数远高于实际的聚类中心数目，而这些初始点收敛到真实聚类中心进行迭代的次数也是非常高的。为了解决MPCM算法的计算复杂度问题，本文采用k-均值聚类算法代替网格剖分技术进行初始点的选取。k-均值聚类算法是目前应用最为广泛的硬聚类算法，具有计算简单，适合处理大数据集等优点［10］。

本文采用k-均值聚类算法获取均值漂移聚类的初始点，提出一种改进的多尺度可能性聚类算法。算法在保留MPCM算法优点的同时，有效解决了MPCM时间复杂度过高的问题。

1 聚类算法

给定数据集合X={x1,x2,…,xn}⊂RS，n为样本个数，将样本集X划分为c(2≤c≤n)类。设数据集合X的c-划分表示为矩阵U=[uij]，对应X的可能性c-划分、模糊c-划分和硬c-划分空间分别为:

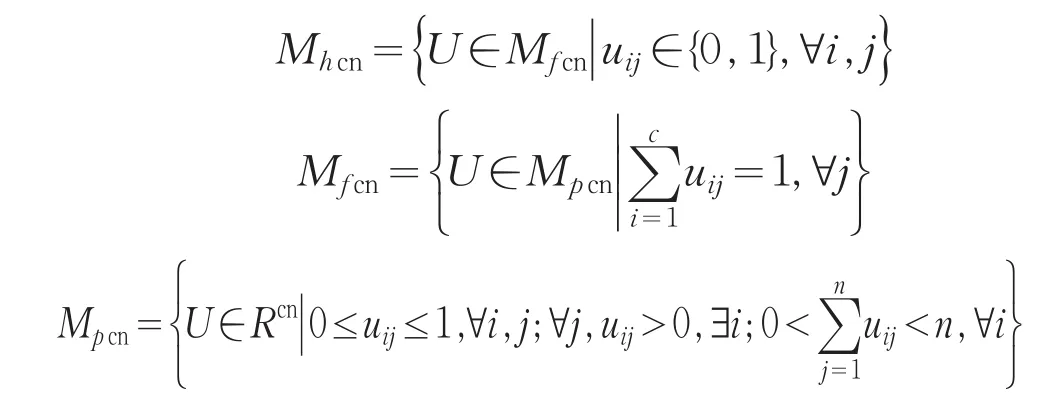
对于硬划分或模糊划分矩阵U，uij表示xj关于X的第i个聚类的隶属度，二者的区别是硬划分的隶属度只取0与1两个值，模糊划分取值在[0,1]区间上。而对于可能性划分矩阵U，uij表示xj属于第i类的可能性。

1.1 k-均值聚类

k-均值聚类算法是一种基于划分的聚类算法，其计算简单、实现效率高的特点使其适合处理大数据集，是目前应用最为广泛的聚类算法之一。k-均值聚类算法通过最小化误差平方和函数获得聚类划分，具体步骤为:

步骤1:随机初始化聚类中心:

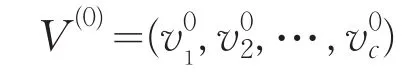
步骤2:将每个样本xj分配到与之距离最近的聚类中心；

步骤3:重新计算各类的聚类中心:

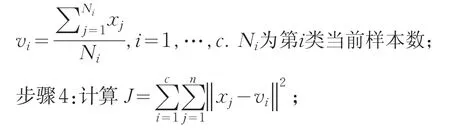
步骤5:如果J值收敛，则return(v1,v2,…,vc)，算法终止；否则，转步骤2。

1.2 可能性聚类算法

可能性聚类算法应用可能性理论研究聚类问题，放松了模糊聚类算法中对隶属度的概率型约束。PCM聚类模型可以通过最小化目标函数Jpcm得到:

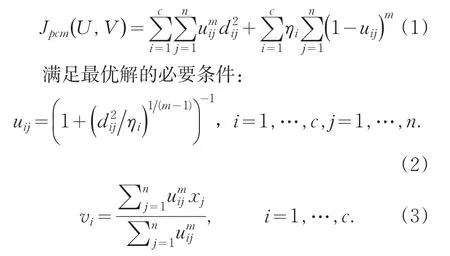
将式（2）、（3）迭代直至收敛直至得到满足目标函数Jpcm的最优解。其中m为模糊系数，U=[uij]c×n表示可能性划分矩阵，uij表示第 j个样本点属于第i类的可能性。

2 改进的可能性聚类算法

均值漂移算法（MS）最初是用核方法对非参密度函数梯度估计得到的，其良好的特性在图像分割、目标跟踪、数据融合［11-13］等计算机视觉领域得到了广泛地应用。给定s维特征空间中的数据集合由核函数K(·)与带宽参数h确定的概率密度估计函数为:

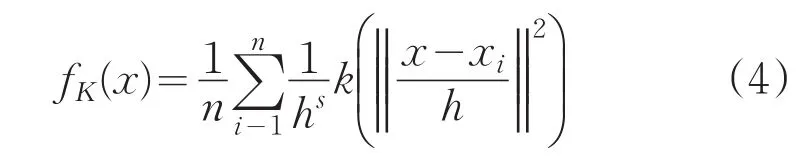
其中k(·)为核函数K(·)的轮廓函数，满足K(x)=αk(‖x‖2)，α为归一化常数。对 fK(x)求梯度并令其为0，得到均值漂移向量:

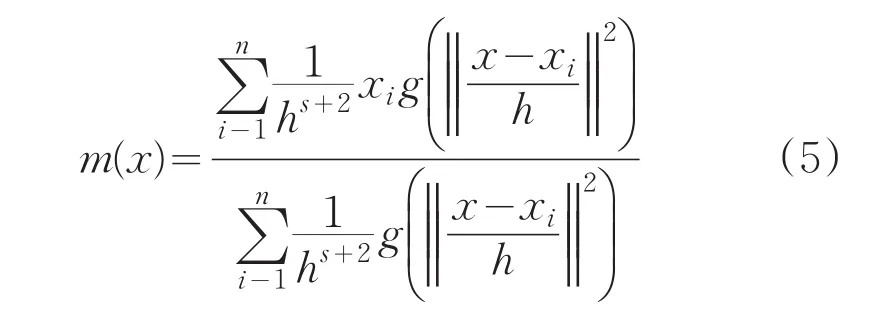
其中m(x)是沿着 fK(x)最大速度上升方向，因而达到概率密度函数局部极值的均值漂移迭代序列x(k-1)=x(k)+m(x(k))，是沿着函数值增加方向的。

为了降低均值漂移聚类的计算复杂度，采用k-均值聚类算法进行初始化。改进的多尺度可能性聚类算法（IMPCM）的具体步骤如下:

采用k-均值聚类算法对数据集合进行聚类划分，将得到的聚类中心(v1,v2,…,vc)作为均值漂移聚类的初始点；

表1 MPCM与IMPCM各部分对比

表2 data_A上不同算法的正确率（聚类个数c=12）

设定均值漂移聚类的核函数K(·)，hz，运行次数z=0；

更新z=z+1；

分别以vk，k=1,2,…,c作为初始迭代点，迭代式（4）、（5）直至收敛，记为

IMPCM算法采用均值漂移聚类对PCM进行初始化，保留了MPCM算法对初始化鲁棒及能够发现数据集的不同尺度聚类结构的优点。同时，采用k-均值聚类算法对均值漂移聚类进行初始化，将均值漂移聚类的初始点个数从O(nl)降为c（k-均值聚类的聚类中心数目）个，有效降低了均值漂移聚类的初始点个数和迭代次数，改善了算法的计算复杂度。

3 实验分析

为了测试提出算法的性能，我们在具有多尺度聚类结构的数据集data_A上对IMPCM与MPCM及PCM的几种改进算法进行对比实验。

3.1 与MPCM对比实验

如图1所示，data_A数据集合是一个具有12个聚类的二维数据集合，其中每类包含25个数据点。图1（a）与图1（b）中的红色加号分布为IMPCM与MPCM两种算法获得的均值漂移聚类的初始化结果。从图中可以看出，利用k均值初始化的点都位于每个聚类的中心或中心附近，这些点不仅数目上比MPCM的要少，而且由于距离真实中心较近，后期的迭代次数也会远远小于MPCM，从而节省计算量。而在MPCM算法中，采用网格剖分方法确定的特征点作为均值漂移的初始点，这些特征点均匀分布在数据所在的空间中，即使在不存在数据点的空间内，也会按照均匀分布的原则产生出这部分空间的特征点，比如中间没有数据的部分，从而在之后的均值漂移聚类中产生无效的冗余计算量。

图1 不同方法的初始化结果

表1为MPCM与IMPCM算法各部分运行时间的对比。从表中可以看出，在算法的各个步骤中，包括均值漂移聚类初始化，均值漂移聚类的时间及迭代次数，PCM算法的运行时间，IMPCM的时间都有明显的降低。因而，从总的运行时间来看，IMPCM仅为MPCM算法的三分之一。从实验的对比结果可以看出，k-均值算法解决了网格剖分所带来多余初始点问题，有效地降低了计算复杂度。

3.2 与PCM的几种改进算法的对比实验

本实验中，选取PCM及其几种改进算法（包括IPCM、PFCM、MPCM）、均值漂移聚类（MSC）与提出的IMPCM算法进行对比实验。表2给出了聚类的准确率和算法的运行时间两方面结果。首先，从聚类准确度来看，MPCM、MSC及IMPCM都能够正确地揭示出数据集当聚类个数c=12时的聚类结构。而其它几种可能性聚类算法都产生一些误差，其最高正确率也不足90%，最差的IPCM-u（f）仅为32.07%。其次，从算法的运行时间上看，MPCM与MSC的运行时间较长，都超过了1秒，其他几种聚类算法都低于1秒。运行时间最短的为PFCM算法，仅为0.0833秒，但这种算法的聚类准确率较低，仅为88.07%。而剩余的四种算法的运算时间相近，在0.3～0.4秒之间，但只有IMPCM算法的聚类准确度最高。因此，综合聚类准确度和运算时间两个方面，本文提出的IMPCM算法的性能最优。

4 结论

本文针对MPCM中网格剖分选取的初始点带来的计算复杂度问题，采用k-均值聚类进行初始化，有效地降低MPCM算法的计算复杂度。实验表明，与MPCM以及均值漂移聚类相比，IMPCM算法在不降低聚类效果的前提下具有更高的计算效率。与PCM及其改进算法相比，在时间复杂度略有增加的前提下具有更好的聚类效果。在今后的研究中，如何更大幅度的降低算法的时间复杂度使之更适用于大数据集聚类，是我们需要进一步深入研究的课题。

［1］ Krishnapuram R，KellerJM.A possibilisticapproach to clustering［J］.IEEE Transactions on Fuzzy Systems，1993，1（2）:98-110.

［2］ Bezdek JC.Pattern recognition with fuzzy objective function algorithms［M］.New York:Plenum Press，1981.

［3］ Barni M，Cappellini V，Mecocci A.Comments on“A possibilisticapproachtoclustering”［J］.IEEE Transactions on Fuzzy Systems，1996，4（3）:393-396.

［4］ Yang MS，Wu KL.Unsupervised possibilistic clustering［J］.Pattern Recognition，2006，39（1）:5-21.

［5］ Hu Y，Qu F，Yang Y，et al.An Improved Possibilistic Clustering Based on Differential Algorithm［C］//2010 2nd International Workshop on Intelligent Systems and Applications，2010:1-4.

［6］ 胡雅婷，左春柽，曲福恒，等.基于改进可能性聚类算法的轴承故障诊断［J］.长春理工大学学报:自然科学版，2011，34（3）:58-61.

［7］ 胡雅婷.可能性聚类方法研究及应用［D］.长春:吉林大学，2012.

［8］ Pal NR，Pal K，Keller JM，et al.A possibilistic fuzzy c-means clustering algorithm［J］.IEEE Transactions on Fuzzy Systems，2005，13（4）:517-530.

［9］ 胡雅婷，左春柽，曲福恒，等.多尺度可能性聚类算法［J］.长春理工大学学报:自然科学版，2010，33（4）: 124-127.

［10］ Forgy E W.Cluster analysis of multivariate data: efficiency versus interpretability of classifications［J］.Biometrics，1965，21:768-769.

［11］ Comaniciu D，Ramesh V，Meer P.Kernel-based object tracking［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2003，25（5）: 564-575.

［12］ Debeir O，Van Ham P，Kiss R，et al.Tracking of migrating cells under phase-contrast video microscopy with combined mean-shift processes［J］. Medical Imaging，IEEE Transactions on，2005，24（6）:697-711.

［13］ Chen H，Meer P.Robust fusion of uncertain information［J］.Systems，Man，and Cybernetics，Part B: Cybernetics，IEEE Transactions on，2005，35（3）: 578-586.

An Improved Multi-scale Possibilistic Clustering Algorithm

HU Yating1，QU Fuheng2
（1.School of Information and Technology，Jilin Agriculture University，Changchun 130118；2.School of Computer Science and Technology，Changchun University of Science and Technology，Changchun 130022）

To overcome the problems of having a high computation of multi-scale possibilistic clustering algorithm（MPCM），an improved algorithm is proposed in this paper.IMPCM uses the convergent points of k-means to initialize MPCM.IMPCM inherits the merits of the MPCM.In the meanwhile，IMPCM solves the problem of MPCM that the initialization points are superfluous and the position is not ideal which make MPCM has too many iteration times. The contrast experiments show that IMPCM has a good clustering results and high computational efficiency.

K-means clustering；possibilistic clustering；mean shift

TP391.4

A

1672-9870（2016）05-0115-04

2016-06-15

吉林省教育厅“十二五”科学技术研究项目（2015201），吉林省教育厅“十三五”科研规划重点课题（2016186），吉林省教育科学规划课题（GH150221）

胡雅婷（1979-），女，博士，讲师，E-mail:huyating79@163.com

曲福恒（1979-），男，博士，副教授，E-mail:qufuheng@163.com