基于Davies理论的粗糙面光散射特性研究

王耀东，陈桂波，张烨，韩颖，谭勇，蔡红星

（长春理工大学 理学院，长春 130022）

基于Davies理论的粗糙面光散射特性研究

王耀东，陈桂波，张烨，韩颖，谭勇，蔡红星

（长春理工大学 理学院，长春 130022）

基于Davies理论，利用BRDF描述散射特性，系统考察了BRDF随角度、波长及粗糙度等参数的变化规律。数值结果表明，粗糙面的BRDF在形态上有一定的类镜面散射特性同时在镜面方向出现“高光”区域；入射天顶角越大则散射越趋于镜面反射；波长越小，粗糙面的相对粗糙程度越大，则Davies理论模型非镜面反射部分比重也越大。结果表明研究可为复杂实体散射分析与应用提供一定的理论依据和指导。

Davies理论；双向反射分布函数；粗糙面

研究粗糙面散射特性［1］，进而掌握其光散射规律是对复杂物体散射［2］规律研究的基础和前提［3］，而表面散射特性通常用双向反射分布函数（Bidirectional Reflectance Distribution Function，BRDF）来描述。

BRDF最早由Nicodemus于1970年提出［4］。各国学者在理论上、仪器设备研制的应用［5］上进行了大量的研究。理论模型方面先后有Davies于1954年假定表面高度起伏服从高斯分布并应用基尔霍夫近似提出Davies模型［6］，Torrance和Sparrow于1967年由基于微平面分布理论并假定粗糙面由V型凹槽构［7］成提出Torrance-Sparrow模型［8］，Maxwell和Beard于1973年提出包含表层和内层反射贡献的漆面材料的Maxwell Beard模型［9］，Phong于1975提出基于经验模型且主要在计算机图形学中作为光照模拟的Phong模型［10］，Ove Steinvall于2000年提出能够很好地描述许多不同类型材质的单站散射特性的四参数单站BRDF模型［11］，吴振森等人于2002年对Torrance-Sparrow模型进行修正，将粗糙表面的高度起伏分布和斜率分布推广到非高斯分布提出五参数半经验统计模型［12］，Sun Yinlong于2007年提出基于微面元高斯分布统计概率而建立的，可以很好地匹配光滑表面和粗糙表面的Sun BRDF模型［13］，等等。

其中Davies理论模型基于电磁场Maxwell方程，其物理意义明确且应用范围相对较广［14，15］，因此本文采用Davies模型研究粗糙面光散射特性。本文首先介绍了描述散射特性的BRDF及Davies理论模型，然后应用Davies理论模型计算了粗糙面的BRDF进而分析得到了粗糙面的散射特性和规律。

1 理论模型

1.1 BRDF

BRDF是描述表面散射特性的一种方式，其定义为［16］:

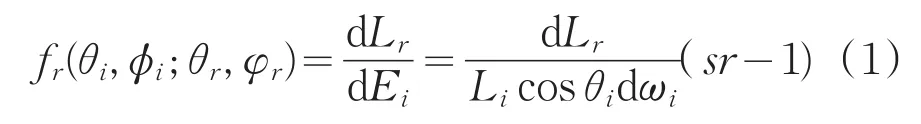
如图1所示，θi和θr为入射和出射天顶角，φi和φr为入射和出射方位角，公式（1）中dEi表示入射光在目标面元造成辐照度的增量，dLr表示该面元在接收到这个辐照亮度增量后在出射方向亮度的增量。Li表示入射辐射亮度，dωi为入射立体角。即BRDF为对于样品表面某一待分析的微面元，其沿出射方向（θr,φr）（探测方向）的亮度增量与引起此亮度增量的入射方向（θi,φi）照度增量的比值。

图1 出射入射光束的几何示意图

1.2 Davies理论模型

Davies理论模型主要是通过假设不规则表面的高度起伏在其平均值附近呈高斯分布，并基于基尔霍夫近似来描述电磁能量从粗糙表面散射的数学公式。其适用于条件下的反射，式中σ为表面粗糙度均方根，a为表面自相关长度［17］。模型的BRDF包含两个部分，分别是镜面反射部分和非镜面反射部分。

其中镜面反射部分表示为:

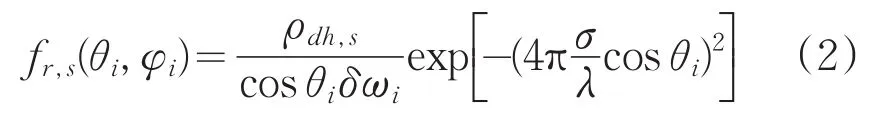
非镜面反射部分表示为:

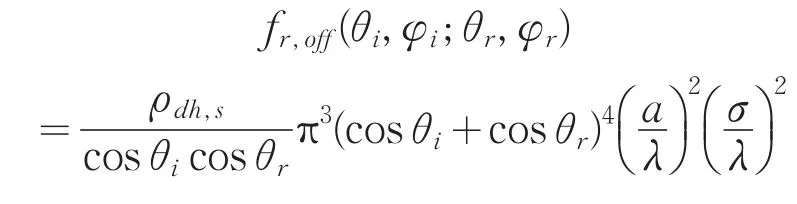
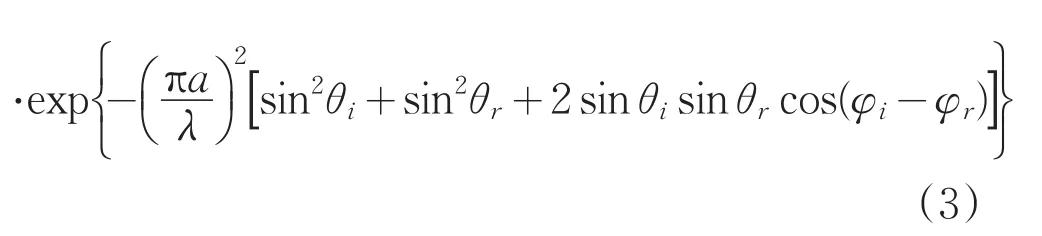
式中，ρdh,s是平滑表面的方向半球反射率，可由菲涅尔公式决定［14］。

假定φi=0∘，θi=30∘，λ=500nm，ρdh,s=28.70%，σ=0.07μm，a=2.2μm，计算取定参数［15］后粗糙表面Davies理论模型的BRDF，其散射形态如图2所示。

图2 粗糙表面Davies理论模型的散射形态图

图2在直角坐标系下，待研究散射材料平放于xOy面上。入射光从图中箭头方向入射（θi=30∘，φi=0∘）。设A(x,y,z)为图形表面上一点，O为原点，可有向量其中θr，φr标示r→（即 OA）向量的方向，同时也为fr(θi,φi;θr,φr)中的出射方向，分别为天顶角和方位角。的大小也同时表示这个出射方向下的 fr值。

由图2可见，粗糙面Davies理论模型形态上表现为一定的类镜面散射特性。由于粗糙面Davies理论模型分为镜面反射部分和非镜面反射部分，镜面反射部分只有镜面反射方向存在散射光，所以在图中镜面反射方向点处 fr函数不连续，出现极窄的尖峰，也就是出现“高光”区域［18］。

2 结果与分析

由公式（2）和（3）可知，因变量有θi，φi，θr和φr参变量有λ（波长），ρdh,s（方向半球反射率），σ（表面粗糙度均方根）和a（表面自相关长度）。假定φi=0∘，θi=30∘，λ=500nm，ρdh,s=28.70%，σ=0.07μm，a=2.2μm，计算取定参数［15］后粗糙表面Davies理论模型的BRDF散射形态如图2。

由于研究参数对于BRDF的影响首先得选定其他参数的值。这里波长选取中间值500nm。方向半球反射率、表面粗糙度均方根和表面自相关长度选取Kapon样品的参数值ρdh,s=28.70%（对应波长500nm下的值）、σ=0.0700μm和a=2.2000μm［15］。

2.1 Davies理论模型中入射角度的影响

假定φi=0∘，λ=500nm，ρdh,s=28.70%，σ=0.07μm，a=2.2μm后，计算粗糙表面Davies理论模型的BRDF散射形态，不同入射角下BRDF散射形态如图3，可见在入射天顶角增大时，非镜面反射部分的形态保持基本不变的同时整体缩小，而镜面反射部分则逐渐增强。由于整体形态基本不变，所以下面讨论随其他参数的影响规律时取入射天顶角θi=30∘这一定值，又由于模型本身假定材料并无方向性，所以入射方位角取任一值均可，为方便起见这里取φi=0∘。

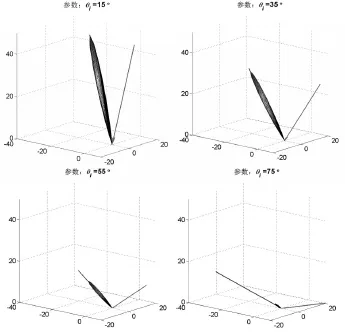
图3 Davies理论模型 fr随θi变化关系图（参数：φi=0∘；λ=500nm；ρdh,s=28.70%；σ=0.07μm；a=2.2μm）

2.2 Davies理论模型中λ及ρdh,s的影响

波长λ对于粗糙表面Davies理论模型的BRDF的影响，从公式本身来说，可以先探讨取定其他参数后 fr随波长λ的变化关系，假定φi=0∘，θi=30∘，ρdh,s=28.70%，σ=0.07μm，a=2.2μm后，计算粗糙表面Davies理论模型的BRDF散射形态，不同入射角下BRDF散射形态如图4。

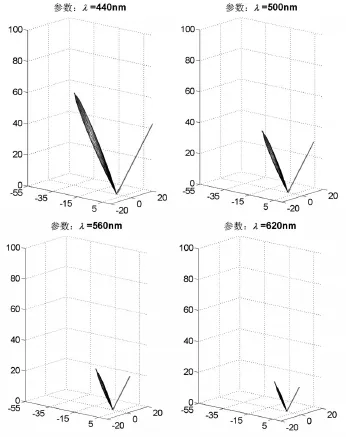
图4 Davies理论模型 fr随λ变化关系图（ρdh,s=28.70%）（参数：φi=0∘；θi=30∘；ρdh,s=28.70%；σ=0.07μm；a=2.2μm）

由公式（2）和（3）可见，如果其他参数均不变，则随着波长λ增长，镜面反射部分逐渐增强；而非镜面反射部分则分为系数部分和指数部分，系数部分逐渐减弱，指数部分逐渐增强，整体的结果则是逐渐减弱。随波长的具体变化关系如图5所示。

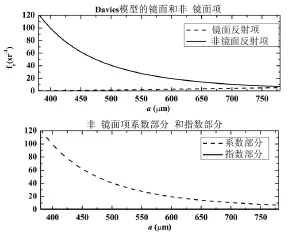
图5 Davies理论模型各项值在镜面反射方向随波长的关系（参数：φi=φr-180∘=0∘；θi=θr=30∘；ρdh,s=28.70%；σ=0.07μm；a=2.2μm）

从图5中可见，Davies理论模型在波长较短时，模型中非镜面反射项起主要作用。随着波长的增大，非镜面反射项的值整体在下降，镜面反射项的值则缓慢增长，所以镜面反射项的作用将逐渐增强。这主要是由于随着波长的增大，粗糙面相对波长的粗糙情况越来越小，从而散射中非镜面项的比重越来越小了。

从Davies理论模型公式出发，可以人为讨论只改变波长而其他参数均不变的情况下的影响规律。但是，参数中方向半球反射率ρdh,s并非与波长λ无关的参数，对于某一确定的材料将ρdh,s=ρdh,s(λ)，本文选取Kapon样品为例讨论，其ρdh,s(λ)随波长λ取值如表1。

表1 Kapon样品ρdh,s(λ)随λ的关系［15］

所以实际上针对已知的特定研究材料，ρdh,s不再是独立参变量，这时假定 φi=0∘，θi=30∘，σ=0.07μm，a=2.2μm，计算粗糙表面Davies理论模型的BRDF，其散射形态如图6。

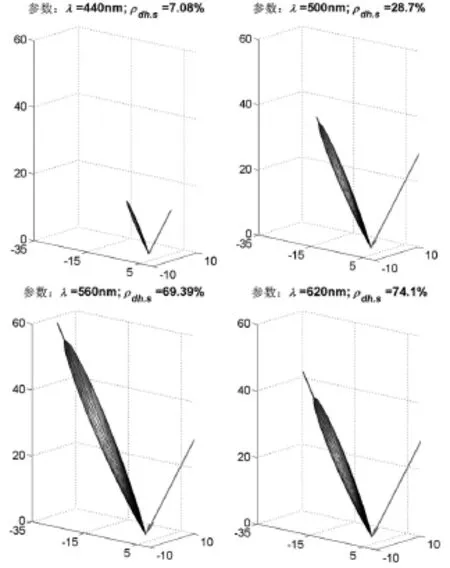
图6 Davies理论模型 fr随λ变化关系图（ρdh,s=ρdh,s(λ)）（参数：φi=0∘；θi=30∘；σ=0.07μm；a=2.2μm）

图6与图4对比可见，当考虑ρdh,s=ρdh,s(λ)后，散射整体形态随波长由递减转化成了先增大后减小关系，而这个转变主要由于ρdh,s在模型中对整个散射起到整体缩放的作用。从而，由于ρdh,s在短波段过渡到中间波段时有快速增大过程而后基本保持不变，使得原本单调递减的整体散射形态在短波段到中间波段有了递增，而后ρdh,s基本不变整体形态又出现再次递减。

2.3 Davies理论模型粗糙面参数的影响

2.3.1 Davies理论模型σ的影响

表面粗糙度均方根σ是表面轮廓高度起伏的标准差，其值大体反映了表面轮廓起伏的高低。图7展示假定φi=0∘，θi=30∘，λ=500nm，ρdh,s=28.70%，a=2.2μm后，计算粗糙表面Davies理论模型的BRDF在不同表面粗糙度均方根σ下散射形态，随着表面粗糙度均方根σ增大，表面轮廓起伏越来越大，表面也越粗糙，所以镜面反射项逐渐减小，而非镜面反射项逐渐增大。

图7 Davies理论模型fr随σ变化关系图（参数：φi=0∘；θi=30∘；λ=500nm；ρdh,s=28.70%；a=2.2μm）

选取镜面反射方向（θr=30∘，φr=180∘）的 fr进行更为具体的分析，如图8可见随着表面粗糙度均方根σ的增大，fr逐渐由镜面反射部分为主逐渐转变为非镜面反射部分为主。

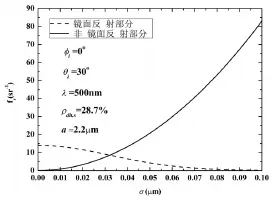
图8 镜面反射方向下 fr随σ变化关系图

2.3.2 Davies理论模型a的影响

表面自相关长度a，是表面自相关函数R(τ)下降到其最大值的倍的τ［17］。一般用来估计随机表面的特征波长，如果轮廓上两点的距离大于自相关长度，则可以认为这两点是互不相关的，用来说明表面轮廓的随机性。

假定φi=0∘，θi=30∘，λ=500nm，ρdh,s=28.70%，σ=0.07μm后，计算粗糙表面Davies理论模型的BRDF在不同表面自相关长度a下散射形态由图9可见，随着表面自相关长度a增大，非镜面反射项逐渐增大。从公式（2）可见，表面自相关长度a并不影响镜面反射项。图10则选取镜面反射方向（θr=30∘，φr=180∘）的 fr进行更为具体的分析。

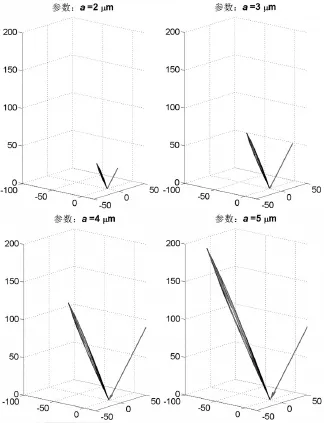
图9 Davies理论模型 fr随a变化关系图（参数：φi=0∘；θi=30∘；λ=500nm；ρdh,s=28.70%；σ=0.07μm）

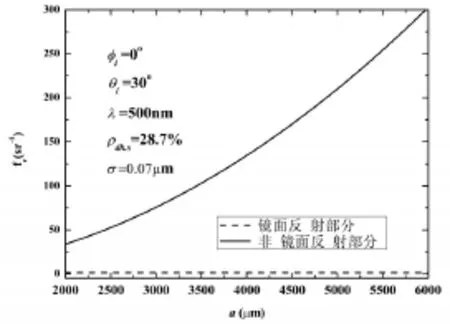
图10 镜面反射方向下 fr随a变化关系图

3 结论

基于Davies理论粗糙面的光散射形态表现出类散射特性，有较强的方向散射特性，其BRDF包含镜面反射项和非镜面反射项，BRDF在镜面反射方向出现“高光”区域。

入射方位角不影响BRDF的整体散射形态和大小，随着入射天顶角的增大，镜面反射部分逐渐增强，非镜面反射部分逐渐减弱。在不考虑方向半球反射率随波长变化时，波长增大主要通过影响非镜面反射部分的系数部分使其逐渐减弱，而镜面反射部分则缓慢增强。在考虑方向半球反射率随波长变化时，方向半球反射率相当于对镜面和非镜面部分整体进行缩放。

表面粗糙度均方根和自相关长度增大都会使Davies理论模型的非镜面反射部分增强，而前者增大使镜面反射部分减弱，后者不影响镜面反射部分。

［1］ 于昊.散射法表面粗糙度测量的数学模型分析［J］.长春理工大学学报:自然科学版，2006，29（1）:109-112.

［2］ 任智斌，姜会林，付跃刚，等.微球体与微椭球体光散射特性的研究［J］.长春理工大学学报:自然科学版，2006，29（1）:28-31.

［3］ 郭立新，王蕊，吴振森.随机粗糙面散射的基本理论与方法［M］.北京:科学出版社，2010:1-4.

［4］ Nicodemus F E.Geometrical considerations and nomenclature for reflectance［J］.Applied Optics，1970，9（6）:1474-1475.

［5］ 孙成明，赵飞，袁艳.基于光谱的天基空间点目标特征提取与识别［J］.物理学报，2015，64（3）:034202-1-7.

［6］ Shen Y J，Zhang Z M，Tsai B K.Bidirectional reflectance distribution function of rough silicon wafers［J］.International Journal of Thermophysics，2001，22（4）:1311-1326.

［7］ 刘宏，朱京平，王凯.基于随机表面微面元理论的二向反射函数几何衰减因子修正［J］.物理学报，2015，64（18）:184213-1-6.

［8］ Torrance K E，Sparrow E M.Theory for off-specular reflection from roughened surfaces［J］.Journal of the Optical Society of America，1967，57（9）: 1105-1114.

［9］ Maxwell J R，Beard J，Weiner S，et al.Bidirectional reflectance model validation and utilization［R］.Ann Arbor:Environmental Research Institute of Michigan，1973:10-35.

［10］ Bui Tuong Phong.Illumination for computer generated pictures［J］.Communications of ACM，1975，18（6）:311-317.

［11］ Ove Steinvall.Effects of target shape and reflection on laser radar cross sections［J］.Applied Optics，2000，39（24）:4381-4391.

［12］ Wu Zhensen，Xie Donghui，Xie Pinhua，et al.Modeling reflectance function from rough surface and algorithms［J］.Acta Optica Sinica，2002，22（8）: 897-901.

［13］ Sun Yinlong.Statistical ray method for deriving reflection models of rough surfaces［J］.Journal of theOpticalSociety ofAmerica，2007，24（3）: 1105-1114.

［14］ Shen Y J，Zhang Z M，Tsai B K，et al.Bidirectional reflectance distribution function of rough silicon wafers［J］.International Journal of Thermo physics，2001，22（4）:1311-1326.

［15］ Bai Lu，Wu Zhensen，Cao Yunhua，and Huang Xun. Spectral scattering characteristics of space target in near-UV to visible bands［J］.Optics Express，2014，22（7）:8515-8524.

［16］ Dai Yongjiang.Laser Radar Technology［M］.Publish House of Electronics Industry，Beijing:2010: 409-412.

［17］ 袁长良，丁至华，武文堂.表面粗糙度及其测量［M］.北京:机械工业出版社，1989:16-17.

［18］ 黄冰峰.物体表面反射特性测定方法的研究［D］.武汉:华中科技大学，2007:8-9.

Study on Scattering Characters of the Rough Surface Based on Davies Theory

WANG Yaodong，CHEN Guibo，ZHANG Ye，HAN Ying，TAN Yong，CAI Hongxing
（School of Science，Changchun University of Science and Technology，Changchun 130022）

In this paper，regularity of scattering has been investigated using BRDF based on Davies theory changing with angle，wavelength，roughness，etc.The numerical simulation showed that the shape of rough surface scattering has a certain scattering of mirror-like and has a highlight area in the specular reflection direction.The scattering shape will be more like specular reflection with the zenith angle of incident increase.The off-specular component will be more important with the wavelength decrease，relative roughness increase，in Davies model.This article research results can provide necessary theory and guidance for complex entity scattering.

Davies theory；BRDF；rough surface

O436

A

1672-9870（2016）05-0045-06

2016-04-12

王耀东（1990-），男，硕士研究生，E-mail:gannannu@163.com

陈桂波（1979-），男，副教授，E-mail:guibochen@126.com