考虑静态电压稳定性的分布式电源优化布置研究

彭光斌李 阳黄培东

（1.西华大学电气与电子信息学院，成都 610039；2.国网四川大邑县供电有限责任公司，成都 611300）

考虑静态电压稳定性的分布式电源优化布置研究

彭光斌1李 阳2黄培东1

（1.西华大学电气与电子信息学院，成都 610039；2.国网四川大邑县供电有限责任公司，成都 611300）

为了研究在考虑静态电压稳定性情况下，配网中分布式电源的优化布置问题。基于IEEE 33节点配电网络和Matlab仿真测试软件平台，以分布式电源（Distributed Generation，DG）接入总容量最大为目标函数，以静态电压稳定指标L（Voltage Stability Index）为约束条件，应用自适应粒子群算法（Adaptive Mutation Particle Swarm Optimization Algorithm，AMPSO）对配电网络中DG的选址和定容进行优化。优化结果得出了配电网络中最优的DG布置方案，同时满足了配电网络电压稳定和分布式电源容量最大的要求，该研究对配网中分布式电源的规划提供了积极的指导意义。

分布式电源；配电网络；静态电压稳定指标；自适应粒子群算法；IEEE 33节点；Matlab仿真软件

分布式电源作为传统集中式大电网发电系统的补充，已经成为现代能源发电系统中不可或缺的部分。但DG的引入使得配网系统从放射状无源网络变为分布有中小型电源的有源网络，电网系统运行的安全可靠性受到极大的影响。文献[1]从经济性、可靠性和安全性三个方面建立了综合指标评价体系，考察分布式电源并网后可能对电网产生的影响。文献[2-3]也是对配网中分布式电源进行优化运算，但是都是针对算法本身进行改进，没有考虑容量最大接入问题。文献[4]分析了DG对配电网电压分布和线路潮流的影响以及分布式电源并网位置和功率因数对准入容量的影响，但没有考虑电压稳定性问题。文献[5-6]应用配电网络负荷增长策略对DG整个系统的静态电压稳定性进行了定量分析，可实现全网薄弱节点的准确定位，也没有考虑DG接入容量最大。

由于上述研究中没有给出配电网络最优DG布置方案中的最大容量确定方案，所以本文基于IEEE 33节点配电网络，应用自适应粒子群优化算法，对配电网中的DG选址和定容进行优化，确定配电网络能够接入的最大容量，并且保证了静态电压稳定性，研究结果对配电网中分布式电源的接入和规划具有积极的指导意义。

1 自适应变异粒子群算法

Kennedy和 Eberhart提出的一种基于鸟类群体智能搜索的随机演化计算方法，粒子群优化（Particle Swarm Optimization，PSO）算法，对求解大规模优化问题有很快的收敛速度和全局寻优能力[7]。

在每一次迭代过程中，各粒子根据如下公式更新自己的速度和位置，即

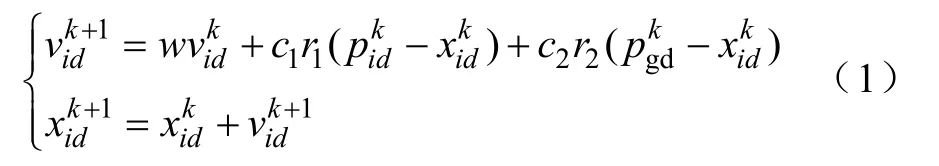
惯性权重w使粒子保持运动的惯性，使其有扩展搜索空间的趋势，有能力搜索新的区域。本文采用自适应的粒子群算法调整 w，使其随算法迭代而线性地减少[8]，即

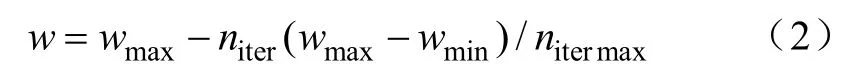
式中，wmax、wmin分别为惯性权重的最大值和最小值；niter为当前迭代次数；nitermax为最大迭代次数。

基本粒子群算法结构相对简单，运行速度快，但容易陷入局部最优。鉴于此，本文在算法运行过程中根据群体适应度方差以及当前最优解的大小来确定当前最优粒子的变异概率[9]。变异操作增强了粒子群优化算法跳出局部最优解的能力，能有效避免早熟问题。

由于各粒子的位置可通过适应度值来体现，因此，通过分析群体中所有粒子适应度值的整体变化来实现对各粒子“聚集”程度的定量描述。群体适应度方差为

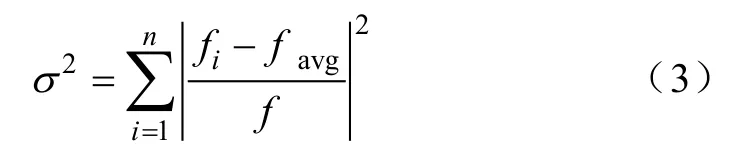
式中，n为粒子群体规模；fi为第 i个粒子的适应度值；favg为粒子群体目前的平均适应度；σ2为粒子群的群体适应度方差；f是归一化定标因子，用于限制σ2的大小，可利用如下公式计算

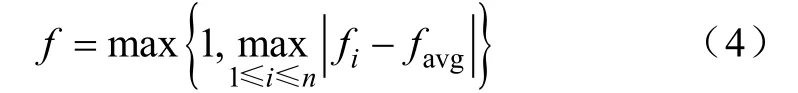
式（4）表明，群体适应度方差σ2反映了粒子群的“收敛”程度： σ2越小，则粒子群趋于收敛；反之，粒子群则处于随机搜索阶段。

为了使算法在陷入搜索停滞时保证各粒子朝新的方向搜索，根据群体适应度方差σ2的大小确定变异概率Pk[10]的大小：

式中，Pk为第k次迭代中群体全局最优的变异概率；为第k次迭代中群体的适应度方差；分别为变异概率的最大值和最小值。

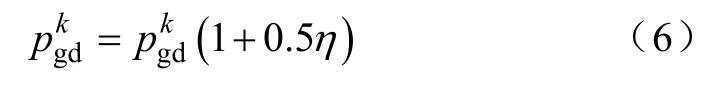
式中，η为服从Guass(0,1)分布的随机变量。

2 仿真测试

2.1 测试系统

本文基于 IEEE 33节点配电网[12]进行仿真测试，该系统电压等级为 12.26kV，总有功负荷为3715kW，总无功负荷为 2300kvar，基准容量取10MVA。

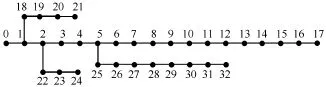
图1 IEEE 33节点辐射配电网测试系统

2.2 参数设置

设置每个节点接入容量为 m*60，m为容量比例，60kVA为容量基数。29节点的容量最大为632.46kVA，为保证每个节点接入的DG容量处于可控范围，每个节点接入最大容量比例为 10，即10*60kVA。根据DG接入总容量不超过上一级总负荷的25%，则单个DG最大容量为1092.34kVA，系统接入总的DG容量也不能超过1092.34kVA，即系统最多接入容量18*60kVA。

粒子群优化算法中参数选取如下：学习因子c1=2和c2=2，惯性权重最大值wmax=0.9，最小值wmin=0.4，最大速度vmax=4，种群规模N=30，最大迭代次数 nitermax=50，变异概率最大值Pmax=0.5和变异概率最小值Pmin=0。

2.3 仿真结果

原始配电网各节点电压的分布情况如图2所示。

图2 原始配电网各节点电压的分布

原始配网各支路的静态电压稳定指标L的分布情况如图3所示。

图3 原始配网各支路的静态电压稳定指标L的分布情况

可以看到，支路5的L值最大，为系统最不稳定支路，以它作为整个系统静态电压稳定性的判断基准。

最优DG布置方式和最大接入DG容量，优化结果见表1。

DG接入最大容量历代优化曲线如图4所示。

可以看到，改进的自适应粒子群算法优化，随着迭代次数的增加，配电网络中能够接入的分布式电源的总容量逐渐趋于稳定，最后稳定在1080kVA。

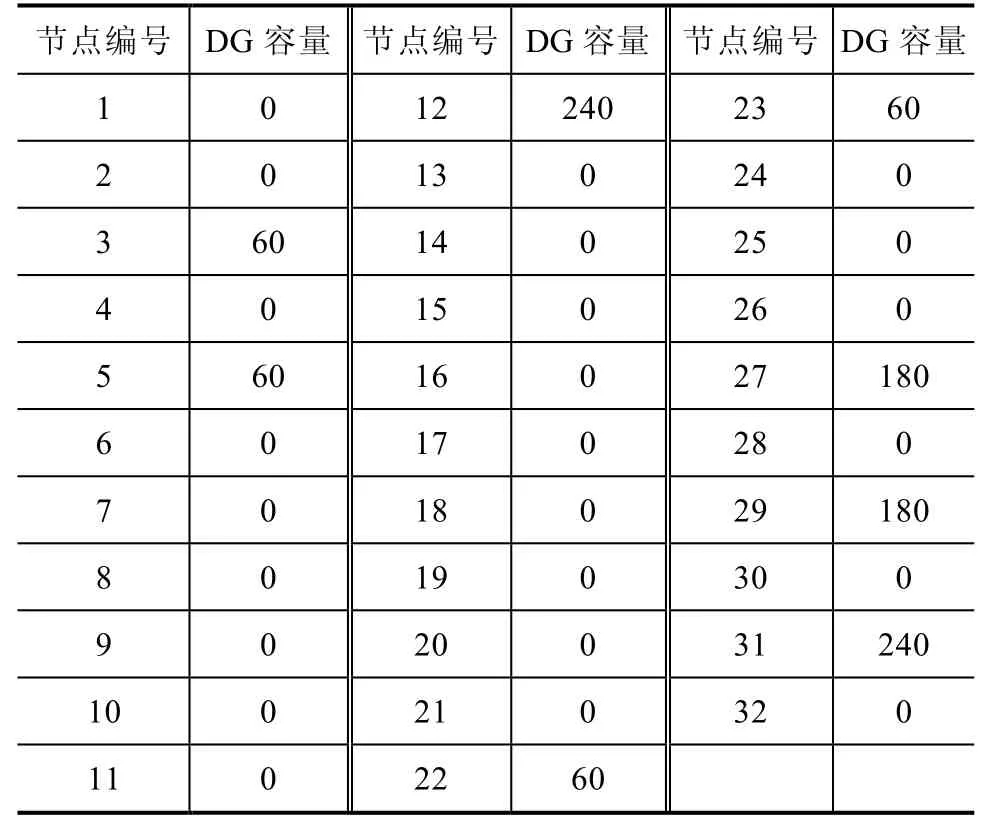
表1 最优DG布置方式

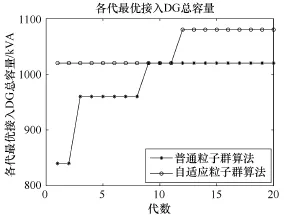
图4 最大DG容量优化曲线的两种算法对比

对比普通粒子群算法和自适应改进粒子群算法的寻优仿真，可以看到，前者寻优得到的最大 DG总容量稳定在1020kVA，并不是真正的最大容量，陷入了局部最优。而自适应粒子群算法跳出了局部最优值，得到最优值1080kVA。这正是由于自适应粒子群算法中加入变异操作带来了更优的全局寻优能力，该优化算法具有更强的优化效果。

历次迭代系统最大L指标maxL记录如表2所示，其中 maxL表示每次迭代后，系统中所有支路中L指标最大值。

其对应的迭代寻优曲线如图5所示。

由仿真图可以明显看到，利用自适应粒子群算法的寻优得到的最大静态电压稳定指标 maxL为0.151080，具有更理想的结果。相比下，普通粒子群算法只寻得的值 maxL稳定在 0.151588，是局部最优值。证明改进的自适应粒子群算法的可行性和正确性。

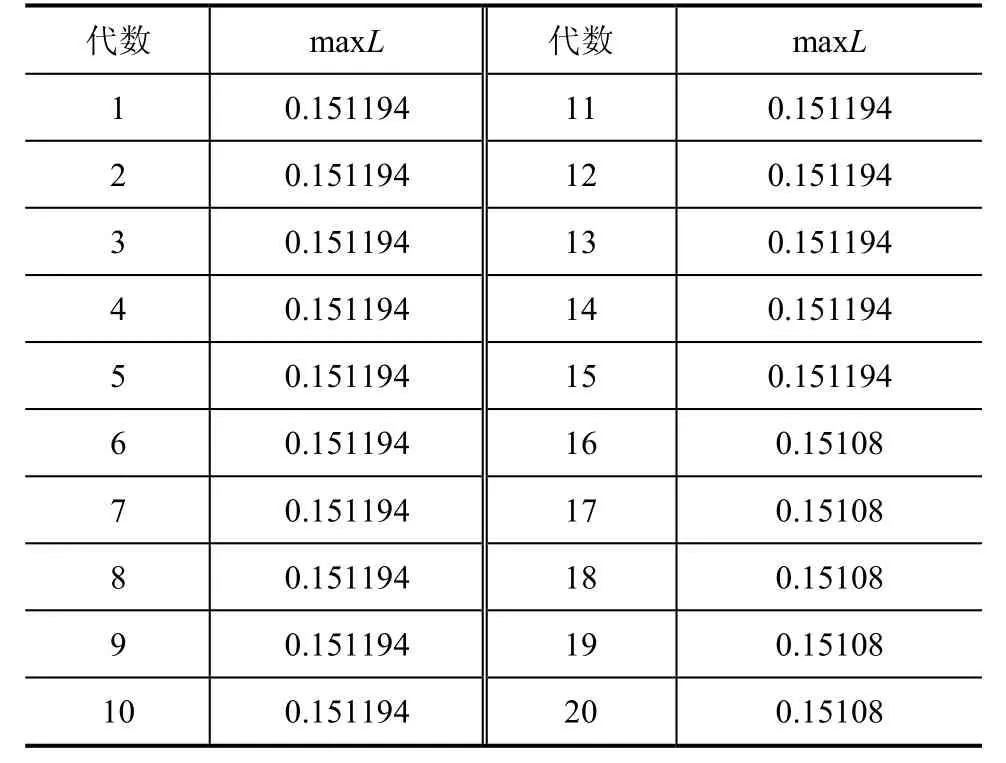
表2 历次迭代系统最大L指标maxL

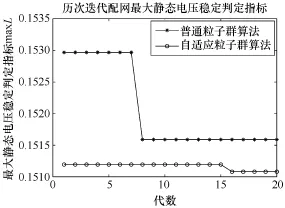
图5 两种算法下的系统最大静态电压稳定判定指标maxL迭代对比曲线

最优DG布置方式下配网系统的静态电压稳定指标L如下表3所示，其中L指标表示系统各支路的静态电压稳定指标L，|L−1|越大，支路越稳定。

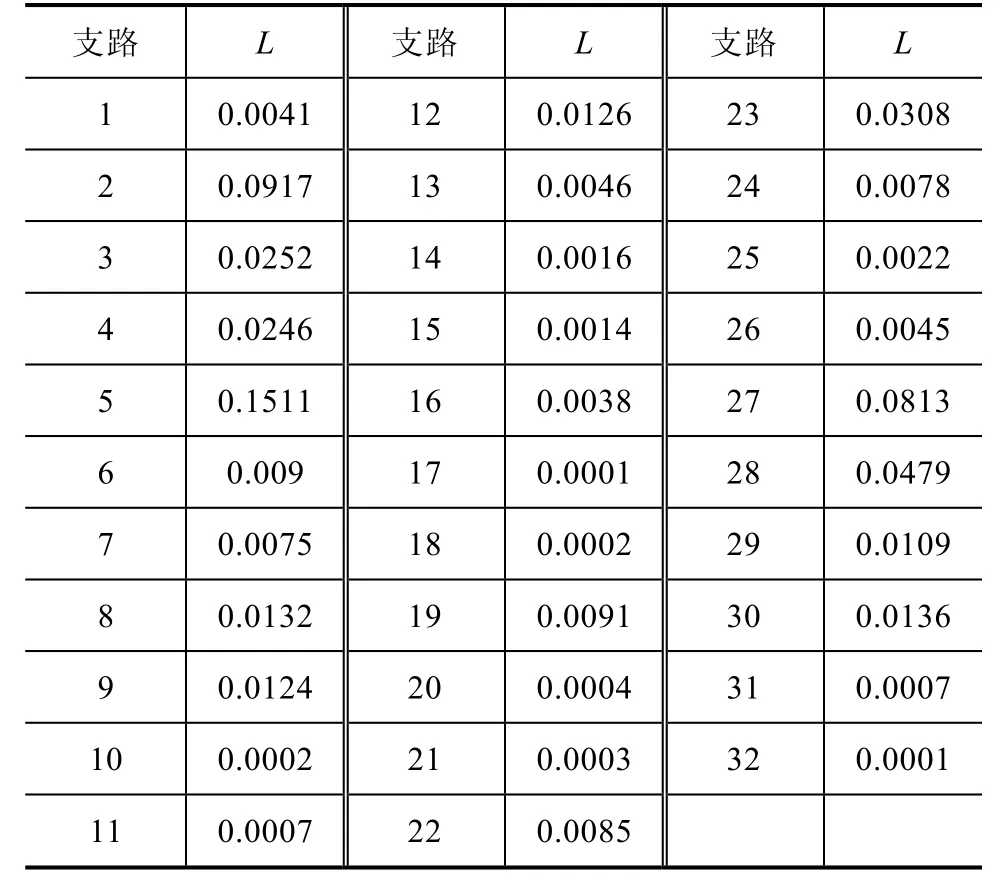
表3 最优DG布置方式下配网系统的静态电压稳定指标L

原始网络和最优迭代DG布置下电压稳定指标L对比，如图6所示。

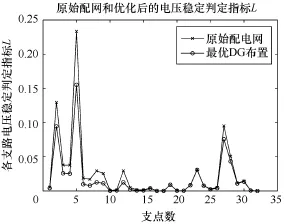
图6 原始网络和最优迭代DG布置下L指标

可以看到，通过优化，系统各支路的L指标都比原始配电网的L指标小，说明支路稳定性改善了。同时，原配电网最不稳定的支路5的L值明显降低了，所以整个系统的静态电压稳定性是得到提高的。

2.4 结果分析

首先，每次迭代后，新的DG布置方式下，各节点的电压波动百分比的绝对值要低于7%，电压不能越限。其次，每次迭代过程中，除了各支路的 L指标都要比1小，不能失稳以外，而且要保证系统最大的L指标maxL2都比上一代的小，这样整个系统的静态电压稳定性是得到提高的。同时对比了两种算法的优化效果，仿真测试结果符合预期的目标，得到最优DG布置方式，DG接入最大接入总容量为1080kVA。

3 结论

通过仿真测试，达到预期的目标要求，并得到以下结论：

1）分布式电源的接入，可以改善系统的静态电压稳定性，但是对于DG的接入位置和容量必须合理安排。

2）通过配网最大静态电压稳定指标，可以快速的判断系统最不稳定支路。maxL作为系统静态电压稳定判定的重要指标，保证最不稳定支路不失稳，能够有效提高整个配网的稳定性。

3）论文中的仿真测试方案，能够对分布式电源的注入容量进行优化，让DG接入配电网的容量最大化，同时改善系统电压稳定性，为分布式电源接入配电网对电压稳定性的影响研究提供积极的指导意义，具有一定的借鉴和参考价值。

[1]柳睿,杨镜非,程浩忠,等.分布式电源并网的综合评价[J].电力系统及其自动化学报,2013,25(1):34-39.

[2]康鲁豫,朱顺,刘刚.考虑电压稳定和网损的分布式电源最优选址和定容[J].电气技术,2015(2):1-5,22.

[3]徐卫星.基于改进粒子群算法的分布式电源优化配置[J].电气技术,2015(12):71-75.

[4]夏成军,崔弘,王强,等.考虑静态安全约束的分布式电源准入容量计算[J].电网技术,2009,33(16):96-100.

[5]张谦,廖清芬,唐飞,等.计及分布式电源接入的配电网静态电压稳定性评估方法[J].电力系统自动化,2015,39(15):42-48.

[6]陈海焱,段献忠,陈金富.分布式发电对配网静态电压稳定性的影响[J].电网技术,2006,30(19):27-30.

[7]Kennedy J,Eberhart R.Particle swarm optimization[C]//Proceedings of IEEE International Conference on Neural Networks,1995:1942-1948.

[8]叶德意,何正友,臧天磊.基于自适应变异粒子群算法的分布式电源选址与容量确定[J].电网技术,2011,35(6):155-160.

[9]王江海,邰能灵,宋凯,等.考虑继电保护动作的分布式电源在配电网中的准入容量研究[J].中国电机工程学报,2010,30(22):37-43.

[10]Shi Y,Eberhart R.A modified particle swarm optimizer[C]//Proceedings of IEEE International Conference on Evolutionary Computation,1998:69-73.

[11]刘世成,张建华,刘宗岐.并行自适应粒子群算法在电力系统无功优化中的应用[J].电网技术,2012,36(1):108-112.

[12]Baran M E,Wu F F.Network reconfiguration in distribution systems for loss reduction and load balancing[J].Power Engineering Review,IEEE,1989,9(4):101-102.

The Research of the Optimization Allocation of Distributed Generation with Static Voltage Stability Index Considered

Peng Guangbin1Li Yang2Huang Peidong1
(1.School of Electrical Engineering and Electronic Information,Xihua University,Chengdu 610039;2.Dayi Sichuan Power Supply Co.,Ltd,Chengdu 611300)

In order to research the optimization allocation of Distributed Generation in distribution network with the static voltage stability index considered.The platform of Distribution Network of IEEE 33 nodes and Matlab simulation software based on the Distributed Generation in a total capacity of maximum as the objective function,the static voltage stability index L as the constraint conditions,using the adaptive particle swarm optimization algorithm of DG in Distribution Network location and sizing optimization.The conclusions obtained from the test system satisfy the static voltage stability index and the Maximum capacity of DG,which may be available for distributed generation connecting and planning in distribution networks.

distributed generation;distribution network;static voltage stability index;adaptive mutation particle swarm optimization algorithm;IEEE 33 nodes;Matlab simulation software

彭光斌（1990-），男，四川达州人，硕士研究生，从事电力系统继电保护及分布式电源并网电压稳定性问题的研究工作。