智能变电站数字采样下双重插值算法对高次谐波测量精度的影响

刘永钢 陈桂友 熊慕文

（南京南瑞继保电气有限公司，南京 211102）

智能变电站数字采样下双重插值算法对高次谐波测量精度的影响

刘永钢 陈桂友 熊慕文

（南京南瑞继保电气有限公司，南京 211102）

智能变电站数字化采样之后，间隔层二次设备需要对合并单元发送的SV采样数据作同步插值处理。为实时跟踪测量电力系统的运行频率，计算模块需要通过插值重构的算法进行重采样。为分析双重化插值带来的误差影响，本文详细分析了拉格朗日和牛顿插值算法的理论最大误差，对高次谐波的精度影响进行了量化分析和补偿计算。最后提出了进一步提高插值算法下高次谐波测量精度的思路和方法。

数字化采样；双重插值；误差分析；谐波补偿

随着智能变电站的推广和电子式互感器、IEC 61850标准的应用，变电站内电压量、电流量的采集均通过合并单元和过程层采样值（Sampled Value，SV）网络实现数字化采样。由于站内电压、电流一般是分布式采集的，需要对不同合并单元的采样数据进行同步[1]。目前多采用脉冲同步法或者插值同步的方法[2]。此外合并单元发送的数据为M点（80点）每周波，而计算时一般都会插值抽取为N点（24点或48点），因此合并单元的采样数据在进入装置的数字信号处理（Digital Signal Processing，DSP）计算之前都要经过第一重插值算法的处理。

实际运行的电力系统其频率不是固定在 50Hz不变的，而是在一定的范围内（45～60Hz）正常波动。为实现对运行系统遥测量的准确测量，保护或者测控装置一般采取调节采样中断间隔或者插值重构的方法进行频率跟踪。国网公司最新颁布的《10kV～110（66）kV线路保护及辅助装置标准化设计规范》中对于110kV及以下电压等级中的保护测控一体化装置，要求保护和测控功能互不影响。因此系统频率变化后保护和测控不可以同时调节装置的采样中断；同时对于集中式测控或者多专业集成的装置，模块之间实现频率跟踪时也会用到插值算法。采样数据进入DSP后计算处理过程中也会涉及到第二重插值算法的处理。

对采样数据同步或是重构，插值算法的合理选取无疑对遥测量的计算精度起着关键的作用。常用的插值算法包括线性插值、拉格朗日插值、分段样条函数插值法以及牛顿插值算法等[3]。线性插值算法实现简单，其误差精度只可以满足基波分量，无法满足高次谐的测量；而分段样条插值算法虽然精度高，但计算量很大且需要具备强大的数据处理能力。本文基于插值算法的误差公式对常用的插值算法进行误差分析，重点探讨双重插值算法下所引入的插值误差对测量精度的影响，并将分析结果应用于后续的数据处理计算中，以满足高次谐波以及计量等对精度要求很高的应用场合。

1 智能变电站中插值算法的应用

根据IEC 61850-9-2的规定，合并单元的采样速率为4K。对于间隔层的保护或者测控装置而言，过程层 SV接收处理模块需要对 SV采样数据进行同步。同时为了降低背板间数据的传输负载以及快速傅里叶变换（Fast Fourier Transformation，FFT）运算的复杂度，一般会把原始的 80点数据抽取为 M点（24/32/48每周波）进行计算，这个过程用到了第一重插值算法。

对于纯测控而言可以根据实测的频率实时调整SV接收单元的采样中断间隔而实现频率跟踪；而对于保护测控一体或者多功能集成装置而言，不可能由多块DSP共同调节装置的采样中断时间，这种情况下必须采取对同步的定频采样数据进行再次插值重构的方式，获得对应频率下每周波固定点数的采样数据，因此从合并单元原始的 4K采样数据到最后计算处理一共经过了双重插值算法的处理，研究双重化插值下对测量精度的影响变得很有必要。

插值算法的原理是根据已知的若干离散采样点构造一个近似的函数表达式，用构造函数表达式来计算未知离散点的实际值。根据选取点数的不同分为线性插值、拉格朗日插值和牛顿插值等，插值原理如图1所示[4]。

图1 插值算法原理

离散后可得差分形式的插值多项式为

插值多项式中对应的插值误差可以用余项表示：

文献[2]中指出电力系统暂态情况下，电流的表达式统一可以表示为直流分量和各次谐波叠加的形式：

结合文献[4]可得插值误差的一般式为

式中，只要求得当t在[0,1]范围内|t( t−1)…(t−n)|的最大值，理论上可以得到不同插值算法下的最大误差值。

2 插值误差分析

插值算法会引入插值误差，第一重插值算法引入的误差越小，第二重插值的时候就越能降低原始波形的失真度。第一重插值处理需要将 4K采样数据同步为48点（考虑到13次谐波的测量精度要求并结合采用定理，本文计算点数采用48点），第二重插值算法需要插值重构达到频率跟踪的目的。考虑到误差的影响以及算法的复杂度，本文选取常用的拉格朗日插值和牛顿插值算法进行分析，其他插值算法的组合也可以采用类似的方法进行估算。

拉格朗日插值算法是一种多项式插值，即用三个离散采样点构造近似的插值函数。对应的插值最大误差表达式为

对误差式（4）求导可知当t=0.423时，对应插值误差取最大值。因此由式（4）可得采用拉格朗日插值算法，其作为一重插值算法和二重插值算法时的各次谐波理论最大误差见表1。

表1 拉格朗日插值算法下各次谐波最大插值误差

牛顿插值算法用多个离散采样点构造插值函数，随着插值阶数的提高其插值误差也越小。考虑到计算复杂度和目前变电站内遥测精度的要求，本例分析4阶牛顿插值算法对应的理论插值误差为

对误差式（5）求导可知当t=0.359时，对应误差取最大值。因此采用4阶牛顿插值算法，作为一重插值和二重插值算法时的各次谐波理论最大误差见表2。

表2 牛顿插值算法下各次谐波最大插值误差

由表2可知采样4阶牛顿插值算法，当采样间隔为每周波48点时仅需要在10次及以上的高次谐波做补偿。

根据上述对拉格朗日和牛顿插值算法的误差理论计算分析，可以得出如下结论：

1）误差表达式中不含有直流分量，即插值算法不会产生直流分量的误差。

2）插值误差是各次谐波误差的线性组合，越高次的谐波对误差的贡献率越大。

3）第一重插值处理时（SV接收处理模块将原始的80点同步插值为48点），采用拉格朗日算法超过6次以上的高次谐波需要补偿；而采用4阶牛顿插值算法则几乎不需要补偿，对13次谐波的测量没有影响。

4）第二重插值处理时，则不能选择拉格朗日插值，只能选取逼近效果更好的4阶牛顿插值。且二重插值导致的高次谐波衰减系数是固定的，经 FFT分解后可以对实部和虚部用固定系数补偿。

5）插值误差分析结果用于插值算法的选择：考虑到前端数据处理的简化以及数据传输的复杂度，第一重插值算法选择拉格朗日算法，即简化运算量又可以满足高次谐波精度要求；而为了满足国网新一代中对非关口计量、测量精度的要求，第二重插值处理采取4阶牛顿插值算法。

3 插值算法下谐波的计算及补偿

根据GB/T 13729标准中规定，测控装置需要满足叠加最高13次谐波20%标称值时，其误差允许改变量最大为200%，即误差极限不能超过0.4%；且新一代智能变电站中要求装置集成非关口计量的功能，精度满足0.5S级。

3.1 谐波补偿算法

本文计算中用到的 DSP为 2片 ADI公司的BF534芯片，主频为375MHz，系统频率125MHz。DSP1用于接收SV原始采样点并采用拉格朗日算法同步为48点；DSP2通过背板总线接收DSP1传送的数据并进行插值重构、谐波补偿以及模拟量计算。原始采样点插值后经FFT分解为对应向量的实部和虚部，对分解后的每次谐波向量做补偿。补偿之后的向量实部和虚部就可以用于后续均方跟（Root Mean Square，RMS）有效值、谐波幅值以及谐波功率的计算。整个计算处理在实时中断任务中执行，DSP的总体负载率为40%左右，实现流程如图2所示。

图2 插值补偿算法实现流程图

对于双重插值算法处理，假设第一重插值算法幅值衰减系数为 k1，第二重插值算法幅值衰减系数为 k2，则理论补偿系数为对FFT分解后的实部和需部分别补充并计算有效值。

3.2 谐波补偿结果分析

根据前面的插值误差分析可知，第一重插值同步过程中，采用拉格朗日插值算法在高于6次谐波时需要补偿，且每一次谐波因插值引起的补偿系数是固定的。同时第二重插值采用4阶牛顿插值算法可以很好地还原原始波形，且二次插值所引起的高次谐波误差也可以通过固定系数补偿。

将采用不同的插值方法所得到的补偿系数做比较如图3所示。三条曲线的点分别代表拉格朗日算法理论补偿系数、拉格朗日一次插值实际补偿系数、拉格朗日+4阶牛顿插值双重插值实际补偿系数。对比结果可知采用拉格朗日插值算法超过6次谐波时需要补偿，这点和理论误差分析是吻合的。同时如果后续采用4阶牛顿插值算法进行二次插值，则同样只需要对高次谐波进行补偿，相比只进行一次拉格朗日插值其补偿系数几乎是吻合的，进一步说明4阶牛顿插值所带来的二次插值误差基本可以忽略，对最终的计算没有影响。

图3 插值补偿系数比较

采用双重插值算法对高次谐波用固定补偿系数补偿之后的最终测试结果见表 3。测试结果表明补偿之后高次谐波最大误差为 0.07%左右，完全满足GB/T 13729中对测控装置谐波测量的精度要求。同时采用这种插值补偿算法之后，将插值数据用于后续功率以及非关口计量的计算，经实际测试也可以满足0.5S级精度要求。

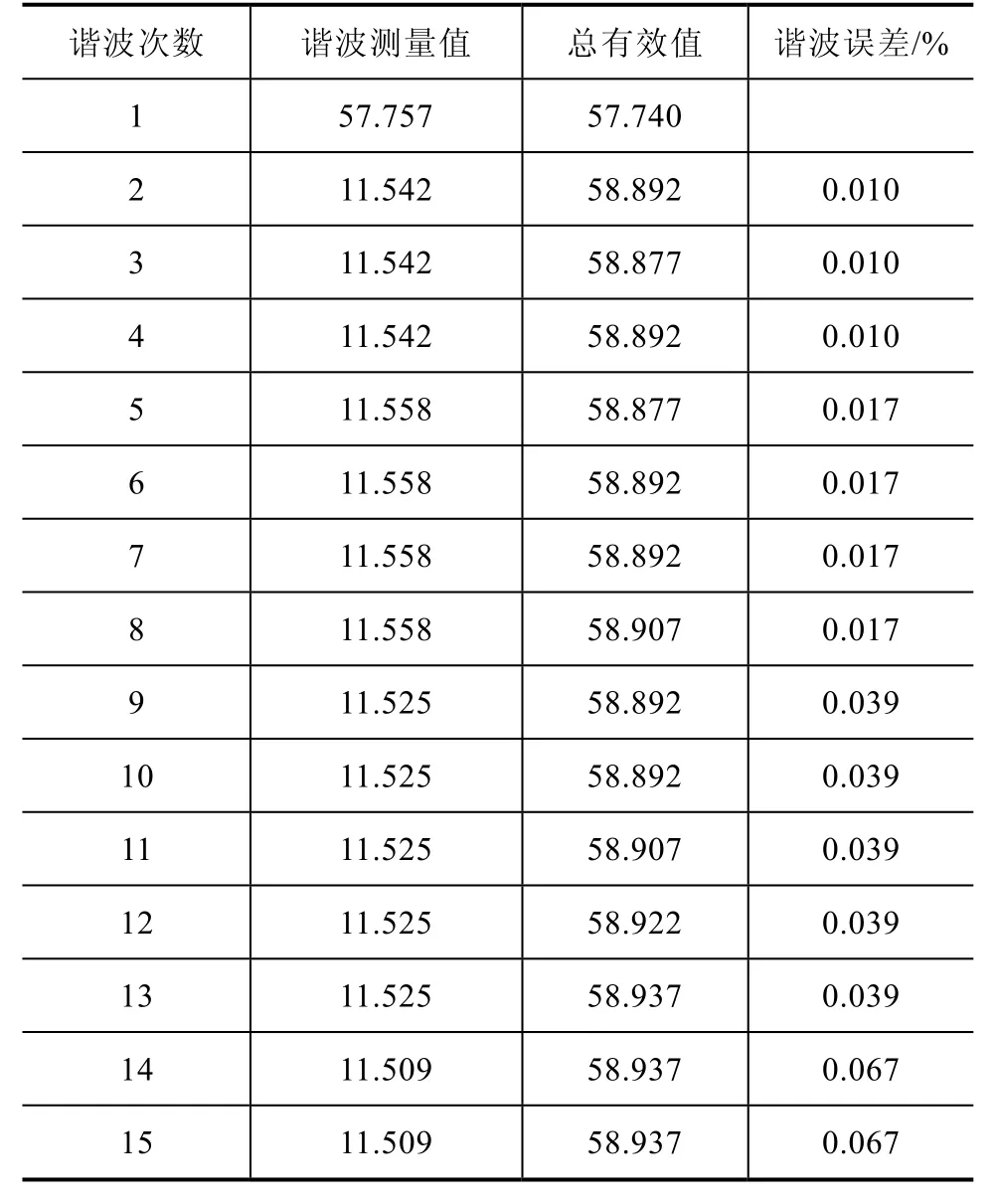
表3 双重插值算法下谐波补偿之后的测试结果

4 结论

随着智能变电站中对于高次谐波测量、非关口计量以及向量测量装置（Phasor Measurement Unit，PMU）等应用的整合趋势，插值处理对于遥测计算的精度影响要求越来越高。本文分析了原始采样数据到最后计算过程中涉及到的双重插值算法，进行了原理介绍和理论误差计算，尤其对高次谐波的精度影响进行了量化分析，并根据分析结果对插值算法下高次谐波进行了软件补偿，补偿之后可以满足现阶段智能变电站对遥测量谐波的测试要求。

毕竟采用插值算法会带来插值误差，后续如果要进一步提高遥测量精度，如满足更高精度要求的计量要求，可以从如下角度考虑，但同时对硬件和软件资源也提出了更高的要求：

1）增大计算点数N，N越大对应的误差越小，但同时也带来了计算量的增加。

2）在数据处理前端采用高阶的牛顿插值代替拉格朗日插值，在数据处理后端减少二次插值。

[1]徐文佳,赵伟,肖勇,等.数字化变电站中实现电压电流同步的合并单元[J].电测与仪表,2015,52(1):1-7.

[2]曹团结,尹项根,张哲,等.电子式互感器数据同步的研究[J].电力系统及其自动化学报,2007,19(2):108-113.

[3]郭乐,潘济猛,卢家力,等.插值算法在智能变电站中的应用[J].电力自动化设备,2010,30(10):103-105,109.

[4]乔洪新,黄少锋,刘勇.基于二次插值理论的电子式互感器数据同步的研究[J].电力系统保护与控制,2009,37(15):48-52.

[5]周斌,鲁国刚,黄国方,等.基于线性Lagrange插值法的变电站 IED采样值接口方法[J].电力系统自动化,2007,31(3):86-90.

[6]蔡超,陆于平,黄涛,等.基于插值和时标变换的智能变电站保护数据重采样算法[J].电力系统自动化,2013,37(19):80-85.

[7]邓建中,刘之行.计算方法[M].西安:西安交通大学出版社,2001.

[8]赵磊,单渊达,李蔚.正弦信号二次插值算法的误差分析[J].继电器,2004,32(13):11-14.

[9]孙蓓俊,李帅,丁泉.智能变电站插值算法研究[J].华电技术,2013,35(11):72-75.

Impact of Dual Interpolation Algorithm for High Order Harmonic’s Measurement Accuracy in Smart Substation

Liu Yonggang Chen Guiyou Xiong Muwen
(NR Electric Co.,Ltd,Nanjing 211102)

With digital sampling in smart substation,sample data synchronization which is sent by the merging unit is necessary for the IEDs.For real-time tracking and measuring the operating frequency of the power system,the sampling data’s resampling is often required by using interpolation algorithm.In order to analyze the error caused by dual interpolation,this paper analyzes the theoretical error of Lagrange and Newton interpolation algorithm,and quantitative analyzes of impact for high order harmonic is provided.The compensation due to interpolation algorithm is calculated according to the analysis.In the end,the method of improving the accuracy of high order harmonic measurement based on interpolation algorithm is proposed.

digital sampling;dual interpolation algorithm;error analysis;harmonic compensation

刘永钢（1984-），男，山西平遥人，工程师，从事变电站自动化系统、数字化变电站系统研发工作。