分布式电源并网逆变器新型滤波器的设计及实现

张玮亚王紫钰

（1.南京供电公司，南京 210019；2.徐州供电公司，江苏 徐州 221000）

分布式电源并网逆变器新型滤波器的设计及实现

张玮亚1王紫钰2

（1.南京供电公司，南京 210019；2.徐州供电公司，江苏 徐州 221000）

为了更好地解决分布式电源并网引起的高频谐波污染问题，本文在详细分析SPWM调制型逆变器开关过程产生的谐波电压的基础上，设计了一种适于滤除此类谐波电压的新型滤波器——双谐振滤波器。与常用的LCL滤波器相比，双谐振滤波器有良好的高频谐波衰减特性，对电感的需求少，大大降低了滤波器的成本和体积。最后给出了双谐振滤波器的实现方法及参数设计原则。PSCAD仿真结果验证了双谐振滤波器的可行性和有效性。

并网逆变器；滤波器设计；SPWM谐波分析；有源阻尼法

分布式电源并网逆变器一般采用SPWM调制，在运行过程中会向接入电网注入大量的高次谐波电流[1]。这类谐波电流不仅会加速电气设备的老化，还会对电力通信传输和电气量测量精度产生影响[2]，因此必须在并网逆变器的输出侧加装滤波器。国内外对于并网逆变器注入电网的高频谐波电流均有严格的要求，基于IEEE Std.519的规定：35次以上各次的谐波电流均要小于额定电流的0.3%[3]。目前分布式电源并网逆变器多采用LCL滤波器[2]，文献[4]提出了一种简易而实用的 LCL滤波器参数设计方法。此外，对LCL滤波器的控制方法的研究也比较深入[4-6]。然而为保证良好的滤波效果，LCL滤波器通常需要较大的滤波电感值，导致LCL滤波器的体积大，成本高，无功损耗也很大。因此设计一个在经济性和滤波特性比LCL滤波器更好的输出滤波器结构依然是一个值得研究的问题。

本文首先分析了采用 SPWM调制的并网逆变器输出的谐波电压分布情况，指出采用LCL滤波器在滤除这类谐波电压时的缺陷。随后提出了一种更适合削减这些谐波电压含量的新型滤波器——双谐振滤波器。最后，提出了抑制双谐振滤波器中正谐振尖峰的策略以及双谐振滤波器的参数设计原则。

1 三相SPWM逆变器输出谐波电压分析

1.1 SPWM逆变器输出谐波电压频率分析

设SPWM逆变电路的调制波频率为fr,开关频率为 fc，通常情况下 fc＞＞fr。在假设输入直流电压源理想和忽略功率开关元件的死区特性的前提下，三相半桥式 SPWM逆变电路的线电压谐波有效值表达式为[7]

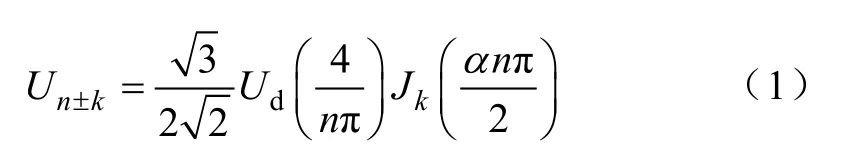
式中，Jk为第一类贝塞尔函数，Un±k代表频率为nfc±kfr的谐波电压有效值，Ud为直流源电压，α为调制比。当n=1,3,5,…时，k=3(2m−1)±1，m=1,2,3,…；当n=2,4,6,…时，k=3(2m+1)±2，m=0,1,2,…。

SPWM逆变器输出的谐波电压主要集中在以fc,2fc,3fc,4fc,…为中心的周围的频段[7]。式（1）中，故当k≥5时，当k≥7时，因此以fc和 2fc为中心的谐波电压U1±k和U2±k只存在于 fc±2fr，fc±4fr，2fc±fr，2fc±5fr等fc和2fc附近的频率上。同时由第一类贝塞尔函数的性质可知：频率为 fc±2fr和 2fc±fr的谐波电压有效值远大于频率为 fc±4fr和2fc±5fr的谐波电压有效值。而n≥3时，使得的k的取值递增[8]，所以谐波电压Un±k的分布随着频率的增加而渐渐分散，不再仅仅集中于nfc附近的几个频率上。

1.2 SPWM逆变器输出谐波电压有效值分析

线电压基波有效值 U0如式（2）所示[9]。通过式（3）到式（6）分别计算出电压有效值U总，谐波电压有效值Uh，fc和2fc附近的谐波电压有效值之和Ufc1与Ufc2，以及剩余所有频段的谐波电压Ure：

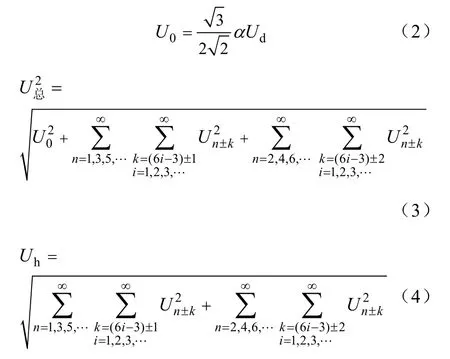
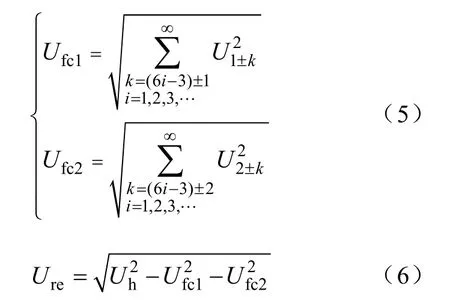
常用的 SPWM 并网逆变器的调制比一般为α=0.7～0.9[1]，图1为当调制比α=0.7～0.9时，依式（1）至式（6）计算出的各频段谐波电压含量。

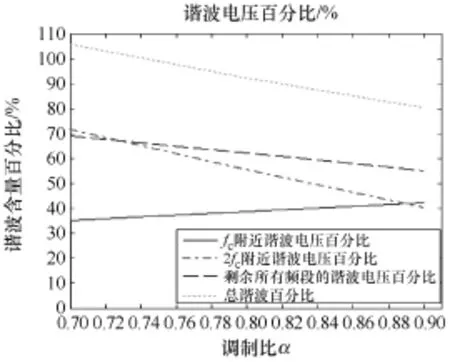
图1 各个频段的谐波电压百分比

由图1可知：三相桥式SPWM输出谐波电压总含量百分比Uh/U0很大，约为80%～110%。谐波电压主要由Ufc1、Ufc2、Ure这3个部分组成：Ufc1/U0在大约35%～45%之间，Ufc2/U0在大约40%～70%之间，Ure/U0在大约60%～70%之间。

图2是当调制比α=0.8，fr=50Hz，fc=1650Hz，Ud=800V时的三相桥式SPWM逆变器输出线电压波形图以及对应傅里叶分析图。由线电压波形图可知，输出的线电压含有大量的高频电压谐波。而从傅里叶分析图可知：fc附近和2fc附近的谐波电压集中于fc±2fr和 2fc±fr处，且含量很高。随着频率增大，谐波电压分布渐渐分散，验证了上文中的分析。

综上所述，SPWM逆变器输出的谐波电压有很大一部分集中在fc附近和2fc附近，其中又以频率为fc±2fr和 2fc±fr的谐波电压为主。其余谐波电压分散在大于 2fc的频段。而且这三类谐波电压含量都很大，SPWM并网逆变器的输出滤波器要对这3类谐波电压都具有很好的衰减能力。

2 新型滤波器的电路设计与分析

分布式电源并网逆变器的并网谐波电流主要有两个来源：一部分是逆变器开关过程产生的高频电流谐波，另一部分是由电网背景谐波电压等产生的低次电流谐波。开关过程产生的高次谐波的频率远大于控制器的截止频率，只能通过输出滤波器滤除。控制策略或控制器类型的不同对此影响很小[10]，因此，一般用并网电流中的高频谐波电流的总含量来衡量输出滤波器的滤波能力。

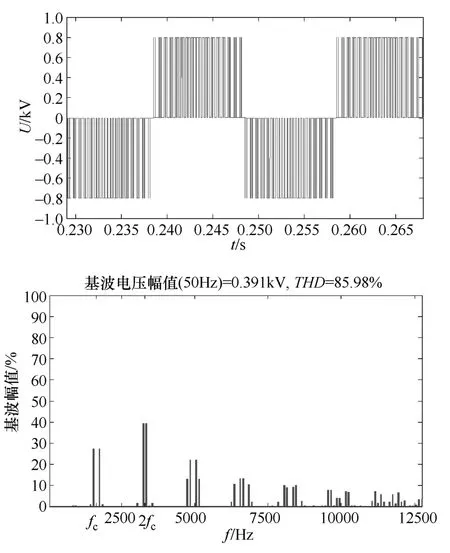
图2 三相桥式SPWM逆变器输出线电压波形及对应傅里叶分析图

为了滤除SPWM逆变器输出的高次谐波，目前主要采用LCL滤波器作为分布式电源并网逆变器的输出滤波器。LCL滤波器是由两个电感和一个电容组成的三阶结构，对于电容值为 C，逆变器侧电感值为Li，电网侧电感为 Lg的LCL滤波器，它的并网电流Ig和逆变器输出电压Ui之间的传递函数表达式为[11]

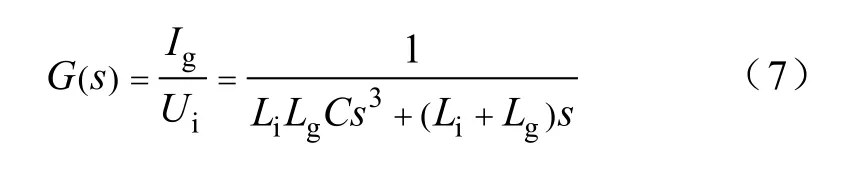
在频率足够高时，LCL滤波器以−60dB/dec衰减[11]，因此LCL滤波器具有良好的高频衰减特性，且谐波频率越高，LCL滤波器的衰减能力越强。然而逆变器开关过程中产生的高频谐波电压有很大一部分集中在fc±2fr和2fc±fr处，与其他由开关过程产生的高频谐波电压相比，这部分谐波电压的频率最低，所以LCL滤波器对于对这部分含量很大的谐波电压的滤除效果反而不好。由此可见，LCL滤波器在作为 SPWM逆变器输出滤波器时并没有最大限度地利用它的衰减特性。

为了设计一种衰减特性更适合 SPWM并网逆变器的输出滤波器结构，必须找到一种对集中在fc±2fr和 2fc±fr处的谐波电压有更好衰减效果的滤波器设计方式，陷波滤波器对于这类频率集中的谐波电压具有很好的滤除效果，故可参考陷波滤波器来设计新型输出滤波器。陷波滤波器主要依靠 LC串联谐振支路[12]进行陷波：LC串联谐振支路对于特定频率及其附近频率的电流的等效电阻很小，使这类电流都流过 LC串联谐振支路，达到陷波的目的。新型滤波器应用两段 LC串联谐振支路，分别滤除频率集中在fc和2fc附近的谐波电压。再通过逆变器和电网之间串联的滤波电感来保证新型滤波器对分散在大于2fc频段的谐波电压的滤波效果。依上述分析，得出这种新型滤波器的拓扑及其单相等效电路如图3所示。

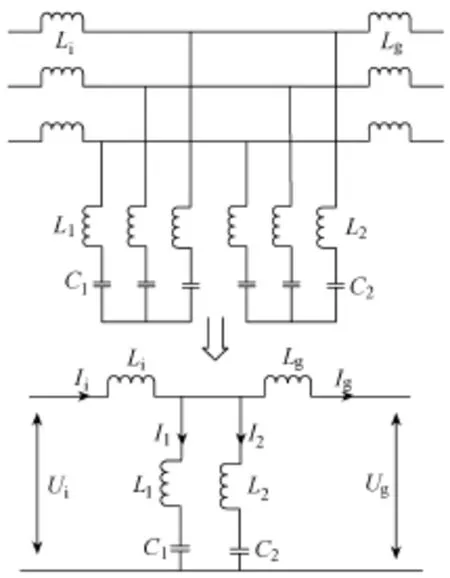
图3 双谐振滤波器拓扑结构及其单相等效电路

这种滤波器拓扑结构可以命名为双谐振滤波器。由图3可见，双谐振滤波器的串联电感分为两段：逆变器侧电感Li，网侧电感Lg。在两段电感之间有两条 LC串联谐振支路：L1C1串联谐振支路和L2C2串联谐振支路。由于双谐振滤波器主要依靠陷波特性进行滤波，所以这种滤波器结构适用于开关频率固定的分布式电源并网逆变器。

依图3中的单相等效电路，计算出并网电流Ig与逆变器输出电压Ui之间的开环传递函数表达式为

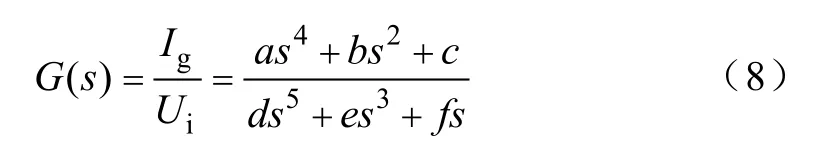
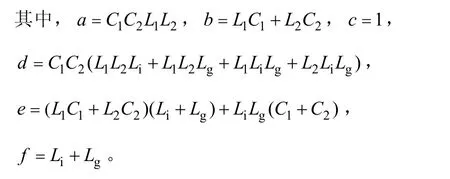
图4为依式（7）和式（8）做出的双谐振滤波器和LCL滤波器的系统开环波特图，令两种滤波器的串联电感Li与Lg取值相同，且双谐振滤波器的电容总和与LCL滤波器的电容大小相同，以便于比较。由图4可见，如果L1、L2、C1、C2的参数选择适当：①双谐振滤波器对于fc附近和2fc附近的谐波电压会有比LCL滤波器强很多的衰减作用；②双谐振滤波器在频率高于2fc时以−20dB/dec衰减，对这部分谐波的衰减能力不如LCL滤波器；③双谐振滤波器对于频率大于2fc的谐波电压的衰减能力同样很强（约与LCL滤波器在2fc附近的衰减能力相近）。因此与LCL滤波器相比，双谐振滤波器对上述三类谐波电压都具有很强的衰减能力，应用为SPWM逆变器的输出滤波器时会有更好的滤波效果。在滤波效果相似时，双谐振滤波器能大大地减少滤波器所需的总电感值。

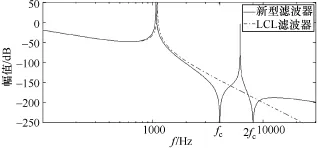
图4 双谐振滤波器与LCL滤波器的系统开环波特图

图4中双谐振滤波器的波特图存在两个负谐振峰，分别由 L1C1的串联谐振以及 L2C2的串联谐振产生的。两个负谐振峰的频率分别为

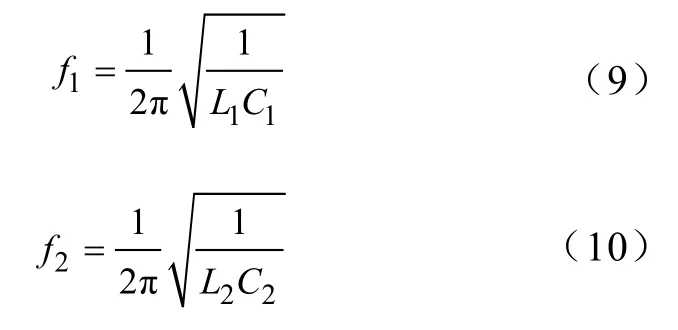
在双谐振滤波器中，令f1=fc，f2=2fc，这样两个负谐振峰就分别位于fc和2fc处。频率为fc±2fr，2fc±fr的谐波电压就能最大程度地利用这种陷波特性进行衰减。双谐振滤波器的波特图还存在两个正谐振尖峰。当L1C1支路与L2C2支路的并联回路呈容性时，该并联回路与LiLg并联的等效电感产生并联谐振，就产生了这两个正谐振尖峰。设较低的正谐振尖峰频率为fres1，较高的正谐振尖峰频率为fres2。

fres1在fr到fc之间，由于L1C1和L2C2以及fres1的取值都很小，因此在fres1处可以认为：因而在计算f时可以res1忽略L1和L2的影响。得出谐振频率fres1的估算公式如下：

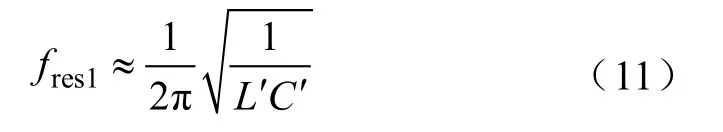
fres2在fc到 2fc之间，频率较高。由于当频率为fres2时，Li和 Lg并联的感性阻抗很大，所以与之产生并联谐振的 L1C1支路 L2C2支路并联的容性阻抗很大，估算 fres2时，可以认为该并联回路容性阻抗→∞，此时L1C1支路和L2C2支路并联谐振。则谐振频率fres2的估算公式如下：

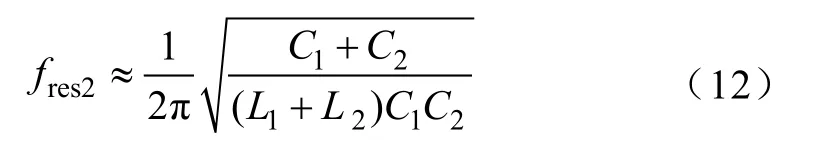
这两个正谐振尖峰和LCL滤波器中的谐振尖峰一样，不仅会导致系统中的电流谐波幅值激增，同时，会造成控制系统失稳，必须加以抑制。下文会讨论抑制这类正谐振尖峰的策略。上文分析过，SPWM逆变器输出的从fr到2fc之间的谐波电压都集中在fc和2fc附近，而其余频段的谐波电压可以忽略。因此只要令fres1与fc和fr都不是太近，fres2与fc和2fc都不是太近，在抑制谐振尖峰策略得当的情况下，两个正谐振尖峰就不会明显地放大系统的高频谐波电流。所以令

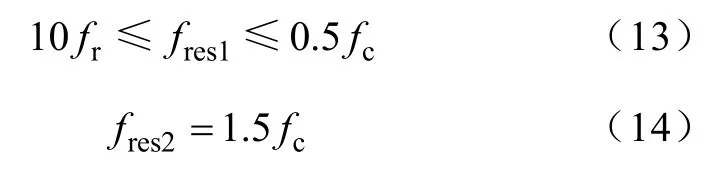
3 新型滤波器的谐振尖峰抑制

双谐振滤波器的正谐振尖峰不仅会放大谐振频率附近的谐波电流，还会在对输出电流直接进行闭环反馈控制时，造成系统失稳。因此必须对这类正谐振尖峰进行抑制。图5为双谐振滤波器主电路的等效变换框图，为简化表达，图5中将两段LC串联谐振支路的并联回路看作一个支路，用G并(s)表示该并联回路的传递函数。由第2节分析可知，双谐振滤波器产生正谐振尖峰的原因与LCL滤波器谐振尖峰产生的原因类似：当 L1C1支路 L2C2支路并联部分呈容性时（相当于LCL滤波器的电容支路），该并联部分与Li和Lg的并联电感谐振而产生的。所以双谐振滤波器的正谐振尖峰抑制也可以参考LCL滤波器抑制谐振尖峰的方法来进行。常用的抑制LCL滤波器谐振尖峰的方法有有源阻尼法和无源阻尼法[6,9,11,13-14]。由于有源阻尼法与无源阻尼法相比节省了电阻，降低了有功损耗，也不会对于高频的滤波特性产生影响[9]，是目前研究的热点问题。所以本文考虑类似有源阻尼法的方法对双谐振滤波器的正谐振尖峰进行抑制。

图5 双谐振并网滤波器主电路的等效变换框图

LCL滤波器常用的有源阻尼法为采用电容电流内环，并网电流外环的双电流内环控制的电容电流内环法[14]。这种方法不仅能很好地抑制LCL滤波器的谐振尖峰，而且属于输出电流直接控制，具有动态响应快，鲁棒性好等优点。类比这种方法，做出双谐振滤波器的有源阻尼法控制等效框图如图6所示：控制过程采用双电流内环控制，将L1C1支路和L2C2支路并联电流之和作为电流环内环，电流环内环采用比例调节，将电网侧电流作为电流环外环，电流环外环采用PI调节。这种方法可以叫做并联电流和内环法。与LCL滤波器的有源阻尼法类似，并联电流和内环法只需比正常情况下多加入一组电流传感器来测量两个 LC串联回路的电流之和，就可以实现。再根据图 6，做出并联电流和内环的开环传递函数Ig(s)/ICref(s)，即

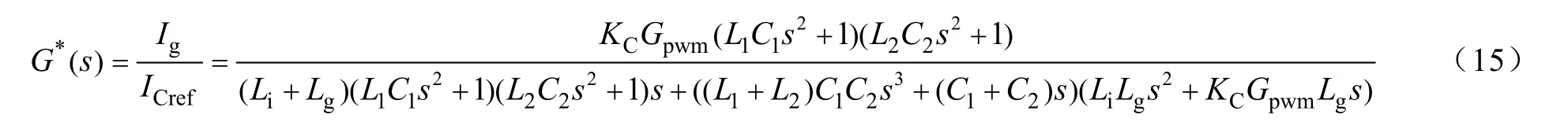
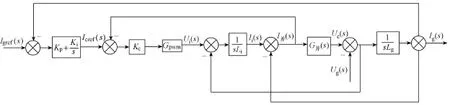
图6 并联电流和内环法的等效框图

依据式（15）作出Kc*Gpwm=0.25,0.5,2以及不存在电流环内环反馈时，电流内环的开环传递函数波特图（图7）。当存在并联电流和内环反馈时，它们的正谐振尖峰幅值都得到了不同程度的抑制，Kc取值越大，正谐振尖峰的抑制能力越强。且这种控制策略只增加了正谐振尖峰及其附近频率处的阻尼，对于其余频段的衰减特性没有影响，因而不影响高频衰减特性。与LCL滤波器的电容电流内环反馈法相似，并联电流和内环只有比例调节，会产生稳态误差。但是误差信号可以通过并网电流外环的PI调节器，实现无差跟踪。通过适当的控制参数选择，就同时解决谐振尖峰问题和并网电流的直接控制。

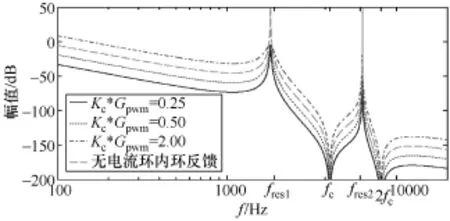
图7 加入并联电流和内环反馈后电流内环的开环传递函数波特图

4 双谐振滤波器的参数选取原则

参考 LCL滤波器的参数选取原则加以适当改进，来选取双谐振滤波器的参数，步骤如下：

1）确定LC串联谐振回路选值

首先确定总电容 C1+C2的值。两个电容 C1和C2吸收的总工频无功功率要小于额定功率的5%[11]。与滤波电感相比，滤波电容体积小，成本低。因此设计滤波器时在保证滤波效果的前提下可以适当地减少电感值，增加电容值。这里令

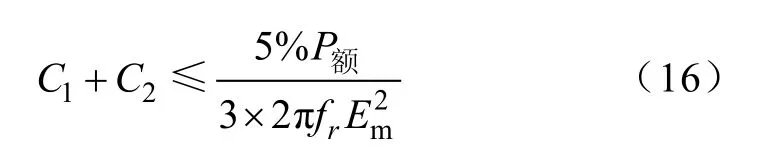
式中，P额为系统额定功率；Em为相电压有效值

根据式（9）、式（10）和式（13），令f1=fc，f2=2fc。再与式（16）联立计算出L1C1与L2C2。由于f1和f2很大，所以通常L1和L2的值很小。而且L1和L2位于LC串联谐振支路上，额定电流也很小。因此L1和L2不会对滤波器的成本和体积产生太大影响。

2）确定逆变器侧电感和网侧电感

根据对逆变器侧电流的最大纹波电流Δimax的限制，可以得出双谐振滤波器逆变器侧电感Li的要求。在SPWM调制下，Li需满足式[9]：

式中，Δimax为额定电流值的15%～40%。网侧电感Lg的取值范围参照式（11）和式（14）求得。

由前文分析可知双谐振滤波器具有良好的滤波效果。所以选取Li和Lg的值时只需在满足下限值要求的前提下留出一定的裕度。

参数选取完成后，通过计算额定情况下，并网电流中高频谐波电流畸变 Itotal来衡量滤波器的滤波性能。式（18）通过估算fc附近，2fc附近和剩余所有频段的三类谐波电压造成的谐波电流畸变，得出高频谐波电流总畸变Itotal的估算公式：

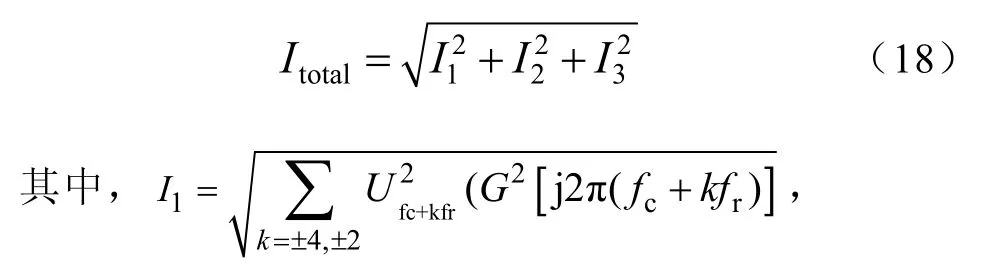
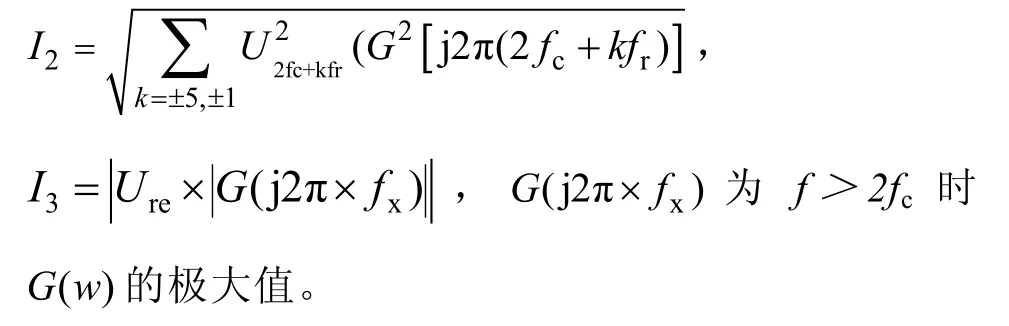
式（18）中计算I3时采用的是G( w)在频率大于2fc时的最大值，故I3是估算值，导致计算出的Itotal比实际值偏大。

最后，还需要验证各次高频谐波电流满足IEEE Std.519中的规定，验证式为

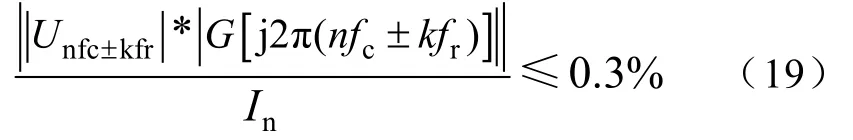
5 仿真验证

为了验证双谐振滤波器的滤波效果，在PSCAD仿真平台下搭建额定功率为20kW的三相并网逆变器，采用SPWM调制，令开关频率fc=4050Hz，直流源电压 Ud=800V，电网的线电压为 U=380V，网侧频率fr=50Hz。分别用双谐振滤波器和LCL滤波器作为这种三相并网逆变器的输出滤波器。双谐振滤波器依照第4部分的参数选取原则取值，再设计一个高频谐波电流总畸变 Itotal与双谐振滤波器相近的LCL滤波器，滤波器参数取值见表1。为便于比较两种滤波器的滤波效果，令LCL滤波器的Li=Lg，这时它的高频滤波性能最好[15]。

表1 滤波器各元件参数取值

令逆变器工作在额定情况下，LCL滤波器的电流环采用电容电流内环法，双谐振滤波器的电流环采用并联电流和内环法。在保证控制稳定的基础上，分别比较二者对于高频谐波的滤波效果。二者的输出相电流波形和傅里叶分析图如图8和图9所示。综合图8、图9以及表1分析如下。

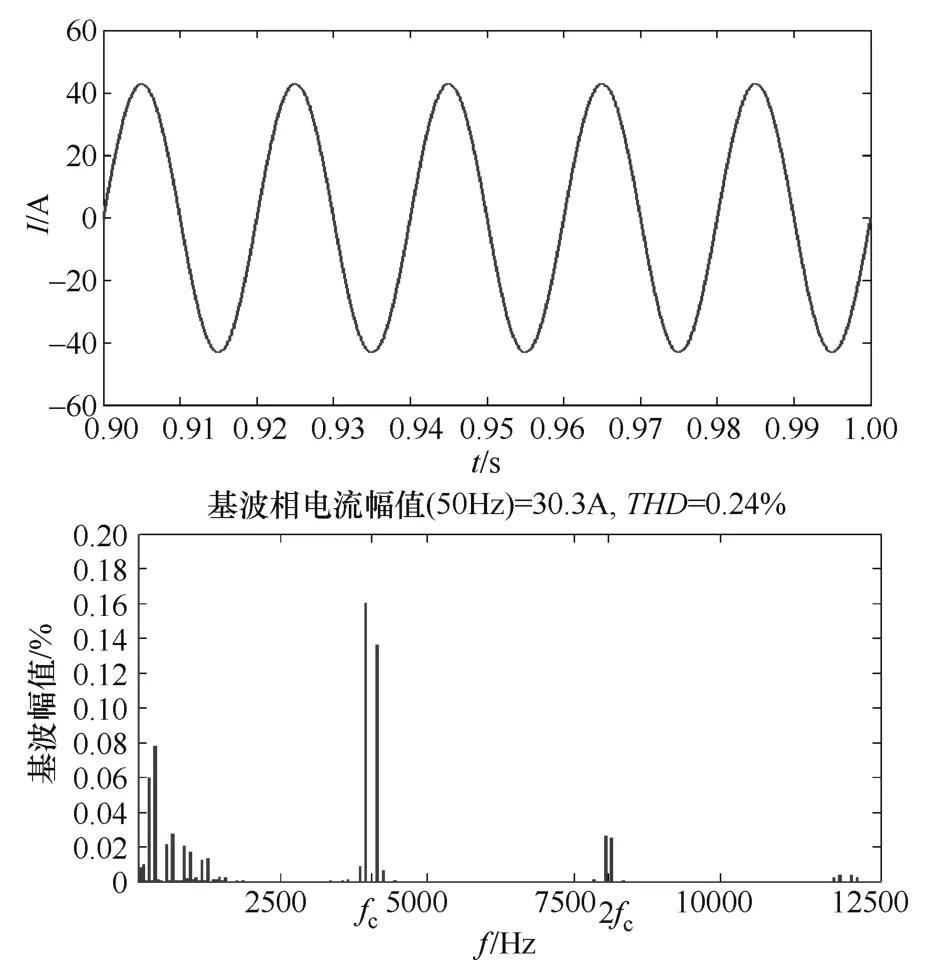
图8 LCL逆变器输出的相电流波形图及傅里叶分析图

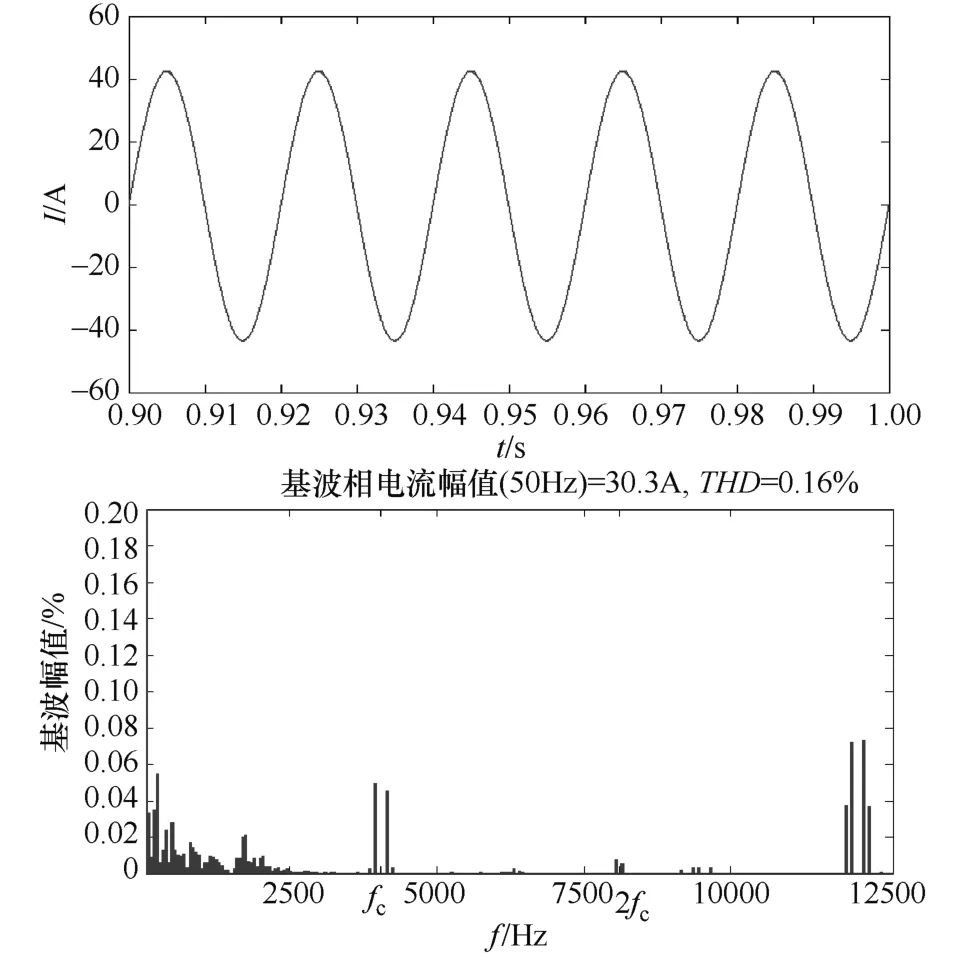
图9 双谐振滤波逆变器输出的相电流波形图及傅里叶分析图

1）LCL滤波器需要4.2mH的总电感，而双谐振滤波器所需的总电感仅为2.2mH（忽略LC谐振支路的电感值），减少了近一倍的总电感值，以电感的额定电流均选为30A为例，总的电感体积能减少大约30%，同时大大降低了滤波器的成本以及滤波器的体积。

2）双谐振滤波器两个正谐振尖峰频率附近的谐波电流含量均很小，两个正谐振尖峰附近含量最高的谐波电流只有约0.03%In，说明并联电流和内环法很好地抑制了两个正谐振尖峰。

3）双谐振滤波器很好地抑制了 fc附近和 2fc附近的谐波，对于其余频段的谐波也有不错的抑制效果。输出相电流 THD=0.161%，含量最高的高频段谐波电流为0.073%In，对于LCL滤波器，输出相电流 THD=0.237%，含量最高的高频段谐波电流为0.159%In。说明在仿真设置的参数下，双谐振滤波器的滤波效果要好于LCL滤波器。

6 结论

本文通过分析采用 SPWM调制的并网逆变器的输出谐波电压分布，指出了目前常用的LCL滤波器在衰减这些谐波电压时的缺陷，提出了一种新型滤波器——双谐振滤波器：

1）从硬件结构上看，双谐振滤波器是将 LCL滤波器的电容回路替换为两段并联的 LC串联谐振支路，利用这两段支路分别滤除在fc附近和2fc附近的含量很大的谐波电压，通过逆变器侧电感和网侧电感的共同作用来保证其余分散在 2fc以上的高频谐波电压的衰减能力，结构增加了一定的复杂性。

2）从成本和效果上看，双谐振滤波器和传统的LCL滤波器相比，在使用相同大小的电容的情况下，双谐振滤波器总电感的需求减少近一倍，且滤波效果更好，极大地降低了滤波器的成本和体积。

3）从控制方式上看，双谐振滤波器产生正谐振尖峰的原因与 LCL滤波器谐振尖峰产生的原因类似：当 L1C1支路 L2C2支路并联部分呈容性时（相当于LCL滤波器的电容支路），该并联部分与Li和Lg的并联电感谐振而产生的。所以双谐振滤波器的正谐振尖峰抑制可以参考LCL滤波器抑制谐振尖峰的方法来进行。有源阻尼法是抑制LCL滤波器谐振尖峰的常用方法，即采用电容电流内环，并网电流外环的双电流内环控制的电容电流内环法。类比这种方法，双谐振滤波器控制过程可采用并联电流和内环法，其实现只需增加一组电流传感器来测量两个LC串联回路的电流之和。

因此，双谐振滤波器相比LCL滤波器，在增加有限的硬件结构复杂度的前提下，控制方法上几乎没有变化，但是成本大大降低，滤波效果显著提高，因而具有很高的工程实用价值。

[1]陈维,沈辉,邓幼俊,等.光伏发电系统中逆变器技术应用及展望[J].电力电子技术,2006,40(4):130-133.

[2]王长贵,王斯成.太阳能光伏发电实用技术[M].北京:北京化学工业出版社,2009.

[3]IEEE Working Group.IEEE Recommended Practices and Requirements for Harmonic Control in Electric Power System[S].1992.

[4]刘飞,查晓明,段善旭.三相并网逆变器 LCL滤波器的参数设计与研究[J].电工技术学报,2010,25(3):110-116.

[5]Lang Y Q,Xu D G,Hadianamrei S R,et al.A novel design method of LCL type utility interface for three-phase voltage source rectifier[C]//2005 IEEE 36th Power Electronic Specialists Conference (PESC),Vols 1-3,2005:313-317.

[6]沈国桥,徐德鸿.LCL滤波并网逆变器的分裂电容法电流控制[J].中国电机工程学报,2008,28(18):36-41.

[7]曹立威,吴胜华,张承胜,等.SPWM谐波分析的一般方法[J].电力电子技术,2002,36(4):62-65.

[8]莫叶.复变函数论[M].济南:山东科学技术出版社,1980.

[9]张崇巍,张兴.PWM整流器及其控制[M].北京:机械工业出版社,2003.

[10]Cobreces S,Bueno E,Rodriguez F J,et al.Influence analysis of the effects of an inductive-resistive weak grid over L and LCL filter current hysteresis controllers[C]//2007 EUROPEAN CONFERENCE ON POWER ELECTRONICS AND APPLICATIONS,VOLS 1-10,2007:518-527.

[11]刘飞,段善旭,查晓明.基于 LCL滤波器的并网逆变器双环控制设计[J].中国电机工程学报,2009,29(S1):234-240.

[12]森荣二.LC滤波器设计与制作[M].北京:科学出版社,2006.

[13]Malinowski M,Bemet S.A simple voltage sensorless active damping scheme for three-phase PWM converters with an LCL filter[J].IEEE Transactions on Industrial Electronics,2008,55(4):1876-1880.

[14]鲍陈磊,阮新波,王学华,等.基于PI调节器和电容电流反馈有源阻尼的LCL型并网逆变器闭环参数设计[J].中国电机工程学报,2012,32(25):133-142.

[15]魏星.基于LCL滤波器的三相并网逆变器的研究[D].南京:南京航空航天大学,2011.

Design and Implementation of a Novel Filter in Grid-connected Inverter

Zhang Weiya1Wang Ziyu2
(1.Nanjing Electrical Power Company,Nanjing 210019;2.Xuzhou Electrical Power Company,Xuzhou,Jiangsu 221000)

In order to solve the high frequency harmonic pollution problem caused by the grid-connected inverter,the harmonic voltage distribution under the switch process of grid-connected inverter are calculated and analyzed.On the base of which a novel double resonance filter for filtering the switching harmonic voltage is proposed.Compared with the existing LCL filter,the new one has better high frequency harmonic attenuation characteristics with less total inductance,which reduces the cost and volume of the filter.The parameter design principle and implementation method are introduced as well.Finally,the effectiveness and feasibility are verified by simulation results with PSCAD.

grid-connected inverter;filter design;SPWM harmonic analysis;active damping method

张玮亚（1988-），男，博士，河南新乡人，主要从事电力系统保护和控制、分布式电源和储能技术的研究工作。