基于ARIMA模型的澳门本地生产总值未来走势预测

澳门科技大学商学院 莫文权 李坤达 王尚

基于ARIMA模型的澳门本地生产总值未来走势预测

澳门科技大学商学院 莫文权 李坤达 王尚

澳门赌收持续下跌已经有一年多了，经济前景的不明朗，对各行业的负面影响开始浮现。在种种不利因素的影响下，澳门政府需及时调整相对应的宏观经济策略，制定正确的经济发展策略，有效地预测并分析澳门未来GDP走势的整体情况。本文基于时间序列的分析方法对澳门本地生产值总值(GDP)进行建模分析，选择最佳的ARIMA模型对资料进行拟合。通过一系列的实证分析，结果表明ARIMA模型能够有效地预测澳门GDP的走势状况。

ARIMA模型 时间序列分析 澳门本地生产总值

1 模型的应用

1.1 ARIMA(p,d,q)(P,D,Q)S模型介绍

对于包含趋势性的原序列，可用ARIMA(p,d,q)模型进行拟合，称之为自回归求积移动平均模型。若序列同时包含趋势性及季节性，则可使用ARIMA(p,d,q)(P,D,Q)S模型进行拟合，称之为季节自回归求积移动平均模型。该回归模型和ARIMA(p,d,q)模型类似，两者的主要区别是对于ARIMA(p,d,q)(P,D,Q)S模型我们不但需要对原始的时间序列做d阶差分，而且还需要做D阶的季节性差分，以此来消除原始序列存在的季节性。由于澳门本地生产总值季度资料同时存在趋势性及季节性，所以，本文将采用ARIMA(p,d,q)(P,D,Q)S模型对原始时间序列进行拟合，该模型的数学运算式如下为随机项。

1.2 预测及预测评价

采用历史类比的方法来评价模型的有效性。通过使用部分历史资料建立拟合模型，再用模型对剩下的另一部分的历史资料进行预测，通过比较分析实际的历史资料和通过模型计算出的预测资料来评价模型在预测水准上的有效性。具体使用如下的指标检验模型预测的有效性。

第一，平均相对误差绝对值(MAPE)：

第二，Theil不相等系数：

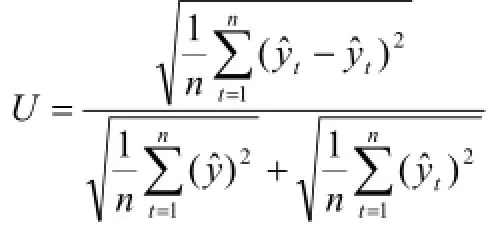
Theil不等系数可分解为偏倚比例(Basic Proportion)、方差比例(Variance Proportion)和协方差比例(Covariance Proportion)三部分

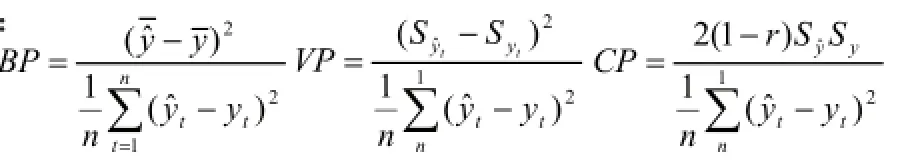
如果预测模型是有效精准的，各项指标则满足以下情况：平均相对误差的绝对值较小；U值接近于零；偏倚比例和方差比例较小；协方差比例较大。

2 实证分析

本文的资料来源于澳门统计暨普查局公布的澳门本地生产总值的季度资料，时间跨度为2001第一季度年至2015年第四季度。本文将澳门本地生产总值的季度数据简记为GDP序列，以百万元为单位。图1是2001年第一季度至2015年第四季度的GDP本地生产总值折线图，本地生产总值存在明显的增长趋势及包含周期为四个季度的季节性变动。同时由原始GDP序列的相关图可得，自相关系数直至滞后期数为k=15时依然显著，表现拖尾；偏自相关系数则在滞后期数为k=1时截尾，说明原始GDP序列是非平稳的时间序列。

图1 澳门季度本地GDP折线图

为了消除原始GDP序列存在的趋势性，并减少数据的波动，笔者对原始序列做自然对数变化处理，形成新的对数序列名lngdp，再进行一阶差分，差分后序列名为dlgdp。差分后序列的增长趋势基本被消除，但当滞后阶数k=4时，样本的自相关系数和偏自相关系数均显著不为零，表明原始序列存在一定的季节性。需要对序列dlgdp做季节性差分，得到新序列名sdlgdp。

经过两次差分后，原始GDP样本序列的自相关系数和偏自相关系数均变为较小，并在零值附近上下波动，大部分值落在置信限内。但在滞后期k=4时，自相关系数和偏自相关系数依然较大且均落在置信限外，表明经过一阶季节差分后，序列仍然存在季节性。经过继续试验，本文对序列进行二阶的季节差分，发现二阶的季节差分未能进一步地消除序列依然存在的季节性，所以本文做一阶的季节差分即可。

2.1 序列零均值检验及平稳性检验

建立ARIMA模型的重要前提是序列sdlngdp的均值为零，所以，我们需要对序列进行零均值检验。计算结果显示序列的均值落在的范围内，说明序列的均值为零，序列通过零均值检验。接着使用ADF的检验方法对序列进行单位根检验，检验的结果显示，在95%的置信水平下计算的统计量为-3.495，大于-8.1489的ADF临界值，说明序列经过差分处理后已成为平稳的时间序列，可建立ARIMA模型。

2.2 ARIMA模型的识别

原始GDP序列即存在增长趋势同时也存在季节性，因此本文选择建立ARIMA(p,d,q)(P,D,Q)S模型，称为季节自回归移动平均模型。由上文可知原始序列经过一阶差分后，序列存在的增长趋势已被消除；另外经过一阶的季节性差分，序列的季节性问题也得到了改善，故确定季节差分的阶数为D=1。序列sdlngdp的自相关函数和偏自相关函数均是截尾，且均在滞后期为k=2时出现截尾，故设定自回归的滞后阶数为p=2或者p=3比较合适；同时设定移动平均的滞后阶数为q=2。又因为原始序列存在季节性问题，且季节波动的周期为四个季度，所以ARIMA(p,d,q)(P,D,Q)S模型的季节自回归和季节移动平均的滞后阶数为P=Q=1。为了进一步得到拟合度及预测精准度较高的回归模型，本文分别建立ARIMA(2,1,2)(1,1,1)4模型和ARIMA(3,1,2)(1,1,1)4模型，并根据两者比较的检验结果，选择建立滞后阶数最佳的ARIMA(p,d,q)(P,D,Q)S模型。

2.3 模型的建立及检验

经过上述分析比较，本文分别建立ARIMA(2,1,2)(1,1,1)4和ARIMA(3,1,2)(1,1,1)4模型，并比较模型回归的检验结果，如表1所示。

表1 两个ARIMA模型的检验结果

根据回归结果显示，两模型各滞后多项式的倒数根均落在单位圆以内，说明ARIMA(2,1,2)(1,1,1)4和ARIMA(3,1,2)(1,1,1)4模型的回归过程是平稳、可逆的，两模型设定均合理。进而通过表4比较两ARIMA模型的回归检验结果，表1显示ARIMA(3,1,2)(1,1,1)4模型的SCI值和SC值均最小的,残差平方和也为最小；同时注意到ARIMA(3,1,2)(1,1,1)4模型修正后的拟合度也比ARIMA(2,1,2) (1,1,1)4模型的大，相比之下ARIMA(3,1,2)(1,1,1)4模型各方面均最优，所以选择建立最佳的ARIMA(3,1,2)(1,1,1)4模型，其回归结果如表2所示。

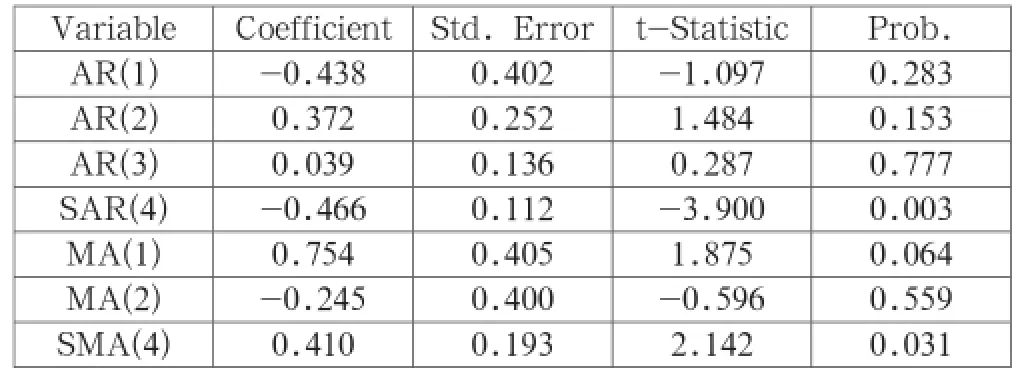
表2 ARIMA(3,1,2)(1,1,1)4模型回归结果

回归模型的表达式如下：

2.4 模型预测

利用拟合精度较高的ARIMA(3,1,2)(1,1,1)4模型，首先对2015年第一季度到第四季度的澳门本地GDP进行预测，然后和2015年实际的季度GDP进行比较得出误差百分比。紧接着再对澳门2016年四个季度的本地生产总值进行有效预测。

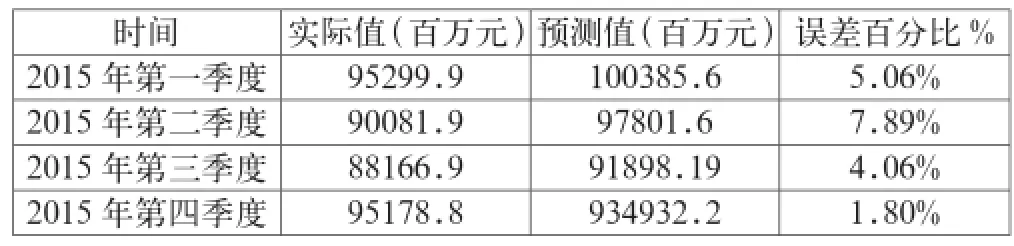
表3 ARIMA(3,1,2)(1,1,1)42015年第一季度到第四季度GDP的实际值和预测值比较

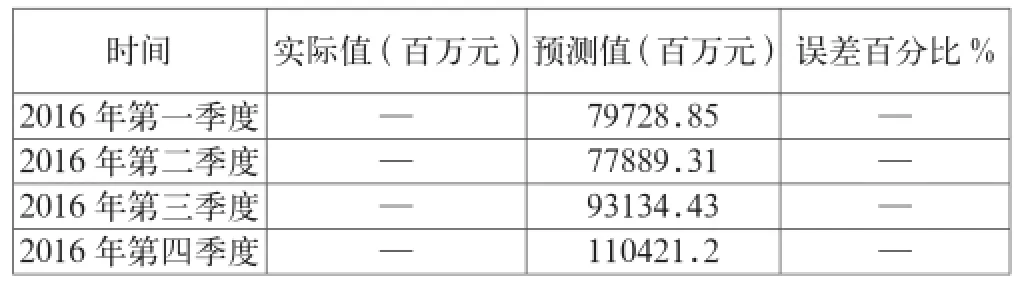
表4 ARIMA(3,1,2)(1,1,1)42016年第一季度到第四季度GDP的预测值

由表3可得，在ARIMI(3,1,2)(1,1,1)4模型计算出的2015年第一季度到第四季度澳门本地GDP的预测值和实际值的比较中，误差百分比均较小，均控制在8%以内。平均相对误差(MAPE)约为4.97%，Theil不等系数值为0.0286，接近于零。模型的偏倚比例、方差比例和协方差比例分别为0.5394、0.00229、0.4582，这都说明了模型对未来澳门本地生产总值的预测值符合实际的情况，模型能够进行可靠的预测。进而由表4可得，该模型预测2016年第一季度到第四季度的本地生产总值，这些预测值在一定程度上代表了澳门本地生产总值的未来走势，为澳门政府根据预测的经济走势状况来制定相对应的货币及财政决策提供一定的借鉴意义。进一步讨论，将2016年四个季度的预测值相加得出2016年度本地GDP的总值约为36117379万元，与2015年实际的年度GDP总值36872750万元相比，澳门2016年的经济总量将会下降约2.048%，大约为750亿元左右。

3 结语

澳门本地生产总值季度资料GDP序列为非平稳的时间序列，是一组依赖于时间t的随机变数,在消除序列的异方差性、趋势性及季节性后，通过建模回归分析比较后，建立最佳的 ARIMI(3,1,2) (1,1,1)4模型。经过实证分析结果显示，该模型的相对误差百分比在1.80%～7.90%之间，预测精度较高，可用于澳门本地生产总值的短期预测。根据预测的结果显示，2016年澳门年度本地生产总值将约为361173.79百万元，同比下降2.048%，预测今年澳门的经济状况将会继续下滑。

[1] 柴攀峰．ARIMA模型预测浙中核心城市固定资产投资增长率[J]．科技与管理，2014(02)．

[2] 洪丰．基于ARIMA模型预测中国未来能源消耗[J]．南昌工程学院学报，2011(4)．

[3] 孙亚星．我国货币供应量因素分解模型与ARIMA模型预测[D]．中南大学，2009．

F127

A

2096-0298(2016)08(a)-099-02