机器人避障问题数学模型研究

王 瑞 孙 晰

1.辽源职业技术学院，吉林 辽源 136201；2.洛阳市第一中学，河南 洛阳 471000



机器人避障问题数学模型研究

王 瑞1*孙 晰2

1.辽源职业技术学院，吉林 辽源 136201；2.洛阳市第一中学，河南 洛阳 471000

机器人是一种能够在正常工作环境中自由移动、并顺利完成预定任务的智能系统。机器人的避障问题是移动机器人控制领域的研究热点。模型对机器人避障问题，分不考虑转弯和考虑转弯两种情况的路径，采用传统算法、智能算法进行了讨论。

最短路径；类比法；距离；勾股定理

在一个800×800的平面场景图，原点O处有一个机器人，它只能在该平面场景范围内活动。图中有12个不同形状的区域是机器人不能与之发生碰撞的障碍物。在图1的平面场景中，障碍物外指定一点为机器人要到达的目标点(要求目标点与障碍物的距离至少超过10个单位)。规定机器人的行走路径由直线段和圆弧组成，其中圆弧是机器人转弯路径。

一、问题分析

为了方便解决问题，将机器人看成点。先不考虑与障碍物的距离，连接点O与障碍物的顶点、障碍物顶点与顶点、顶点与目标点的直线为机器人的行走路径，比较这样的路径中最短者。再将各障碍物向外平行扩展10个长度单位，借鉴上述最短路径，从而画出满足条件的最短路径并求其长度。

二、模型的建立与求解

先不考虑转弯情形,给出O→A→B→C→O的线路图，以下均见图1。

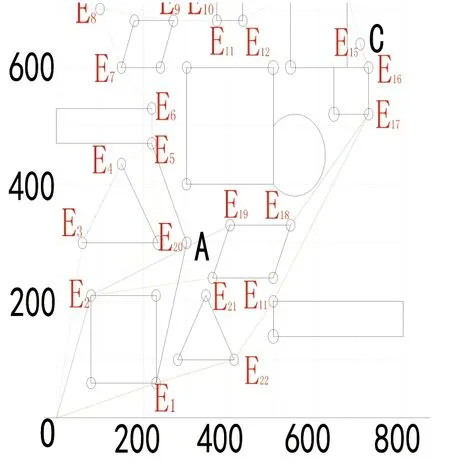
图1 O→A→B→C→O可行路径图

因为机器人所走的弧长比线段长少很多，所以可将机器人看成点。已知各障碍物顶点坐标，用C语言编程可得各路径的总路程，最后得出：

O→A的最短路径为O→E2→A，距离为462.417。

O→B的最短路径为O→E2→E4→E7→E8→E9→B，路程为845.42。

O→C的最短路径为O→E1→E21→E19→E15→E14，路程为1069.68。

A→B的最短路线为A→E5→E6→E7→B，距离为458.21。

B→C的最短路线为下表路径一，距离为683.35。

上述结论未考虑与障碍物的距离.下面将距离考虑在内,给出机器人绕障碍物的最短路径方案及路程。机器人所走的路径，包括从O→C及再回到终点的路径，可推广出以下通式。

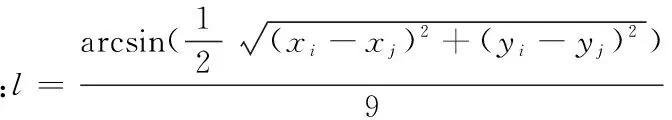
通过求不考虑圆弧与考虑圆弧的路程看出，有圆弧的路径可使机器人避开障碍，且为最短路径。

O→A含弧的最短距离为466.51。O→B的含弧最短距离为832.87。

O→C的最短距离为1055.26。A→B的含弧最短距离为458.21。

B→C的最短距离为683.35。O→A→B→C→O的最短距离=2663.33。

若要求出从O到A得最短时间路径，先求出OA的最短路径为O,M1,M2,A,以此路径为基础与其他路径进行比较，找到最短时间路径，如图2所示:

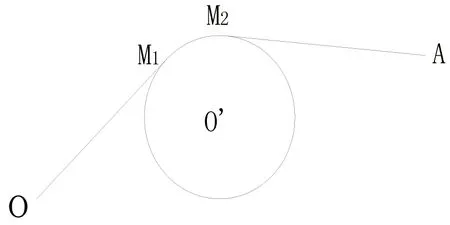
图2 最短时间线路图

综上，机器人的应用领域正不断扩大，种类日趋增多，性能不断提高，并逐步向智能化方向发展，追求目标是融入人类的生活，和人类一起协同工作，从事一些人类无法从事的工作，以更大的灵活性给人类社会带来更多的价值。

[1]谢云荪,张志让.数学实验.北京：科学出版社，1999.

[2]吴建国.数学建模案例精编.北京：中国水利水电出版社，2005.

TP242;O

A