运用比较法让初中数学课化繁为简

王文娟

河北省冀州市冀州镇中学



运用比较法让初中数学课化繁为简

王文娟

河北省冀州市冀州镇中学

数学问题浩如烟海，面对一个个数学问题如何着手求解?有些学生做了大量的题目，但考试遇到新题型或只是稍稍变换一下，就不知所措，原因是在平时的学习中，缺乏掌握数学思考方法。掌握一种新的思考方法要比学会解几道具体习题更为重要，这些解题方法和技巧是进一步学习数学不可缺少的工具，数学方法的学习，在数学学习中起到事半功倍的效果。比较法就是找出一事物区别其他事物的特点，通过对比可以找出差异，有助于进一步加深对新知识的理解，揭示新知识的本质。

在数学教学中恰当地运用比较法，不但能突出教学的重点，简化某些教学环节，而且有利学生理解和掌握概念，提高解题能力和发展思维能力。下面我就谈谈比较法在初中数学教学中的应用。

一、用比较法教学，加深对概念的理解

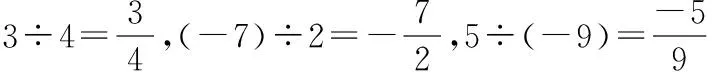
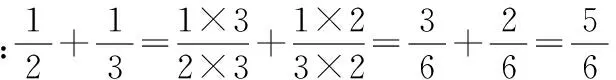
第三，分式的四则运算顺序也可以类比分数进行，先做括号内的运算，然后再进行乘除运算，最后进行加减运算，这个顺序和步骤正是分式四则混合运算的顺序和步骤。概括地说是：“先乘除，后加减、括号内先进行”。

教学一元二次方程定义时，要求学生与一元一次方程定义比较。

有些比较，需要老师适当的引导，如在几何教学中把相似三角形与全等三角形，它们的相同点是都具备对应角相等，对应边成比例，但如果对应边比例等于1，则相似即相等。又如有理式与分式比较，有理式包括整式和分式。分式是有理式的一部分，解方程与解不等式的解法大同小异。实践证明，通过比较法能把一些易混淆的概念清楚地区分出来，使学生掌握和运用数学概念解决问题方面，起到事半功倍的效果。

二、用比较法教学，加深对新知识理解

教材中有较多的内容，在讲授新知识的同时可以联系旧知识并进行比较，这无论对学生掌握知识还是培养思维能力都是十分有效的。例如，教一元一次不等式解法时先复习一元一次方程的解法，然后说明一元一次不等式与一元一次方程在解法上基本相同，不同点是不等式两边同时乘以或除以同一个负数，不等号方向改变。又如，解含有字母系数的一元一次方程，分式方程都可以与解一元一次方程相比较，三角形相似判定定理与全等三角形判定定理比较，等等。初中数学的每个新知识点几乎都可以找到一个与之联系紧密的旧知识比较，采用比较法教学，不仅可以巩固原有的知识，而且使新知识在比较中纳入学生已掌握的知识结构中，把旧知识可能引起的负向迁移转化为正向迁移。这样，既顺利完成新知识教学，又有利帮助学生建立科学的认知结构。

三、用比较法教学，提高解题能力

初中教学教材内容丰富，展现在学生面前的是千变万化的数学题。学生在教师正确指导下，运用学过的知识，技巧和方法，通过认真比较，不但能掌握解题方法，而且能提高解题能力。例如，上因式分解复习课时，由于因式分解内容多、方法多，给出一个多项式学生往往不懂如何解答。这样可以引导学生通过比较多项式的项选适当方法，如：(1)有两项考虑用平方差方式；(2)有三项考虑用完全平方公式或(x+p)(x+q)的形式。通过比较复习，不仅使学生掌握因式分解的方法，还能使学生在较少时间内复习较多内容，提高复习效率和解题综合能力。

此外，开立方与开平方，中心对称与轴对称；扇形面积公式与三角形面积公式等等，都可以通过类比和对比进行教学，这种数学方法的教学，学生在学习过程中能较轻松地接受新知识。在教学中运用比较法常常能把抽象问题变具体，把复杂问题变简单，化难为易，使学生较易找出解题方法。在实践中也证明，这种比较法的数学方法，学生掌握的知识扎实，理解也较好。当然，比较法只能用来帮助我们建立猜想，作为研究问题的线索。

总之，通过对比学习训练,学生大脑中原来的思维定势被打破,并很快升华到一个新的水平,在新的高度上重新形成一个新的思维定势。静态的思维方式被转化动态的思维方式,有利于培养学生的动态发散性思维能力。学会学习新知识、新方法学习方法,形成从容跨入新的知识境界的能力,进而造就学生良好的数学素质和学习探讨能力。