社会媒体环境下基于EMD-DSVR的股票市场预测方法研究

梁 坤,张理政

（1.合肥工业大学 管理学院，合肥 230009，2.安徽建筑大学 管理学院，合肥 230022）

社会媒体环境下基于EMD-DSVR的股票市场预测方法研究

梁 坤1,张理政2

（1.合肥工业大学 管理学院，合肥 230009，2.安徽建筑大学 管理学院，合肥 230022）

现有的利用社会媒体预测股票市场的研究未能考虑股指时间序列所具有的多尺度特征。为了解决这一问题，运用EMD分解法、混沌分析理论和支持向量回归机，提出一种EMD-DSVR股票市场预测方法。首先分析股指时间序列多尺度与社会媒体变量序列多尺度间的内在联系，运用EMD分解法将社会媒体变量序列分解成不同尺度的基本模态分量；然后运用混沌分析理论和支持向量回归机对各模态分量进行建模和预测；最后利用社会媒体变量序列的各模态分量对股票市场进行预测。运用所提出的EMD-DSVR模型，对上证指数和深成指数的日收盘值进行预测，实验结果表明，所提出的方法能有效提高对股指时间序列的预测精度。

经验模态分解；股票收益；混沌理论；支持向量回归

0　引言

股票市场是金融市场的重要组成部分，也是国家经济运行状况的晴雨表。合理分析并预测股票市场不仅能够引导股民进行正确投资，还可以为政府提供股票市场宏观调控的理论依据，进而保障经济平稳健康发展。

传统的股票市场分析与预测主要有基本面法和技术分析法[1]。随着论坛、博客和内容社区等社会媒体的快速发展与广泛应用，基于社会媒体的股票市场预测逐渐成为新的研究热点[2]。已有研究表明，社会媒体中的用户生成内容能够显著影响投资者的投资决策行为，进而造成股票价格、交易量和收益率等的变化[3-6]。Frank的研究指出，社会媒体的信息数量与股票价格波动成正比，与股票收益率成反比[3]。Bollen利用文本处理技术分析Twitter上的公众情绪，并指出公众情绪的变化能显著影响道琼斯工业平均指数[4]。Hsinchun Chen的研究表明，通过分析投资者论坛上的讨论话题和干系人组成，能够更加细粒度的反映股票的市场行为[5]。 Jiang研究了突发事件不同阶段雅虎金融论坛上的发帖数量和情感倾向与股票收益率间的关系，研究结论表明，社会媒体变量与股票收益率间的关系在突发事件不同阶段是不同的[6]。上述研究主要从社会媒体内容方面对股票市场预测展开研究，也有学者从社会网络分析视角研究社会媒体对股票市场的影响。例如，Zhang指出，Twitter上有关股票主题的被转发次数与标准普尔500指数呈显著的正相关关系[7]。

然而，现有的关于利用社会媒体预测股票市场的研究很少考虑股指时间序列所具有的多尺度特征[8]。不同时间尺度的交易者对股票市场和社会媒体关注的时间尺度是不同的：短期投资者一般关注短时间内的社会媒体股票信息；而长期投资者一般综合分析较长时间内的社会媒体股票信息，更关注股票收益的长期走势[9]。为了综合考虑不同类型交易者对股票市场产生的整体影响，并提高社会媒体对股票市场的预测性能，需要相应的对社会媒体变量序列进行多尺度分析。

小波分析在时域和频域均具有良好的分析能力，因此，基于小波分析的股指时间序列预测逐渐受到学者们的青睐[10-15]。然而，小波分析具有以下两点不足[16]：第一，小波分解不能根据信号本身特性进行自适应分析，通常会产生很多虚假的谐波；第二，小波分解需预先人为设定时间尺度，导致小波分解不能客观反映信号中所包含的各尺度上的信息。经验模态分解（Empirical mode decomposition, EMD）能够基于信号局部特征，将原始序列中不同尺度的波动或趋势逐级分解开来，产生一系列模态函数（Intrinsic mode function, IMF），其中每个模态函数均可以反映原始序列在不同尺度上的波动特征。由于EMD方法可以更准确的反映原始序列的物理特性，因此在处理非线性、非平稳时间序列时，EMD较之小波分解更加有效[17]。

本文将EMD方法与支持向量回归（Support vector regression, SVR）相结合，对中国股票市场进行预测。首先利用EMD方法将社会媒体变量序列分解成若干个IMF；然后针对每个IMF进行混沌序列的支持向量回归建模；最后，利用社会媒体变量序列的各IMF和股指时间序列的前期值对股票市场进行预测。由于EMD方法能将复杂的社会媒体变量序列分解成若干个彼此间影响甚微的基本模态分量，从而使得支持向量回归机能更加准确的把握社会媒体变量序列的多尺度特征，而且还能综合考虑不同类型交易者对股票市场产生的整体影响，从而最终提高模型的预测精度。

1　基于EMD的双重支持向量回归预测模型

为了提高社会媒体对股票市场的预测性能，考察社会媒体变量序列的各尺度模态分量对交易者产生的综合影响，提出一个基于EMD的双重支持向量回归预测模型（Empirical mode decomposition and double support vector regression, EMD-DSVR），该模型的预测流程分为三个阶段，如图1所示。首先利用EMD分解法将社会媒体变量序列SM(t)分解成不同时间尺度的模态分量和长期趋势项；然后通过计算各模态分量的嵌入维数和延迟时间，建立各模态分量的混沌模型CMi，并利用前层支持向量回归机对各模态分量进行预测，对于长期趋势项的预测则采用拟合函数法；最后将股指时间序列的前期值和上一阶段中各序列的预测值Pi一同输入后层支持向量回归机中，预测股指时间序列的下一个数据点。

图1　EMD-SVR预测模型整体框架

设SM(t)和S(t)分别为t时刻的社会媒体变量序列和股指时间序列，sm(t)和s(t)分别为SM(t)和S(t)在t时刻的取值，则EMD-DSVR预测方法的数学模型和具体实现步骤如下：

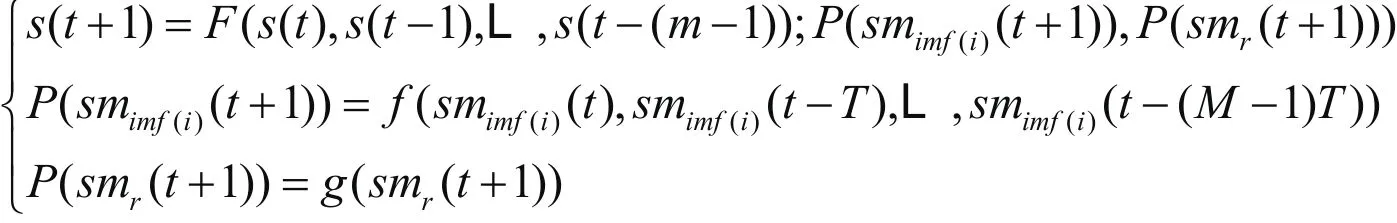
步骤1：利用EMD方法将社会媒体变量序列SM(t)分解为有限个基本模态分量SMimf(i)(t) (i=1，…，n)和长期趋势项SMr(t)。

步骤2：根据混沌分析理论，对SMimf(i)(t)，(i=1，…，n)进行相空间重构，通过计算社会媒体变量序列各模态分量的延迟时间和嵌入维数来对各模态分量进行插值，并确定前层支持向量机的结构参数。其中延迟时间可由互信息法来确定，将imf(i)的互信息函数第一次达到局部极小值时的t作为最佳延迟时间T[18]；嵌入维数的选择使用假近邻法，即累积假近邻点占总点数的比例小于一定阈值所对应的维数m为嵌入维数M[19]。

步骤3：将插值后的SMimf(i)(t)，(i=1，…，n)输入前层支持向量回归机，其中输入变量即为步骤2中按照延迟时间和嵌入维数确定的各项插值，输入节点数即为嵌入维数M，得出SMimf(i)(t)在t+1时刻的预测值P(smimf(i)(t+1))。对长期趋势项SMr(t)采用线性拟合的方法进行预测，得到SMr(t)在t+1时刻的预测值P(smr(t+1))。

步骤4：对社会媒体变量序列的各模态分量和长期趋势项预测完成后，将得到的预测结果输入后层支持向量回归机。此外，由于金融时间序列具有自相关性[20]，将股指时间序列的前期值作为控制变量一同纳入预测模型，并输入后层支持向量回归机。

2　实验研究

为了验证本文提出的EMD-DSVR预测方法的有效性，利用社会媒体数据对上证指数和深成指数从2013年4月1日到2014年3月31日共240天的收盘值进行预测。

本文采用百度搜索指数功能获取社会媒体变量数据。百度搜索指数是百度网站提供的海量数据分析服务，用以反映网民在过去一段时间内利用百度搜索引擎对特定关键词的累计搜索频次。此外，将股指收盘值序列的前期值作为控制变量加入预测模型中。由于具有初值敏感性，混沌时间序列只适合做短期预测，因此将股票收益序列的前200个数据点为训练集，后40个点为测试集，仅做一步预测，用均方根误差衡量模型的预测性能。

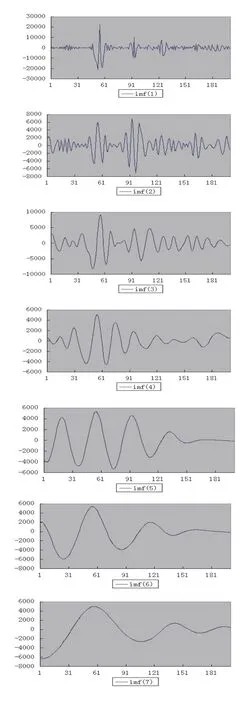
图2　社会媒体变量序列EMD分解结果

将上证指数作为，获取其百度搜索指数的时间序列Data1。图2是对Data1进行EMD分解的结果，共产生7个基本模态分量imf(i)，i=1,2, ... ,7。根据对各个imf的混沌相空间重构，设计前层支持向量回归机的结构。在此需要计算Data1各模态分量的最佳延迟时间和嵌入维数。通过计算互信息值，得出Data1各模态分量的延迟时间；将求得的延迟时间代入FNN算法，经计算可得各模态分量的假近邻率，由此得出各序列的嵌入维数。表1展示了Data1各模态分量的最佳延迟时间、嵌入维数和最大Lyapunov指数。通过Lyapunov分析，各模态分量的最大Lyapunov指数均大于0，这表明各模态分量均具有不同程度的混沌性[21]，适用于混沌分析的应用场景。

表1　社会媒体变量序列各模态分量的混沌参数

根据得出的混沌参数，对Data1的各模态分量进行混沌序列的支持向量回归建模，前层支持向量回归机的核函数选用Puk核函数。由于本文只进行一步预测，因此对于各模态分量，每预测一个值以后，需要在百度搜索指数序列中加入与预测分量对应的百度指数实际值，并重新进行EMD分解，产生各模态分量的实际值，然后根据构建的混沌支持向量回归模型继续预测各模态分量的下一个数据点。对于长期趋势项，由于其形态接近线性函数，根据线性拟合法对其进行预测。此外，根据相关系数检验，上证指数收盘值序列具有一阶自相关性，因此将前一期的收盘值作为控制变量，与各模态分量和长期趋势的预测值一同输入后层支持向量回归机中，得到最终的预测结果。后层支持向量回归机采用多项式核函数。对深成指数做同样的分析预测。图3显示了本文提出的EMD-DSVR模型的预测效果。

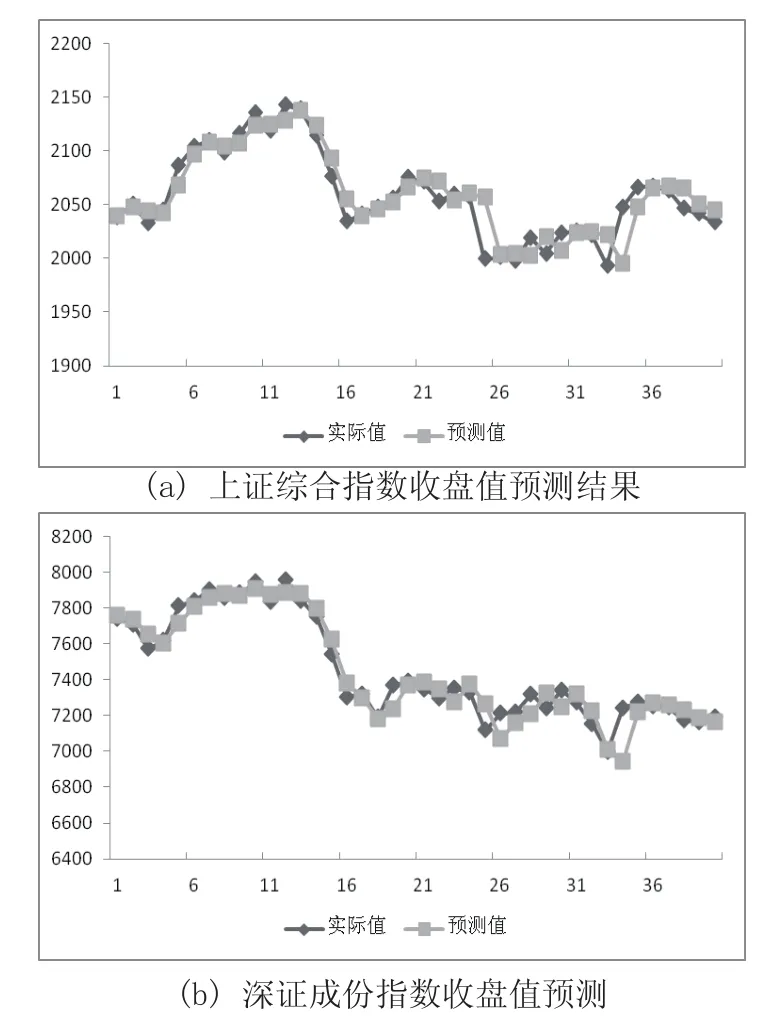
图3　两市日收盘值预测结果

从图3可以看出，在对上证指数收盘值的预测中，前21个点的预测效果较好，从第22个点开始预测精度逐渐降低，预测值的变化较之实际值的变化出现滞后。深成指数的预测也出现了类似的情况，从第19个点开始，预测误差逐渐变大并出现预测滞后。造成这种现象的原因可能与混沌序列建模有关。虽然本文对两市收盘值采用了一步预测的策略，即所有解释变量均为实测数据。然而，在训练集上对社会媒体变量序列各模态分量的混沌支持向量建模是一次性的，随着时间的推移，适用于训练集上的混沌参数（延迟时间和嵌入维数）不一定再适合于新的测试数据，此时社会媒体变量对股指收盘值的解释能力开始减弱，EMD-DSVR模型的预测能力逐渐依赖于控制变量，即收盘值的自相关前期值。所以，在对后面点的预测中，精度逐渐降低并出现了滞后现象。

为了验证本文提出的EMD-DSVR方法的预测性能，对所选实验数据，再分别运用经典的人工神经网络模型（ANN）和支持向量回归模型（SVR）进行预测，并比较我们提出的方法与ANN和SVR模型各自的均方误差，结果如表2所示。在运用ANN和SVR模型时，直接对社会媒体变量序列本身进行混沌序列的建模预测。由表2可知，无论是对上证指数还是深成指数，本文方法的预测误差均小于其他两类模型，预测性能最优。

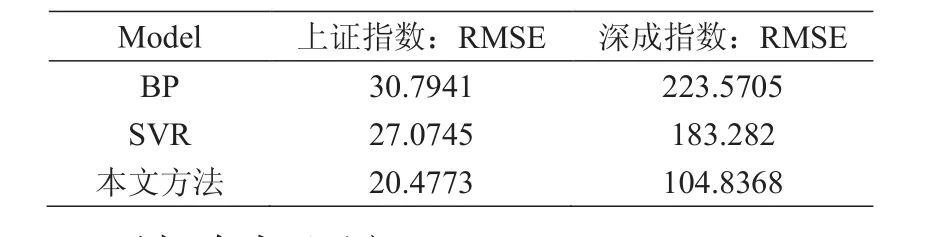
表2　不同模型的均方根误差比较

3　 结论与展望

本文通过对社会媒体变量序列进行EMD分解和混沌支持向量回归建模，提出一个基于EMDDSVR的股指时间序列预测方法。应用该方法对上证综合指数和深证成份指数的收盘值进行预测，发现将社会媒体变量序列进行多尺度分解能有效地提高其对股票市场的预测性能，证明了所提出方法的有效性。然而，社会媒体具有多种类型，如论坛、博客和社交网络，同一社会媒体平台中又可以提取多种社会媒体变量，如情感倾向、主题评论数和转发次数等。如何运用EMD-DSVR方法验证不同社会媒体对股票市场的预测性能，以及多种社会媒体对股票市场产生的交互影响将成为我们未来的研究工作。

[1]李爱忠,任若恩,董纪昌. 基于集成预测的均值-方差-熵的模糊投资组合选择[J]. 系统工程理论与实践,2013（05）:1116-1125.

[2]Das S R, Chen M Y. Yahoo! for Amazon: sentiment extraction from small talk on the web[J]. Management Science, 2007（53）: 1375–1388.

[3]Antweiler W, Frank M Z. Is all that talk just noise? The information content of internet stock message boards[J]. Journal of Finance, 2004（59）: 1259–1294.

[4]Bollen J., Mao H., Zeng X. Twitter mood predicts the stock market[J]. Journal of Computational Science, 2011,2 (1) :1-8.

[5]Chen Hsinchun. AI and Opinion Mining[J]. IEEE Intelligent Systems, 2010, 25（3）:74-76.

[6]CQ Jiang, et al. Analyzing market performance via social media: a case study of a banking industry crisis[J]. Science China Information Sciences, 2014, 57（5）:1-18.

[7]X Zhang, H Fuehres, P Gloor. Predicting Asset Value Through Twitter Buzz[J]. Advances in Intelligent and Soft Computing, 2012(113)：23-34.

[8]王文波, 费浦生, 羿旭明. 基于EMD与神经网络的中国股票市场预测[J]. 系统工程理论与实践,2010（06）:1027-1033.

[9]Peter E E. Fractal Market Analysis: Applying Chaos Theory Investment and Economics[M]. New York: John Wiley and Son,1996.

[10]S R Mudakkar, K Zaman. A wavelet analysis of oil prices and stock market: Evidence from Pakistan and India[J]. Energy Policy. Article in Press.

[11]Vuorenmaa, Tommi A. A wavelet analysis of scaling laws and long-memory in stock market volatility[C]. Proc. SPIE 5848, Noise and Fluctuations in Econophysics and Finance, doi:10.1117/12.626343.

[12]Jammazi, Rania. Wavelet decomposition and regime shifts: Assessing the effects of crude oil shocks on stock market returns[J]. Energy Policy, 2010, 38(3): 1415-1435.

[13]Fernández-Macho, Javier. Wavelet multiple correlation and cross-correlation: A multiscale analysis of Eurozone stock markets[J]. Physica A: Statistical Mechanics and its Applications. 2012, 391(4): 1097-1104.

[14]Langi, A. Z R, Pitara, S.W., Kuspriyanto. Stock prices trends analysis using wavelet transform[C]. 2012 International Conference on Cloud Computing and Social Networking, doi: 10.1109/ICCCSN.2012.6215753.

[15]Gallegati, Marco. A wavelet-based approach to test for financial market contagion[J]. Computational Statistics and Data Analysis, 2012, 56(11): 3491-3497.

[16]Tewfiki A H. On the optimal choice of a wavelet for signal representation[J].IEEE Trans Information Theory, 1992,38(2):747-765.

[17]N E Huang,Z Shen,S R Long. A new view of nonlinear water waves—The Hilbert spectrum[J]. Annu.Rev.Fluid Mech.1999.31:417-457.

[18]吕小青. 确定延迟时间互信息法的一种算法[J].计算物理,2006,23(2):184-188.

[19]Karatasou, S. Santamouris, M. Detection of low-dimensional chaos in buildings energy consumption time series[J]. Communications in Nonlinear Science and Numerical Simulation, 2010, 15(6):1603-1612.

[20]苑莹, 庄新田. 金融时间序列的标度特性实证研究[J]. 管理工程学报, 2008(2): 85-89.

[21]盛昭瀚, 马军海. 管理科学:面对复杂性—混沌时序经济动力系统重构技术[J]. 管理科学学报. 1998 (01): 31-42.

Prediction Method of Stock Market Based on EMD-DSVR under Social Media Environment

LIANG Kun1, ZHANG Lizheng2
(1.School of Management, Hefei University of Technology, Hefei，230009, China, 2.School of Management，AnHui Jianzhu University，HeFei，230022，China)

The existing relevant research of social media-based market performance analysis fails to consider the multi-scale of stock time series. To solve this problem, by employing the empirical mode decomposition (EMD), chaos theory and support vector regression, this paper presents an EMD-DSVR method to predict stock market. First, the intrinsic link between stock time series multi-scale and social media time series multi-scale has been analyzed; and by using EMD method, this paper decomposes the social media time series into many intrinsic modal function (IMF) which can significantly represent potential information of original time serial. Then, by using chaos theory and support vector regression, this paper predicts and sets models for each IMF. Finally, market performance is predicted by using the IMF of social media time series. In order to verify the effectiveness of EMDDSVR model, the close value of Shanghai Composite Index and Shenzhen component index are predicted by using this model. The results show that our approach can effectively improve the prediction accuracy of stock time series.

empirical mode decomposition; stock time series; chaos theory; support vector regression

TP391

A

2095-8382(2016)05-106-05

10.11921/j.issn.2095-8382.20160519

2015-10-12

国家自然科学基金重点项目(71331002)，教育部博士学科点专项科研基金(20120111110027)，安徽省软科学重大项目(1302053009)

梁坤(1985-)，男，博士生，主要研究方向为社会媒体分析与预测.