带参数的四阶时滞微分方程的边值问题
蹇玲玲,郭晓晔
(青岛理工大学琴岛学院)
带参数的四阶时滞微分方程的边值问题
蹇玲玲,郭晓晔
(青岛理工大学琴岛学院)
通过构造一个新的锥,研究了带参数的四阶时滞微分方程的边值问题.
带参数的四阶时滞微分方程;边值问题;锥;不动点
0 引言
该文研究非线性四阶时滞微分方程的边值问题
(1)
其中λ>0,h:[0,1]×[0,∞)2→[0,∞)为连续函数.将文献[1]中的带参数的二阶时滞微分方程的边值问题进行了推广.
如果令
v=-u″,g(t,u(t-τ),v(t-τ))=v,
f(t,u(t-τ),v(t-τ))=h(t,u(t-τ),-v(t-τ)),则问题(1) 等价于下列二阶时滞微分方程系统

(2)
其中f,g:[0,1]×[0,∞)2→[0,∞)为连续函数.所以要证明问题(1) 解的存在性只需证明二阶时滞微分方程系统解的存在性.
为得到该文的主要结论, 首先令
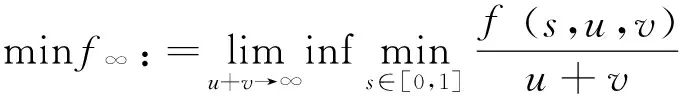

1 预备知识和引理
假设(u,v)是问题(2)的解,则
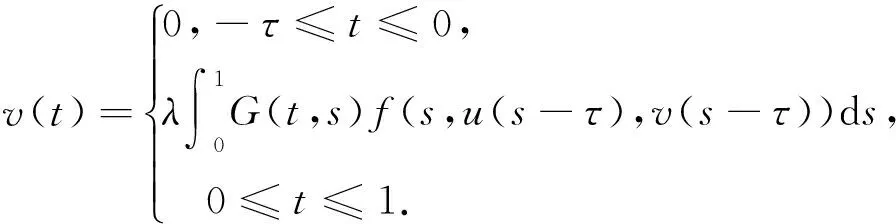

令E={(u,v)∈C[-τ,1]×C[-τ,1]:u(t)=v(t)=0,∀t∈[-τ,0]:u(1)=
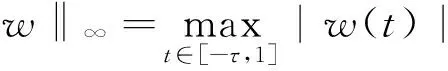

则问题(2)等价于不动点方程F(u,v)=(u,v).
引理1 算子F:E→E是全连续算子,且F(K)⊂K.
2 主要结果及证明

则问题(2)至少存在三个正解.
为了证明该定理,首先给出如下引理.
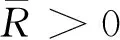
引理2 假设条件(H1)成立,且minf∞>0,则存在R1>0,Λ1>0,使得当λ>Λ1时,有
‖F(u,v)‖≥‖(u,v)‖,(u,v)∈∂CR1
证明 对∀ε>0,由minf∞>0知,存在
f (s,u,v)≥(minf∞-ε)(u+v),∀s∈[0,1]
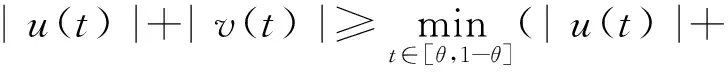
从而
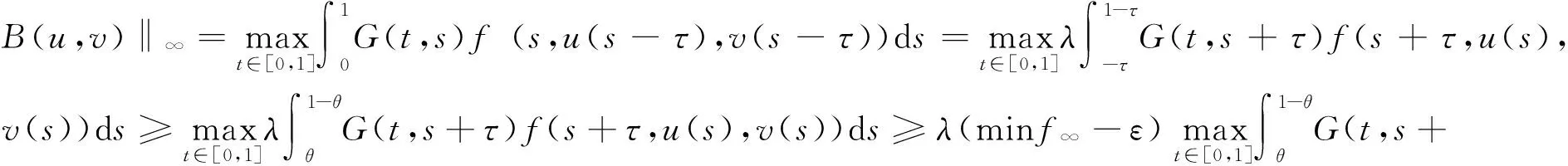
故存在Λ1>0,当λ>Λ1时,‖F(u,v)‖=‖A(u,v)‖∞+‖B(u,v)‖∞≥‖B(u,v)‖∞≥‖(u,v)‖.
引理3 假设条件(H1)成立,对上述R1>0,λ>0,有λmaxf0+maxg0<8,则存在R2∈(0,R1),使得‖F(u,v)‖≤‖(u,v)‖,(u,v)∈∂CR2.
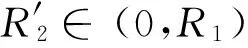
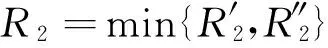
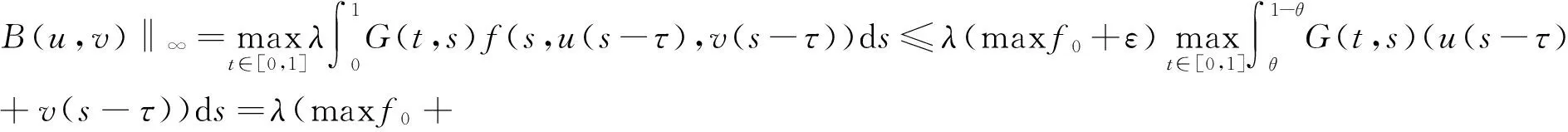

‖F(u,v)‖=‖A(u,v)‖∞+
引理4 假设条件(H1)成立,且minf0>0,则对上述R2>0,存在R3∈(0,R2),Λ2>0,使得λ>Λ2时, ‖F(u,v)‖≥‖(u,v)‖,(u,v)∈∂CR3.
证明 ∀ε>0,由minf0>0,存在R3>0,当0≤u+v≤R3时,
f(s,u,v)≥(minf0-ε)(u+v),∀s∈[0,1]
则对(u,v)∈∂CR3,
故存在Λ2>0, λ>Λ2时, ‖F(u,v)‖≥‖(u,v)‖.
引理5 假设条件(H1)成立,对上述R1>0,λ>0,λmaxf∞+maxg∞<4,则存在R4>R1, ‖R(u,v)‖≤‖(u,v)‖,(u,v)∈∂CR4.

(u+v),由maxg∞<∞,存在R4″>R1, u+v≥R4″时, g(s,u,v)≤(maxg∞+ε)(u+v)

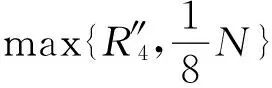
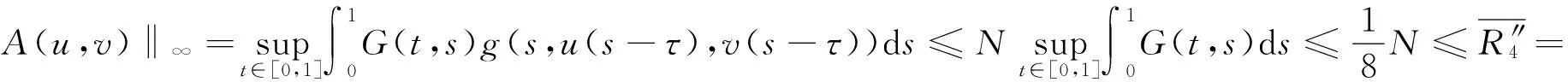


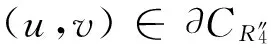

A[2]可知,系统(2)存在三个正解(u1,v1),(u2,v2),(u3,v3)满足R3<‖(u1,v1)‖ [1] 蹇玲玲. 带参数的二阶时滞微分方程的边值问题[J]. 哈尔滨师范大学自然科学学报, 2015, 31(5): 11-15. [2] Bai Dingyong, Xu Yuantong. Existence of positive solutions for boundary-value problems of second-order delay differential equations[J]. Applied Mathematics Letters, 2005,18:621-630. (责任编辑:季春阳) Boundary Value Problems for Forth Order Delay Differential Equations with Parameter Jian Lingling, Guo Xiaoye (Qingdao Technological University) In this paper, the existence of solutions for forth order delay differential equations with parameter is proved by constructing a new cone. Forth Order Delay Differential Equations with Parameter; Boundary Value Problems; Cone; Fixed point 2016-02-02 0175.8 A 1000-5617(2016)02-0057-03

