具有垂直传染的SEIR疾病模型的分支方向

于莉琦

(黑龙江东方学院)



具有垂直传染的SEIR疾病模型的分支方向

于莉琦

(黑龙江东方学院)

在具有垂直传染的SEIR疾病模型中引入了时间延迟，当时间延迟到达或穿过临界值时，系统在正平衡点附近出现了一族周期解.应用规范型和中心流形理论给出决定该模型分支方向及分支周期解稳定性的显示表达式.

Hopf分支；稳定性；周期解

在文献[1]中，Li Michiael Y和Wang L研究了一个具有垂直传染的SEIR疾病模型，具有这种特征的疾病如风疹，疱疹等，模型经简化[1]如下，其中S表示易感人群，E表示携带者(未发病)人群， I表示患者人群，

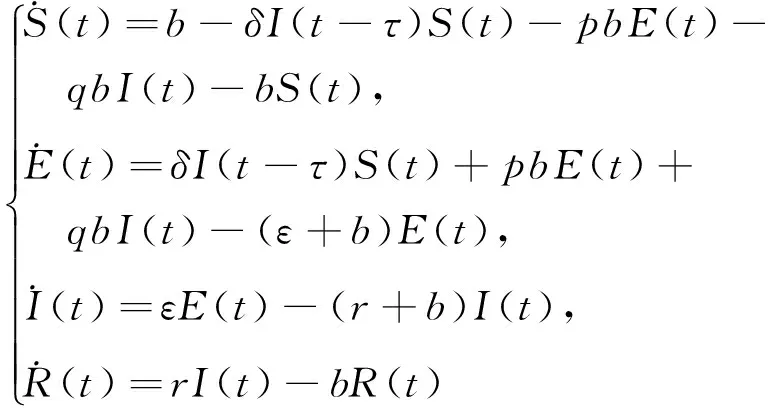
(1)

在系统(1)中引入时间延迟τ，得到时滞系统

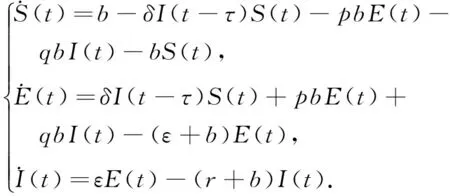
(2)

当时间延迟τ到达或穿过临界值τ(j)(其中τ(j)如文献[2]中定义)时在正平衡点附近出现了一族周期解，当τ=τ(j)时系统(2)在正平衡点处出现了Hopf分支，下面应用标准形理论和中心流形理论来研究分支周期解的稳定性[3-7].

令系统的正平衡点为 S*，E*，I*，u1(t)=S(t)-S*,u2(t)=E(t)-E*,u3(t)=I(t)-I*,xi(t)=ui(τt),τ=τ(j)+μ,μ∈R,系统(2)等价于系统

(3)

此时该系统(3)具有平衡点(0,0,0).

系统(3)可等价为一个C=C([-1,0],R3)中的泛函微分方程

(4)

其中xt(θ)=x(t+θ)∈C，且Lμ:C→R,F:R×C→R定义如下：

Lμ(φ)=(τ(j)+μ)×

(5)

其中φ(θ)=(φ1(θ),φ2(θ),φ3(θ))T∈C，由文献[2]知，当μ=0时系统(3)的特征方程有一对纯虚根±iτ(j)ω0，且横截条件成立，系统在零平衡点处出现了Hopf分支.由Riesz表示定理，存在着分量为有界变差函数的三阶矩阵η(θ,μ)

(6)

事实上，只要取

η(θ,μ)=(τ(j)+μ)×

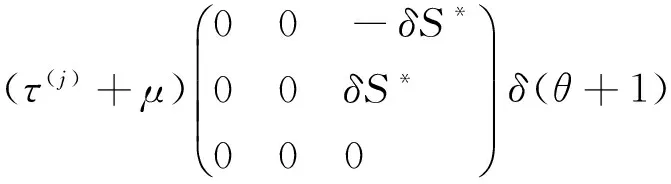
(7)

即可，对φ∈C1([-1,0],R3)，定义

这样方程(4)可写成如下形式

(8)

其中，对于任意ψ∈C([0,1],(R3)*)，定义

和双线性内积

(9)

其中η(θ)=η(θ,0).则A(0)与A*互为共轭算子.令q(θ)=(1,α,β)Teiθω0τ(j)是A(0)关于iτ(j)ω0的特征向量，即A(0)q(θ)=iτ(j)ω0q(θ)，计算得

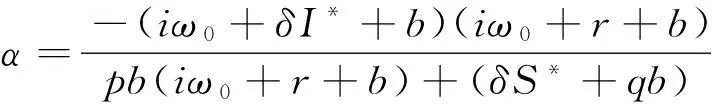
同理设q*(s)=D(1,α*,β*)eiθω0τ(j)是A*关于-iτ(j)ω0的特征向量，计算得

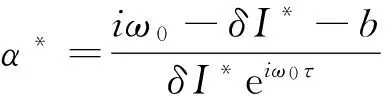
由双线性内积=1可将q*规范化.令xt为(4)式在μ=0时的解，定义，

z(t)=,W(t,θ)=xt(θ)-2Re{z(t)q(θ)}

(10)

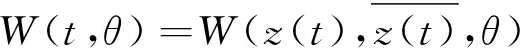
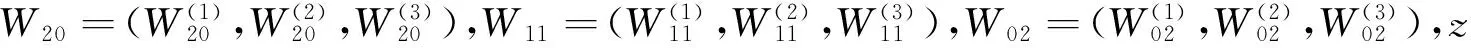
(11)

其中

(12)

其中xt(θ)=(x1t(θ),x2t(θ),x3t(θ))T=

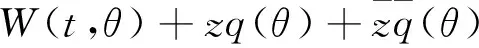
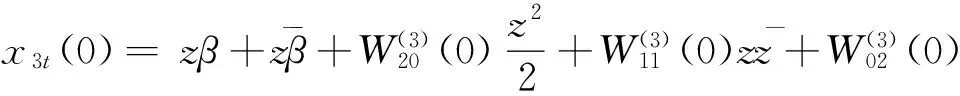
根据(11)式，得

将x1t(0),x3t(0),x1t(-1),x3t(-1)代入得

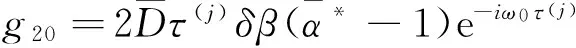
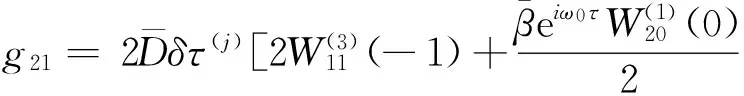
为了确定g21，需要计算W20(θ),W11(θ)， 由方程(10)，(11)得

(13)

(14)

(A-2iτ(j)ω0)W20=-H〗20(θ),

AW11(θ)=-H11(θ)

(15)

对于任意的θ∈[-1,0)，

(16)

与(14)比较系数得

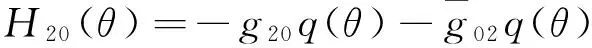
由(13)(15)及矩阵A，得到

(17)

因q(θ)=(1,α,β)Teiθω0τ(j)，有

(18)

(19)

其中η(θ)=η(θ,0)，则

注意到

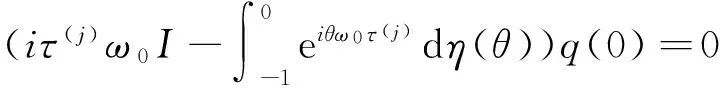
定理：对于系统(3)应用规范型和中心流形定理给出参数gij的计算公式，从而可以计算下列参数的值.

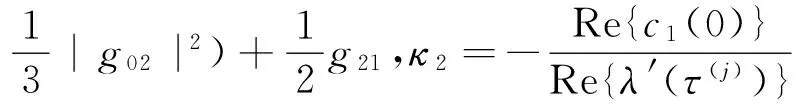
β2=2Re{c1(0)},

这几个参数决定了系统当分支值变化到τ(j)时的分支方向及分支周期解的相关性质，κ2决定了分支的方向：κ2>0，分支是上临界的，分支周期解在τ>τ(j)时出现，κ2<0，分支是下临界的；分支周期解在τ<τ(j)时出现，β2决定了分支周期解的稳定性，β2<0，中心流形上的周期解是稳定的，否则是不稳定的，T2决定了分支周期解的变化：T2>0，周期解的周期是增加的，否则是减少的.

[1] Michael Y Li, Hal L. Smith and Liancheng Wang. Global Dynamics of An Seir Eqidemic Model with Vertical Transmission. SIAMJ.App Math,2001,62:158-169.

[2] 于莉琦. 具有垂直传染的SERI疾病模型的Hopf分支分析[J]. 生物数学学报，2015，30(4)：753-757.

[3] Feichtinger G, Forst C V, Piccardi C. A nonlinear Dynamical Model for the Dynastic Cycle[J]. Chaos Solitons & Fractals, 1996,7(2): 257-271.

[4] Wei Junjie, Li Michael Y. Global Existence of Periodic solution in A Tri-neuron Model with Delays[J]. Physical D, 2004,198(1):106-119.

[5] Rebecca V, Culashaw, Ruan Shigui. A Delay-differential Equation Model of HIV Infection of CD4 T-cells[J]. Mathematical Biosciences,2000,165(1):27-39.

[6] Song Yongli, Han Maoan, Wei Junjie. Stability and Hopf Bifurcation Analysis on a Simplified BAM Neural Network with Delays[J]. Physical D, 2005,200(1):185-204.

[7] Ding Xiaohuan, Li Wenxue. Local Hopf bifurcation and global existence of periodic solutions in a kind of physiological system[J]. Nonlinear Analysis:Real World .

(责任编辑：于达)

The Direction of Hopf Bifurcation and Stability of SEIR Eqidemic Model with Vertical Transmission

Yu Liqi

(East University of Heilongjiang)

The delay to the SEIR Eqidemic Model with Vertical Transmission is introduced in this paper. The positive equilibrium’s stability changes when the delay cross a sequence of critical values in the dynamical model of the dynastic cycle with delay. The normalform theory and center manifold argument are employed, the explicit formulas determining direction and other properties of bifurcation periodic solutions are given.

Hopf bifurcation; Stability; Periodic solution

2016-01-20

O29

A

1000-5617(2016)02-0043-04