一致稳定矩阵的约束逆特征值问题*

刘 巍，王柏育

(长沙学院)



一致稳定矩阵的约束逆特征值问题*

刘 巍，王柏育**

(长沙学院)

研究了关于一致稳定矩阵的约束逆特征值问题及其最佳逼近问题. 利用矩阵的奇异值分解，给出了一致稳定矩阵的约束逆特征值问题有解的充要条件以及解的一般表达式，最后得到了相应的最佳逼近问题的解的表达式.

一致稳定矩阵；约束逆特征值；最佳逼近问题

0 引言

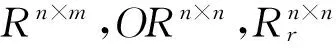
(1)

其中U=(U1U2)∈ORn×n,V=(V1V2)∈ORm×m,U1∈Rn×r,R(U2)=N(XT),V1∈Rm×r,∑=diag(σ1,σ2,…,σr),σ1≥σ2≥…≥σr.

定义1 如果n×n实矩阵A的所有特征值的实部都小于0，称矩阵A是稳定矩阵，如果n×n实矩阵A的所有特征值的实部都小于等于0，称矩阵A是半稳定矩阵，如果n×n实矩阵A+εI,(ε>0)的所有特征值的实部都小于等于0，称矩阵A是一致稳定矩阵.

该文主要讨论以下两个问题:

问题Ⅰ(约束逆特征值问题) 给定α>0. 令

hj<0,λk<0,j=1,…,p,k=2p+1,…,m.

求矩阵A使得集合SE={A|AX=XΛ,A∈Sε(n)}非空，以及求集合SE的某个子集SE(α)使得SE(α)中每个矩阵的剩余特征值都位于半径为α的闭圆盘Dα内， 其中ε=min{|hj|,|λk|,j=1,…,p,k=2p+1,…,m},Sε(n)=

{A|Re(λ(A+εI))≤0,A∈Rm×n}.

问题Ⅱ (最佳逼近问题) 给定B∈Rn×n.求AB∈SE(α)使得

对于不同矩阵集合约束的逆特征值问题AX=XΛ，已经有很多结果，张磊和潘小平在文献[4-6]中, 讨论了相应的约束逆特征值问题, 并且给出了在实轴和虚轴上的一般解的表达式和相应的最佳逼近解.

1 问题Ⅰ的解

在该节中，根据矩阵的奇异值分解，给出了问题Ⅰ有解的条件以及解的一般表达式.

定理1[7]令X,Λ如问题Ⅰ中所定义, 则问题Ⅰ的解集SE非空的充要条件是

XΛX+X=XΛ

(2)

而且，如果A∈SE, 则

(3)

其中U,∑,V1如引理1中所定义,A12∈Rr×(n-r),A22∈Sε(n-r)是任意的.

下面将给出约束解集合SE(α).

定理2 令X,Λ如问题Ⅰ中所定义, 则问题Ⅰ的解集SE(α)非空的充要条件是XΛX+X=XΛ.

反之，假设存在矩阵A∈SE(α)使得AX=XΛ,则有‖AX-XΛ‖2=0.令矩阵X的奇异值分解如(1)式, 令

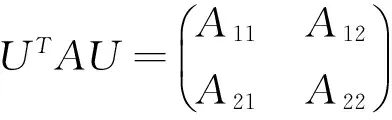
由引理1和Frobenius范数的正交不变性, 可得

(4)

(4)式可以也表示为

2 问题Ⅱ的解

在本节中，对给定的矩阵B，给出约束逆特征值问题的最佳逼近解.

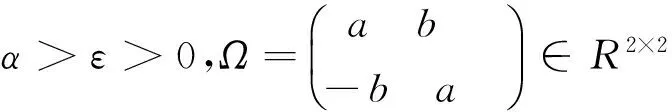
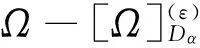
其中

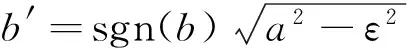
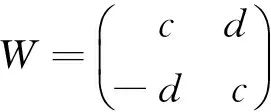
则a+ib，c+id分别是矩阵Ω和W的特征值. 令

情形2 π-φ≤θ≤π+φ,ρ(Ω)>α.因为

(5)

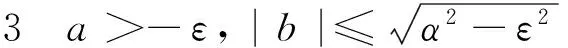
‖Ω-W‖2=2(a-c)2+2(b-d)2,

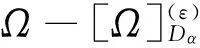
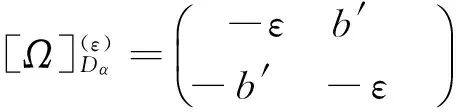
和

根据引理3, 可得

(6)

而且, 矩阵AB的表达式为

证明 设矩阵A∈SE(α),则有

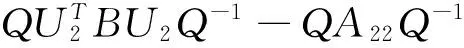
(7)

由(6)式, 可知(7)式成立当且仅当

令

[1] Haftka R T, Adelman H M. Recent developments in structural sensitivity analysis[J]. Structural optimization, 1989, 1:137-151.

[2] 张磊,谢冬秀. 一类逆特征值问题. 数学物理学报, 1993,13(1) :94-99.

[3] Hirsch M W, Smale S. Differential Equations, Dynamical Systems, and Linear Algebra[J]. Academic Press Inc,San Diego, CA, 1974:29-61.

[4] 张磊. 一类对称矩阵的逆特征值问题[J].高等学校计算数学学报, 1990,12 (1):65-71.

[5] Pan X P, Hu X Y, Zhang L. The solvability conditions for a class of constrained inverse eigenvalue problem of antisymmetric matrices[J]. Korean Math Soc, 2006,43(1) :87-98.

[6] Pan X P, Hu X Y, Zhang L. A class of constrained inverse eigenproblem and associated approximation problem for skew symmetric and centrosymmetric matrices[J]. Linear Algebra Appl, 2005,408:66-77.

[7] Liu W, Li D W, Lan Y. Inverse eigenvalue problem and associated approximation for uniform stable matrices[J]. Proceeding of the sixth international conference of matrices and operators, 2011(2): 155-158.The Constrained Inverse Eigenvalue Problem for Uniform Stable Matrices

(责任编辑：李家云)

Liu Wei，Wang Baiyu

(Changsha University)

In this paper, a kind of constrained inverse eigenvalue problem and associated optimal approximation problem for uniform stable matrices are studied. Based on the singular value decomposition, the sufficient and necessary conditions of the solvability and the general solutions of the constrained inverse eigenvalue problem are presented. Finally, the expression of the solution for the optimal approximation problem is obtained.

Uniform Stable Matrix; Constrained Inverse Eigenvalue; Optimal Approximation Problem

2015-12-15

*湖南省教育厅资助科研项目(15C0120)

**通讯作者：wangbaiyumath@163.com

O241.6

A

1000-5617(2016)02-0033-03