基于支持矩阵的频繁集增量更新算法改进研究*

纪怀猛，陆林花，黄风华

(阳光学院)



基于支持矩阵的频繁集增量更新算法改进研究*

纪怀猛，陆林花，黄风华

(阳光学院)

针对FUP算法在频繁集增量更新时，剪枝效率低下以及候选集验证速度慢的缺陷，提出了基于支持矩阵的频繁集增量更新的高效挖掘算法—SMFUP算法.该算法不仅采用支持矩阵进行整体剪枝来提高剪枝效率，而且进一步结合频繁2项集矩阵加快候选频繁集的验证速度，从而使算法的增量更新效率大大提高.最后通过实验证明了算法改进的有效性.

频繁集；关联规则；FUP；支持矩阵；增量更新

0 引言

近年来，电子商务的兴起促进了对个性化推荐系统研究.其中，在海量数据库中挖掘关联规则[1]是个性化推荐系统中一个非常重要的研究课题.

关联规则挖掘最经典的算法Apriori算法[2]算法自提出后，众多学者已对算法的挖掘效率进行了多方面的研究和改进，如：采用FP-tree压缩存放数据库的主要信息的FP-growth算法[3]，基于压缩矩阵的方法[4]、基于2项集支持矩阵的算法F2AM[5]等，但是这些算法都是针对数据库中数据不变的情况.但是在电子商务应用中，数据库中的数据是随时间不断变化的，因此如何设计高效的挖掘算法来管理、维护和更新规则库中的关联规则成为个性化推荐研究中必须解决的首要问题.

针对关联规则的增量更新问题，目前也有众多的研究，最具代表性的是Cheung 等提出的如FUP[6],FUP2[7], 冯玉才等提出的 IUA 和 PIUA[8]，但这些算法都需要多次扫描数据库，为提高更新速度，牛小飞提出了基于支持矩阵的UBM算法[9]，但是该算法只考虑原数据库中的频繁项目，而对新项目不够敏感；黄德才提出的PFUP[10]算法，该算法的不足之处在 于需要保存原数据库中每个频繁集对应的向量，这样浪费了巨大的内存空间.而且不管是何种算法，采用的都是将原数据库和新数据库截然分开的处理方式.

该文提出的基于支持矩阵的频繁集增量快速挖掘算法(Fast Updating Algorithm based on Support Matrix, SMFUP)，特别适合最小支持度和最小置信度都保持不变的情况下，数据库D被添加增量数据d时关联规则更新的情况.SMFUP算法将原数据库和新数据库既看成整体，通过支持矩阵进行整体剪枝大幅减少了候选频繁项集的产生；又适当区分，利用支持矩阵与频繁2项集向量来提高候选集验证的效率.实验证明，该算法的改进是行之有效的.

1 基本概念

设I={i1,i2,…,im}是m个不同项目的集合，每个事务T是项的集合，使得T⊆I，D是数据库事务的集合.

设A是一个项集，事务T包含A，当且仅当A⊆T.A在D中的支持数记为sup(A)，即sup(A)=|A|/|D|，表示D中包含A的事务数.如果sup(A)大于等于用户给定的最小支持度minsup，则称A为频繁项集.如果A为频繁项集，并且包含k个项目，则A称为频繁k项集.

定义1 每个项Ij的向量定义为：

Dj=(d1j,d2j,…,dnj)T

项Ij的支持度计数为：

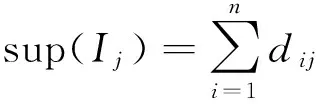
定义2 设事务数据库D中含有m个数据项，n个事务.令f:D→DM， DM=f (D)=(D1,D2,…,Dm)=(dij)m×n，其中：

其中，i=1,2,…,m;j=1,2,…,n.表示在事务数据库D中，如果第i个项出现在第j个事务中，则将矩阵DM第j行第i列的值为1，否则为0.

定义3 2项集{Ii,Ij}的向量定义为：

其中，“∧”是“逻辑与”运算符.

定义4 频繁2项集矩阵DM2定义如下：

DM2=(dm1,dm2,…,dmp)

其中，dmi为顺序生成的第i个频繁2项集对应的列向量.

定义5 频繁2项集支持矩阵M定义如下：

其中， w为频繁2项集{Ii,Ij}在DM2中对应列向量的编号.

2 基于支持矩阵的频繁集增量更新2.1 基于支持矩阵的频繁项集增量更新原理

2.2 SMFUP算法

算法假设源数据库D以矩阵形式存放.

输入 新增数据库d，最小支持度s

输出 满足最小支持度的所有D∪d的频繁项集

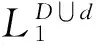
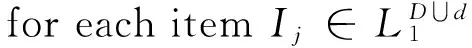
{由定义3计算Dij和dij;

if(Dij中1的个数+dij中1的个数≥s×

(|D|+|d|))

{DM2=(DM2,Dij);dM2=(dM2,dij);

Mij=w;w=w+1;

}

}

Step3 由频繁k项集增量挖掘频繁k+1项集.

k =2; //记Lk={Ik1,…,Ikmk}，Inew为Iki与Ikj连接后的项集

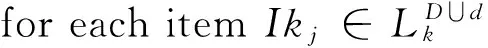
if(Iki与Ikj是可连接的) // 将Iki与ikj连接后的项集记为Inew

{if(Mij=0)

continue;

利用支持矩阵M、d以及dM2，计算出Inew在d中的支持数count1;

在D的频繁k+1项集中查找Inew;

if(Inew是D的频繁k+1项集)

if( count1+Inew在D中的支持数≥s×

(|D|+|d|))

Else

If(count1≥s×|d|

{利用支持矩阵M、D以及DM2，计算出Inew在D中的支持数count2;

If(count1+count2≥s×(|D|+|d|))

}

}

}

3 实验结果与分析

采用C++语言编写程序，采用安装了Windows XP SP3操作系统Pentium(R) Dual-Core CPU T4200主频2.00 GHz 2 GB内存的笔记本电脑为实验平台对SMFUP算法的性能进行了实验分析.实验采用的数据库为http://fimi.ua.ac.be/data中提供的Mushroom数据库，该数据库共有8 124条记录，119个属性；采用的增量数据分别为数据库的前200、400、600、800和1000条.将SMFUP算法与经典FUP算法的执行时间进行比较，两种算法的对比情况如图1所示.

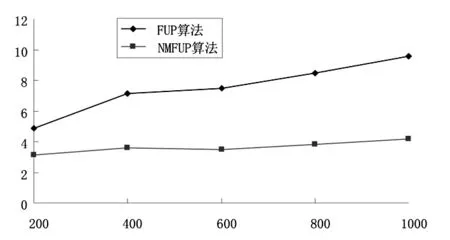
图1 两种算法执行时间对比

由图1可知，随着增量数据库d中记录数目的增加，FUP算法在验证候选频繁集时扫描的记录数随之增加，所以执行时间增长较快，而SMFUP算法在验证候选集是只需扫描各项目对应的相应列，并且采用了整体剪枝和频繁2项集矩阵加快了扫描速度，因此增量数据库中记录数的增加对其影响较小，所以扫描时间增加没有FUP明显.实验过程中，注意到增量600条记录时虽然新数据的加入使得频繁项集数大幅减少，但是FUP算法执行时间依然略有增加，但是SMFUP算法的执行时间却略有减少.实验结果表明，SMFUP算法执行效率明显优于FUP算法，这也充分证明了算法改进的有效性.

4 结束语

该文提出的SMFUP算法首先利用支持矩阵进行整体剪枝，最大限度地减少了候选项集的产生并加快了剪枝速度；然后采用支持矩阵和频繁2项集矩阵相结合的方式大大提高了算法验证候选频繁集的速度；最后，通过实验证明了改进算法的有效性.但是在电子商务的实际应用中，事务数据库D在记录数量上不仅可能随时间增加，有时还会因某种原因进行删除；而且最小支持度也可能会同时发生改变，因此设计能根据事务数据库的增减以及支持度的变化对数据库D进行高效增量更新挖掘的算法是下一步的研究方向.

[1] Agrawal R, Imielinaki T, Swami A. Mining Association Rules Between Sets of Items in Large Databases[C].Proc. of ACM SIGMOD Conference on Management of Data. Washington D C, USA: ACM Press, 1993.

[2] Agrawal R, Srikant R. Fast Algorithms for Mining Association Rules[C].Proc. of VLDB’94. Santiago, Chile: [s. n.], 1994.

[3] Han Jiawei,Jian Pei,Yiwen Yin. Mining frequent patterns without candidate generation[J]. ACM SIGMOD Record, 2000(2) .

[4] Han Jiawei, Kamber M. 数据挖掘: 概念与技术[M]. 范 明, 孟小峰, 译. 北京: 机械工业出版社, 2004.

[5] 纪怀猛.基于频繁2项集支持矩阵的Apriori改进算法[J].计算机工程, 2013,39(11):183-186.

[6] Cheung D W, Han Jiawei, Ng V, et al. Maintenance of discovered association rules in large database: an incremental updating technique[C]. Proceeding of 12th International Conference on Data Engineering, New Orleans, Louisiana, 1996: 106- 114.

[7] Cheung D, LEE S, Kao B.A general incremental technique for maintaining discovered association rules[C].Proceedings of the 5th International Conference on Database Systems for Advanced Applications, Melbourne, Australia, 1997.185- 194.

[8] 冯玉才, 冯剑琳.关联规则的增量式更新算法[J].软件学报, 1998, 9(4) : 301- 306.

[9] 牛小飞,刘浩,牛学东等.基于矩阵的关联规则增量更新算法[J].计算机工程与应用,2006,42(21):169-171,206.

[10] 黄得才,张良燕,龚卫华,等. 一种改进的关联规则增量式更新算法[J]. 计算机工程,2008,34(10):38-39,42.

(责任编辑：季春阳)

Improvement Research about Frequent Itemsets Incremental Updating Algorithm Based on Support Matrix

Ji Huaimeng, Lu Linhua, Huang Fenghua

(Yango College)

The efficiency is greatly reduced when the algorithm named FUP is used in incremental updating frequent sets. Because it’s low speed of candidate frequent set validation and pruning. The algorithm named SMFUP based on support matrix is put forward, using for efficiently mining incremental updating frequent item sets. The efficiency of the algorithm is greatly increased, because it is not only used to support matrix to speed up pruning; but also used 2- frequent item sets and support matrix to speed up candidate frequent set validation . Finally, the experiments show that the algorithm has a better performance than the FUP algorithm.

Frequent Itemsets; Association Rules; FUP; Support Matrix; Incremental Update

2016-01-09

*国家自然科学基金项目资助(41501451)

TP181

A

1000-5617(2016)02-0029-03