再生核结合Adomian分解法求解带有边值条件的二阶非线性微分方程*

闫丹丹,吕学琴

(哈尔滨师范大学)



再生核结合Adomian分解法求解带有边值条件的二阶非线性微分方程*

闫丹丹,吕学琴**

(哈尔滨师范大学)

研究求解带有边值条件的二阶非线性微分方程的方法. 文中利用再生核(RKM)理论结合Adomian分解法(ADM)来求解此类问题， 并且给出此类方法的收敛性分析及误差估计，同时通过算例说明该方法的可行性和有效性.

再生核空间；Adomian分解法；二阶非线性微分方程；误差估计

0 引言

考虑以下带有边值条件的二阶非线性微分方程

(1)

其中：ai(x),f(x)是区间[a,b]上的连续函数，α1,α2∈R，g(x,u)∈(C[a,b]×R).

非线性边值问题主要产生在有弹性和无弹性的流动、变形的粱方程、以及板极偏转理论的数学模型中[1-3]，并在工程技术、化学工程、热弹性学、周期轨道以及非线性机械震荡器，疾病的预测、人口流动问题中都有广泛的研究，国内外众多学者都在热衷于从事寻找这类微分方程数值求解的算法，如非线性微分方程反问题的数值解法[4]. 因此，基于再生核空间理论结合Adomian分解方法， 给出求解一类带有边值条件的二阶非线性微分方程的数值方法. 文中不仅通过算例说明此方法的有效性， 而且将会给出详细的收敛性分析和误差估计证明.

1 预备知识

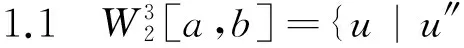
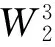
(2)

(3)

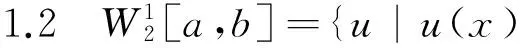
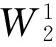
(4)

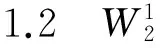
(5)

2 主要结果

2.1 RKM和ADM结合

(6)

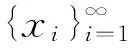
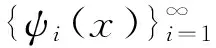
(7)

其中βik是正交化系数， βii>0,i=1,2,…

定理2.1 设u(x)是方程(1)的解，则

(8)

其中F(xk)=f(xk)-g(xk,u(xk)).

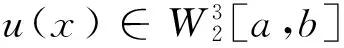
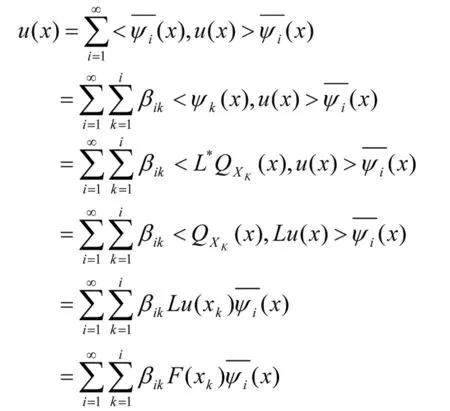
对Fourier级数截断，得到近似解Un(x)的表达式

(9)

对方程(6)左右两边同时作用L-1，得

u(x)=L-1f (x)-L-1g(x,u)

(10)

引入Adomian分解方法，给出u(x)和非线性项g(x,u)的级数形式

(11)

这里Ai是Adomian多项式且表达形式如下

将方程(11)代入(10)中得

(12)

通过Adomian分解方法，精确解u(x)的成分有下面的循环关系

(13)

当u(x)的成份ui(x)确定后，级数解可立刻获得. 为了计算求解的目的，可将级数解进行截断，得到近似解Un,N的表达形式

(14)

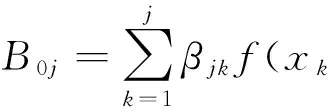
2.2 收敛性分析和误差估计

假设u(x)在x∈[a,b]上是有界的，非线性项g(x,u)满足Lipschitz条件‖g(u)-g(v)‖≤

L|u-v|在文献[5]中给出Adomian多项式满足下式

(15)

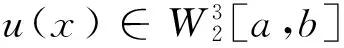
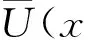
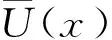
证明 (Ⅰ)首先证明Un(x)的收敛性，令Un和Um是任意的部分和，并且m≥n，可以得到Um是再生核空间上的柯西列.

‖Um-Un‖ =‖L-1[g(Um-1)-g(Un-1)]‖

又由于L-1的有界性以及g(u)满足的Lipschitz条件，

‖Um-Un‖=‖L-1[g(Um-1)-g(Un-1)]‖≤M‖g(Um-1)-g(Un-1)‖≤ML‖Um-1-Un-1‖

所以

‖Um-Un‖≤α‖Um-1-Un-1‖

当m=n+1时，

‖Un+1-Un‖≤α‖Un-Un-1‖≤α2‖Un-1-Un-2‖≤…≤αn‖U1-U0‖

根据三角不等式性质得，

因为0<α=ML<1，可知1-αm-n<1，则

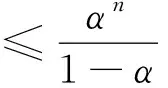
由‖u1(x)<∞‖，因此当n→∞，有

‖Um-Un‖→0

(Ⅱ)通过引理2.1和定理2.2(Ⅰ)，可知

=u0(x)+u1(x)+u2(x)+…+un(x)+…

定理2.2 (误差估计)假设u(x)是方程(1)的解，Un是方程的近似解，则

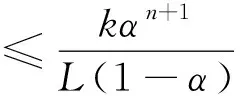
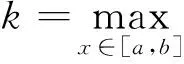
证明 通过定理2.2(Ⅰ)，有

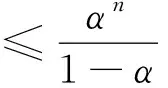
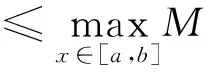
这样

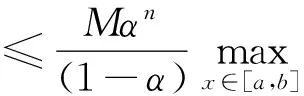
下面给出算例，证明此方法的有效性.

3 数值算例

例1 考虑下面带有边值条件的二阶非线性微分方程问题

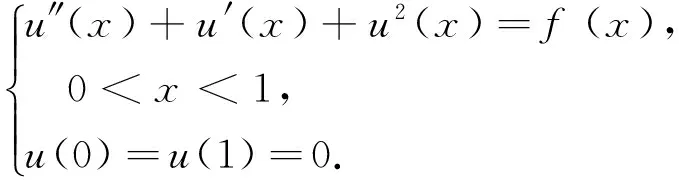
注意：通过表格可知，当N越大时，能得到更好的结果，这也充分证明了此方法的有效性及收敛性.

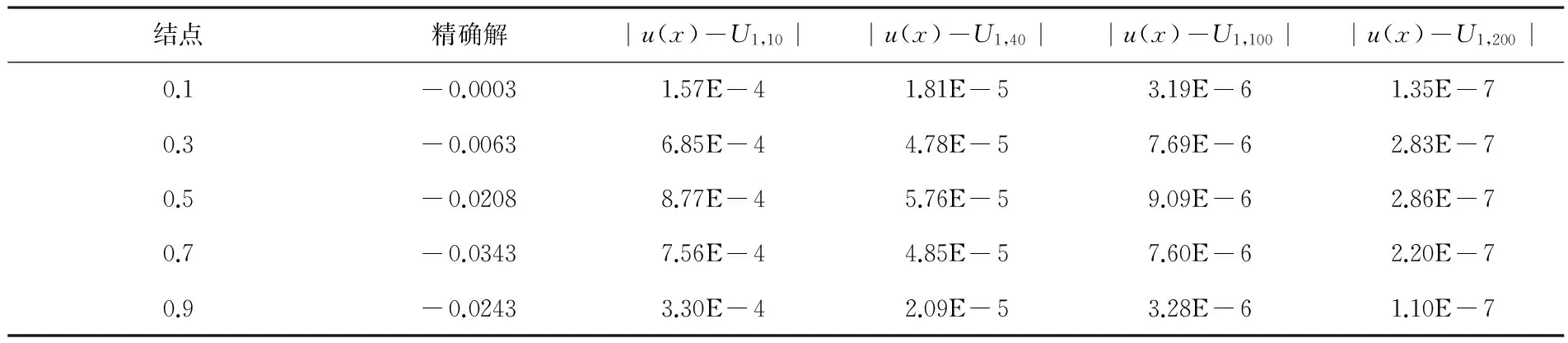
表1 精确解和绝对误差计算结果

[1] Du′acska E. Soil settlement effects on buildings[M]. In:Developments in Geotechnical Engineering Elsevier， Amsterdam, 1992.

[2] Soedel W. Vibrations of Shells and Plates[M]. New York，Dekker，1993.

[3] Henderson J，Tisdell C C. Dynamic boundary value problems of the second order Bernstein-Nagumo conditions and solvability[J]. Nonlinear Anal, TMA 2007, 67:1374-1386.

[4] 马宗立，岳素芳. 一类非线性微分方程反问题的数值解[J]. 哈尔滨师范大学自然科学学报，2007,23(5).

[5] El-Kalla I L. Convergence of Adomian’s method applied to a class of Vloterra type integro-differential equations[J]. Int J Didder Equ Appl ，2005(10)：225-234.

(责任编辑：于达)

The Combined RKM and ADM for Solving Second-order Nonlinear Differential Equations with Boundary Value Conditions

Yan Dandan, Lv Xueqin

(Harbin Normal University)

In this article, the solution of second-order nonlinear differential equations with boundary value conditions is researched. Using the theory of regeneration nuclear (RKM) combined with Adomian decomposition method (ADM) this problem is solved, and convergence analysis and error estimation of such a method are presented, at the same time through the numerical example, the feasibility and validity of the method are showed.

Reproducing kernel space;Adomian Decomposition method; Second-order nonlinear differential equations; Error estimation

2016-01-22

*国家自然科学基金项目(11401145);黑龙江省青年基金项目(JJ2016QN0211)

**通讯作者：hashidalvxueqin@126.com

O175

A

1000-5617(2016)02-0001-04