基于点接触赫兹理论的圆柱齿轮弯曲应力有限元分析
王红香,熊林根
(中国电子科技集团公司第二十一研究所,上海 200233)
基于点接触赫兹理论的圆柱齿轮弯曲应力有限元分析
王红香,熊林根
(中国电子科技集团公司第二十一研究所,上海 200233)
基于点接触赫兹理论,计算出圆柱齿轮啮合接触域的大小、方向和接触力。利用Pro/E建立圆柱齿轮三齿实体模型,利用模拟出来的接触应力进行加载,基于有限元法对一个啮合周期内圆柱齿轮弯曲应力分布进行计算分析,并与实例进行对比,验证分析的正确性。
接触特性;有限元分析;圆柱齿轮;弯曲应力
0 引 言
利用ANSYS软件来模拟齿轮啮合分析,能为设计者在设计过程中参数的选择以及实际加工机床参数的调整等提供比较直观的判断,ANSYS软件是假设齿轮是刚性的基础上,并且只有一对相互啮合的齿,所以软件分析有一定的局限性。本文简要描述了基于点接触赫兹理论模拟圆柱齿轮的真实啮合域来计算圆柱齿轮弯曲应力的方法,并利用有限元法进行仿真。
1 基于点接触赫兹理论的齿轮传动的接触域计算
1.1 基于点接触的齿轮接触域的确定
在M点接触的两个不规则形状的弹性体(如图1所示),根据赫兹点接触理论,在法向施加力F的情况下相互接触,在公切面上弹性体接触面之间距离相同的点构成椭圆域Ω。根据压力与位移成正比的关系,轴向偏移最大点在椭圆域Ω中心处,其对应的接触压力因此也最大;同理,随着边缘到中心的位移逐渐增大,其对应的接触应力也逐渐增大,而在边缘上偏移量为零,所以压力也为零。假设外力F、弹性体外形和材料常数固定,接触域的形状和大小可以计算得出。
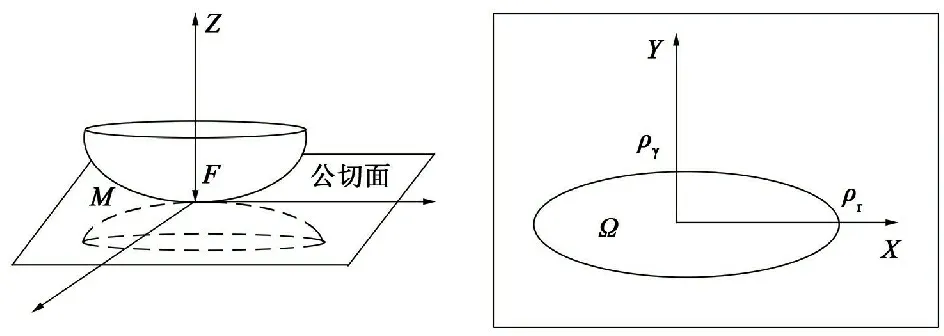
图1 接触模拟图
基于几何图形可知,物体表面到公切面上距离相等的点组成一个类椭圆域。基于接触点的弹性系数以及主曲率与椭圆域的关系可得,椭圆域长短轴需符合式(1):
(1)
式中:F为法向啮合力;θ1及θ2由弹性模量决定,θ的计算值由式(2)给出:
(2)
式中:m为拉伸系数。由于m=1/μ,则上式可化简:
(3)
式中:μi为泊松比;Ei为弹性模量,其中(i=1,2);u,v是基于τ(ρ)查询椭圆积分系数表得到的椭圆积分函数,
(4)
式中:K11、K12、K21、K22分别为两曲面在M点处的主法曲率;ω为两曲面主方向之间的夹角φ1。由上求出的椭圆域长短半径的大小可确定接触域的大小。
1.2 接触椭圆域长短轴方向的计算
确定的接触椭圆域长短轴方向,即诱导法曲率主方向的计算。以渐开线形式的齿轮为例,其曲面方程是以渐开线上的θ作为参数的。基于曲面切平面上的矢量计算方法可方便求出圆柱齿轮的两个主方向如下:
(5)
式中:θ10为圆柱齿轮渐开线起始点到齿槽对称线的角度;θ1为渐开线角度。该方向是基于小齿轮轴坐标系而得。
由主诱导法曲率和在该点两曲面主曲率之间的关系可知,e11,e12,e1,e2是位于公切面上矢量,为方便分析,以接触点作为坐标原点,如下图。
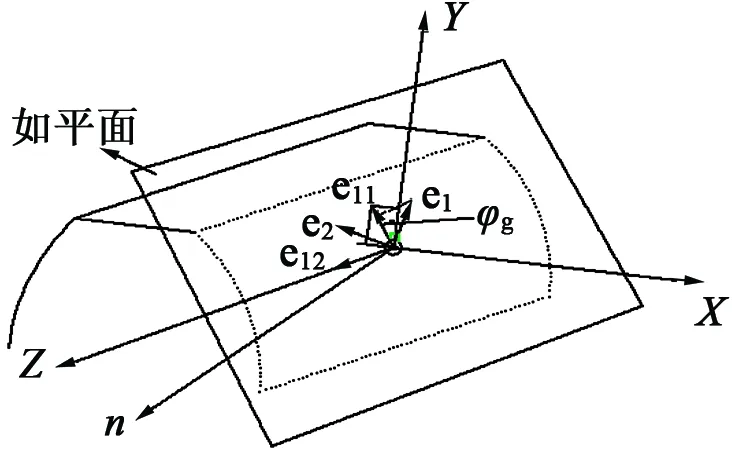
图2 诱导法曲率主方向分析坐标系
上图中φg为诱导法曲率主方向到圆柱齿轮主方向之间的转角 。
由式(5)在上图所示坐标系下可得诱导法曲率主方向如下:
(6)
1.3 啮合域应力分布
考虑椭圆接触区域由中心到边缘位移逐渐减小,因此相应的接触压力也逐渐减小,则在中心位置处压力最大,接触域边缘压力近乎为0。则载荷F在接触区域上是按近似半椭球体分布的,称之为法向应力椭球体,由下式决定:
(7)
式中:ρx为长轴半径;ρy为短轴半径。
当x=0,y=0时,给出最大应力如下:
(8)
用弹性系数θ1,θ2和主曲率K11,K12,K21,K22表示椭圆体长半径ρx和短半径ρy,则最大应力可表示:
(9)
2 齿轮传动弯曲应力在ANSYS软件上的分析实例
2.1 实例
给定小齿轮的参数如下:模数m=4,压力角α=20°,齿数N1=22,齿宽b=35 mm,与之啮合的圆柱齿轮的齿数为86。施加名义切向力Ft=1 000 N,选取圆柱齿轮三齿模型作为分析对象,利用ANSYS软件进行分析。
材料的弹性模量E取2.06×105MPa,泊松比μ为0.3。利用ANSYS工具,采取八节点四面体单元SOLID45对三齿模型进行网格划分。选用自由网格划分,确定接触域并对其进行网格局部细化,细化粒度在0.4 mm到0.7 mm之间,其他区域取单元棱长为1.5 mm。做过有限元颗粒度细化的模型如下图。最终面齿轮网格的单元数为40 379,节点数为8 172。
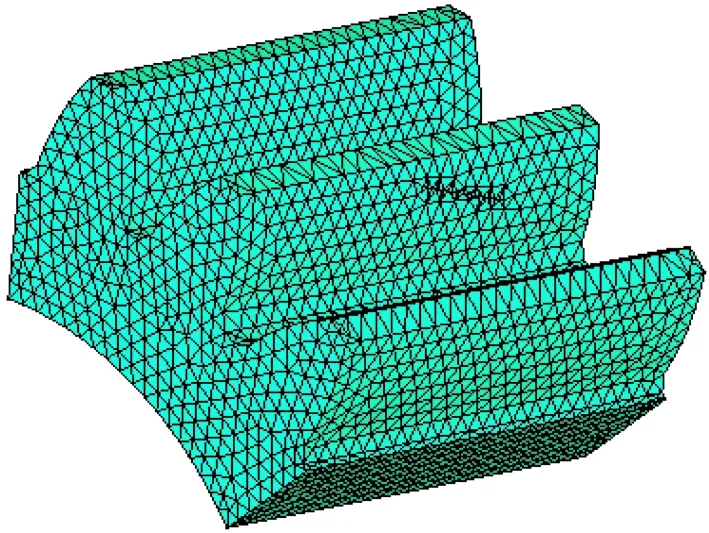
图3 圆柱齿轮模型网格图
以小齿轮开始啮合的转角做为参考基准,设为φ=0.2°,选择以下瞬态角度:齿底φ=2.7°,φ=5.3°,φ=7.8°,齿中φ=10.4°,φ=13.0°,φ=15.6°,齿顶φ=18.1°,φ=20.7°,φ=23.3°。
根据节1.1中的计算方法,在考虑齿间载荷分配的基础上,对接触域几何尺寸计算如表1。
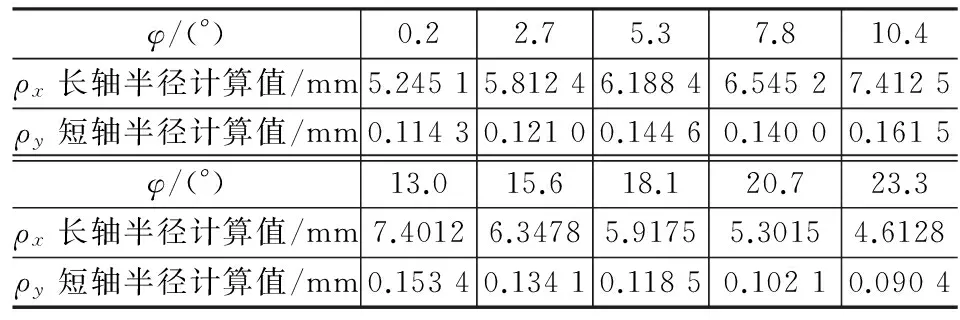
表1 各接触域长短轴大小
由表1中数值可得:
1)从齿根到齿顶,啮合域先变小后变大,在下半部达到最大值;
2)短轴远小于长轴,因此啮合域近似为分布在长轴上的线段。
根据节1.3中的计算方法,模拟齿轮啮合中的啮合域分布力如图4所示。在忽略齿间载荷分配的情况下,从齿根到齿顶啮合分布力逐渐变大,齿底位置啮合点接触域上分布力最小。
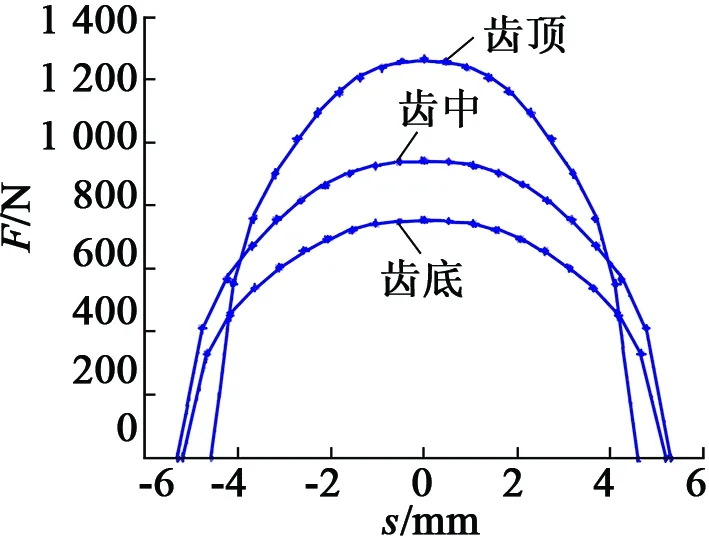
图4 啮合力模拟分布图
根据上述计算结果,对圆柱齿轮三齿模型进行齿面应力加载,得出弯曲应力分布图。图5是啮合转角在10.4°和23.3°时的弯曲应力分布图。
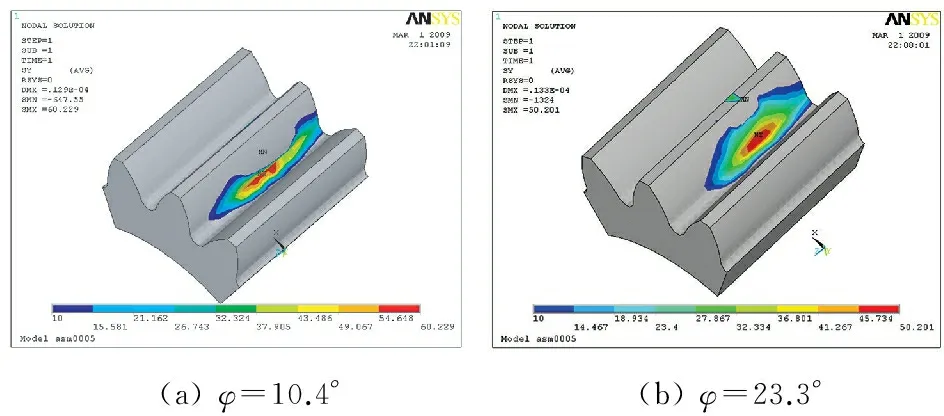
(a)φ=10.4°(b)φ=23.3°
图5 圆柱齿轮弯曲应力云图示例
利用ANSYS逐一仿真出上述10个啮合过程中的弯曲应力分布,并将统计结果计入表2。表中,σF为最大弯曲应力,σFV为当量应力。
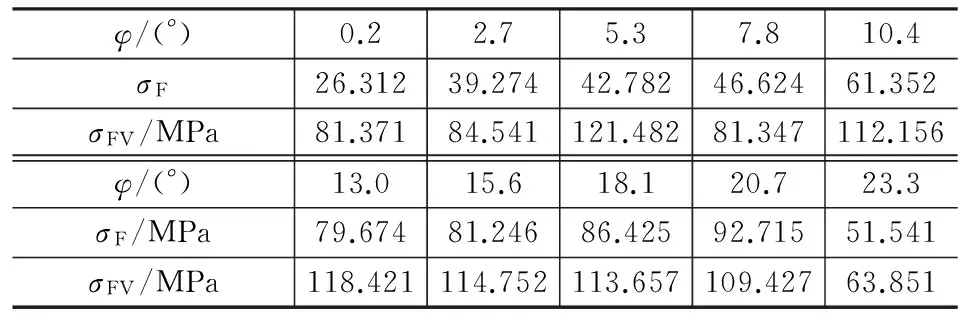
表2 圆柱齿轮齿根当量应力及弯曲应力计算结果
2.2 实际应用
由于空间站需实现推进剂的在轨补加,故需要补加系统,而补加系统中压气机是一关键单机,压气机能否可靠工作是补加过程能否成功实现的关键之一。电机组件作为压气机装置的动力源,实现压气机的启动、运转和停机。图6为我们提供给用户的电机组件产品。

图6 压气机用电机组件
由于用户初期的技术指标提供错误,导致实际输出力矩比计算值超出了4倍,最终产品在寿命试验过程中出现太阳轮受力过大损坏现象。如图7所示,损坏的齿都是在齿根位置断裂,跟我们用软件模拟的效果一样。

图7 损坏太阳轮
3 结 语
由上面计算结果及应用实例总结出下面几点:
1) 由于圆柱齿轮的齿面轮廓在过度曲线处齿厚最小,导致啮合过程中的最大弯曲应力均出现在齿根位置;
2) 受齿形齿廓和载荷分配系数的影响,最大弯曲应力并不是单调递增,而是呈抛物线分布,在近齿顶处齿根弯曲应力出现峰值;
3) 以当量应力和弯曲应力的差值作为分析对象,可以发现随着啮合域从齿顶到齿根变化,其差值越来越大,这是弯曲应力逐渐变小的结果;
4) 以弯曲应力较大点的覆盖范围作为分析对象,可以发现随着啮合区域从齿顶到齿根逐渐变化,覆盖区域逐渐变小,于此同时该区域随齿啮合域方向呈非对称分布。
[1] 胡仁喜.ANSYS 8.2机械设计高级应用实例[M].北京:机械工业出版社,2005.
[2] 李特文.齿轮啮合原理[M].上海:上海科学技术出版社,1984.
[3] 方宗德.齿轮承载接触分析的模型和方法[J].机械传动,1998(2):1-3.
Bending Stress Analysis of Cylindrical Gear Based on Hertz′s Contact Theory
WANGHong-xiang,XIONGLin-gen
(No.21 Research Institute of CETC,Shanghai 200233,China)
The contact regions and the contact force distribution of the pinion were calculated based on the theory of point contact Hertz. The solid model of the pinion was built using Pro/E, the contact regions was simulated based on Hertz theory and the distribution of bending stress was calculated using ANSYS.
contact characteristic; finite element analysis; cylindrical gear; bending stress
2015-12-20
TH132.41
A
1004-7018(2016)06-0041-03

