基于突变理论的房地产财务指标评价

吴 媛，邓晓盈，辛 琳

（昆明理工大学，云南 昆明 650500）

基于突变理论的房地产财务指标评价

吴 媛，邓晓盈，辛 琳

（昆明理工大学，云南 昆明 650500）

近年来，我国房地产行业受宏观经济影响，净利润出现下滑趋势或者严重亏损，房地产行业种种风险及监管不足、信用缺失等问题被暴露出来，直接影响到我国银行坏账准备率。房地产行业的信用缺失和信用体系不完善，已严重影响该行业的健康发展。文章根据突变理论原理，借助于分层方法应用在该理论的指标选取原则上，减少主观性，以30家上市房地产企业的财务数据为依据，通过突变理论原理度量企业的财务风险状况。

突变理论；财务指标；控制变量；房地产企业

［DOI］10.13939／j.cnki.zgsc.2016.46.016

1 引 言

我国房地产行业是整个经济建设的重要部分，其上、下游产业牵连甚广，城市发展和经济结构基本格局的主要动力都来自于房地产，当前国内二、三线城市正面临着去库存的压力，而一线城市房价大起大落，多个城市出台不同力度的调控约束政策，限制楼市过热上涨，而引发泡沫经济，同时我国房地产行业种种风险及监管不足、信用缺失等问题也被暴露出来，其中房地产泡沫经济直接影响到我国银行坏账率的提高，已成为现阶段的两大经济危机，房地产行业的信用缺失和信用体系不完善，已严重影响该行业的健康发展和我国经济。

房地产财务安全性直接关系到企业的生死存亡，间接影响到投资者和债权人的利益，对房地产行业财务指标，客观、高效的评价方法是信用管理体系对数据处理、分析的核心问题之一。然而传统的信用评级方法主观性过强，对指标的权重问题带有人为性，导致评级结果因人而异，与实际结果评价存在差异，而且培养一个专业、综合的高级信用管理师成本过大，国际上，随着信用风险越来越复杂，传统的信用评级方法渐渐地不再适应现代管理。

现代风险管理是以信用数据为基础，以计算机技术为平台，运用数据库、数据挖掘和数学模型等金融工具和梳理统计方法，对企业违约可能性进行量化，并通过计算机系统对评级对象业务进行监控的一种有效管理方式。本文在建立房地产行业信用评级的体系下通过突变理论模型对该行业的财务指标进行评价，将分层方法引用进来辅助该评级方法，从而减少主观影响，客观公正地评估一个企业，也提高第三方评级机构的工作效率。

2 突变理论的基本原理

2.1 突变理论

突变理论是一种新的数学方法，主要以不连续、奇点为研究方向，在1972年，比利时数学家托姆（R.Thom）用法文发表的《结构稳定性与形态发生学》首先提出。［1］［2］在现代分析数学研究的基础上，通过对集合、拓扑、微分几何、群论、流行等数学方法的综合，发展了突变理论。突变理论有两种表达形式：一种形式是通过用现代分析数学的形式表达出来的，我们称之为高等突变理论；另一种形式是以古典分析数学作为该理论的辅助条件，通过现代分析数学思想方法表达出来，称之为基本突变理论。［3］由于高等突变理论过于高深，一般学者对其研究过少或者难以掌握，在解决一般应用问题上，基本突变理论已经足够了，因此现在大多数研究的都是后者。

2.2 突变理论的应用发展

现在突变理论正在被诸多学者研究并运用在其他学科当中，其发展前景存在一定的空间，前景十分深广。当前，众多学者通过对突变理论的研究和应用，在自己的学科上已经得到了一定的成果。沈细中、沈华中、赵寿刚、冯厦庭在《大坝突变理论安全评价模型》中以突变理论为基础，通过围堰水位、温度及时间的影响因素，建立了大坝尖点安全评价模型。［4］龙琼、胡列格、张谨帆、周昭明在《基于尖点突变理论模型的交通事故检测》中利用尖点突变理论，计算出交通实际工况的速度、流量之间的数值关系，为城市道路交通流表征建立了模型。［5］范留明、耿鹏超在《突变理论在边坡工程应用的研究进展》中结合目前建设工程存在的问题，探讨突变理论在边坡工程的发展趋势。［6］英国的S.I Pratt借助于突变理论原理，在设计计算机操作系统时，查找系统数据一般丢失的原因。［7］

2.3 突变理论的基本模型

突变理论可谓是奇点、分歧方法的智囊，现在在探索复杂性的问题上突变理论已成为不可或缺的解决方法［3］。在突变理论的基础上，对于奇点和分歧在任何维空间当中无论系统演化多么复杂，都可以用数学形式精确地表述，这样对于复杂多变的奇点和不连续的问题就变得简单了。［8］［9］［10］当突变理论的控制量个数n（n≤4）时，突变结构有7种基本类型（见表1），分别为折迭突变（Fold Catastrophe）、尖点突变（Cusp Catastrophe）、燕尾突变（Swallowtail Catastroph）、蝴蝶突变（Butterfly Catastrophe）、双曲脐点（Hyperbolic Umbilic）、椭圆脐点（Elliptic Umbilic）和抛物脐点（Parabolic Umbilic）。系统微分方程一般都存在未知的条件，依据突变理论原理，系统中其他的定性或定量状态可以用已知的控制变量预测。

在模型中f（x）表示状态变量X的势函数，而a、b、c、d是模型中的控制变量.根据突变理论，平衡曲面是势函数f（x）的所有临界点构成的，其方程为f′（x）＝0.它的奇点集为f″（x）＝0，对势函数进行X的消元，突变系数的分歧点集方程就被求出.当控制变量a、b、c、d满足分歧点集方程关系时，系统的突变将会发生。

根据上述原理最终得到：

折迭突变模型：xa＝

尖点突变模型：xa＝，xb＝

燕尾突变模型：xa＝，xb＝，xc＝

蝴蝶突变模型：xa＝，xb＝，xc＝，xd＝

2.4 突变理论对数据和指标选取的原则

2.4.1 底层指标的原始数据应更改为(0，1)的数值，数值越大越好

利用突变理论作为信用风险评价模型，按照突变级数法的要求，控制变量必须取得(0，1)数值作为参考，数值的绝对值越大越符合要求.所以对原始数据要加以修正，本文利用直线型无量，钢化法变换法修正公式为：

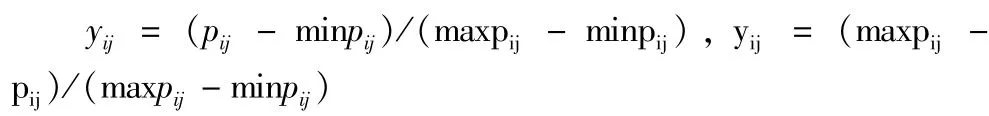
yij为第j个评级对象下的第i个指标控制变量值，pij为第j个评级对象下的第i个指标值。前者为正向指标选取公式，指标越大越好，后者为逆向指标选取公式，在指标当中只有资产负债率为逆向指标，越小越优，其他指标均为正向。

2.4.2 判断财务指标中的各个变量的重要程度

在此模型当中信用风险状况用X表示，状态变量a、b、c、d为信用风险模型中的财务指标控制变量，控制变量最终的量变结果是信用风险的质变，模型中控制变量在变化时，对状态变量改变具有不同的效果，我们要对控制变量的重要程度进行判断，一般模型当中变量的重要程度a＞b＞c＞d。因此在进行信用风险度量时，应确定在模型当中指标的重要程度。

2.4.3 变量间的“互补”和“非互补”

在同一指标下的控制变量，它们之间的关系一般存在着“互补”和“非互补”的关系，对于控制变量是“互补”关系的，可以彼此弥补自身的缺陷，此时状态变量可以取各控制变量对应状态变量的平均值；“非互补”关系的控制变量彼此之间既不能替代也不能弥补彼此的不足，在控制变量当中把最小值的变量称为“瓶颈”，要选则状态变量为与之对应称为“瓶颈”的控制变量，作为所需的状态变量值。［11］在实际工作中，往往有这样的情况，目标之间的互补关系要在各目标达到一定的限值之后才能互补，达不到限值则不能互补，限值规定为多大，这取决于实际评价条件的要求，它由评价决策者根据实际情况决定。［12］

3 分层法对指标进行分析，判断指标之间的重要程度

第三方信用评级机构对一个企业进行分析评价是从财务和非财务角度评价的，可见财务分析在一个企业的信用评级上具有显著的地位，本文主要分析的是房地产企业的财务指标，选取企业的财务指标原则是从企业的偿债能力、盈利能力、经营能力、资本能力四个方面评价一个企业资金的收益性、安全性和企业的成长性，并结合上市房地产企业在各大网站上公布的的财务报表数据进行分析。

利用层次分析法对房地产企业财务指标进行分析，首先确定层次结构，本文层次结构主要分为以“房地产企业信用评级财务指标”为首层、主要财务指标分析层（盈利能力，经营能力，偿债能力，资本实力）、主要财务指标分解层（四大能力指标以下的财务指标）。假设以上层元素B为准则，所支配的下层元素为C，令A＝（aij）n×n表示两两比较判断矩阵，aij表示元素Ci和Cj相对于B的重要性标准，此标准度的含义如表2所示。［13］判断矩阵A具有如下性质aij＞0，aij≥，aij＝1。

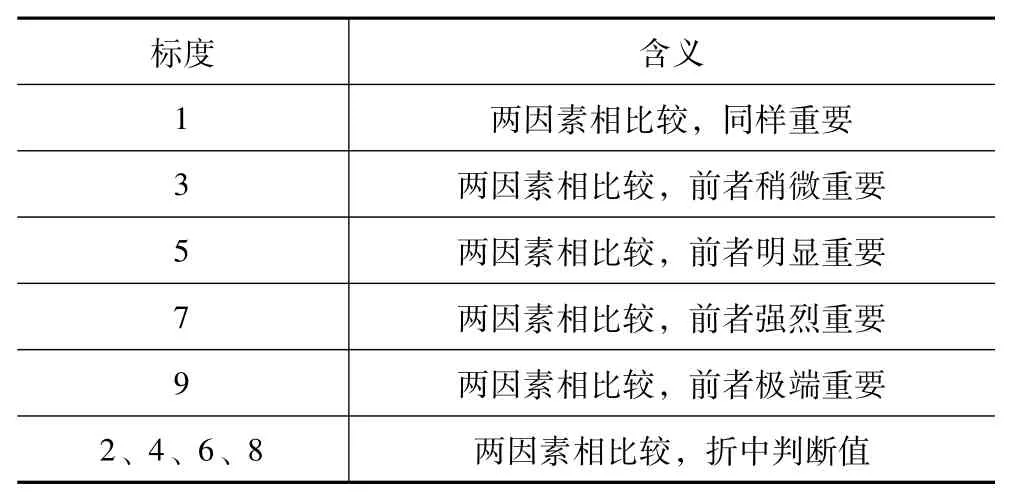
表1 1-9标度的含义

第一，A中每行元素连乘并开n次方，ω°i＝， i＝1，2，…，m；

第四，求λmax值。

由表1标度表判断的标准，我们可以比较房地产企业的信用评价财务指标的相对重要性，通过比较我们得到下列关于盈利能力、偿债能力、营运能力、资本实力的比较数据。

解：计算A中每一行的乘积为m1，m2，m3，m4

求m1，m2，m3，m4得四次方根n＝()4

w1＝＝2.59，

w2＝1.189，w3＝0.841，w4＝0.386

上述判断矩阵得到盈利能力、偿债能力、营运能力、资本实力的权重值为w1＝（0.5，0.25，0.15，0.1）。（考虑到实际生产当中，计算不宜太复杂，取值综合了此方法和实际情况的考虑）

矩阵C1和C2、C3分别为盈利能力、偿债能力、营运能力中的指标比较数据。

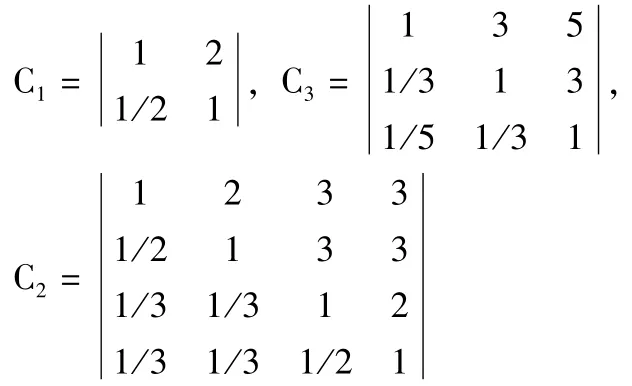
同理得到盈利能力中的净利润率和总资产报酬率的权重值w2＝（0.55，0.45）。

偿债能力中的流动比率、速冻比率、总资产负债比率、应收账款周转率的权重值w3＝（0.45，0.3，0.15，0.1）。

营运能力中的存货周转率、固定资产周转率、总资产周转率的权重值w4＝（0.6，0.3，0.1）。

4 模型应用

本文选取30家上市房地产公司财务数据作为参考，数据在Excel中进行处理。万科、保力地产、华夏幸福、金地集团、金隅股份、金科股份、金融街、宝安地产、中粮地产、中航地产、中南建设、滨江集团、华侨城A、北辰实业、京投银泰、荣盛发展、信达地产、迪马股份、首开股份、宁波富达、格力地产、云南城投、华业地产、中弘股份、南京高科、嘉凯城、福星股份、新华联、冠城大通、华远地产30家开发商的财务综合能力分别见表2。

表2 数 据

通过以上数据最终得到上市房地产企业财务的风险程度状况见表3。

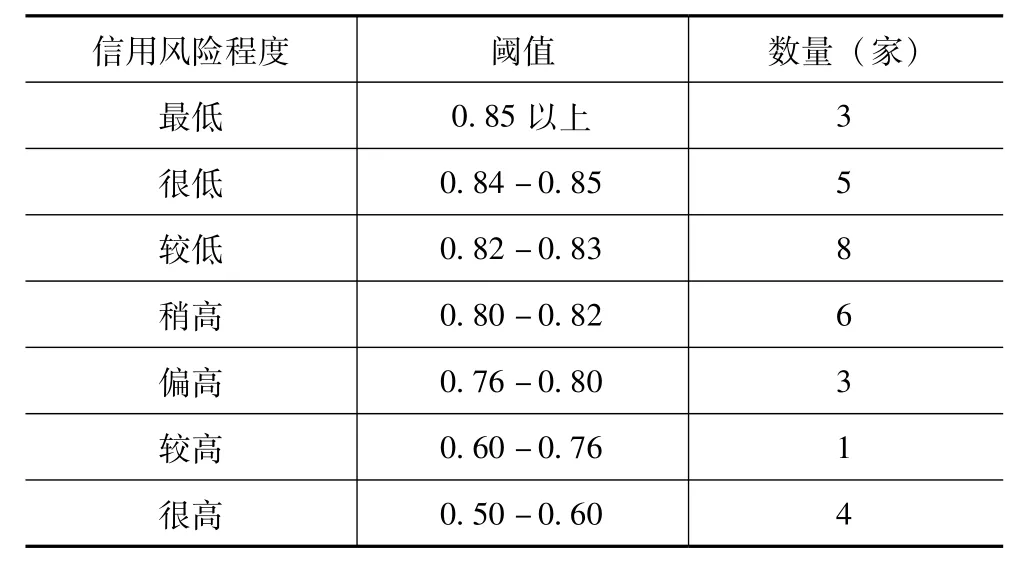
表3 信用风险程度及阈值

5 结 论

本文以突变理论和模糊数学方法结合，构建上市房地产企业财务风险模型，利用模型对30家上市房地产企业的财务数据进行归一计算，得到了各个指标隶属的函数值，利用这个数值得到了上市房地产企业的财务综合能力的高低，同时度量了其信用风险程度状况，旨在说明该模型在信用评级中的适用性，模型中对各个指标的重要性判断，使用了模糊数学当中的分层方法，减少了主观性，客观公正地评级一个企业，评估结果更接近于实际，此方法比一般方法更适用于第三方信用评级机构使用，提高公司的工作效率。

利用突变理论模型仅仅是对上市房地产公司的财务指标进行风险度量，并没有考虑到行业的其他因素和宏观环境对上市房地产公司信用评级影响，因此在这里不能完全对企业进行评级。另外，样本上仅仅对30家公司进行比较，在选择每个财务上的指标最大值和最小值是根据30家企业的数据比较和专家意见确定下来的，可能存在偏差，但本文意在给房地产企业信用风险度量提供一个度量方法，在实践操作上应选择数据越多越好，减少偏差，对评级出来的结果更加精准。本文是利用上市房地产企业的财务数据进行对普遍房地产公司的研究，所以并没有全面考虑上市房地产的财务数据。

［1］Poston T，Ian Stewart.Catastrophe Theory and Its Application ［M］.Lord：Pitman，1978：172-191.

［2］Zeckhauser Richard.The Economics of Catastrophes［J］. Journal of Risk and Uncertainty，1996（2）：101-105.

［3］R.吉尔莫雷.科学与工程中的基本突变理论［M］.成都：西南交通大学出版社，1988.

［4］沈细中，沈华中，赵寿刚，等.大坝突变理论安全评价模型［A］.大坝安全与堤坝隐患探测国际学术研讨会论文集，2005.

［5］龙琼，胡列格，张谨帆，等.基于尖点突变理论模型的交通事故检测［J］.土木工程学报，2015（9）：112-116.

［6］范留明，耿鹏超.突变理论在边坡工程应用的研究进展［J］.地球科学进展，2015（11）：1268-1277.

［7］Ho Thomas，Anthony Saunders.A Catastrophe Model of Bank Failure［J］.Journal of Finance，1980（35）：1189-1207.

［8］S Henley.Catastrophe Theory Models in Geology［J］.Journal of the International Association for Mathematical Geology，1976，8（6）：133-144.

［9］K T Sundara Raja Iyengar，K Chandrashekhara，V K Sebastian.On the Analysis of Thick Rectangular Plates［J］.Archive of Applied Mechanics，1974，43（5）：160-165.

［10］Alberto Carpinteri.A Catastrophe Theory Approach to Fracture Mechanics［J］.International Journal of fracture，1990，44（1）：88-94.

［11］叶蜀君.信用风险的博弈分析与度量模型［M］.北京：中国经济出版社，2008：210.

［12］朱顺泉.企业资信评级创新方法及应用［M］.成都：西南财经大学出版社，2002：135-136.

［13］张所地，吉迎东，胡琳娜.管理决策理论、技术与方法［M］.北京：清华大学出版社，2013：261-264.

本文系国家创新基金资助项目（项目编号：140516153446035）。

吴媛（1986—），女，河北秦皇岛人，昆明理工大学研究生。研究方向：房地产信用评级；通讯作者：邓晓盈（1962—），女，广州梅州人，昆明理工大学建筑工程学院副教授，硕士生导师。研究方向：房地产技术经济和市场经济，企业信用评级；辛琳（1993—），山东潍坊人。研究方向：房地产经济学。