基于滑模控制的小型风电并网MPPT控制研究
吴少石,解 恩,曾 世,刘惠婷
(西北工业大学,西安 710129)
基于滑模控制的小型风电并网MPPT控制研究
吴少石,解 恩,曾 世,刘惠婷
(西北工业大学,西安 710129)
针对小型单相风力发电并网系统(发电机额定功率1 kW),基于滑模控制的强鲁棒性和快速响应特性,设计了一种滑模MPPT控制算法,并做了优化。该并网系统由MPPT控制算法直接给定并网电流有效值,并捕捉电网电压波形来共同确定系统给定的并网电流参考值,以此来实现并网系统的MPPT控制要求。通过MATLAB/Simulink仿真软件对该系统控制方案进行仿真分析,仿真结果说明所设计的滑模MPPT控制算法能够使得整个并网系统快速有效地跟踪最大功率点以及实现并网时功率因数等于1;优化后的方案能够一定程度削弱系统在稳态运行时的抖振以及并网电流波形畸变的问题。
风力发电;并网;最大功率点追踪;滑模控制
0 引 言
随着工业的发展和全球爆发的石油危机,环境和能源问题已成为困扰人类发展的两大难题,很多国家面临能源短缺的困境,风电作为现阶段最具规模化开发和市场化利用条件的非水可再生能源,作为清洁环保的新能源,是未来电力能源发展的趋势。而能够使用大型风电系统的地区对风速要求高,局限性较大。现存的小型风电系统多为离网型,需采用蓄电池,成本高、电能不稳定。因此研究低成本、高效率的小型风电并网系统有着十分重要的意义[1]。
目前,风力发电常用的最大功率点追踪(以下简称MPPT)控制方法与光伏发电类似,有恒定电压法、增量导纳法和扰动观测法三种[2],这些方法虽然能够跟踪最大功率点,但是由于控制算法自身造成的扰动等原因,会对系统的效率和运行稳定性造成不良的影响。而滑模控制(以下简称SMC)能够克服系统的不确定性,具有较快的响应速度,对干扰和未建模动态具有较强的鲁棒性[3]。基于文献[4],针对单相风力发电并网系统,提出一种基于滑模的MPPT控制算法,由MPPT控制算法直接给定并网电流有效值。鉴于文献[5-8]中饱和函数替代符号函数的优化方法在电机SMC中的控制效果较好的特性,将该方法用于本文风电并网逆变器的滑模MPPT的优化控制中。
本文所实现的风力发电并网MPPT是基于LCL滤波的单相电压源型逆变器,通过控制并网电流来控制逆变器。下面首先简要介绍了基于滑模MPPT并网系统控制方案原理。然后给出整个风力发电系统的拓扑和控制结构图,并根据风力发电最大功率点追踪的原理和条件,针对使用额定功率1 kW的永磁同步发电机的小型单相风力发电并网系统,设计滑模MPPT控制算法。最后用MATLAB/Simulink仿真软件对该风力发电并网系统控制方案进行仿真分析,仿真结果说明所设计的滑模MPPT并网控制方案快速有效,使整个并网系统能够快速地跟踪风力发电的最大功率点,并实现系统输出的功率因数等于1;优化后的方案能够一定幅度地削弱系统在稳态运行时的抖振以及并网电流波形畸变的问题。
1 基于SMC的并网系统MPPT控制方案
使用基于SMC的MPPT算法计算并网电流参考有效值,实质是重新构造一个系统,选取一个滑模平面,通过不断修正控制所需的系统输出量的值来校正整个系统运行状态,同时通过开关函数的切换,不断的改变系统结构,使得系统状态点在滑模平面附近作小幅度的运动,最终达到稳态[9]。
本文以小型的单相风力发电并网系统模型为基础,设计滑模MPPT控制算法,通过最大功率点处的功率电压曲线斜率为0的特点来确定滑模平面,经过等效控制的控制函数的切换,使系统稳定运行在最大功率点处。该MPPT滑模控制算法给定并网电流有效值,与捕捉的电网电压波形来共同确定并网电流参考值,并以此控制逆变器来实现并网系统的控制。
2 单相风力发电并网系统模型
本文所研究的是基于LCL滤波的小型风力发电并网系统,电路拓扑及其控制结构如图1所示。该系统主电路主要包括风力机、发电机、整流桥,DC-DC升压电路、单相逆变桥、LCL滤波电路和电网。此次控制主要是来控制逆变器来实现最大功率点并网,DC-DC升压电路的主要作用是用来稳定逆变器的输入电压,以防逆变器前级输入电压低于后级电网电压,从而造成电流倒灌的现象[10]。为了简化系统模型,此次仿真中去掉了DC-DC升压电路,使用一个二极管来防止电流倒灌。

图1 风电并网系统逆变器电路拓扑及其控制结构图
在该系统中,为了实现MPPT算法设计,需要测量的量有逆变器前级的输出电压Udc,输出电流Idc,并网电流有效值Io和电网电压的有效值Ug以及实时相位。在该结构图中,电容C1的作用是直流侧滤波以及稳压。滤波电容C2的作用主要是衰减高次电流谐波,与L1,L2共同组成并网系统的LCL滤波器。
3 基于SMC的MPPT算法设计
风力机输出功率随着风速大小的不同而变化。当风速改变时,风力机的转速也在改变,所以在各风速下对应存在一个最佳转速,能使风力机运行在最大功率曲线上。在桨距角α一定时,不同风速下风力机输出功率与转速的关系曲线如图2所示。
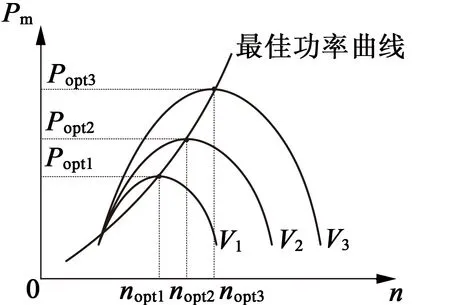
图2 桨距角α不变时风力机特性曲线
随着风速的变化,其输出功率变化相当大,但在一定风速下,其输出功率与风机转速曲线只有一个最大功率点[11],也就使得在一定风速下,风力发电机输出功率与电压曲线也只有一个最大功率点。由于此次设计仿真没有添加DC-DC升压电路,所以逆变桥前级的输出功率与输出电压曲线也只有一个最大功率点,该P-U曲线如图3所示。

图3 P-U曲线
本文所提出的MPPT控制方法是基于滑模控制,根据以上已知原理和条件来设计单相风力发电并网系统的滑模MPPT控制算法。
3.1 状态方程的建立
理想状态下逆变器输入前后功率可以视为相同,则有:
(1)
式中:i1是逆变桥直流侧输入电流;Ug为电网电压有效值;Io为并网电流有效值。
由此可得逆变器输入电流:
(2)
系统直流侧状态方程:
(3)
将i1表达式(2)带入式(3)可得:
(4)

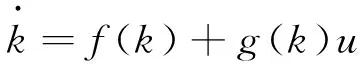
(5)
3.2 定义滑模切换面
已知图3的P-U曲线,根据最大功率点处曲线斜率为0,可以定义切换面为:
(6)
式中:k为Udc,P为逆变桥前级的输出功率,P=UdcIdc。
3.3 等价控制
此处采取等价控制的方式:
(7)
根据滑动动力学,有:
(8)
将式(5)代入式(8)可得:
(9)
(10)
3.4 滑模切换面可达性证明
(11)
其中,李雅普诺夫函数V>0。
李雅普诺夫函数的导函数:

(12)
(13)
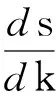
综上所述,可得单相风力发电并网系统MPPT的滑模控制律:
(14)
3.5 MPPT算法优化
由SMC理论可知,被控系统到达稳定状态后,由于控制方式的影响,不可能理想的在滑模切换面上运行,其实际的稳定状态是系统状态点在滑模切换面附近作小幅度地穿越滑模切换面的运动,这就是滑模控制系统运行的抖振问题。虽然该问题是不可避免和完全消除的,但是可以通过一些方法来削弱抖振的幅度。在此,本次优化使用饱和函数f(s)代替符号函数sign(s)的方法,目的是在符号函数值跳变前增加一个缓冲段,并以此来削弱控制系统稳定状态运行时的抖振幅度。该饱和函数的表达式:
(15)
式中:k1为饱和函数斜率。 饱和函数f(s)图形如图4所示。
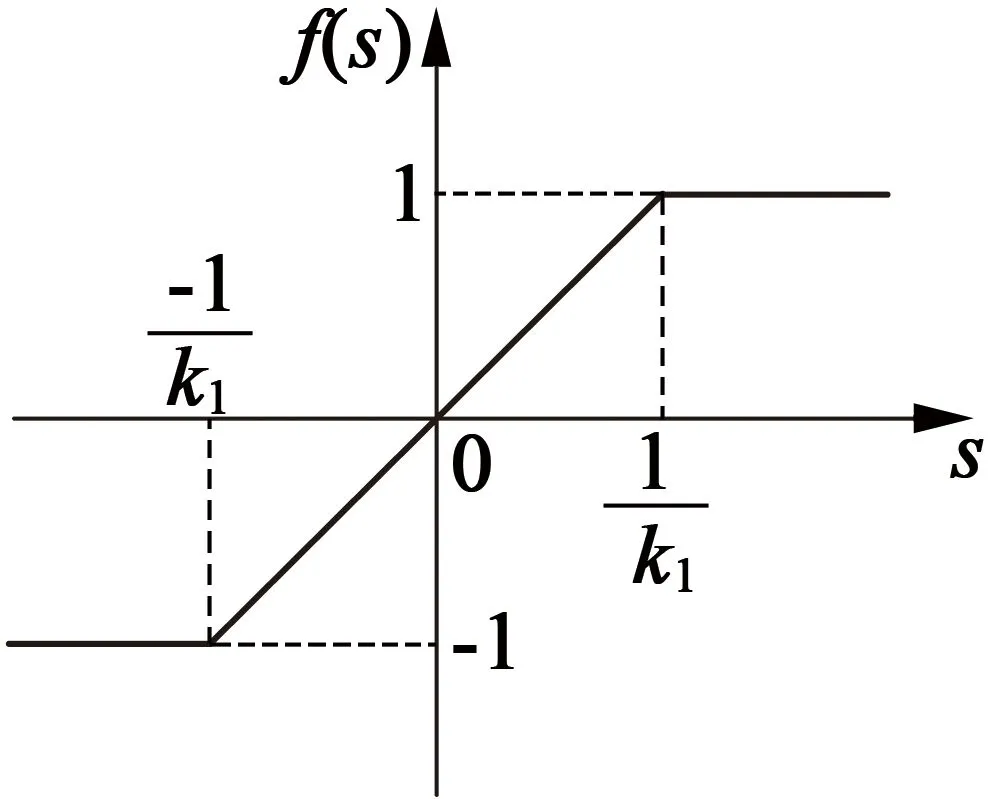
图4 饱和函数f(s)
综上,对于优化后的控制算法,切换面:
(16)
滑模控制律:
(17)
与优化前的方案滑模切换面可达性证明同理可以推导得到当uh≥0时系统渐进稳定,即切换面的可达,其余部分都与之前相同,此处不再赘述。
从后面系统测试后可知uh=1.25时,k1在1.5~2的范围内系统功率抖振波动的削弱幅度与并网电流的波形效果总体达到最优,因此取k1=1.7,uh=1.25。
4 MATLAB/Simulink仿真模型及结果分析
对于本次研究的小型风电并网系统,在MATLAB/Simulink条件下,其基于SMC的并网MPPT控制仿真模型如图5所示。由于风力机带动发电机输出电能的研究分析形式是功率和发电机转速的曲线关系,其曲线如图2所示,而经过研究,转换到逆变器前级时电能的研究分析形式是功率和电压的曲线关系,其曲线如图3所示。所以仿真模型中逆变器输入使用一个自建电源模块来模拟风力发电机的电能输出,即满足如图3所示曲线关系的直流电源。

图5 基于滑模的并网MPPT控制系统仿真模型
其中,根据优化前算法方案搭建的滑模MPPT模块如图6所示。根据优化后算法方案搭建的滑模MPPT模块如图7所示。

图6 优化前的滑模MPPT算法模块
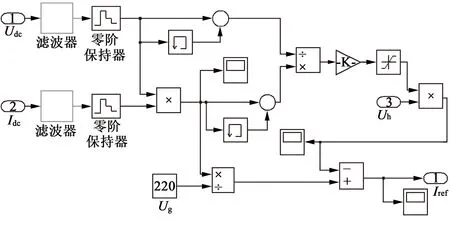
图7 优化后的滑模MPPT算法模块
在风速分别在0.25 s和0.7 s发生变化的情况下,使用并网系统模型在理想状态下实现MPPT以及并网运行的功率曲线以及并网电流与电网电压对比的波形曲线如图8所示。
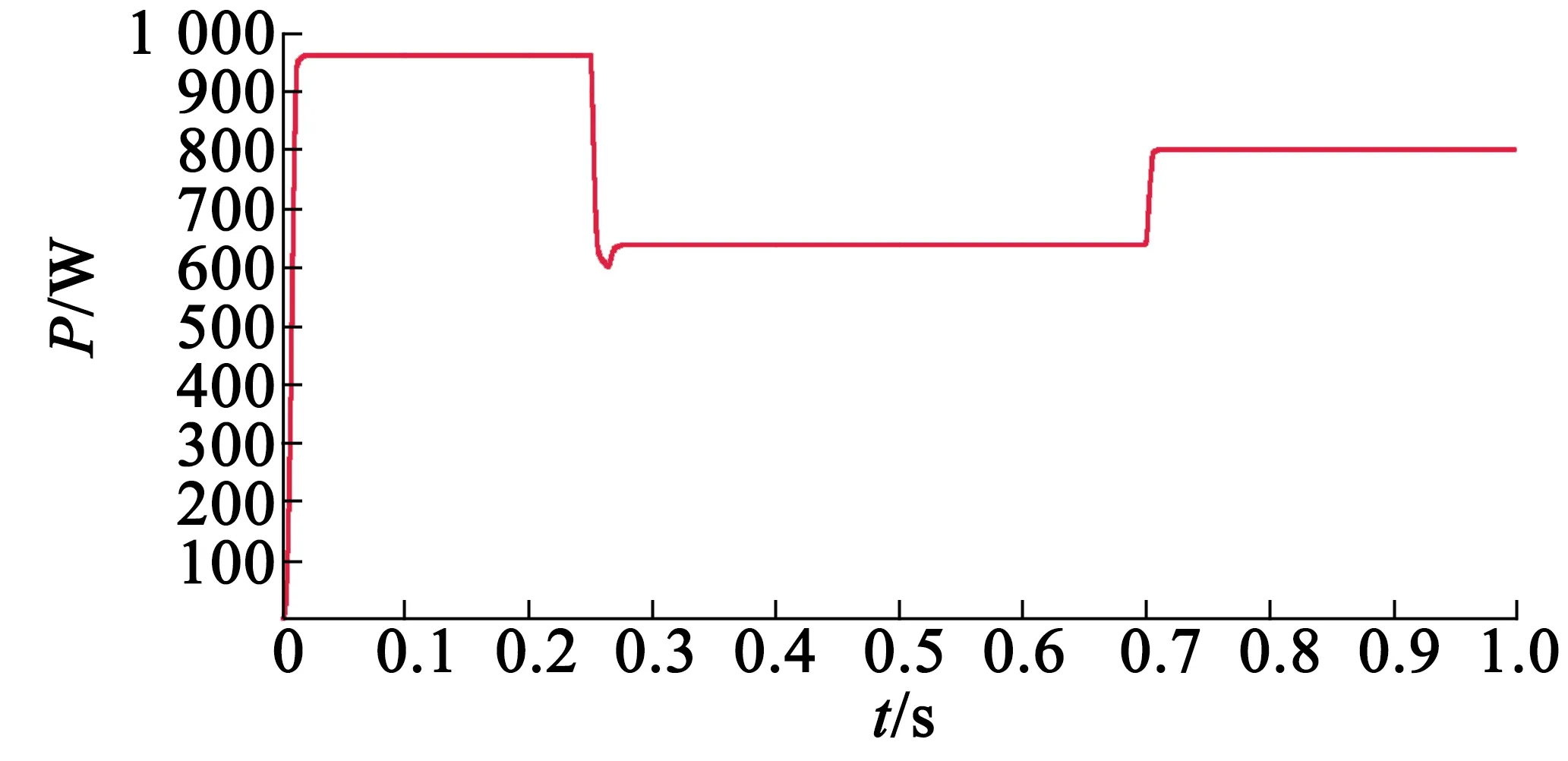
(a) 功率
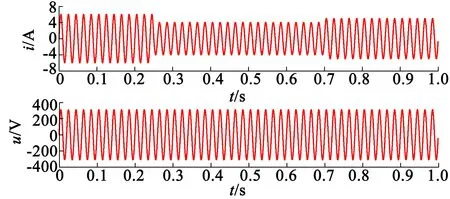
(b) 并网电流与电网电压对比
当使用优化前的滑模MPPT控制算法对该并网系统进行仿真,un取1.25,仿真时间为1 s,得到功率曲线以及并网电流和电网电压对比波形分别如图9所示。
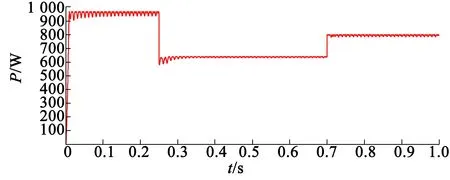
(a) 滑模MPPT控制算法的功率

(b) 滑模MPPT控制算法的并网电流与电网电压对比
当使用优化后的滑模MPPT控制算法对该并网系统的进行仿真,uh取1.25,仿真时间为1 s,饱和函数的斜率k1值分别为1,1.7和3时的功率曲线以及并网电流和电网电压对比波形分别如图10所示。
经过一系列仿真实验,uh=1.25时,k1在1.5~2的范围内系统抖振的削弱幅度与并网电流的波形

(a) k1=1时的功率曲线

(b) k1=1时的并网电流与电网电压对比波形

(c) k1=1.7时的功率曲线

(d) k1=1.7时并网电流与电网电压对比波形

(e) k1=3时的功率曲线

(f) k1=3时并网电流与电网电压对比波形
效果总体达到最优,并在这一系列的仿真结果中选择了以上状态时的结果曲线和波形。由以上仿真结果可知,uh=1.25时,在使用优化前的滑模MPPT控制算法的并网系统中,功率的波动为925~968.1,602.5~639.2,756~799.9,并网电流与电网电压基本同相,但波形畸变严重。相同uh值的情况下k1=1时,使用优化后的滑模MPPT控制算法的并网系统中,功率的波动为939.2~968.1,627.7~639.2,783.6~799.9,并网电流与电网电压基本同相,并且几乎没有畸变;在k1=1.7时,功率的波动为941.6~968.1,630.7~639.2,785.6~799.9,并网电流与电网电压基本同相,稍微开始有畸变;在k1=3时,功率的波动为942.4~968.1,631.9~639.2,786.4~799.9,并网电流与电网电压基本同相,波峰波谷处畸变相对于k1=1.7较大。由此可见,使用优化后的滑模MPPT控制算法能够有效地抑制功率的抖振波动以及并网电流畸变,并且在k1=1.7,uh=1.25时系统功率抖振波动的削弱幅度与并网电流的波形效果总体达到最优,因此选定优化后的滑模MPPT算法参数k1=1.7,uh=1.25。从以上功率曲线的仿真结果可知,在风速变化的条件下,优化前系统运行到稳定状态时的响应时间为0.325 s,0.023 s和0.025 s,优化后的响应时间为0.0325 s,0.015 s和0.020 s,可知优化后的响应时间更短,性能更好。
5 结 语
本文针对使用额定功率1 kW永磁同步发电机的小型单相风力发电并网系统,设计出了一种基于滑模的并网MPPT控制算法,并且用饱和函数替代符号函数的方法对算法进行了优化。并对该系统进行了仿真分析,仿真结果说明所设计采用的方案能够使得整个并网系统快速地跟踪风力发电系统的最大功率点以及实现并网时的功率因数等于1;优化后的方案能够一定幅度地削弱系统在稳态运行时的抖振以及并网电流波形畸变的问题,对小型单相风力发电并网系统有较强的应用价值。
[1] 李德孚.户用小型风力发电系统现状与发展(上)[J].节能与环保,2005(6):14-16.
[2] 李晶,窦伟,徐正国,等.光伏发电系统中最大功率点跟踪算法的研究[J].太阳能学报,2007,28(3):268-273.
[3] 田宏奇.滑模控制理论及其应用[M].武汉:武汉出版社,1995:1-20.
[4] 张云贵,薛向荣,佟为民,等.采用滑模变结构控制MPPT的三相光伏并网发电系统[J].电力自动化设备,2011,31(10):89-94.
[5] 鲁文其,胡育文,杜栩杨,等.永磁同步电机新型滑模观测器无传感器矢量控制调速系统[J].中国电机工程学报,2010,30(33):78-83.
[6] 鲁文其,胡育文,黄文新,等.无刷直流电机无位置传感器转子位置自检测复合方法[J].电工技术学报,2008,23(9):70-75.
[7] LU Wenqi,HU Yuwen,HUANG Wenxin,et al.Sensorless control of permanent magnet synchronous machine based on a novel sliding mode observer[C]//Vehicle Power and Propulsion Conference,2008.VPPC'08.IEEE,2008:1-4.
[8] LU Wenqi,HU Yuwen,HUANG Wenxin,et al.A hybrid approach of sensorless rotor position self-sensing for brushless DC Motor[C]//International Conference on. Electrical Machines and Systems,ICEMS 2008.IEEE,2008:1334-1337.
[9] 王丰晓.滑模变结构控制[M].北京:机械工业出版社,1995.
[10] 张啸.单相太阳能并网逆变器的研究与设计[D].济南:山东大学,2012.
[11] 彭国平,李帅,鱼振民,等.小型风电系统最大功率跟踪的研究[J].西安交通大学学报,2004,38(4):357-360.
[12] 刘金琨.滑模变结构控制MATLAB仿真[M].北京:清华大学出版社,2005:1-8.
Research of MPPT Based on Sliding Mode Control of Small-Sized Wind Power Grid-Connected System
WUShao-shi,XIEEn,ZENGShi,LIUHui-ting
(Northwestern Polytechnical University,Xi'an 710129,China)
Based on the strong robustness and fast response of sliding mode control, a sliding mode MPPT control algorithm for small-sized wind power grid-connected system (nominal power of the generator is 1 kW) was designed, then optimized. To realize MPPT control requirement in this grid-connected system, the virtual value of grid-connected current was given by MPPT control algorithm, and with the captured waveform of network voltage, those two determined the given grid-connected current reference value of system. Through analyzing the control scheme of grid-connected system with MATLAB/Simulink, the simulation results indicat that the designed sliding mode MPPT control algorithm can make whole system track the maximum power point rapidly and effectively, and the power factor is 1 when paralleling in the grid. Moreover, it can weaken the problem of buffet when operating in steady state and waveform distortion of grid-connected current in a certain extent after being optimized.
wind power generation; grid-connected; maximum power point tracking (MPPT); sliding mode control
2015-10-03
TM315
A
1004-7018(2016)08-0117-05
吴少石(1991-),男,硕士研究生,研究方向为电力电子与电力传动。

