混合动力汽车用内置永磁同步电动机参数估计方法研究

马建伟，梁晓琳，张鹏飞

(邢台职业技术学院，邢台 054000)



混合动力汽车用内置永磁同步电动机参数估计方法研究

马建伟，梁晓琳，张鹏飞

(邢台职业技术学院，邢台 054000)

内置式永磁同步电机具有恒功率范围宽、功率密度大、效率高等特点，因此其在混合动力汽车中的应用比较广泛。由于混合动力汽车用电机工作环境恶劣、负载突变大，且内置式永磁同步电机的参数易受温度、磁饱和等因素的影响，大大降低了其控制性能。针对电机的精确控制，首先建立了前置永磁同步电机的数学模型；电机转矩主要与磁链和d，q轴电感差值有关，故针对电机磁链和电感进行在线估计。提出了一种基于前馈式电流解耦的磁链估计算法，能够很好地消除工况变化对电机的影响；同时提出了一种基于功率闭环的d，q轴电感差值估计算法，可实现电机的精确控制。仿真和实验验证了所述参数估计方法的有效性。

内置永磁同步电机；磁链估计；混合动力汽车

0 引 言

当前汽车技术发展的主要方向在于新能源的利用，即新能源汽车。作为新能源汽车的主要形式，混合动力汽车的发展十分迅速。为保证混合动力汽车整车性能，驱动电机应具有高效、快速、准确和高可靠性等特点[1-5]。目前，混合动力汽车的驱动电机大多采用内置式永磁同步电动机(IPMSM)，实现电机的最优控制是保证整车性能的关键[6-7]。电机最优控制，主要在于两个方面：电机参数的实时估计和适应参数变化的控制算法，如此可以提高系统的鲁棒性。众所周知，电机参数随运行工况和环境会不停变化，例如永磁磁链、d，q轴电感等[8-9]。为解决此问题，国内外学者针对电机参数估计和相关控制算法展开了一些研究。

Morimoto S等人通过具体实验测量发现随着d，q轴电流的变化，d轴电感基本不会发生变化；而q轴电感会随着q轴电流的增大而减小；因此在控制过程中可认为d轴电感为常数并用线性方程描述q轴电感和电流之间的关系；但是并没有考虑d，q轴之间的交叉耦合效应，所以线性拟合是不够准确的[10]。

Qi G等人则考虑了交叉耦合效应，基于二维有限元法对d，q轴电感进行预测，并采用 MAP插值法对得到的d，q轴电感进行优化；但是该方法花费巨大而且无法满足所有工况，即在特殊工况下会出现较大偏差，无法实现最优控制[11]。

Boileau T等人分析了电机参数与电机稳态方程之间的关系，认为稳定工况下无法实现所有参数的识别，因此需要将部分参数假定为已知参数。另外，若要识别所有参数，需要采用信号注入等方法或增加传感器数量，上述方法并不适用于车用永磁同步电动机[12]。

哈尔滨工业大学郑维以及清华大学田硕等人将输出转矩实际值和参考值之间的关系制作成二维或三维表格(Map)，并存储在控制器内部，进而实现电机的精确控制。但是该方法存在一定的局限性：涉及参数较少，难以应对复杂的工况；涉及参数较多，会增加混合动力系统匹配的工作量[13-14]。

针对上述问题，本文建立永磁同步电机模型，提出参数的估计算法，并将参数估计与变参数控制算法相结合，通过仿真和实验证明了算法的有效性。

1 内置永磁同步电机数学模型

为便于分析和控制，可在d，q坐标系下，建立内置式永磁同步电动机电气数学模型，如图1所示。模型中绕组电阻rs可用于表示铜耗；铁耗电阻rc可用于表示铁耗；由于机械损耗与电气参数无关，另外杂散损耗难以在模型中具体表示，所以该模型不考虑机械损耗和杂散损耗。

图1 内置式永磁同步电机电气数学模型

根据图1中所示的内置式永磁同步电机电气数学模型，其电气方程可具体表示：

(1)

(2)

(3)

(4)

式中:vd和vq分别表示d轴和q轴相电压；rs为绕组电阻；id和iq分别表示d轴和q轴总电流；Lld和Llq分别表示d轴和q轴漏电感；Lmd和Lmq分别表示d轴和q轴磁化电感；icd和icq分别表示d轴和q轴铁耗电流；iod和ioq分别表示d轴和q轴总电流与铁耗电流的差值；Ld和Lq分别表示d轴和q轴总电感；ωe为电角速度；φf为永磁磁链；rc为铁耗电阻。

另外，永磁同步电机的转矩和机械方程可分别表示：

(5)

(6)

(7)

式中:Te为电机电磁转矩；p为电机极对数；Jm为转子转动惯量；TL为负载转矩；TMec为风阻和摩擦转矩；ωr为转子角速度；θr为转子位置。

若不考虑电流瞬态变化，那么稳态工况下的电机模型可描述：

(8)

(9)

(10)

(11)

(12)

电机铁耗可表示：

(13)

式中:φd和φq分别表示d轴和q轴磁链；Kh为电机磁滞损耗常数；Kf为电机涡流损耗常数；杂散损耗可表示：

(14)

式中:CStr为杂散损耗系数。机械损耗可表示：

(15)

式中:Bm为粘性摩擦系数；Tfric为摩擦转矩。

2 内置式永磁同步电机参数估计

由前文分析可知，内置式永磁同步电机参数较多，其中等效铁耗电阻、机械损耗系数、杂散电阻可通过测量获得。相对而言，电机的磁链和电感变化较大且建模比较困难；与d轴相比，q轴电感受磁饱和等因素的影响要明显。因此，本文以永磁磁链和q轴电感为例，进行在线估计。

2.1 磁链估计

由式(1)～式(4)可知，电机电压和电流相互耦合，为保证电流控制的精确性，需要对d，q轴解耦。基于电机数学模型，其电压传递函数可表示：

(16)

式(16)中最后一项为反向电动势，可通过解耦控制消除。具有前馈解耦功能的永磁同步电机电流环控制[15]如图2所示。

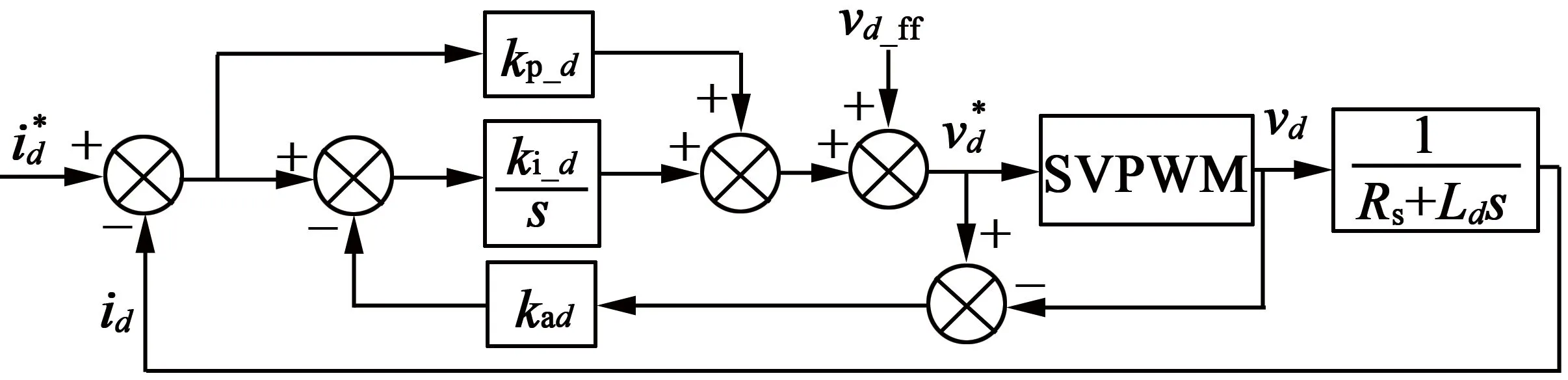
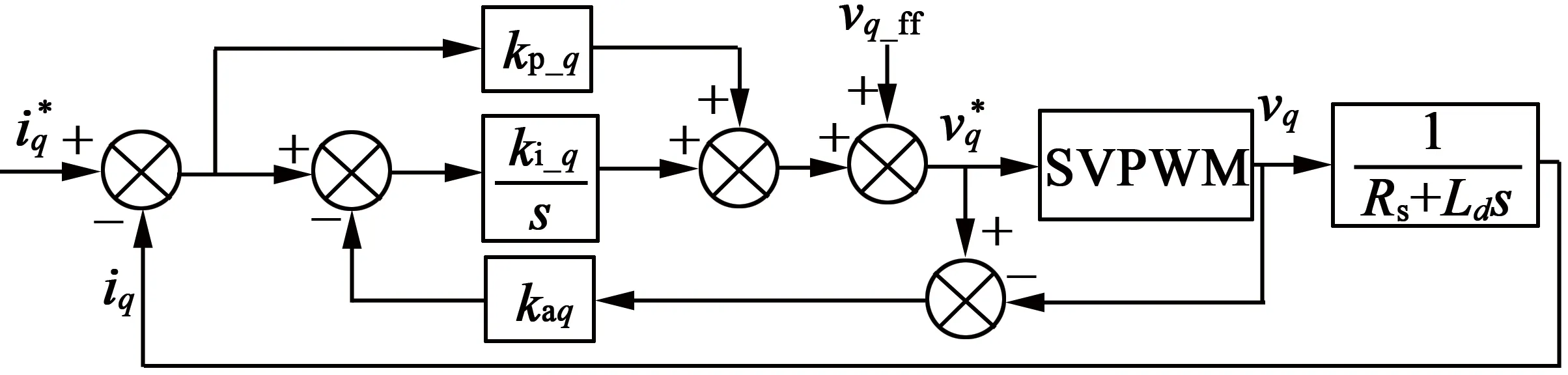
图2 前置永磁同步电机电流环控制框图

图2中的解耦控制电压可表示：

(17)

若PI电流控制器的输出值为vd_fb和vq_fb，则上述带前馈解耦电压补偿的电流环输出电压可表示：

(18)

在稳定工况下，电流环输出电流值能够较好地跟随参考电流值，因此可忽略式(16)中的微分项，由式(16)～式(18)可得：

(19)

由式(18)和式(19)可得：

(20)

由式(20)可知，PI电流控制器的输出值包括定子电阻压降和磁链估计误差。假设定子电阻的变化较小，可以忽略不计，那么可由电流环PI控制器的积分项得到磁链估计信息，即：

(21)

式中:vd_fb_i和vq_fb_i为电流环 PI 控制器的积分项；Δφd和Δφq为磁链误差，可表示成实际值和估计值之间的差值。

综上所述，前置永磁同步电机磁链估计算法可描述：

(22)

2.2 估计

(23)

此时参考转矩输出功率可表示：

(24)

在前述电流闭环控制下，实际输出电流id和iq可认为与参考电流相等，即：

(25)

另外，电机实际转矩功率：

(26)

假定交直轴电感实际差值为ΔL，交直轴电感理论差值为ΔL′。如果ΔL=ΔL′，则表示输出转矩实际值等于输出转矩参考值，转矩输出功率实际值等于转矩输出功率参考值；但是如果ΔL≠ΔL′，则表示输出转矩和转矩输出功率的实际值和参考值之间存在偏差。

将式(23)代入式(24)可得：

(27)

将式(27)对ΔL求偏导，可得：

(28)

一般情况下，混合动力车用电机可能处于电动机模式或发电机模式，即ioq数值可正或可负。鉴于内置式永磁同步电机的ΔL恒大于零，那么对(28)两边取绝对值，则有：

(29)

通过分析式(25)可知，ΔL偏差与功率偏差绝对值之间存在单调关系，所以ΔL的优化可以通过消除功率参考数值与功率实际输出数值之间的偏差来实现。在磁链估计和dL估计的基础上，基于最大转矩比电流算法，可以实现变参数的在线估计和控制，进而满足系统优化的需求，控制框图如图3所示。

图3 基于参数估计的变参数MTPA控制框图

3 仿真分析和实验验证

为验证上述参数估计方法的有效性，分别在额定工况(2000r/min,358N·m)和最大转矩工况(1 000 r/min,540 N·m)下，对本文所提出的磁链和ΔL估计算法进行仿真分析和实验验证。前置永磁同步电机相关参数如表1所示。

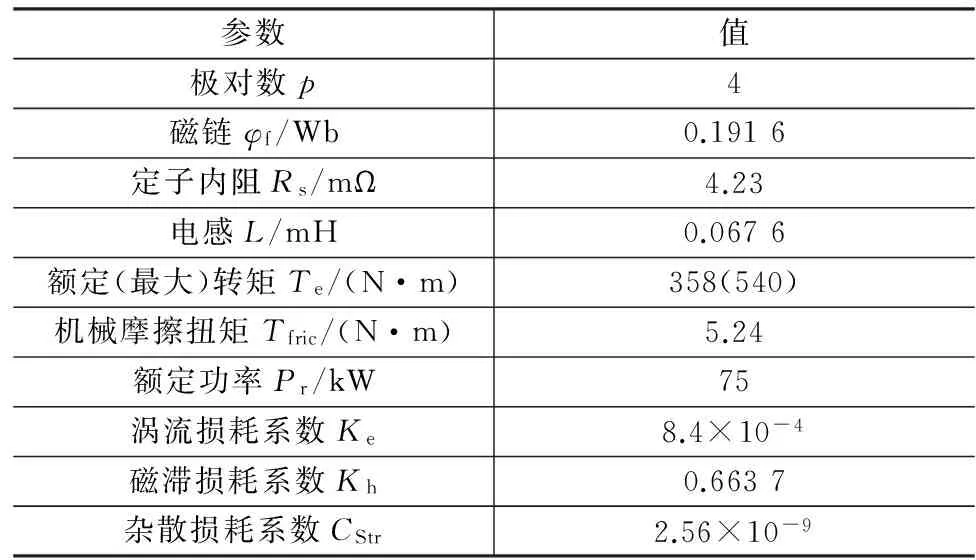
表1 内置永磁同步电机参数

3.1 仿真分析

根据图3所示的控制框图，在MATLAB/Simulink中建立对应的仿真模型进行仿真分析。仿真用参数设置如下： 估计器的工作频率为2 kHz；电流环PI控制器的频率为5 kHz；PWM 调制频率为10 kHz；电源选用288 V的直流电压源；忽略死区效应和电源内阻。仿真结果如图4和图5所示。

图4 额定工况(2 000 r/min，358 N·m)下磁链和dL估计

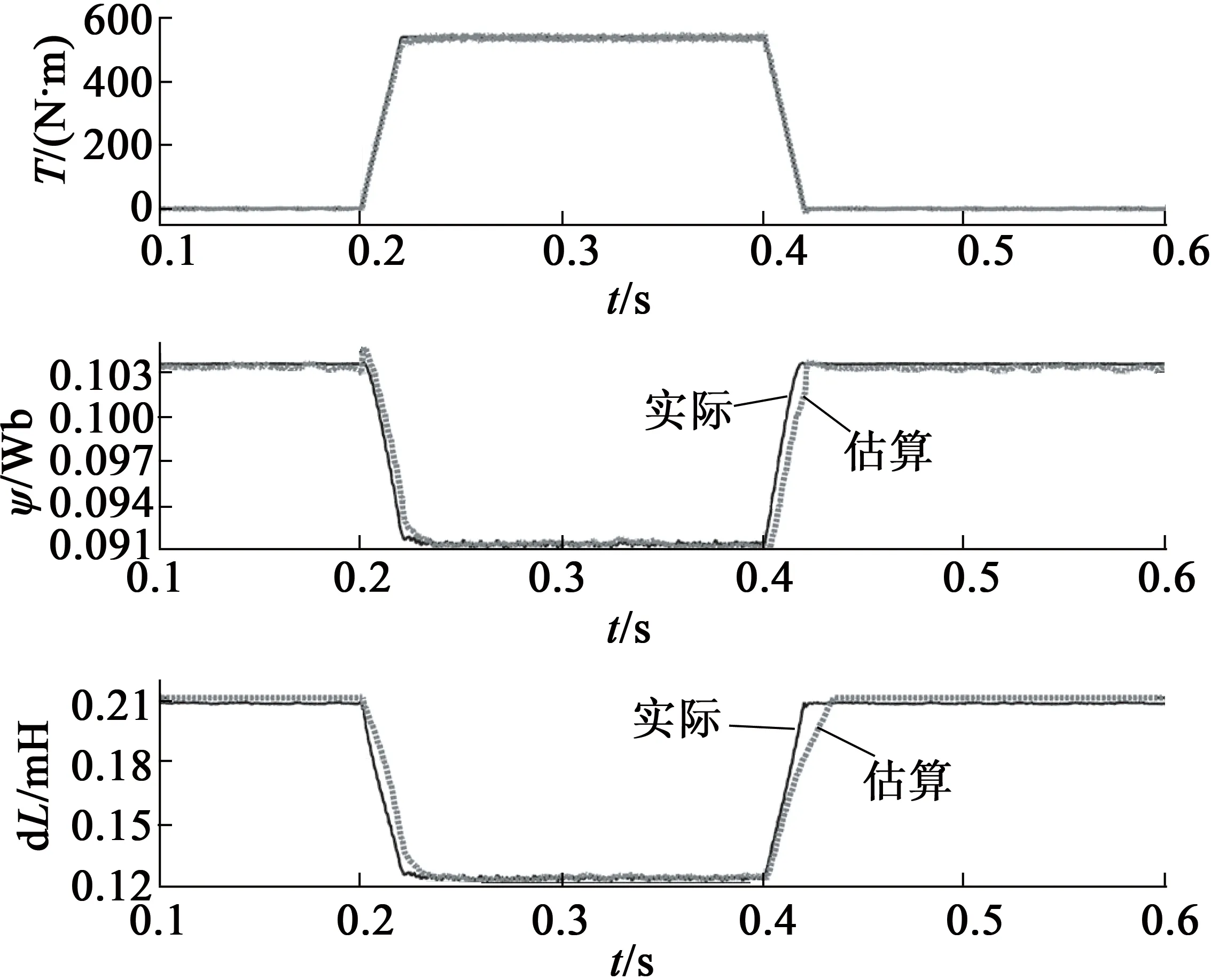
图5 最大转矩(1 000 r/min，540 N·m)工况下磁链和dL估计

由仿真结果可以看出,无论是额定工况还是最大转矩工况，当电机运行稳定时，磁链估计器的输出数值能够较好地跟随磁链参考数值；当磁链发生变化时，磁链偏差最大值在允许的范围内。

同理，无论是额定工况还是最大转矩工况，当电机运行稳定时，ΔL估计器的输出数值能够较好地跟随ΔL参考数值；当ΔL发生变化时，ΔL偏差最大值在允许的范围内。

另外，d轴和q轴电流实际值也可以较好地跟随电流参考值；而且输出转矩同样可以较好地跟随目标转矩，总体上实现了前置永磁同步电机的精确、高效控制。仿真结果表明了本文所述参数估计方法和控制策略的有效性。

3.2 实验验证

为进一步验证上述参数估计方法的有效性，本文进行了相关实验验证。混合动力实验台结构如图6所示，电源选用288 V/180 Ah的LiFePO4电池组；负载选用交流电涡流测功机；前置永磁同步电机参数与表1一致。

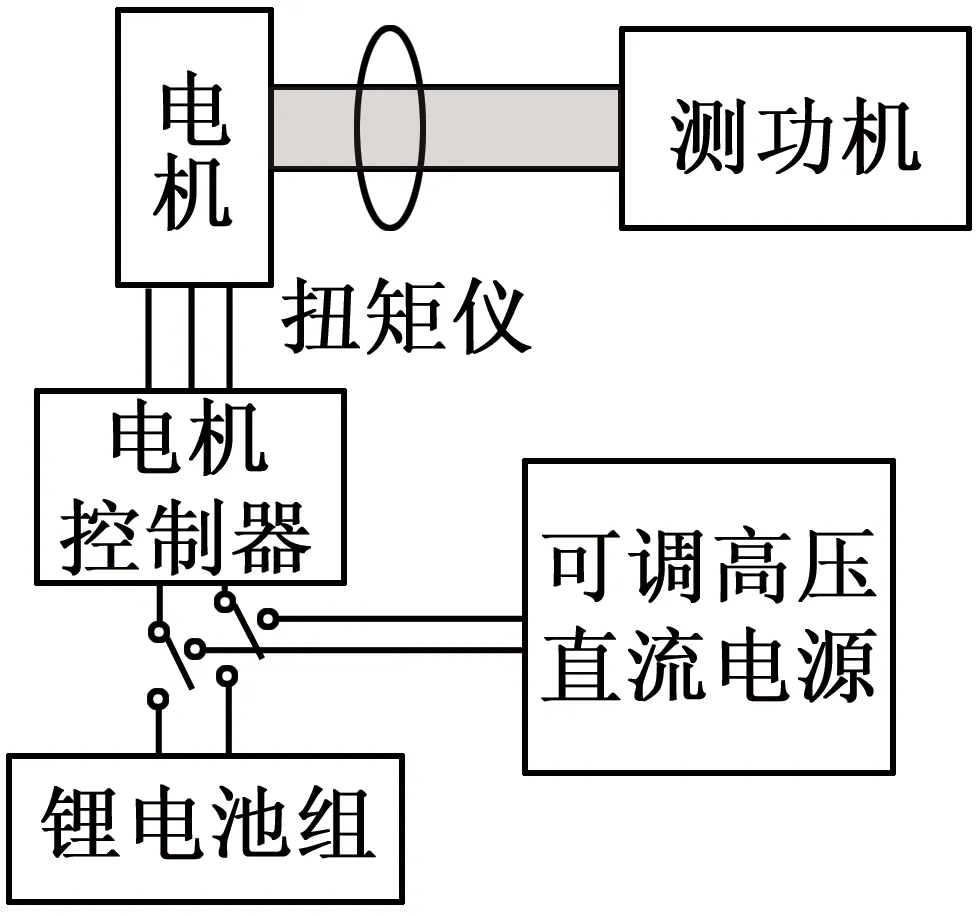
图6 混合动力实验台结构

额定工况(2 000 r/min,358 N·m)和最大转矩工况(1 000 r/min,540 N·m)下的实验结果分别如图7和图8所示。与仿真结果相比，在额定工况下，实验所得磁链估计数值稍大；在最大转矩工况下，实验所得ΔL估计数值稍大。虽然实验条件与仿真条件存在一定的差异，但从实验结果可以看出，实验结果与仿真结果的趋势完全相同。实验结果进一步验证了本文所述参数估计方法和控制策略可以很好地完成磁链和ΔL的估计，并最终实现精确的转矩控制，表明了该方法的有效性。

图7 额定工况(2 000 r/min,358 N·m)下实验结果

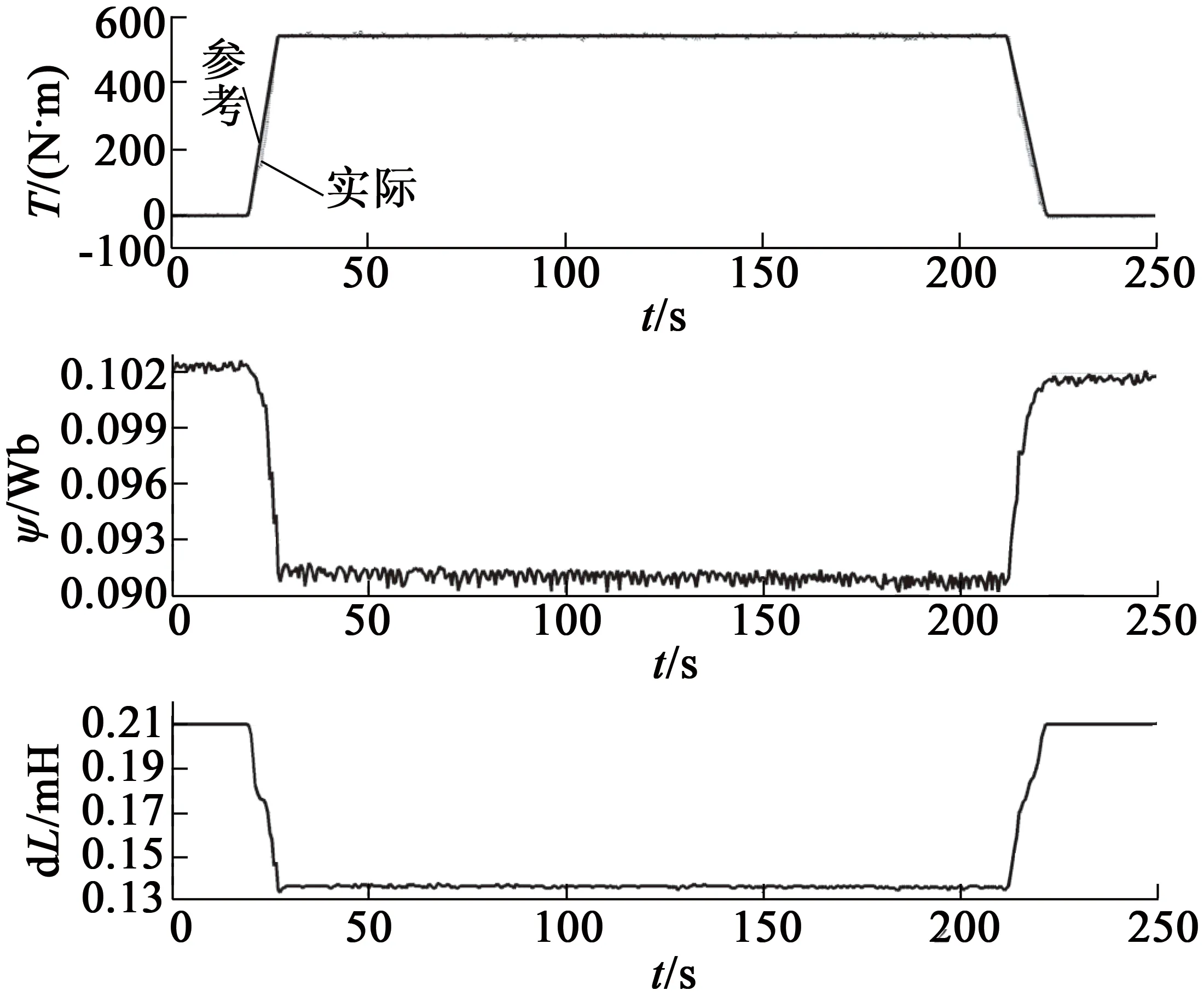
图8 最大转矩工况(1 000 r/min,540 N·m)下实验结果

4 结 语

混合动力汽车作为新能源汽车的主要形式，其首选驱动电机为前置永磁同步电机。虽然前置永磁同步电机具有功率密度大、效率高等优点，但是其控制参数较多，若实现所有参数的匹配、估计和控制，需要采用信号注入法或增加传感器数量，但是上述方法并不适用于车用永磁同步电机。本文通过分析，主要对电机磁链和电感进行估计。首先建立了前置永磁同步电机的数学模型；对于磁链估计，文中采用了前馈式电流解耦算法；对于ΔL估计，文中采用了电机功率闭环控制策略；并将参数估计和MTPA算法结合起来，实现了参数在线估计、转矩控制等。最后通过仿真和实验验证了本文所述参数估计方法的可行性和有效性。所述混合动力汽车用前置永磁同步电机参数估计方法对新能源汽车的驱动系统的控制、优化具有一定的参考意义。

[1] 黄文卿,张幽彤,张兴春.车用永磁同步电机功率闭环扭矩控制方法[J].北京理工大学学报,2015,35(3):246-250.

[2] 王伟光,李伟,陈卫杰.考虑磁钢B-H特性的车用永磁同步电机MTPA控制[J].电力电子技术,2015,49(1):54-56.

[3] 廖勇,伍泽东,刘刃.车用永磁同步电机的改进MTPA控制策略研究[J].电机与控制学报,2012,16(1):12-17.

[4] 武四辈,吴志红,朱元.车用内置式永磁同步电机电感参数辨识方法[J].农业机械学报,2013,44(8):27-32.

[5] LIU K,ZHU Z Q,STONE D A.Parameter estimation for condition monitoring of PMSM stator winding and rotor permanent magnets[J].IEEE Transactions on Industrial Electronics,2013,60(12):5902-5913.

[6] CONSOLI A,SCARCELLA G,SCELBA G,et al.Steady-state and transient operation of IPMSMs under maximum-torque-per-ampere control[J].IEEE Transactions on Industry Applications,2010,46(1):121-129.

[7] KIM S,YOON Y D,SUL S K,et al.Maximum torque per ampere (MTPA) control of IPM machine based on signal injection considering inductance saturation[J].IEEE Transactions on Power Electronics,2012,28(1):488-497.

[8] ESTIMA J O,MARQUES C A J.A new algorithm for real-time multiple open-circuit fault diagnosis in voltage-fed PWM motor drives by the reference current errors[J].IEEE Transactions on Industrial Electronics, 2013, 60(8):3496-3505.

[9] CHEN J L,LIU T H,CHEN C L.Design and implementation of a novel high-performance sensorless control system for interior permanent magnet synchronous motors[J].Electric Power Applications,IET,2010,4(4):226-240.

[10] MORIMOTO S,SANADA M,TAKEDA Y.Effects and compensation of magnetic saturation in flux-weakening controlled permanent magnet synchronous motor drives[J].IEEE Transactions on Industry Applications,1994,30(6):16-32.

[11] QI G,CHEN J T,ZHU Z Q,et al.Influence of skew and cross-coupling on flux-weakening performance of permanent-magnet brushless AC machines[J].IEEE Transactions on Magnetics,2009,45(5):2110-2117.

[12] BOILEAU T,LEBOEUF N,NAHID-MOBARAKEH B,et al.Online identification of PMSM parameters: parameter identifiability and estimator comparative study[J].IEEE Transactions on Industry Applications,2011,47(4):1944-1957.

[13] 郑维.混合动力汽车动力总成参数匹配方法与控制策略的研究[D].哈尔滨:哈尔滨工业大学,2010.

[14] 田硕.柴油机ISG混合动力系统瞬态过程优化控制研究[D].北京：清华大学,2008.

[15] 邓仁燕,唐娟,夏炎,等.基于前馈补偿的永磁同步电机电流环解耦控制[J].电力电子技术,2013,47(6):68-70.

Research on Parameters Estimation Method of IPMSM in HEV Application

MAJian-wei,LIANGXiao-lin,ZHANGPeng-fei

(Xingtai Polytechnic College,Xingtai 054000,China)

The interior permanent magnet synchronous motor (IPMSM) is widely used in hybrid electric vehicle (HEV) with its characteristics such as wide range of constant power, large power density, and high efficiency, etc. Because of the poor working condition and big load mutation of HEV as well as the influence of temperature and magnetic saturation on IPMSM, the control performance was greatly reduced. In order to achieve the precise control of IPMSM, its mathematical model was set up in this paper. The motor torque was related with flux linkage andd,qaxis inductance difference, so the parameters estimation was mainly targeted at flux linkage and inductance. A kind of flux estimation method based on current feed-forward decoupling algorithm was put forward. It can effectively eliminate the influence of condition change on the motor. At the same time a kind ofd,qaxis inductance value estimation algorithm based on power closed loop was also put forward, which can realize the precise control of the motor. The simulation and experimental results verify the effectiveness of the parameter estimation method described in this article.

IPMSM; flux linkage estimation; hybrid electric vehicle

2016-03-04

河北省教育厅青年基金项目(QN20140202);河北省科技计划项目(15212209);河北省教育厅项目(ZD2015015)

TM351

A

1004-7018(2016)08-0035-05

马建伟(1981-)，男，硕士研究生，讲师，研究方向为汽车电气及控制技术。