基于优化算法的城市相邻两交叉口信号配时
李 悦 郝 宇 刘洪涛
(辽宁石油化工大学信息与控制工程学院,辽宁 抚顺 113001)
基于优化算法的城市相邻两交叉口信号配时
李 悦 郝 宇 刘洪涛
(辽宁石油化工大学信息与控制工程学院,辽宁 抚顺 113001)
基于交通车辆流量的分析,以缓解交通拥堵为目的,对某城市相邻两交叉口的交通流量数据进行了调查。将交通流量转化为车队排队长度,以车辆等待时间和穿行时间之和作为目标函数,建立配时数学模型;利用粒子群、差分进化、自适应差分进化等算法,编程求解信号灯最优时间配比。计算与仿真结果表明:该方法优化了绿灯信号时间,提高了相邻两交叉口的通行能力,可有效解决交叉口交通拥堵问题。
智能 交通系统 信号灯 控制 车流量 粒子群算法 自适应 算法
0 引言
随着我国城市化进程的加快、城市道路交通量的日益增加以及城市规模的不断扩大,交通网络矛盾突出,这在一定程度上影响了城市经济发展,并阻碍了人们生活水平的提升。交叉路口是城市道路交通拥挤的瓶颈地带,对其相位信号进行有效控制,能减少交通拥挤、减少交叉路口的交通冲突点、改善交通秩序并提高交通安全性[1]。世界各国普遍使用智能交通系统,通过采取智能信号控制,能有效解决道路交叉路口的拥堵问题。目前,我国大、中型城市的交通管理普遍采用单点定时交通信号灯控制。这种控制方法会在某种程度上造成绿灯时长的浪费,而且会严重延误某些方向上的通行。因此,对交叉路口信号配时进行优化、提高有效绿灯时长是提高交叉路口运行效率的有效方法之一。
目前,大部分研究针对的是单点交叉口的优化。而城市道路网是联动系统,相邻城市主干道的交通能力之间有一定的关联性[2]。因此,针对多交叉口信号配时的优化问题,本文进行了深入研究,主要是分析、优化某市两相邻交叉口A、B的交通流量数据。由于现有的相位配时产生了一定延误问题,在很大程度上制约了道路通行能力,故本文采用PSO、差分进化、自适应差分进化等算法,使相位配时方案得到合理优化。
1 信号配时优化分析
交通信号灯完成一个循环周期所用的时间称为信号周期,即红灯、黄灯和绿灯时间之和,单位为s。在一个周期内,将交叉口各个方向上的相应灯色的组合定义为一个信号相位,且任意一个交叉口的所有相位(相位可以分为两相位和四相位)一般都采用相同的信号周期[2]。通常,信号灯最小周期时长不小于40 s,否则交叉口各个方向的交通需求难以得到满足;而最大周期时长不大于120 s,否则会导致交叉口处的车辆等待时间过长。
由经验分析得出,信号配时优化的关键是确定周期时间和每个相位的绿灯时间。根据传统的Webster配时优化公式[3],得到最佳信号周期如下:
(1)
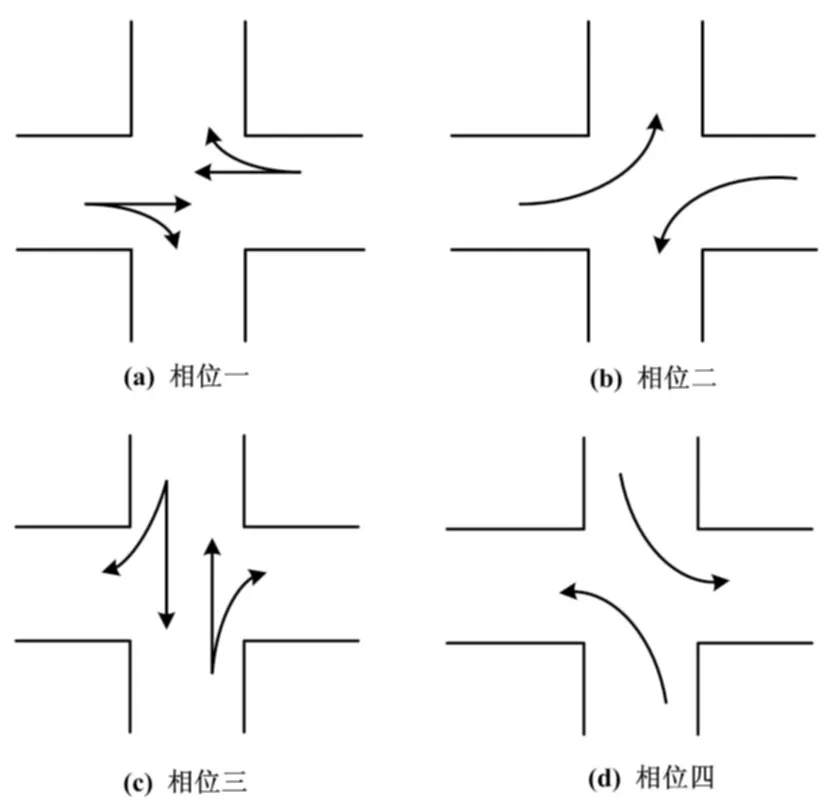
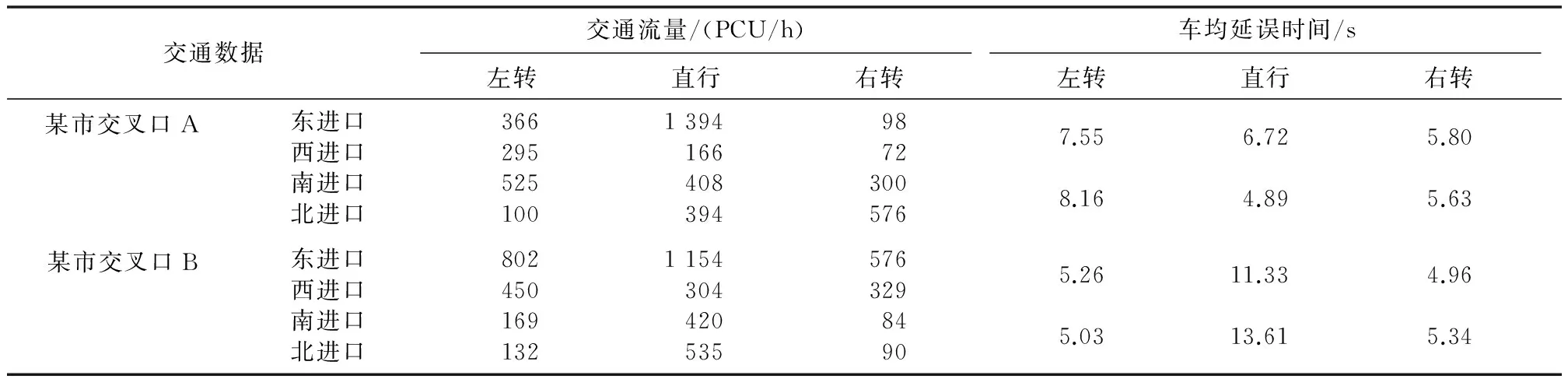
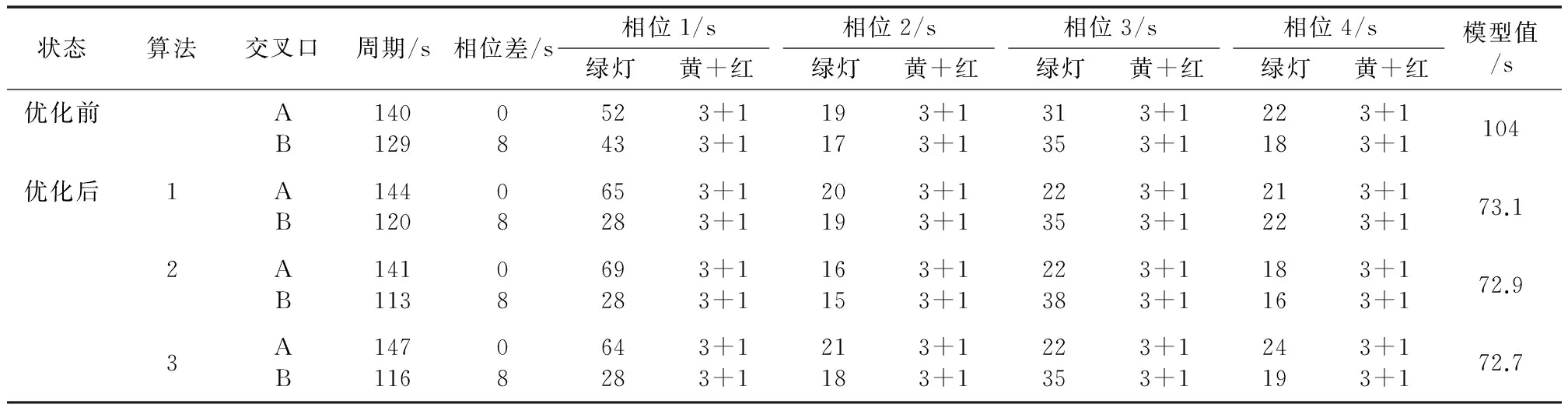
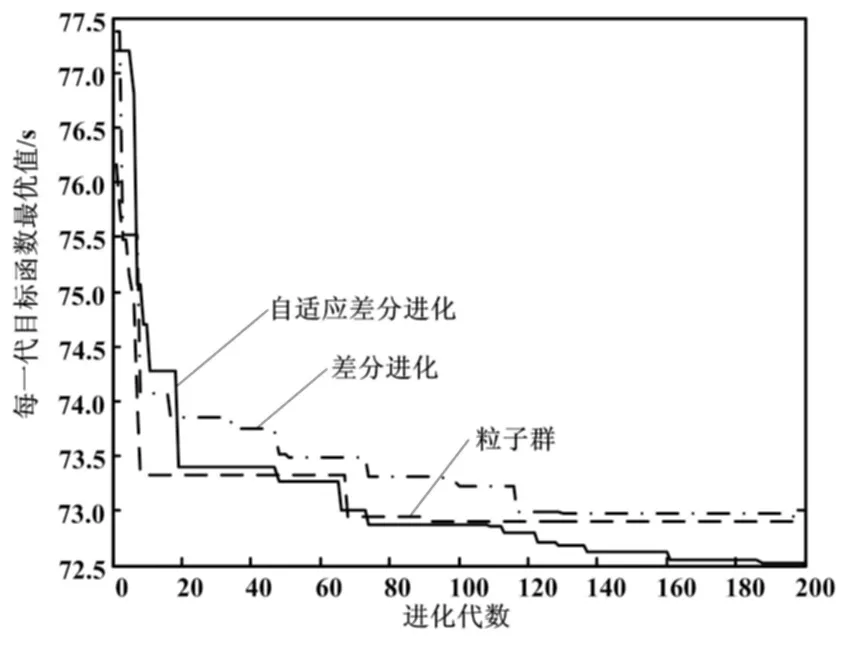
(2)式中:C为信号周期,s;L为总损失时间,s;Y为一个周期的全部信号相位的各个最大yi值之和;Gi为韦伯斯特公式计算的第i相位的绿灯时间,Gmin 对于多交叉口,假设第i个路口为开始路口,第(i+1)个路口为终止路口, 两相邻交叉口都采用四相位方案,交叉口A、B四相位方案如图1所示。图1中,箭头表示相位,即在该方向的车道为绿灯,无箭头的车道为红灯。 现分别考虑两个交叉口。如只考虑交叉口i,当车到达的时间在该车要通过的相位绿灯时间和相邻相位转换到该相位绿灯时间之间,则车可通过该路口;当车到达时间小于别的相位转换到该车所在相位时间,则该车不能通过。 为方便描述,下文中下标ijk表示第i个交叉口、第j个路口、第k相位,ijkm表示第i个交叉口、第j个路口、第k相位的第m辆车,Ci和Ci+1分别表示相邻 交叉口的信号周期[4]。 图1 四相位方案图 在0~nCi周期内,第i个交叉口、第j个路口、第k相位的第m辆车的排队等待时间wijkm为: (3) 式中:aijkm为第i个交叉口、第j个路口、第k相位的第m辆车的到达时间;Gix为第i个交叉口、第x相位的绿灯时长;l为相位转换时的时间间隔[5],即相位差,这里l是常数;i=1,2;j=1,2,3,4;k=1,2,3,4。 当以两个路口为一个系统时,该车离开该路口所用时间为:到达该车所在相位方向停止线的时间加上该车离开上一路口所用的时间。 在0~nCi周期内,第i个交叉口、第j个路口、第k相位的m辆车离开系统的时长Tijkm为: (4) 式中:tik为第i个交叉口、第k相位的车辆从排队系统通过交叉口停止线所需的时间;Lijk为车辆排队长度;v为车辆正常行驶时间;v′为队列的消散速度;D为交叉口之间距离。 通过上述分析可知:两个十字路口相关联处为交叉口A东进口这一通道。假设:Lijk为第i个交叉口、第j个路口、第k相位的车辆排队长度;uijk为第i个交叉口、第j个路口、第k相位车辆排队期望最大长度。由此可以得到车辆排队长度的计算公式见式(5)。 式(5)右边比值关系为该相位非绿灯时间与车辆整个等待时间之比。等待时间所占比例越大,则后续到达车辆越多、车队越长。车辆排队期望最大长度依据车流量的多少和实际情况合理取值,通过该式将交通流量转化为车辆排队长度。 综上所述,本模型以各交叉口的各相位绿灯配时作为控制变量。为保证车辆在此系统中所延误的时间最短,即以车辆在十字路口处等待时间与通过路口时间之和最小作为优化目标,目标函数见式(6)。 (5) (6) 式(6)的约束条件为: 3.1 粒子群算法分析 PSO算法采用实数求解,是一种通用的全局搜索算法,其优点主要在于其思想简单,在程序上容易实现[5]。假设目标函数式(6)的搜索空间在D维度,粒子群中粒子的规模为m,那么第i个粒子的位置可以用一个D维向量表示xi=(xi1,xi2,…xiD)T,其中i=1,2,3,…,m;粒子的速度用D维向量表示vi=(vi1,vi2,…,viD)T。在粒子群算法中,每个粒子的位置均为目标函数的一个潜在解,将xi代入目标函数就可以得到该粒子的适应值,然后在每一代迭代过程中汇总根据目标的适应值,以衡量粒子的优劣,循环判断迭代终止条件。进行200次迭代后,得到目标函数的最优值。 3.2 差分进化算法分析 差分进化算法是一种基于群体进化的遗传算法[6],对于本文的最小化函数优化问题而言,采用标准DE算法可以基于实数编码并寻优,经过变异、交叉和选择[7-8],最终得到最优解。对目标函数式(6)而言,每一个个体均对应问题的一个解。标准DE进化算法如下。 ①随机生成N个解作为初始种群并评价。 ②对于每个个体xi,随机选择两个不同的个体相减生成差分矢量,将差分矢量附权值后加到第三个随机选择的个体上,生成变异矢量。 ③随机选择另外三个解执行变异操作,生成临时解ti。 ④将临时个体与当前个体交叉生成新解vi。 ⑤如果终止条件满足,则输出最优解,否则返回步骤②。 在这里,初始种群规模Np=50,最大迭代次数Gm=200。 3.3 自适应差分进化算法分析 自适应DE算法[9]是在标准DE算法的基础上,提出的一种采用变异策略的自适应和控制参数的自适应的优化算法。其步骤如下。 ①初始化:生成原始种群S0与控制参数种群S1,最大迭代次数200,种群规模Np=50。 ②原始种群S0的进化。 ③控制参数种群S1的进化。 ④重复步骤②和步骤③,直到进化代数超过最大进化代数Gm。 经调查和数据采集,得到交叉口A、B的交通流量和车均延误时间现状如表1所示(表中PCU/h表示每小时的标准小汽车当量)。交叉口优化前、后的配时方案对比如表2所示。优化前,算法的输出是所有阶段的绿灯时间[10],利用所建立的数学模型并依据PSO算法、差分进化算法以及自适应差分进化算法,分别对相邻两交叉口的绿灯时长进行M[11]仿真求解并进行对比,重复求解10次,最终得到优化后的时间配比方案。其中:算法1代表粒子群算法,算法2代表差分进化算法,算法3代表自适应差分进化算法。 由表2可知:目标函数的模型值由优化配时前的104 s减少到73 s左右,即车辆在十字路口处等待时间与通过路口时间之和以及车均延误时间最优,大大缓解了交叉口交通拥挤问题。三种算法得到的模型值基本相同,证明了模型的通用性和可行性。 表1 交通数据现状 表2 优化前、配时方案对比 优化后的绿灯时间使车辆的通行能力最强,车辆在规定的周期内全部顺利通过,减少了车辆的等待时间。三种算法优化图如图2所示。通过200次迭代,算法最终收敛到最优值。 图2 三种算法优化图 本文在Webster优化配时公式的基础上,以各交叉口的各相位绿灯配时作为控制变量,以相邻交叉口车辆等待时间和穿行时间之和作为目标函数,建立了一种通用相邻交叉口配时优化模型。以某市相邻两交叉口A、B为例,进行数据采集,并利用差分进化算法及其他两种对比算法进行仿真研究。仿真结果表明,优化后的模型值与优化前的相比有很大改善。三种算法得到的模型值基本相同,证明了模型的通用性和可行性。 [1] 王沈平,蔡家明. 多相位交通信号配时的模糊控制方法[J].上海工程技术大学学报,2009,23(4):312-316. [2] 何佳佳. 基于蚁群算法的交通信号配时优化[D].西安:陕西科技大学,2012. [3] 王秀旺,毛新娜. 优化交通信号配时,缓解城市交通拥堵[J].大学数学,2012,28(3):87-91. [4] 林荔娜. 城市多交叉口信号配时优化[J].莆田学院学报,2014,21(2):82-86. [5] 郭香军.粒子群算法的改进研究[D].燕山:燕山大学,2011. [6] 王凌,钱斌. 混合差分进化与调度算法[M].北京:清华大学出版社,2012. [7] 熊伟丽,刘欣,陈敏芳,等.基于差分蜂群算法的无线传感器网络节点分布优化[J].控制工程,2014,21(6):1036-1040. [8] 简献忠,严军,范建鹏,等.基于差分进化算法的光伏阵列MPPT控制方法[J].控制工程,2014,21(4):559-566. [9] 赵树本,张伏生,钟继友,等.自适应差分进化算法在电力系统无功优化中的应用[J].电网技术,2010,34(6):170-173. [10]LI Y,GUO X C,TAO S R,et al. NGSA-Ⅱbased traffic signal control optimization algorithm for over-saturated intersection group[J].Journal of Southeast University,2013,29(2):211-216. [11]Holly Moore. Matlab实用教程[M].2版.北京:电子工业出版社,2010. Time Assignment Based on Optimization Algorithms for Urban Traffic Lights at Two Adjacent Intersections Based on the analysis of the traffic flow,in order to ease traffic congestion,the traffic flow data at two adjacent intersections of a certain city are surveyed. The traffic flow is transformed into the queuing length of the motorcades,while the sum of vehicle waiting time and passage time is selected as the objective function for setting up the mathematical model of time assignment. The optimal ratio of time assignment is derived by using particle swarm,differential evolution and the adaptive differential evolution algorithms. The results of calculation and simulation show that the method optimizes the time for green lights,so improves the traffic capacity of two adjacent intersections. The conclusion indicates that using optimization algorithms can resolve the problem of traffic congestion at intersections. Intelligent Transportation system Traffic light Control Vehicle flow PSO Self-adaption Algorithm 李悦(1972—),女,2014年毕业于辽宁石油化工大学控制工程专业,获硕士学位,实验师;主要从事预测控制方向的研究。 TH-3;TP273+.1 A 10.16086/j.cnki.issn 1000-0380.201608025 修改稿收到日期:2016-01-13。2 配时优化模型建立
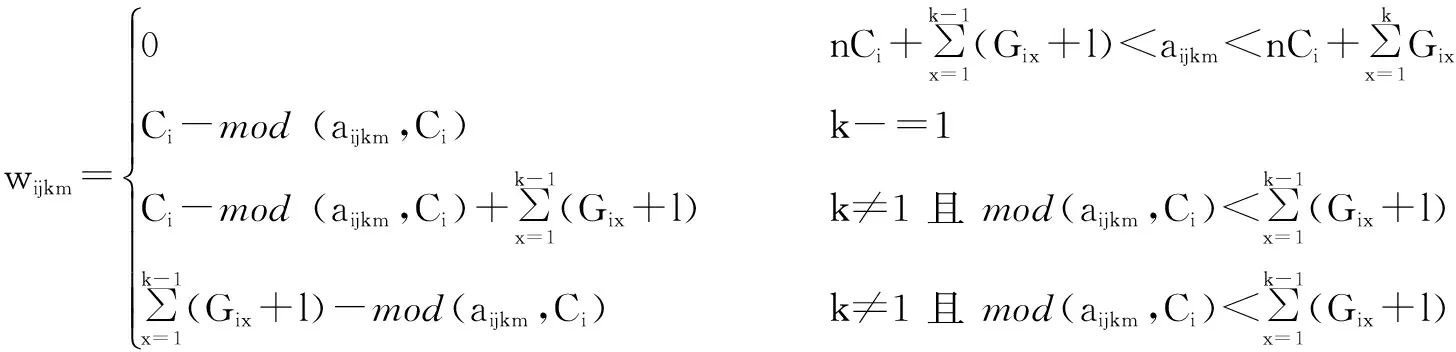
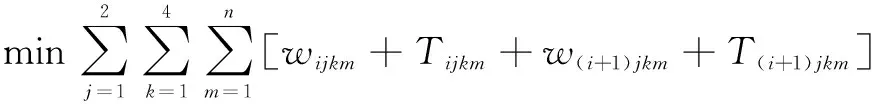
3 利用优化算法分析计算
4 优化仿真
5 结束语
——国外课堂互动等待时间研究的现状与启示

