一种自适应卡尔曼滤波在动态导航定位中的应用

周 敏 刘 健 杨 林 王宇龙 桑青松

(武汉工程大学电气信息学院，湖北 武汉 430205)



一种自适应卡尔曼滤波在动态导航定位中的应用

周 敏 刘 健 杨 林 王宇龙 桑青松

(武汉工程大学电气信息学院，湖北 武汉 430205)

在实际运行过程中，往往很难预测目标的运动状态，这就会导致应用在动态导航定位中的卡尔曼滤波算法难以收敛。为了解决这个问题，提出了一种新的自适应卡尔曼滤波算法。该算法采用卡方分布构造统计量，通过检验动力学模型是否出现异常，确定了一种平衡观测方程和状态方程的自适应因子。仿真结果表明，在目标状态发生变化的情况下，该方法优于标准卡尔曼滤波算法和两段函数确定的自适应因子的卡尔曼滤波算法，是一种鲁棒性好、性能可靠、精度高的滤波算法，可广泛应用于动态导航定位中。

动态导航 定位 卡尔曼滤波 自适应 动力学模型 算法

0 引言

卡尔曼滤波算法被广泛应用于动态载体的导航与定位中。当载体进行规则运动且系统噪声的统计特性已知时，卡尔曼滤波将会是最优滤波。但是载体在实际运行过程中，很难确定噪声的统计特性，而且一般也很难保证规则运动，这往往会导致系统滤波模型与真实模型之间存在一定的偏差，使导航解算的解严重偏离真实解。

为了解决以上问题，提出了自适应卡尔曼滤波算法并将其应用于动态导航定位中，同时涌现出了许多求解自适应因子的方法。文献[1]介绍了一种利用相关法实现的QR自适应滤波方法；文献[2]提出了一种改进的Sage自适应滤波方法，这类方法需要观测信息同维、同类；杨元喜等提出了一种更为灵活的自适应滤波方法[3],利用四种判别统计量和四种自适应因子构造出用于平衡观测值和一步预测值的自适应滤波方法，但是当观测信息严重不足时，采用该方法确定的自适应因子不能很好地控制载体异常扰动；文献[4]提出了一种直接对动力学模型误差参数进行在线估计的方法。

合理的最优自适应因子应该使自适应滤波器的理论统计特性与实际观测值的统计特性尽量保持一致[5],如状态向量滤波值的协方差阵、状态向量预测值的协方差阵以及新息向量的协方差阵。而最优自适应因子的求解可以利用卡方分布构造一个统计量来实现。由此，可以在一定的置信水平下，通过假设检验来判断滤波是否出现异常，从而对模型进行自适应调节。

为了解决动态导航定位中存在的观测信息严重不足、系统动力学模型与真实动力学模型之间存在偏差等问题，本文提出了一种新的自适应卡尔曼滤波算法(adaptive Kalman filtering algorithm,AKTA)。该算法在自适应卡尔曼滤波原理的基础上，利用卡方分布构造一个统计量，同时给出了卡方分布检验准则以及确定自适应因子的计算方法。通过仿真，将该方法与经典卡尔曼滤波算法(conventional Kalman filtering algorithm,CKFA)和两段函数确定的自适应因子的卡尔曼滤波算法进行对比，验证了该算法在动态导航与定位中的有效性及其滤波精度高的优点。

1 自适应卡尔曼滤波原理

在动态导航与定位中，卡尔曼滤波器一般用线性化后的离散模型来描述[6-7]：

(1)式中：Xk为k时刻的状态向量；Φk,k-1为从(k-1)时刻到k时刻的状态转移矩阵；Wk为k时刻的系统误差向量；Zk为k时刻的观测向量；Ak为k时刻的系数矩阵；Vk为k时刻的观测误差向量。Wk、Vk须满足以下性质：E(Wk)=0,D(Wk)=∑Wk；E(Vk)=0,D(Vk)=∑k;Cov(Wk, Wj)=0, k≠j; Cov(Vk, Vj)=0, k≠j, Cov(Wk, Vj)=0。式中：∑Wk为k时刻的过程噪声方差阵；∑k为k时刻的测量噪声方差阵。

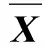
(2)

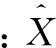
(3)

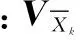
自适应滤波原理为[8]：

(4)

(5)

2 动态导航中的自适应滤波

目前，卡尔曼滤波算法是在动态导航应用中较常用的方法。滤波器在某时刻输出的结果是在观测值和预测值之间的一个权衡。当动力学模型发生扰动而观测值比较准确时，如果预测值仍然分配较大的权，这将会使定位结果严重偏离真实值，甚至造成滤波无法收敛。和文中第1节类似地引入一个自适应因子αk，使预测值的权分配得小一些，只是求解αk的方法不同。因此，在式(2)的基础上可作如下改动，并得到第k个历元的预测误差及其新息向量方差为：

(6)

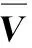
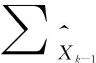
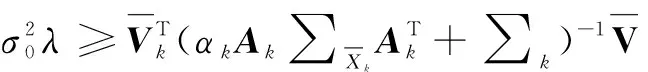
3 算例分析

为了验证本文所提出的自适应卡尔曼滤波在动态导航与定位中应用的有效性，采用以下条件进行仿真测试。假设载体在X轴方向运动，在0～100 s以0.5 m/s2的加速度作匀加速运动，在100～400 s以大约50 m/s的速度作匀速运动，在400～500 s以-0.3 m/s2的加速度作匀减速运动，在500～800 s以大约20 m/s的速度作匀速运动，在800～900 s以加速度方差为1 m/s2作机动运动，在900～1 500 s以大约26 m/s速度作匀速运动。直接在轨迹发器的位置和速度输出上叠加白噪声信号来模拟X轴方向上的位置和速度。位置误差方差取为1 m2,速度误差的标准差为0.1m/s。

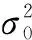
(8)

式中：c为常量，一般在1.0～2.5之间；ΔVk为预测残差统计量。

图1是各种方案在X轴方向的位置残差(Ex)；图2是方案二和方案三的自适应因子对比图；表1是三种滤波算法的均方根误差(root mean square error,RMS)比较。图1(c)和图2(b)是选取置信水平在0.01情况下的基于卡方分布的滤波残差波形和自适应因子的波形。

根据图1和表1可以看出，在0～100 s、400～500 s以及800～900 s时，载体分别在作加速、减速和机动运动，使滤波模型的状态方程与实际运动的状态方程不相符，导致CKF后的残差较大，整体效果欠佳。

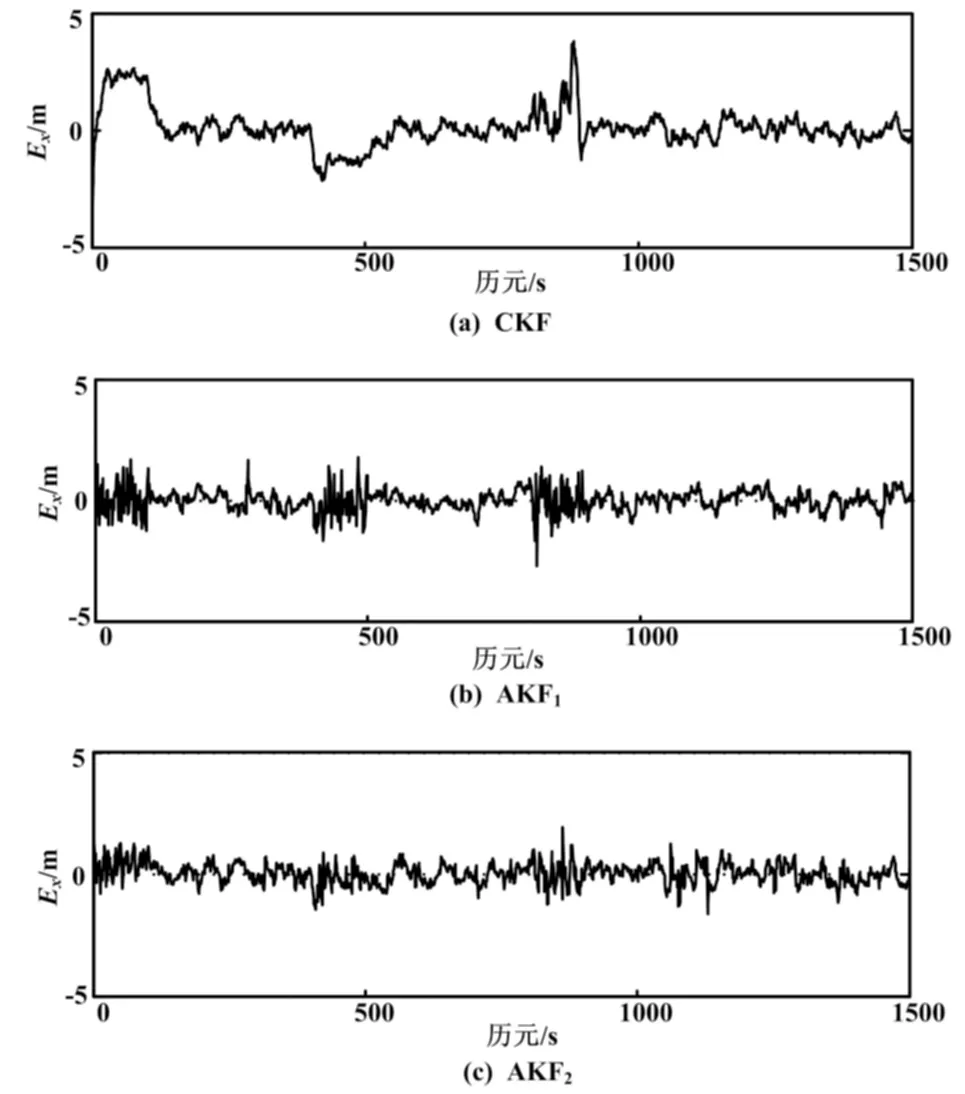
图1 X轴方向的位置残差对比图

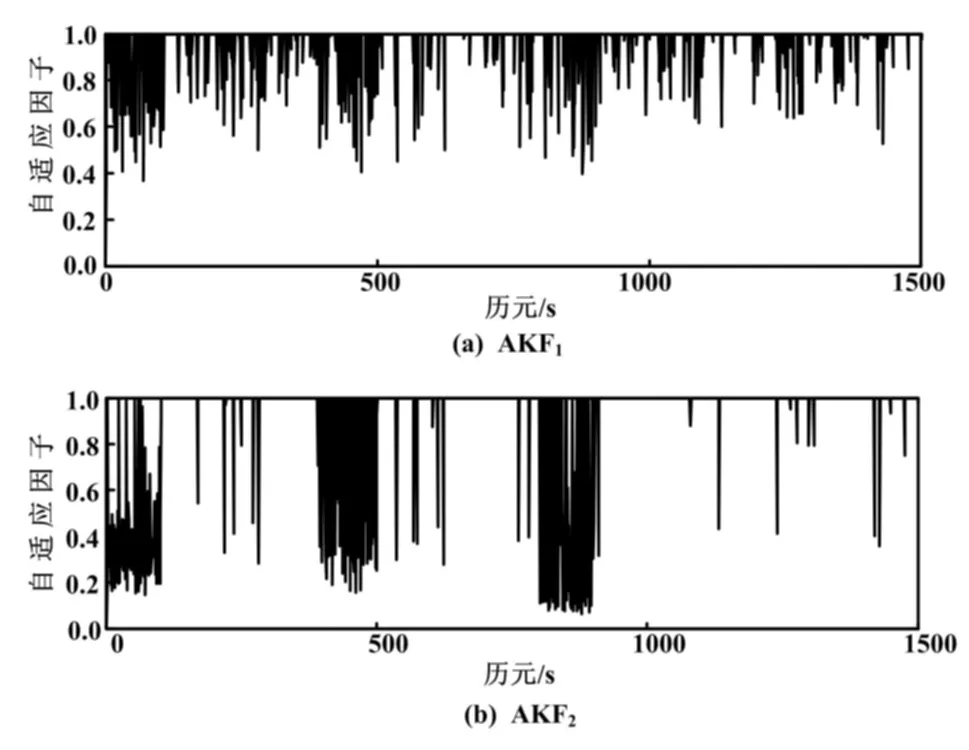
图2 自适应因子对比图

RMSCKFAKF1AKF2γ=0.01γ=0.05γ=0.10位置/m0.81550.44680.38160.41450.4207速度/(m/s)0.15360.12900.09300.09310.0823

根据图1和表1可以看出：相对于CKF,AKF1能有效地控制载体异常扰动，且经过AKF1处理后的位置均方根误差为0.446 8 m，远小于经CKF处理后的位置均方根误差。

图1表明:AKF2可以有效控制运动载体在三个“特殊”时段滤波误差的增大，阻止了卡尔曼滤波的发散，但这是以降低滤波精度为代价的。当动态解算的观测信息不足时，AKF2的解算残差要小于AKF1。由表1可知：AKF1的位置均方根误差为0.446 8 m，而AKF2的位置均方根误差为0.381 6 m。但是AKF2的计算量要比AKF1大一些，这是因为AKF2在计算自适应因子时采用了迭代计算。

根据图2可知：在动力学模型异常的三个时段，AKF1的自适应因子最大衰减可以达到0.4，平均衰减可以达到0.5左右；而AKF2的自适应因子最大衰减可以达到0.2，平均衰减在0.3左右。因此在相同模型误差的情况下，AKF2更能较好地遗忘动力学模型误差。而在其他时段，基于卡方分布检验的自适应因子比两段函数确定的自适应因子衰减更小，这将会增加AKF2在导航解算时对动力学模型的依赖，使滤波结果更接近真实值。

4 结束语

本文研究了一种自适应卡尔曼滤波算法在动态导航与定位中的应用，并且将该算法与标准卡尔曼滤波、两段函数法进行了比较与分析。仿真结果表明，当运动目标状态发生变化且观测信息不充足时，该算法能更好地控制模型误差对导航解的影响，并更有效地控制载体的异常扰动、提高滤波的精度。该方法比文献

[5]计算自适应因子的方法更易于实现。因此，该方法可被广泛应用于动态导航与定位，对于解决观测异常和状态异常等问题具有重要的研究价值。

[1] 宁少武,史治宇. QR分解的最小二乘格型自适应滤波算法在噪声主动控制中的应用[J].振动工程学报,2013,26(3):363-373.

[2] 徐婷婷. VTS系统船舶跟踪和预测的新技术研究[D].大连：大连海事大学,2012.

[3] 杨元喜,任夏,许艳.自适应抗差滤波理论及应用的主要进展[J].导航定位报,2013,1(1):9-15.

[4] 高为广,张晓东.基于Kalman滤波的动力学模型误差估计算法[J].测绘科学,2011,36(2):56-58.

[5] 宋迎春.抗差自适应滤波中带有置信度的自适应因子设计[C]//第一届中国卫星导航学术年会论文集,北京：2010,1310-1316.

[6] 于静文,薛蕙,温渤婴.基于卡尔曼滤波的电能质量分析方法综述[C]//电网技术,北京：2010,34(2):97-103．

[7] 王笑天,杨志家，王英男，等.双卡尔曼滤波算法在锂电池SOC估算中的应用[J].仪器仪表学报,2013,34(8):1732-1738.

[8] 陈远,张小红,郭斐,等.自适应卡尔曼滤波在GPS/DR组合导航中的应用[J].测绘科学,2010,35(3):169-170.

[9] HIDE C,MOORE T,SMITH M. Adaptive Kalman filtering algorithms for integrating GPS and low cost INS[J]．Position Location and Navigation Symposium,2004:227-233.[10]Da R.Failure detection of dynamical systems with the state chi-square test [J].Journal of Guidance Control and Dynamics,1994,17(2):271-277.

[11]王双红,聂建亮.自适应交互集合Kalman滤波的动态精密单点定位[J].自动化仪表,2013,34(5):10-12.

Application of an Adaptive Kalman Filtering Algorithm in Dynamic Navigation Positioning

In actual operation process of target,the dynamic motion state of the target is difficult to be predicted,which makes the Kalman filter algorithm applying in dynamic navigation positioning difficult to converge. In order to solve the problem,a new adaptive Kalman filtering algorithm is proposed. The chi square distribution is used to construct statistics,through checking if the dynamics model is abnormal or not,the adaptive factor of equilibrium observation equation and state equation is designed. The results of simulation show that in the case of the target state charging,this method outperforms the standard Kalman filtering algorithm and the Kalman filtering algorithm that the adaptive factor is determined by two-segment functions,so it is a kind of filtering algorithm with good robustness,reliable performance and high accuracy,and can be used widely in dynamic navigation positioning.

Dynamic navigation Positioning Kalman filter Self-adaption Dynamics model Algorithm

国家自然科学基金资助项目(编号：51207117)；湖北省教育厅科学研究基金资助项目(编号：Q20141503)。

周敏(1990—)，女，现为武汉工程大学检测技术与自动化装置专业在读硕士研究生；主要从事模式识别与智能系统方向的研究。

TH86;TP274

A

10.16086/j.cnki.issn 1000-0380.201608001

修改稿收到日期：2015-12-22。