解析几何中的定点定值问题的策略与方法

筅江苏省徐州高级中学　田淑华

解析几何中的定点定值问题的策略与方法

筅江苏省徐州高级中学田淑华

在近几年的高考中，有关解析几何的定点、定值问题频频出现，该类问题知识综合性强，方法灵活，对运算能力和推理能力要求较高，因而成为了高中数学学习的重点和难点.定点、定值问题都是探求“变中有不变的量”.因此要用全面的、联系的、发展的观点看待并处理此类问题.从整体上把握问题给出的综合信息，并注意挖掘问题中各个量之间的相互关系，恰当适时地运用函数与方程、转化与化归、数形结合、分类讨论、特殊到一般、相关点法、设而不求、换元、消元等基本思想方法.下面笔者通过具体的例子来说明这类问题的求解.

一、定点问题

定点问题一般借助椭圆或圆的性质、直线与圆的位置关系、平面向量等基础知识，考查运算求解能力、推理论证能力，同时考查转化化归思想、数形结合思想、函数与方程思想.

例1在平面直角坐标系xOy中，记二次函数f（x）= x2+2x+b（x∈R）与两坐标轴有三个交点.经过三个交点的圆记为C.

（1）求实数b的取值范围；

（2）求圆C的方程；

（3）问：圆C是否经过定点（其坐标与b无关）？请证明你的结论.

解析：（1）（2）略.

（3）方法1（特殊一般法）：由（2）知，圆C的方程为x2+ y2+2x-（b+1）y+b=0.分别令b=0，-1，得方程组或

所以圆C过定点（0，1）和（-2，1）.证明如下：

将点（0，1）的坐标代入方程，左边=02+12+2×0-（b+1）+b=0，右边=0，所以圆C过定点（0，1）.

同理可证圆C过定点（-2，1）.

方法2（参数无关法）：圆C必过定点，证明如下：

假设圆C过定点（x0，y0）（x0，y0不依赖于b），将该点的坐标代入圆C的方程，得++2x-y+b（1-y）=0（*）.000

为使（*）式对所有满足b<1（b≠0）的b都成立，必须有1-y0=0，结合（*）式得解得或

经检验知，点（0，1）、（-2，1）均在圆C上，因此圆C过定点.

评注：定点问题通常先求出动曲线方程，而后求定点有两种方法：方法1通过取特殊值找出定点，然后加以证明；方法2利用定点与参数无关，从而含参数的动圆方程恒成立，利用系数关系求出定点.

二、定值问题

在近几年的高考和高考模拟试题中有很多解析几何问题由于所给问题有很好的对称和对等性，其运算过程也具有很好的对偶性.如果能够充分利用其内在的美学因素，配合正确的解题策略，那么运算就会更加自然流畅.

1.运用设而不求的思想求解例2如图1，在平面直角坐标系xOy中，已知A、B、C是椭圆=1（a>b>0）上不同的三点，A2，B（-3， -3），点C在第三象限，线段BC的中点在直线OA上.

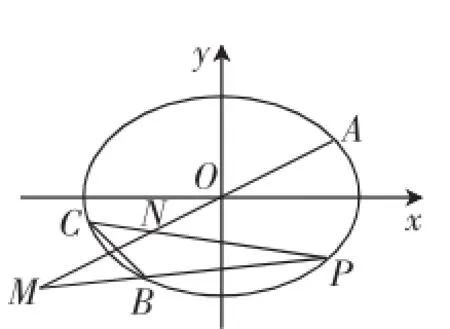
图1　

（1）求椭圆的标准方程；

（2）求点C的坐标；

（3）设动点P在椭圆上（异于点A、B、C），且直线PB、PC分别交直线OA于M、N两点，证明为定值并求出该定值.

解析：（1）（2）略.

设P（x0，y0），M（2y1，y1），N（2y2，y2）.

从而y1y2=

评注：本题考查曲线与方程、直线与曲线的位置关系，考查运算能力，考查数形结合、函数与方程等数学思想方法.第（3）问中设出点P、M、N的坐标，建立等量关系求解，体现“设而不求”思想.

2.通过设坐标求解

定值问题，先设出动点的坐标，并看作参数，再根据条件依次求出相关量，建立与参数的联系，将椭圆上点的坐标满足椭圆的方程这一基本条件代入消参.

图2　

例3如图2，M、P是圆O：x2+ y2=r2（r>0）上任意两点，圆O上的点N与点M关于x轴对称，直线MP、NP分别与x轴交于点A和点B，求证：A、B两点的横坐标之积为定值.

证明：设M（x1，y）1，P（x2，y2），则N（x1，-y1），且

设点A横坐标为xA，点B横坐标为xB，由M、P、A三点共线得，于是

用-y1替换y1得x，所以xAxB=

综上，A、B两点的横坐标之积为定值r2.

三、定位问题

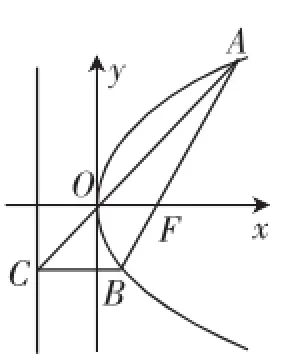
图3　

例4如图3，设抛物线y2=2px（p>0）的焦点为F，经过点F的直线交抛物线于A、B两点.点C在抛物线的准线上，且BC∥x轴.证明：A、C、O三点共线.

证明：因为抛物线y2=2px（p>0）的焦点为所以经过点F的直线AB的方程可设为x=my+，代人抛物线方程得y2-2pmy-p2= 0.若记A（x1，y1），B（x2，y2），则x1、y2是该方程的两个根，所以y1y2=-p2.因为BC∥x轴，且点C在准线x=-上，所以点C的坐标为故直线CO的斜率为k=即k也是直线OA的斜率，所以直线AC经过原点O.即证得A、C、O三点共线.

评注：本题考查抛物线的概念和性质、直线的方程和性质，以及学生的运算能力和逻辑推理能力.也可直接利用抛物线的几何性质结合平面几何相似比例求解.它直观简明，避免计算量大，是解答小题的首选方法，也是解答大题的重要方法.

四、最值与范围问题

解析：设直线PQ的方程为x=c+my，P（x1，y1），Q（x2，y2），将直线方程代入椭圆方程得（b2m2+a2）y2+2b2cmy-b4= 0.故y1+y2=-

而△F1PQ的面积S=c|y1-y2|=c

令t=m2+1（t≥1），则S=2ab

评注：以上两题考查直线与椭圆的位置关系，并结合基本不等式求最值或范围.

通过以上几个典型例题的分析，我们可以得到解析几何中的定点、定值问题的方法：求出动曲线的方程，根据方程可由特殊一般法或者运用参数方程消参法确定定点.而最值与范围问题的方法通常是从函数、基本不等式及几何意义这三个方面去考虑.

总之，定点、定值问题是解析几何的一个难点，是多年来高考的一个热点.这类问题在高考中常以解答题的形式出现，又时常具有压轴性质，因此是众多考生、教师、专家与学者关注的一个焦点.定点的问题往往表现为“直线过定点”、“曲线过定点”、具有某种性质的点为定点等，定点的坐标为定值；定值的问题往往表现为求解或证明某个数学表达式为定值.定点、定值问题都需要根据条件、定义、定理、性质、结论等，经过计算、推理、论证等确定某点的坐标，或某个数学表达式为常数，此常数与变量或参数无关.只要我们在平时的解题实践中多总结、多反思就能不断地积累解题经验，提高解题能力.F