以图导思方向明，完美解答自然生——武汉市2016届高三四月调考理科压轴试题的解法探讨

筅湖北省武汉市黄陂区第一中学盘龙校区　李红春

筅湖北省武汉市教育科学研究院　孔峰

以图导思方向明，完美解答自然生——武汉市2016届高三四月调考理科压轴试题的解法探讨

筅湖北省武汉市黄陂区第一中学盘龙校区李红春

筅湖北省武汉市教育科学研究院孔峰

每年的高三调考试题是命题专家匠心独运之作，尤其是压轴题中的函数导数题，其方法多样、思想灵活，具有鲜明的导向性，备受一线教师的青睐.由于压轴试题难度大，不少教师只能依赖参考答案为学生解惑，照本宣科的讲解，让很多学生知其然，却不知其所以然.其实很多冰冷的标准答案背后都有着鲜活的思考.笔者有幸参与武汉市高三调考试题的命制，和多位专家亲切交流，感受颇深.现以武汉市2016届高三四月调考理科函数导数试题为例，将求解过程中的心路历程真实呈现出来，希望能对一线教师的教学和命题有所借鉴.

题目：H（x）=x2ex-lnx（.ln2≈0.693，≈1.649）

（Ⅰ）当x≥1时，判断H（x）单调性；

（Ⅱ）证明：当x>0时，不等式H（x）>1恒成立.

本题以函数导数知识为载体，以不等式的证明为依托，考查了利用导数求函数的单调性、极值、最值等基本方法，以及分类讨论、数形结合、化归与转化等数学思想.

本题难在第（Ⅱ）问，对于函数不等式的证明，一般有两个思路：①将问题归结为求一个函数的最值解决；②将问题转化为两个函数来解决，用充分性证明.

依据思路1，我们可以得到如下解法1：

证法1：直接求函数f（x）的最值.

以上解答关键是先借助零点存在定理判断出导函数有零点，然后用“虚设零点”的方法设出其零点，最后借助零点表示出原函数的最小值，体现了“设而不求”的策略.

依据思路2，先将函数分离，从待证不等式x2ex-lnx>1出发，可得如下变形：

将以上不等式两边分别看作两个不同的函数，先借助几何画板，在同一坐标系内分别作出其图像，从图形上获取有效信息，再探寻解题方法.

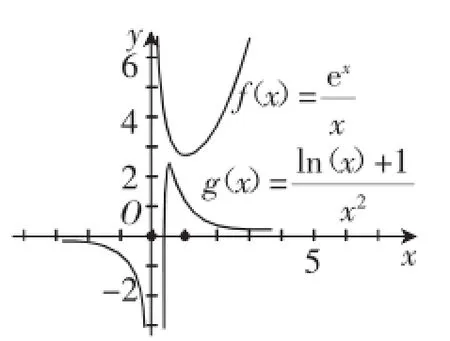
图1　

即f（x）min>g（x）max，故，即原不等式成立.

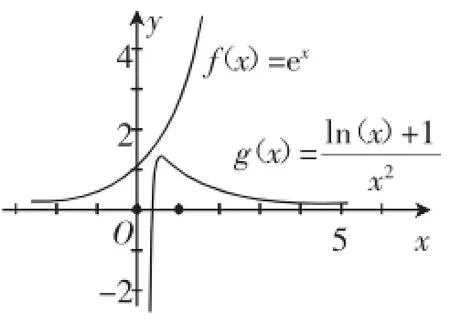
图2　

②由23>e2即ln2>，所以+ln2>1，即则当则g′（x）=，故当时，g′（x）>0，g（x）单调递增；当+∞）时，g′（x）<0，g（x）单调递减.所以g（x）max=g（=则ex>g（x）成立，故原不等式成立.

图3　

证法4：问题等价于证明：x2ex>lnx+1

思路探寻：如图3，g（x）= x2ex的图像在f（x）=lnx+1的上方，f（x）无上界，无法通过最值解决，这时可寻找直线作为中间不等关系转化的桥梁.

不妨令g（x）=x2ex，f（x）= lnx+1.一方面g′（x）=ex（x2+2x），，所以g（x）在处的切线方程为y-，即y=，易证：；另一方面：f（x）=lnx+1在

即问题得证.

图4　

1.649-4×0.693=2.4735-2.772<0，所以H（x）在≈单调递减，所以H（x）>H（1）=

③当x∈［1，+∞）时，f′（x）=（x+1）ex>0，f（x）单调递增，f（x）≥f（1）=e；g′（x）=≤0，g（x）单调递减，g（x）≤g（1）=1.故当x∈［1，+∞）时，（fx）>g（x）.

综上，不等式式成立.

数学离不开图，图是无声的语言，图是思维的起点，图是探究的源泉.从图形中获取有效信息，再回到数学严密的逻辑上去推理论证，是“以形助数”的具体现，值得我们细心体会.Z