聚焦《数系的扩充与复数的引入》中的几类经典问题

■河南省平顶山市一中 李智恒



聚焦《数系的扩充与复数的引入》中的几类经典问题

■河南省平顶山市一中 李智恒

数系的扩充与复数的引入在高考中以容易或中档的小题出现，试题具有活而不难的特点，且常考常新。同学们学习时应狠抓基础，对复数的概念、复数运算等要熟练掌握，还要注意对数形结合思想，复数问题实数化以及方程思想的挖掘和应用。

聚焦一：复数有关概念中的“巧设”和“分类意识”

A.2i B.i C.-i D.-2i

(2)(2015年河北衡水中学调研卷)z1=-4a+1+(2a2+3a)i,z2=2a+(a2+a)i,其中实数a∈R,z1>z2,则a的值是____。

(2)依据两个实数才能比较大小构建方程和不等式组确定参数范围。

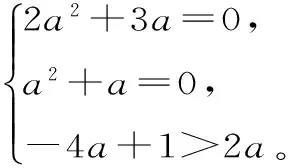
点评：由实数扩充到复数后,实数系的有些性质、运算法则对于复数系并不适用,故解答复数问题时要依据复数的概念合理进行转化，不能轻易地将实数系中的一些运算法则或性质照搬到复数系内。如当两个复数都是实数时,可以比较大小;两个虚数或一个虚数与一个实数不能比较大小。

聚焦二：利用复数相等的充要条件化虚为实

聚焦三：复数运算中的“分母实数化”

解析：分母实数化。

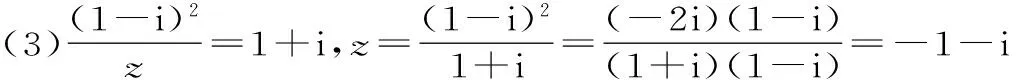
聚焦四：利用共轭复数的性质整体求解复数

当b=0时，z=a，|a-2|=2，则a=0或4。当a=0时不合题意舍去，所以z=4。

当b≠0时，a2+b2=1。

又|z-2|=2，则：

解法2： 利用共轭复数的性质。

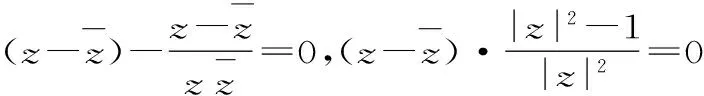
聚焦五：数形结合法探究模的最值

例5 设复数满足||z+4-3i|-2|=2-|z+4-3i|，求|z|的最大值和最小值。

解析：观察分析等式||z+4-3i|-2|=2-|z+4-3i|，根据实数的性质知，若|a|=-a，则a≤0。

因此，|z+4-3i|-2≤0。

图1

挖掘|z+4-3i|-2≤0的几何意义，它表示的以点P(-4，3)为圆心，半径为2的圆及内部。如图1，可知 |z|=|OQ|时，|z|有最大值，|z|max=|OQ|=|OP|+R=5+2=7；

|z|=|OM|时，|z|有最小值，|z|min=|OM|=|OP|-R=5-2=3。

点评：复数既可用代数形式，也可用几何形式表示。这使复数的各种运算都具有了几何意义，因此，求解复数问题时常以形助数，数形结合，使问题的解决更加形象。求复数模的最值常常根据其几何意义，利用图形可直接来解。

聚焦六：用函数与方程思想求模的最值

例6 已知关于x的方程x2+zx+4+3i=0有实数根，求复数z的模的最小值。

点评：复数系方程有实根，不能得出Δ=z2-16-12i≥0，只说明x可以取实数时，复数系一元二次方程不能用判别式来判断方程是否有实根。方程有解的问题要注意系数的范围，当题设条件不特别说明时系数均为复数，处理方程问题的有效途径是巧设代数形式，利用根的意义，借助两个复数相等的充要条件构建方程组，化归到实数中的问题求解。

聚焦七：复数与简易逻辑的网络交汇

例7 (1)(2015年高考上海理科数学)设z1，z2∈C，则“z1、z2中至少有一个数是虚数”是“z1-z2是虚数”的( )。

A．充分不必要条件

B．必要不充分条件

C．充要条件

D．既不充分又不必要条件

(2)(2014年高考陕西卷)原命题为“若z1,z2互为共轭复数，则|z1|=|z2|”，关于其逆命题，否命题，逆否命题真假性对应的判断依次如下，正确的是( )。

A.真，假，真 B.假，假，真

C.真，真，假 D.假，假，假

解析：(1)利用复数概念合理分类研究，借助四种命题之间的关系简化判断。若z1、z2皆是实数，则z1-z2一定不是虚数，因此当z1-z2是虚数时，则“z1、z2中至少有一个数是虚数”成立，即必要性成立；当z1、z2中至少有一个数是虚数，z1-z2不一定是虚数，如z1=z2=i，即充分性不成立，选B。

点评：高考对复数的考查越来越深入，特别是复数与简易逻辑的有机结合应引起同学们的高度重视。复数分类与充要条件的判断，以及对形如a+bi(a，b∈R)的复数的认知，其中a，b分别是它的实部和虚部。若b=0，则a+bi为实数；若b≠0，则a+bi为虚数；若a=0且b≠0，则a+bi为纯虚数。判断命题的真假必须从其定义出发，不可想当然。 互为共轭复数与其模之间的关系构成的四种命题的判断，依据概念只需判断原命题和逆命题的真假即可。

聚焦八：复数与新定义的交汇

①(z1+z2)*z3=(z1*z3)+(z2*z3);

②z1*(z2+z3)=(z1*z2)+(z1*z3)；

③(z1*z2)*z3=z1*(z2*z3);

④z1*z2=z2*z1。

则真命题的个数是( )。

A．4 B．3 C．2 D．1

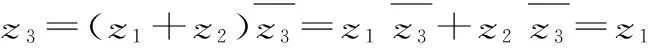
对于②，直接用定义，设复数的代数形式，利用分配律和复数运算结合定义验证：

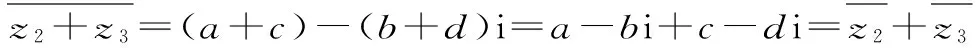
=z1*z2+z1*z3。

故(z1*z2)*z3≠z1*(z2*z3)。

点评：新定义与复数概念运算相结合的创新问题，依据新定义的意义结合复数的概念运算以及运算规律进行验证，涉及复数乘法和加法的结合律和共轭复数的整体性质。

(责任编辑 徐利杰)