高层建筑剪力墙结构中剪力墙合理布置的研究

李炎，王德玲

(长江大学城市建设学院，湖北 荆州 434023)



高层建筑剪力墙结构中剪力墙合理布置的研究

李炎，王德玲

(长江大学城市建设学院，湖北 荆州 434023)

为了合理地在剪力墙结构中布置剪力墙，以使结构更加安全经济，结合实际工程对其结构中剪力墙的布置进行设计调整，得出3种方案，并利用有限元软件SATWE进行建模计算分析。对比方案调整前后的差异探讨不同剪力墙布置方案对结构性能的影响，从而得出合理布置剪力墙的思路和方法。通过加强结构周边剪力墙、翼缘长度以及增加部分剪力墙的翼缘，同时适当减小结构内部部分剪力墙的长度，删除结构内部部分及电梯井筒附近布置较多的墙体，结构的抗侧和抗扭能力能得到有效提高，结构的安全性和稳定性更好。此外还能较大程度上节省材料用量，节约工程成本，可对剪力墙结构设计中结构安全性的提高和工程造价的控制起到一定的指导作用。

高层建筑；剪力墙；合理布置；动力特性；变形特性

剪力墙结构是高层建筑主要结构体系之一，特别是高层住宅结构。但如何合理、经济、有效布置剪力墙是工程设计人员面临的主要问题，也是体现结构师设计水平的重要标志。目前规范对结构中剪力墙的布置没有具体统一的标准，工程设计人员往往根据自己的经验进行布置，可能达不到合理、经济、有效的效果。因此，如何找到一种行之有效的方法做到经济有效布置剪力墙就显得尤为重要。根据实际工程，结合相关规范，采用不同的剪力墙布置方案，通过分析不同结构布置方案下的结构力学性能，得到了更为合理的结构布置方案和原则，对工程设计有一定的实际应用价值。

1 工程实例

1.1 工程概况

荆州市某高层住宅建筑结构体系为纯剪力墙结构，建筑物平面尺寸为37m×23.5m，建筑总面积为15440.36m2，地下1层，地上16 层，标准层层高为2.9m，建筑总高度为46.65m。该工程结构设计使用年限为50年，建筑结构安全等级为二级，剪力墙抗震等级为四级。该地区工程抗震设防烈度为6度，设计基本地震加速度为0.05g，设计地震分组为第一组，建筑场地类别为Ⅱ类，地面粗糙度为B类[1]。

1.2 结构模型的描述

结合剪力墙结构设计的一般规定，对结构中剪力墙的布置进行优化调整：

第一，采用工程原建筑结构施工图的计算模型作为剪力墙的布置方案一；

第二，减小结构的扭转作用，增强结构刚度，按照“连续、周边、对称”的原则，在方案一的基础上加强结构周边剪力墙的布置，即增加周边部分墙体或其翼缘长度，适当增添部分墙体的翼缘，得出方案二；

第三，满足结构安全性的条件下节约工程造价，在方案二的基础上通过减小、删除结构内部部分剪力墙，删除部分电梯井筒附近布置较多的剪力墙，得出方案三。

根据上述3种方案建立3种结构模型，采用有限元软件SATWE进行计算分析，通过对比分析3种结构模型的内力特性、变形特性和动力特性的变化特征，研究剪力墙数量和位置上的变化对结构性能的影响，从而做出剪力墙是否合理布置的判断[1，2]。

结构方案一：采用工程原建筑结构施工图作为剪力墙平面布置图，如图1所示。

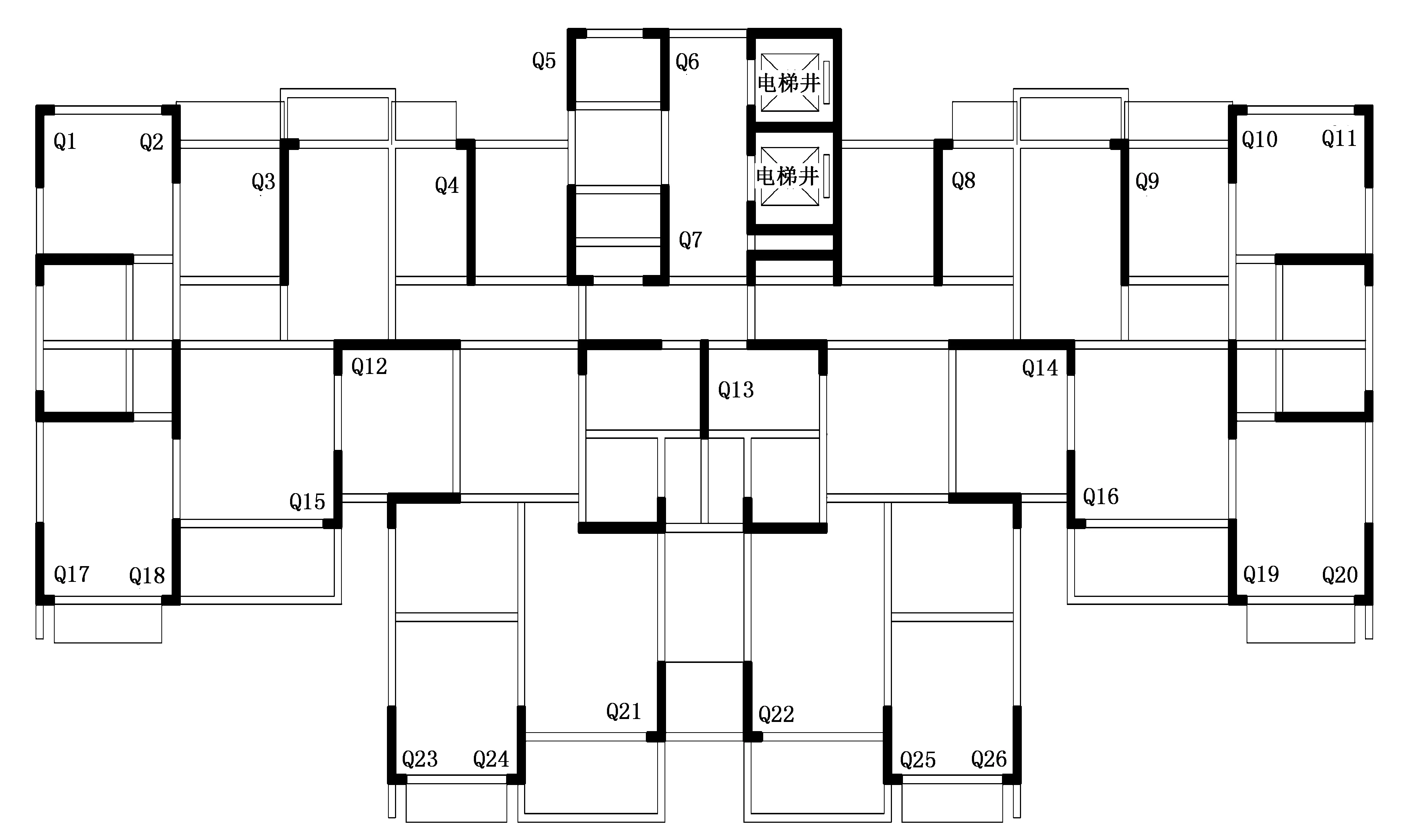
图1 方案一剪力墙平面布置图

结构方案二：对方案一中剪力墙的布置进行调整：①增加结构周边剪力墙长度，即Q1、Q11、Q17、Q20、Q23、Q26剪力墙的长度；②增加Q1、Q2、Q3、Q5、Q9、Q10、Q11、Q15、Q16、Q21、Q22剪力墙的翼缘长度；③增加Q18、Q19、Q24、Q25剪力墙的翼缘。从而得出方案二剪力墙平面布置图，如图2所示。

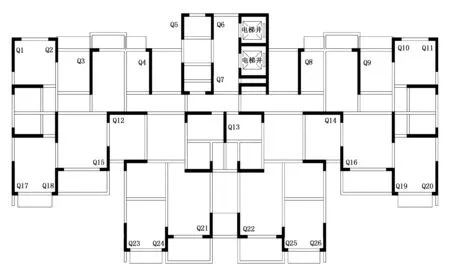
图2 方案二剪力墙平面布置图

结构方案三：进一步对方案二中剪力墙的布置进行调整，删除结构内部部分剪力墙，即删除Q6、Q7、Q13剪力墙；减小结构内部部分剪力墙的长度，即减小Q3、Q4、Q8、Q9、Q12、Q14剪力墙的长度；电梯井筒附近墙体布置较多，删除部分墙体，从而得出方案三剪力墙平面布置图，如图3所示。

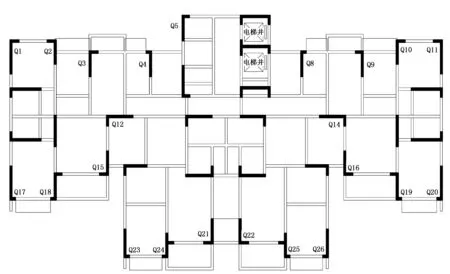
图3 方案三剪力墙平面布置图

2 计算结果的对比分析

根据调整前后3种剪力墙的布置方案，建立3种结构模型，利用有限元分析软件SATWE进行建模计算分析，并对3种模型的内力特性、动力特性、变形特性以及经济性方面进行对比研究。

2.1 动力特性

1)周期 计算结果如表1所示，仅选取前10个振型的周期进行比较研究。

表1 结构振型周期对比表

根据表1中各振型的周期数据，可计算出模型一、模型二和模型三的周期比分别为0.80、0.78和0.75，可以看出三者都在《高层建筑混凝土结构技术规程》第3.4.5条规定的A级高度高层建筑周期比不应大于0.9的范围内，都能够符合要求。从周期比的数值上看，模型二的周期比要比模型一小，周期比越小，结构抗扭作用越大，说明模型二的抗扭转作用要比模型一好，结构的抗扭能力得到了一定提高[2]。此外，模型三的周期比要比模型一、二更小，说明模型三结构的抗扭转效果更好。通过模型一到模型三的结构振型周期比数据的对比分析，可以总结出合理加强结构周边的剪力墙布置，同时适当减弱结构内部剪力墙的作用，可有效地提高结构的抗扭作用，增强结构的稳定性。

同时从表1中各模型的周期数值的比较上可以看出，模型二的周期比模型一的周期都相应要有所减小，说明模型二的刚度与模型一的刚度相比要有所增强，模型二相对于模型一还具有一定的刚度优化效果。加强结构周边剪力墙的布置，可在一定程度上提高结构的刚度和抗扭转能力，对扭转效应较大的结构可起到一定的控制。然而模型三中每个振型所对应的周期相对于模型一、二都要有所增大，说明结构的刚度相对于前2个模型均有所降低，结构变得更“柔”，但三者之间的数值变化幅度不大，结构的刚度变化小，结构仍具有较大刚度。而且方案三的剪力墙布置较前2个方案，在结构仍具有合理刚度的基础上，明显地减少了结构中剪力墙材料的用量，在一定程度上能节约工程成本，有利于造价控制。方案三的剪力墙布置更为合理、经济。

2)振型 根据《高层建筑混凝土结构技术规程》5.1.13条第1款的规定：抗震设计时，宜考虑平扭耦联计算结构的扭转效应，振型数不应小于15，对多塔楼结构的振型数不应小于塔楼数的9倍,且计算振型数应使各振型参与质量之和不小于总质量的90%[3]。根据上述规定，该结构的模型均计算21个振型。从SATWE计算结果中可得，在模型一中，X、Y方向的有效质量系数分别为98.31%和98.25%；在模型二中,X、Y方向的有效质量系数分别为98.30%和98.23%；在模型三中,X、Y方向的有效质量系数分别为98.35%和98.33%。可以看出三者均能够满足规范规定的有效质量系数在90%以上的要求。

对比图4模型一和图5模型二的结构振型图，发现两者均表现出X方向投影振型的摆动曲线分布无序，不规律，而Y方向的摆动曲线分布更均匀，对称且有序，说明在2个模型中Y方向上的结构刚度更好。此外还可看出，模型二在各振型迭加中所表现出的摆动分布相对于模型一更集中化，幅度更小，可大致判断模型二的抗震作用更大，结构的抗震性能更好。说明加强结构周边剪力墙的布置,可在一定程度上改善结构的抗震性能，但从图4和图5中可看出两者摆动分布区别不大，提高效果不明显。

图4 结构振型图(模型一)

'对于图6模型三的振型图，发现与前2个模型振型图的对比结果具有一定相似之处，表现在Y方向的摆动曲线分布要比X方向规律且有序，Y方向上的结构刚度更好。进而说明通过剪力墙布置方案的逐步调整，对结构X、Y方向上的刚度差异调整不大。同时还可看出，模型三前10个迭加振型所表现出的摆动曲线分布差异较前2个模型大，模型三中Y方向的摆动分布更集中于中心线附近，幅度更小，而X方向的摆动幅度更大，但分布相对规则，对称且均匀。根据以上分析可判断模型三的结构布置更规则合理，抗震性能更好，抗震作用更强。

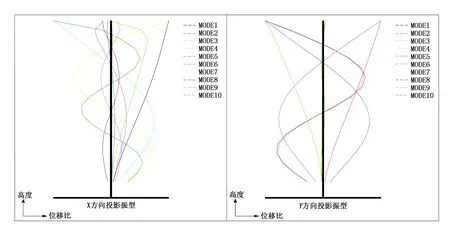
图5 结构振型图(模型二)

对比3个结构模型的振型图，可以发现结构振型图的发展越来越规则、有序，说明通过方案一到方案三对剪力墙布置的优化调整，结构布置的规则性得到进一步提高，结构的抗震作用得到了逐步的优化和加强。相对于前2个方案，方案三布置更规则，结构抗震性能更好。

2.2 变形特性

主要从结构的最大层间位移比和最大层间位移角2个方面进行研究，计算结果统计如表2和表3所示。

从表2中可知，在各工况下模型一的最大层间位移比为1.37，模型二的最大层间位移比为1.32，模型三的最大层间位移比为1.18，均能够满足《高层建筑混凝土结构技术规程》第3.4.5条规定的A级高度高层建筑不宜大于该楼层平均值的1.2倍，不应大于该楼层平均值的1.5倍的要求。在各工况下从各模型的层间位移比上看，模型一到模型三的层间位移比的数值逐渐减小，说明通过方案的逐步调整，结构模型的抗扭转作用得到逐步增强，结构的整体稳定性能更好。从表2中可看出模型三结构的抗扭转能力更强，更有利于结构的整体稳定。

表2 最大层间位移比统计表

表3 最大层间位移角统计表

根据表3中列出的数据可知，各工况下3个模型的最大层间位移角都远小于1/1000，都能够很好地满足《建筑抗震设计规范》表5.5.1规定的剪力墙结构的弹性层间位移角限值为1/1000的要求[4]。表明3个模型的抗侧刚度均较大，抗侧作用强。两两对比而言，模型二相对于模型一的最大层间位移角要小一些，说明结构的抗侧刚度有一定的提高，抗侧作用增强，方案二在方案一的基础上具有一定的抗侧性能优化作用。模型三的最大层间位移角比模型二都要大，表明模型三相对于模型二，结构的抗侧作用相对有所减弱，但从数值上看，模型三在各工况下的最大层间位移角远小于规范规定的限值为1/1000的要求，结构仍具有较大刚度，抗侧作用强。从表3中3个模型在各工况下最大层间位移角的数据的对比上看，从模型一到模型三，数值之间的变化幅度小，结构的侧移刚度变化小，结构均具有良好刚度，抗侧性能好。而对于模型三，结构在具有良好刚度的同时，经济性更好，方案三的剪力墙布置效果相对更为优化。

图7 各模型轴压比统计分布图

2.3 内力特性

主要从结构的轴压比方面进行分析。模型一、模型二和模型三轴压比计算统计结果如下图7所示。

根据图7各模型轴压比统计分布图，可看出模型一、模型二和模型三的轴压比都控制在0.6以内，均能满足《高层建筑混凝土结构技术规程》表7.2.13规定的剪力墙墙肢轴压比限值0.6的要求。

从图7中可得，模型一的轴压比在0.4以下占总数的38.09%, 0.4以上占61.91%，其中0.5～0.6占19.05%。模型二的轴压比在0.4以下占总数的41.49%, 0.4以上占58.51%，其中0.5～0.6占17.02%。可看出两者的轴压比分布情况相差不大，在轴压比0.4以下所占比重均较大，在0.5～0.6之间均较小。说明模型一和模型二的结构安全性强，能很好地满足规范规定的轴压比限值的要求，但也反映出2个模型中存在部分剪力墙没有充分发挥其力学性能，造成了一定的浪费，存在进一步优化的空间。通过增强周边剪力墙的布置，可有效提高结构的抗侧和抗扭刚度，使结构更安全稳定。对于不规则，扭转效应大，受力分布不均匀的剪力墙结构，设计人员可考虑采取加强结构周边剪力墙的布置措施，以改善结构的受力性能，满足结构的安全可靠性[5～9]。但也要同时注意到这一措施增加了结构中剪力墙材料的用量，存在构件材料性能未能得到充分利用的情况，在一定程度上增加了造价成本，不经济。从而对结构中剪力墙的布置还可进行进一步的优化调整，以使结构在满足足够安全的前提下更为经济合理。

根据模型三轴压比统计结果，可看出在该方案中，轴压比在0.4以下的仅占总数的32.96%, 0.4以上占67.04%，其中0.5～0.6占28.41%。与模型一和模型二相比，模型三在轴压比0.4以下所占比重较前两者小，在0.4～0.6之间所占比重大，特别是在0.5～0.6之间最大。表明模型三剪力墙结构的安全性好而且材料性能得到了进一步地充分利用，结构的力学性能发挥的更好，结构布置更加优化合理。

2.4 经济性对比

通过比较3个结构模型的单位用钢量和混凝土用量的统计数据(见表4)，不难发现模型二的含钢量和混凝土用量要大于模型一，模型三的含钢量和混凝土用量最小。

表4 各模型钢筋和混凝土用量统计表

通过加强结构周边剪力墙的布置，模型二消耗的钢筋和混凝土用量比模型一大，从表4中可以得出，钢筋的用量每平方米增加了2.78%，混凝土用量增加了2.89%。虽在一定程度上增加了材料用量，提高了造价成本，但可看出增长幅度较小，而且模型二相对于模型一，结构的抗侧和抗扭刚度得到了明显提高，稳定性增强，优化效果明显。因此对于不规则、扭转效应较大的结构，可采取加强结构周边剪力墙布置这一措施来改善结构的力学性能，提高结构的安全性，此外工程造价的变化幅度不大，可接受。

相对于模型二，模型三的钢筋用量每平方米下降了7.58%，混凝土用量下降了7.39%；相对于原结构模型一，模型三的钢筋用量每平方米下降了5.01%，混凝土用量下降了4.71%。与结构模型一、二相比，可看出模型三的含钢量和混凝土用量最小，其剪力墙布置方案的经济性最好，有利于节约工程造价。同时随着方案的逐步调整，结构模型的力学性能、刚度、安全性逐步得到强化，模型三相对于前2个模型，力学性能更好，安全性、稳定性更强。综上所述可知，方案三的结构布置更为安全经济。

3 结语

1)加强结构周边剪力墙的布置，即增加结构周边剪力墙、翼缘长度以及增加部分剪力墙的翼缘，能有效地提高结构的抗扭刚度和抗侧刚度，增强结构的安全性和稳定性。在剪力墙结构的设计中，对于不规则、扭转效应较大，受力分布不均匀的结构，设计人员可考虑采取加强结构周边剪力墙的布置措施，以改善结构的受力性能，提高结构的安全可靠性。但也要同时注意这一措施增加了结构中剪力墙材料的用量，在一定程度上提高了工程造价，虽造价变化幅度较小，但在满足结构足够安全的基础上,还应进行进一步优化布置剪力墙以使结构更加经济合理。

2)在满足结构安全性的前提下，适当减弱结构内部剪力墙的布置，即减小结构内部部分剪力墙的长度，删除结构内部分及电梯井筒附近布置较多的墙体，能较大程度上节省材料用量，节约工程成本，结构中构件的材料性能能得到充分发挥，结构受力更加合理，经济性更好。此外，虽结构的刚度有一定的削弱，但结构仍具有合理良好的刚度，结构性能的各项指标均能满足现行规范规定的各项要求。

[1]董攀.某复杂小高层住宅结构设计与分析[J].建筑监督检测与造价，2012，5(4):37～39.

[2]胡孔鹏.高层剪力墙结构中剪力墙布置和合理数量的研究[D].合肥：合肥工业大学，2012.

[3] JGJ3-2010，高层建筑混凝土结构技术规程[S].

[4] GB50011-2010，建筑抗震设计规范[S].

[5]胡克楠.高层剪力墙结构中剪力墙布置及合理数量影响因素的研究[D].包头：内蒙古科技大学，2014.

[6]刘哲锋,苏志力,杨伟军.框-剪结构剪力墙布置合理性判别的简化方法[J].建筑结构，2010，40(4)：103～106.

[7]谭方兰.高层住宅结构选型和优化设计[J].建筑结构，2010，40(4)：58～62.

[8]李兆峰,高玉华.高层建筑结构剪力墙布置的合理性探讨[J].工程与建设，2012，26(4)：476～564.

[9]胡庸，贺灵荣.小高层建筑短肢剪力墙结构分析及优化研究[J].工业建筑，2013，S1(43)：243～246.

[编辑] 计飞翔

2016-05-27

国家自然科学基金项目(51408057)。

李炎(1992-)，男，硕士生，现主要从事工程结构设计和工程抗震方面的研究工作；通信作者：王德玲，386841134@qq.com。

TU375

A

1673-1409(2016)25-0055-07

[引著格式]李炎，王德玲.高层建筑剪力墙结构中剪力墙合理布置的研究[J].长江大学学报(自科版)，2016,13(25)：55～61.