一种快速的统计不相关LDA求解算法

谢玉凯，卢桂馥

(安徽工程大学计算机与信息学院，安徽 芜湖 241000)



一种快速的统计不相关LDA求解算法

谢玉凯，卢桂馥

(安徽工程大学计算机与信息学院，安徽 芜湖 241000)

为进一步提高ULDA算法的求解效率，提出了一种新的快速的统计不相关LDA求解算法(ULDA/new)。ULDA/new只需对一个(c-1)×(c-1)的矩阵进行一次特征值分解就可以求得所有的投影向量(c指的是样本量类别数)，从而进一步大幅度地提高了计算效率。理论分析和在图像库上的试验表明，ULDA/new与现有的ULDA求解算法在理论上是等价的，其识别率相同，但远比现有的ULDA算法要高效。

特征提取；线性鉴别分析；统计不相关LDA；QR分解

基于Fisher准则线性鉴别分析(Linear Discriminant Analysis, LDA)[1]是一种经典的特征抽取算法，在模式识别和机器学习领域中有着广泛的应用[2]。LDA算法的基本思想是寻找一组投影向量集，使得原始样本向这组向量集投影后的特征之间的类内的距离最小，而类间的距离最大。

在1975年，Foley等[3]发展了经典的LDA，提出了Sammon最佳鉴别平面的技术，该方法找到的投影向量是相互垂直的。Foley等提出的方法只能用于解决2类问题，进一步的，Duchene等[4]推广了Foley等的方法，并给出了适合于多类问题的正交向量集的求解公式。虽然Foley等和Duchene等的算法求得的投影向量是相互垂直的，但并不能保证得到的特征是统计不相关的，为了解决这一问题，Jin等[5，6]提出了统计不相关LDA(Uncorrelated LDA, ULDA)算法。与Foley等和Duchene等算法求得的投影向量集不同，ULDA算法求得的投影向量集是相互共轭正交的，并且利用ULDA算法得到的特征是统计不相关的。

Jin等虽然在文献[6]中给出了求解统计不相关投影向量集的精确算法，但是需迭代求解，较为复杂，所耗费的计算量较大。当总体散布矩阵非奇异时，Ye等[7，8]证明了ULDA算法求得的投影向量集与传统LDA算法求得的投影向量集是等价的。对于模式识别和机器学习中经常遇到高维小样本问题，由于总体(或类内)散布矩阵往往是奇异的，使得因此Jin等的ULDA算法难以直接计算。因此，Ye等[7]对ULDA算法进行了进一步地推广，使得其能应用于高维小样本问题。通过对3个散度矩阵同时对角化，Ye等提出了一种新的ULDA求解算法(称为ULDA/SVD)，Ye等的求解算法可以一次性地求得所有的投影向量，使得其算法复杂度比Jin等的求解算法有了大幅降低。虽然Ye等的ULDA求解算法可以一次性的求得所有的投影向量，但是其求解算法需进行多次奇异值分解(Singular Value Decomposition, SVD)，与矩阵的QR分解相比，对矩阵进行奇异值分解的效率较低[9]。为此，Chu等[10]提出了一种基于QR分解的ULDA求解算法(称为ULDA/MQR)，使得算法复杂度得到了进一步地降低。但是，Chu等的求解算法需进行多次QR分解。为了进一步地提高计算效率，最近，Chu等[11]提出了一种计算效率更高的ULDA求解算法(称为ULDA/SQR)，该算法只需进行一次QR分解，从而进一步地降低了算法复杂度。对ULDA/SQR算法进行分析可以发现，ULDA/SQR需对所有样本组成的矩阵进行QR分解，使得当样本数较多时，其计算效率仍较低。

为了降低ULDA算法的算法复杂度，笔者设计了一种新的快速的ULDA求解算法(称为ULDA/new)。

1 统计不相关LDA算法

(1)

(2)

=Sb+Sw

(3)

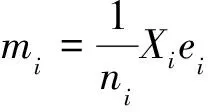
LDA算法的目标函数为：

(4)

式中，G为所有投影向量组成的投影矩阵； trace(▯)表示求矩阵的迹。

(5)

式中， (▯)+表示求矩阵的伪逆。

利用奇异值分解，通过对类内、类间和总体散布矩阵同时对角化，Ye等在文献[7]设计了ULDA的求解算法(称为ULDA/SVD)，其算法复杂度为：

14dn2+4dnc+14nc2-2n3-2c3+O(dn)

为了提高ULDA算法的求解效率，Chu等[10]提出了另一种ULDA的求解算法(称为ULDA/MQR)。ULDA/MQR主要通过QR分解而不是SVD分解来求解投影矩阵，由于当矩阵的大小相同时，QR分解要比SVD分解高效，从而使得ULDA/MQR的算法复杂度比ULDA/SVD的算法复杂度要低。ULDA/MQR的算法复杂度为：

对于高维小样本问题，一般地，有d≫n≫c，因此ULDA/MQR的算法复杂度要低于ULDA/SVD。

最近，Chu等[11]又提出了一种更快的ULDA求解算法(称为ULDA/SQR)。与ULDA/MQR相比，ULDA/SQR只需进行一次QR分解就可以求得投影矩阵，而ULDA/MQR则需进行多次QR分解才能求得最终的投影矩阵，从而进一步提高了ULDA的计算效率。ULDA/SQR的算法复杂度为：

2 新的快速的ULDA求解算法(ULDA/new)

对ULDA/SQR进行分析可知，ULDA/SQR需对所有样本组成的矩阵进行QR分解，使得当样本数较多时，其计算效率仍较低。为了进一步地提高ULDA算法的求解效率，笔者提出一种新的快速的ULDA求解算法，ULDA/new只需对一个(c-1)×(c-1)的矩阵进行一次特征值分解就可以求得最佳投影矩阵G，从而进一步大幅度地提高了计算效率。

(6)

其中， X1∈Rd；X2∈Rd×(c-1)；X3∈Rd×(n-c)。则有：

(7)

HTH=VΣVT

(8)

其中，V∈R(c-1)×(c-1)为特征向量矩阵；Σ∈R(c-1)×(c-1)为特征值矩阵，其特征值从大到小排列，且为对角矩阵。

则G=HVΣ-1即为ULDA的目标函数式(5)的解。

证明 由H的定义，有：

=0

(9)

=0

(10)

由式(10)可以得到：

GTSwG =Σ-1VTHTSwHVΣ-1

=0

(11)

由于：

St=Sb+Sw

(12)

故由式(12)、(11)、(7)和(9)可以得到：

GTStG =GTSbG+GTSwG

=GTSbG

=Σ-1VTHTHHTHVΣ-1

=Σ-1VTVΣVTVΣVTVΣ-1

=Ic-1

(13)

由式(13)可知， 即为ULDA的目标函数式(5)的解。

为了求出G，需先得到H，接下来考虑如何快速地求出H。为了求出H，需先得到X2和X3，而如果直接对式(6)进行矩阵相乘来求解X2和X3，则其算法复杂度为O(dn2)，计算效率较低。由于Wi是Householder矩阵，故其可以表示为：

(14)

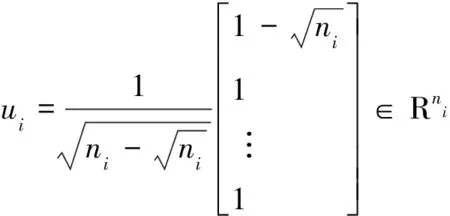
由于：

(15)

而：

(16)

由于P为置换矩阵，因此，只需根据P交换相应的列就可以得到一个矩阵与P的乘积。与式(16)类似，由于W也为Householder矩阵，故一个矩阵与W相乘也可以转化为矩阵与向量的乘积，从而降低算法复杂度。因此，根据式(6)来计算X2和X3的算法复杂度为O(dn)。

(17)

综上所述，笔者提出的ULDA/new总结如下：

输入：数据矩阵X。

输出：投影矩阵G。

1)根据式(6)计算X2和X3；

3)根据式(17)计算H；

4)计算HTH及其相应的特征值分解HTH=VΣVT；

5)计算G=HVΣ-1。

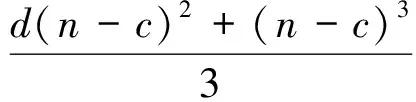
由于对于高维小样本问题，一般地，有d≫n≫c。很明显，和ULDA/SVD，ULDA/MQR和ULDA/SQR求解算法相比，ULDA/new的算法复杂度要低的多。

3 试验分析

为了验证ULDA/new的有效性，笔者在AR人脸图像库进行了试验，编程环境为MATLAB 2008，操作系统为Windows 7，试验中使用的分类器是最近邻分类器。

AR人脸数据库包含126个人(70位男性，56位女性)的4000多张彩色人脸图像，这些图像由不同光照，不同表情和不同的遮挡情况下的正面人脸图像组成。大部分人的图像是在相隔2周的时间下拍摄的2个像集。试验中采用了其中120个人(65位男性，55位女性)的26幅人脸图像，共计3120幅人脸图像，图像处理成120×80的形式。图1为AR人脸图像库中某人的26幅图像。

图1 AR人脸库中的26幅图像

下面比较ULDA/new和ULDA/SVD，ULDS/MQR以及ULDA/SQR等统计不相关LDA求解算法的识别性能。随机在AR人脸库库中选择i(i=7,8)幅图像作为训练样本，剩余的图像作为测试样本。试验重复了20次，结果见表1，表中给出了20次试验的平均识别率和标准方差。从表1可以看出，新的ULDA求解算法ULDA/new与其他几种ULDA求解算法的识别率相同，这也验证ULDA/new与其余几种ULDA求解算法是等价的。

表1 在AR人脸库中不同方法的识别率对比

接下来比较ULDA/new和其他ULDA求解算法的运行时间。表2记录了各种不同ULDA求解算法在AR人脸库上20次所需的平均时间。从表2可以看出，新的ULDA求解算法ULDA/new的运行时间要比其余几种ULDA求解算法要小的多，这与前面的算法复杂度分析是一致的。

表2 不同算法运行时间比较

4 结语

介绍了统计不相关LDA算法，提出了一种快速的统计不相关LDA求解算法。该算法对一个(c-1)×(c-1)的矩阵进行一次特征值分解就可以求得所有的投影向量，大幅度地提高了计算效率。该算法与现有的ULDA算法相比虽然识别率相同，但运行时间上要小的多。

[1]Fisher R A.The use of multiple measurements in taxonomic problems [J].Annals of Eugenics, 1936,7:178～188.

[2] Duda R O, Hart P E, Stork D G. Pattern Classification[M] .2nd ed. John Wiley & Sons, New York, 2000.

[3] Foley D H, Sammon J W J. An optimal set of discriminant vectors [J].IEEE Trans. on Computers, 1975,24 (3):281～289.

[4] Duchene J, Leclercq S. An optimal Transformation for discriminant and principal component analysis [J].IEEE Trans. Pattern Analysis and Machine Intelligence, 1988,10 (6):978～983.

[5] Jin Z, Yang J Y, Tang Z M, et al. A theorem on the uncorrelated optimal discriminant vectors [J], Pattern Recognition, 2001,34 (10):2041～2047.

[6] Jin Z, Yang J Y, Hu Z S, et al. Face recognition based on the uncorrelated discriminant transformation [J].Pattern Recognition, 2001,34 (7):1405～1416.

[7] Ye J.Characterization of a family of algorithms for generalized discriminant analysis on undersampled problems [J].Journal of Machine Learning Research, 2005(6):483～502.

[8] Ye J, Janardan R, Li Q, et al. Feature reduction via generalized uncorrelated linear discriminant analysis [J].IEEE Trans Knowledge and Data Engineering, 2006,18 (10):1312～1322.

[9] Golub G H, Loan C F V. Matrix Computations[M]. 3rd ed. The Johns Hopkins University Press,1996.

[10] Chu D, Goh S T, Hung Y S. Charcterization of all solutions for undersampled uncorrelated linear discriminant analysis problems [J].SIAM J. Matrix Analysis and Applications, 2011,32 (3):820～844.

[11] Chu D, Liao L Z, Ng M K P, et al. Incremental linear discriminant analysis: A fast algorithm and comparisons [J].IEEE Trans on Neural Networks and Learning Systems, 2015,26 (11):2716～2735.

[12] Chu D, Thye G S. A new and fast implementation for null space based linear discriminant analysis [J].Pattern Recognition, 2010,43 (4):1373～1379.

[编辑] 洪云飞

2016-05-17

国家自然科学基金项目(61572033 , 71371012)；安徽高校自然科学研究项目重大项目(KJ2015ZD08)；教育部人文社会科学规划项目(13YJA630098)。

谢玉凯(1990-)，男，硕士生，现主要从事计算机视觉方面的研究工作。

卢桂馥(1976-)，男，博士(后)，副教授，现主要从事人工智能、模式识别方面教学与研究工作；E-mail:luguifu_jsj@163.com。

TP391

A

1673-1409(2016)25-0008-06

[引著格式]谢玉凯，卢桂馥.一种快速的统计不相关LDA求解算法[J].长江大学学报(自科版)，2016,13(25)：8～13.