基于协整 -GARCH模型最优阈值统计套利研究

覃良文，唐国强，林 静

（桂林理工大学理学院，广西　　桂林 541006）

基于协整-GARCH模型最优阈值统计套利研究

覃良文，唐国强，林 静

（桂林理工大学理学院，广西桂林 541006）

依据协整和GARCH模型理论，以历史数据作为样本，建立预测未来标准残差序列的模型。利用GARCH模型标准残差序列预警套利信号，搜索标准残差套利的最优阈值和风险测度，建立最优套利方案。检验结果表明，以历史数据建立的最优套利方案对样本外数据进行套利，与传统利用标准正态分布置信水平确定阈值进行套利相比效果更好，其收益和套利成功率均更高，适用于未来短期跨期套利；最优阈值套利方案量化风险值，可有效控制套利风险，适用于低风险投资爱好者。

最优阈值；风险测度；GARCH模型；跨期套利；最优套利方案

0 引 言

近年来我国兴起了期货跨期套利，跨期套利就是同时反向交易数量相同的不同月份合约，是赚取两个合约价格差额的投资方式。同时，国内针对股指期货的程序化交易研究逐渐兴起。我国的程序化交易就是将原来人工交易的方法转化为计算机的算法程序，用计算机代码识别交易命令［1］。这样的程序化交易没有严密的统计学和金融理论基础支撑，与真正的量化程序化交易存在极大差距。如今，如何利用股指期货在控制风险情况下得到最大套利利润成为广大金融投资者所共同面临的问题。

目前，海内外有诸多学者对股指期货进行跨期套利的研究，其中Machinlay等探究了标准普尔500指数期、现货价格的真实价差是否存在套利机会的情况［2］。何树红等运用GARCH模型建模，拟合预测残差的异方差性，用样本数据预测未来价差变化，然后利用置信度估计套利的建仓、平仓、止损阈值进行套利［3］。赵莉发现沪深股票市场具有异方差的波动特征，适合应用GARCH模型族进行拟合刻画［4］。李世伟改进了协整跨期套利交易方法，将改进套利交易策略运用于沪深300股指期货的套利中，取得较好套利结果［5］。

国内外学者均致力于研究套利机会是否存在和套利模型的建立，然后论证模型可以进行跨期套利，但都存在以下不足：1）不易用 GARCH模型里非正态分布标准化残差序列套利；2）没有考虑套利风险控制问题；3）没有考虑套利收益最优的问题；4）没有考虑收益与承受风险关系。针对上述4个问题，本文利用沪铜期货收盘价数据，应用GARCH模型刻画残差序列的条件异方差性，通过搜索标准残差最优建仓与平仓的阈值以及风险测度建立最优套利方案，使得在相同时间占用同等的资金套利效益最高，套利的成功率较高；通过风险测度对风险进行评估与控制，套利者在选择承受最优的风险值时，套利的效益最高。

1　基于GARCH模型最优阈值套利步骤

1.1协整理论

许多经典预测模型要求时间序列是平稳的才能取得较好的预测效果。但实际中多数时间序列都是非平稳的，只有经过差分后序列才能平稳，但差分后的序列会损失部分有用信息，经典预测模型就不能进行准确预测。为解决上述难题，专家学者经过长期研究，得出处理非平稳时间序列的新理论——协整理论。

协整理论表述为

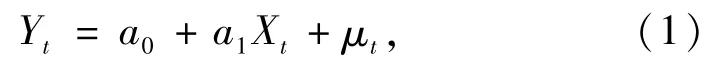
其中：时间序列X、Y均为I（1）序列；非均衡误差μt为I（0）平稳白噪声序列，则说明两时间序列是协整的。具有协整关系的序列具有长时间的均衡关系，可以运用经典回归模型建立回归预测模型，防止产生“伪回归”的情况。

1.2GARCH模型

许多时间序列存在着在某一段时间范围内价格波动剧烈、下一段时间价格波动变得平缓，这是金融序列的集群波动现象。这种情况下的时间序列大多存在异方差的特征：当下时刻的价格条件方差受上一期的方差值影响。GARCH模型能精确刻画具有异方差特征的序列，并且拟合度高、预测效果好。该模型可由下式描述。

均值方程：

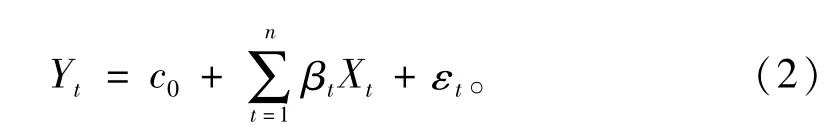
条件方差方程：

残差序列标准化如下：

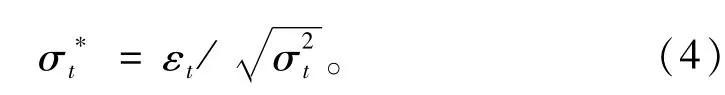
1.3基于GARCH残差的套利交易策略

在两序列满足协整理论前提下，标准化残差具有描述预测期货未来价格走势、预报套利机会的性质。标准化残差序列都近似服从期望为0、方差为1的分布。依据标准残差值的波动特性，标准残差波动偏离正常临界值（阈值）时建仓（同时买入和卖出不同月份合约），其值回落到正常波动范围后平仓（同时卖出和买入不同月份合约）盈利出场；如果建仓后出现实际价差偏离预期目标并超过预期风险，则止损出局；如果标准残差值反向偏离正常临界值并超过预期风险，同样止损出局。

1.4套利阈值

以GARCH模型的标准化残差序列σ*确定套利区间，设定套利建仓阈值为δ1，套利平仓阈值为δ2，其中且为正数。t时刻对应的标准化残差值为在实际交易中，当标准化残差值波动偏离正常临界范围δ1，出现信号预警套利，进行建仓，则套利预警区间为（-∞，-δ1）∪（δ1，+∞），即满足以下不等式时建仓：

建仓后，若标准化残差序列回落到正常波动中心［-δ2，δ2］内平仓，其正常波动范围无套利区间为［-δ2，δ2］，即满足以下不等式时平仓：

1.5套利风险测度与止损信号

在实际交易中，以GARCH模型标准化残差作为风向标对沪铜期货进行跨期套利，存在着亏损的风险。亏损情况有：

亏损情况一：在实际套利过程中，存在沪铜期货两个月实际价差反向偏离预期套利目标的状况，这会给投资者带来亏损；

亏损情况二：以标准残差序列建仓阈值δ1为建仓套利信号，后续残差值存在一定概率波动继续增大偏离建仓阈值，反向偏离预示真实价差反向偏离套利预期目标，则出现亏损。所以有必要对亏损进行衡量与控制。

风险测度：设在t时刻建仓时两份合约的真实期货价差为W，以反向偏离初始价差W的百分比r衡量亏损风险的大小，则r就表示偏离初始价差的程度，以此作为套利的风险测度。

风险衡量指标量化是风险控制的前提。为对风险进行控制，需在套利过程中设定实际结果偏离预期目标的止损信号。建仓后出现亏损且在止损范围内时，持仓等待亏损的减小；在亏损超过预期的止损范围时，平仓止损出局，减少进一步的亏损。

止损信号：设Δw为套利亏损值，则止损信号可表示为

止损信号的设定利于对套利的风险进行控制。风险值的选取不仅关系着投资者所能承受的风险的大小，而且关系着套利资金的占用问题。选择适合的风险值，才能在最低的风险下占用最少的套利资金获得最高的净利润，使得资金回报率最高。

1.6最优套利方案

运用本文设定的基于GARCH模型残差的套利交易方法，用穷举法遍历所有的套利建仓阈值δ1与平仓阈值δ2以及风险测度为r下的所有套利方案，则套利利润最高的方案就是最优套利方案。在最优套利方案中，该方案选用的套利建仓阈值δ1、平仓阈值δ2和风险值r为最优阈值δ*1、δ*2、r*，并以δ*1、δ*2、r*作为标准对样本外数据进行套利，获取高成功率的套利收益，通过样本外数据套利的收益情况评价模型套利优劣。

1.7基于GARCH模型的程序化最优套利步骤

1）在协整理论基础上，检验沪铜期货两个近月合约5 min高频收盘价格序列是否存在长期均衡关系，在满足协整关系情况下检验序列的ARCH效应；

2）在价格序列存在ARCH效应的条件下，运用GARCH模型拟合两个价格序列，得到样本数据的均值方程和条件方差方程；

3）利用拟合后的GARCH模型计算样本数据的标准化残差序列；

4）利用标准化残差的性质寻找搜索样本数据的最优套利方案，得到样本数据内的最优套利建仓平仓阈值与最优风险测度；

5）以样本内数据的均值方程和条件方差方程预测估计样本外的残差序列，运用相同的套利方法，以最优套利建仓、平仓阈值与风险测度对样本外数据进行套利；

6）数据和模型定期进行更新优化。

2　基于GARCH模型的最优套利的计算与检验

2.1数据来源

选取上海沪铜期货合约CU1504（主力合约）与CU1505（次主力合约）在2014-11-26—12-25一个月时间的5 min收盘价的高频交易数据进行套利研究，总计2 040个数据。其中，2014-11-26—12-17（总计19 d）为样本内数据，2014-12-18—25（总计7 d）为样本外数据。数据来源于文华财经的大有期货交易软件。

2.2计算样本标准化残差序列

2.2.1协整检验 序列相关性分析：用EVIEWS软件计算两序列的相关系数，求得两序列的相关系数为0.998 994，非常接近完全正相关。因此，两序列有很大的概率具有协整关系。

序列平稳性检验：在进行协整关系检验之前，先采用ADF法检验原序列和一阶差分序列的平稳性，结果见表1。

可知，CU1501和CU1502两序列在10%的显著水平下仍不平稳，但它们的一阶差分在1%的显著水平下是平稳的，即两序列都是一阶单整I（1），满足协整检验单整阶相同的要求。

采用EVIEWS软件中的Engle-Granger两步检验法对序列CU1504和CU1505进行协整检验。

（1）对上述OLS方程系数进行估计，均衡关系方程结果如下：

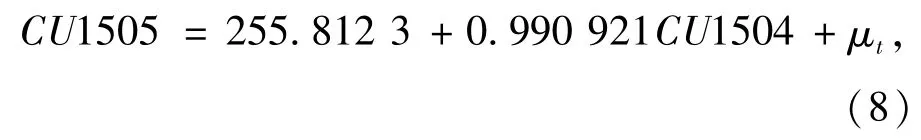
其中，R2为0.997 990，F-statistics为734 737.8。因此，可以认为OLS方程拟合效果很好。

（2）检验均衡关系方程的残差序列的单整性。利用EVIEWS软件，对上述估计得到的OLS方程生成模型估计的非均衡误差序列，记为Resid01。对非均衡误差序列Resid01进行ADF单位根检验（表2）。

根据表2中的结果，非均衡误差Resid01是I（0）平稳序列。根据协整分析理论，沪铜CU1504和CU1505价格序列之间存在协整关系。

2.2.2ARCH效应检验 采用EVIEWS软件，对非均衡误差序列Resid 0l进行ARCH-LM检验，滞后阶数取10，结果如下表3。

表1　序列平稳性检验结果Table 1 Test results of stationary sequences

表2　非均衡误差平稳性检验结果Table 2 Test results of residual stability

表3　Resid 01的　ARCH效应检验结果Table 3 ARCH effect test results of Resid01

因此，拒绝“非均衡误差序列直到10阶都不存在ARCH效应”的原假设，即认为非均衡误差序列Resid0l存在条件异方差性。

2.2.3GARCH模型的构建 通过ARCH-LM检验后，在非均衡误差序列存在ARCH效应的前提下，使用GARCH（1，1）模型来刻画非均衡误差序列的条件异方差性，结果如下：均值方程

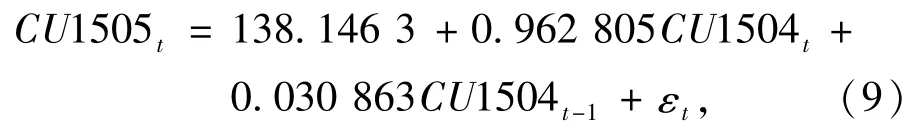
条件方差方程

模型拟合效果较好，满足了以下3个要求：所有系数参数均是显著的；条件方差方程非负数要求；GARCH项和其系数和小于1的约束条件。此外，相关系数R2=0.997 8，非常接近1，说明模型拟合效果较好。

记GARCH模型的残差序列为Resid02，条件方差序列为Garch01。经检验，序列Resid02是平稳序列，且不存在ARCH效应，这也说明GARCH模型的拟合效果较好。

标准化残差序列Resid03为

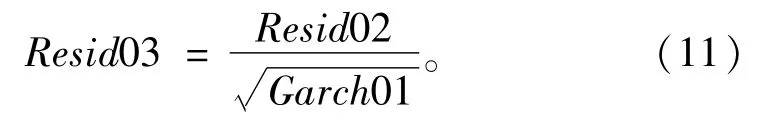
通过EVIEWS软件，得到标准化残差序列Resid03的相关统计量如表4所示。

由表2可知，标准化残差序列Resid03拒绝原假设，即Resid03不服从标准正态分布。

2.3最优阈值套利的详细设计

用计算机编程，先固定风险值r，把标准化残差序列Resid03赋值给σ*，用穷举法循环以0.01为精度遍历［0，4］的所有δ1、δ2。①在t时刻，若σ*

t在套利区间［δ1，+∞］内且未建仓，牛市建仓，买入近期CU1504合约，卖出远期合约CU1505，t=t+1跳入第④步；②在t时刻，若σ*

t在套利区间［-∞，-δ1］内且未建仓，熊市建仓，买入远期合约CU1505，卖出近期合约CU1504，t=t+1跳入第⑤步；③在t时刻，若σ*

t在无套利区间［-δ1，δ1］内且未建仓，t=t+1跳入第①步；④若σ*

t+1落入无套利区间［-δ2，δ2］，两份合约同时平仓盈利出场，计算盈利值，执行第⑥步；

若亏损值Δw落入牛市止损区间［W×r，+∞］，两份合约同时平仓亏损出局，计算亏损值，执行步骤⑥；否则t=t+1继续执行步骤④；⑤若σ*

t+1落入无套利区间［-δ2，δ2］，两份合约同时平仓盈利出场，计算盈利值，执行⑥；若亏损值Δw落入熊市止损区间［W×r，+∞］，两份合约同时平仓亏损出局，计算亏损值，执行⑥；否则t=t+1，继续执行步骤⑤；

⑥计算总的盈利值与亏损值，净利润等于总盈利值减去总亏损值；循环执行上述步骤，直到找到最大净利润与最优套利阈值δ*1、δ*2；

最终，用同样的方法循环遍历所有的风险测度r，搜索到全局最优套利建仓阈值δ*1、平仓阈值δ*2以及风险测度r*。

2.4结果分析与方案检验

上海期货交易所于2014年11月26日公布了阴极铜标准合约的交易手续费：成交金额为0.025‰。阴极铜标准合约报价单位为元/t，交易单位为5 t/手。

表4　Resid 03的相关统计量Table 4 Related statistics of Resid 03

2.4.1样本最优套利模型结果 经过计算机计算，以样本内数据建立最优阈值套利模型，不同阈值与套利总次数（建仓、平仓和止损3种操作次数总和）结果见表5。

最优套利方案中，其中建仓371次，盈利平仓323次，48次止损（最后一次建仓没有平仓）；扣除手续费，单次套利最大净利润688.82元；止损过程中，出现亏损最大为-61.26元，套利风险较低；最优套利模型在样本数据内套利成功率较高，模型在样本中效果非常好。

在样本数据内，扣除操作的手续费后，通过最优套利模型得到建仓阈值、平仓阈值变化与最大净利润的三维坐标关系（图1），套利阈值与套利净利润垂直视角图如图2（颜色深浅代表最大净利润的大小，其中固定风险测度为55%）。

由图1可知，阈值选取与最大净利润关系密切，顶峰存在且唯一，最优建仓阈值与平仓阈值对应最高净利润值；图2颜色较深部分是最大净利润区域，最大净利润区域比较集中，集群现象突显出本套利模型对样本外数据套利有较高的成功率，同时净利润有极大概率落入最大净利润区域。

随着风险测度变化，样本内套利净利润与风险测度变化关系如图3。在样本内最优套利方案中，单次套利净利润变化如图4。

图3显示，样本内数据，不愿承担任何风险的套利净利润值较低；当风险测度达到54%后，最大净利润固定；本文风险测度是表示偏离初始沪铜真实价差的测度，在样本数据内，真实价差的均值是156.57元，单次套利面临最大亏损的金额在241元上下浮动，说明利用本模型的套利投资者有较低风险、亏损额度小的优势。

图4显示，颜色的深浅表示套利操作次数的多少，不同的阈值与套利操作的总次数有着明显的区别；也反映了最高净利润与套利次数没有明显关系，大致处于颜色较浅区域，属于全局套利总次数偏低位置。

2.4.2最优套利方案检验结果 结合样本建立的GARCH模型，将样本外数据代入条件方差方程式（9）与残差方程式（10）预测其标准残差序列，并以样本数据建立最优套利方案：0.34为最优建仓阈值，0.53为最优平仓阈值，54%为最优套利风险值对样本外数据进行套利，结果见表5。

图5、6显示，在样本内数据单次套利中，都已扣除当次操作的手续费，最大盈利值为688.82元，其中多次小额亏损是建仓手续费；样本外单次套利最大盈利值为588.70元，最大亏损值为-11.42元；以最优套利模型进行套利，操作的手续费是制约套利利润的一个重要因素。

表5　样本最优套利方案结果Table 5 Results of sample optimal arbitrage scheme

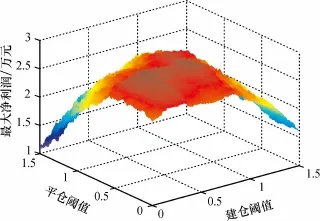
图1　阈值与净利润三维关系图Fig.1 Threshold and profit three-dimensional diagram

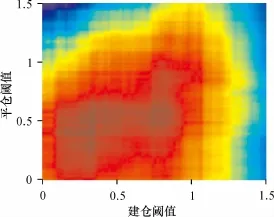
图2　阈值与净利润关系的垂直视角图Fig.2 Vertical view of the relationship between threshold and profit

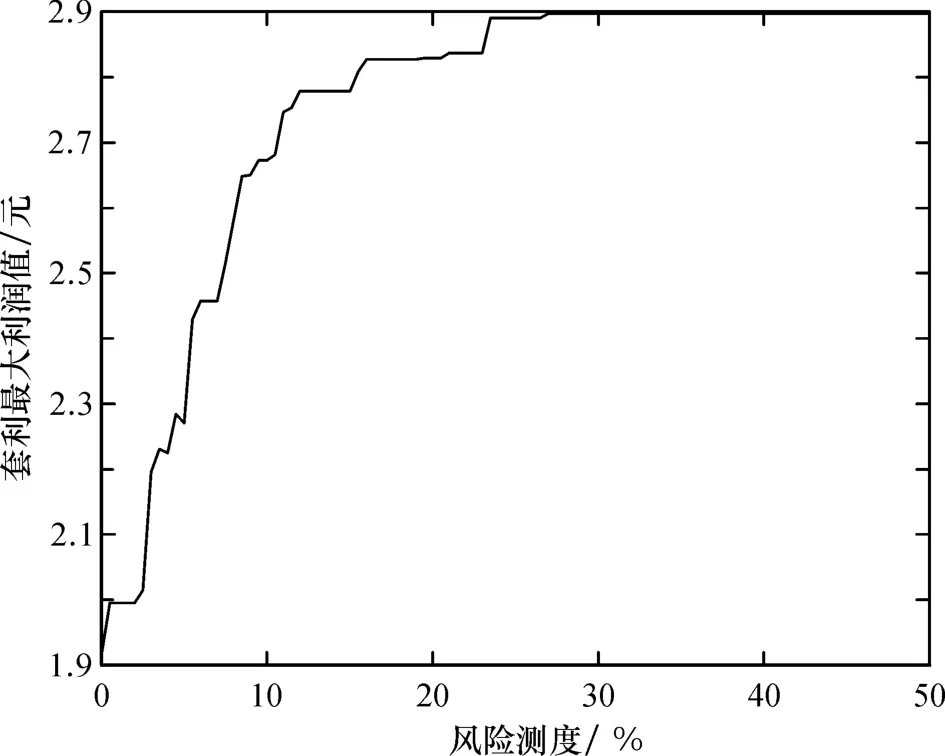
图3　样本最大净利润与风险测度关系图Fig.3 Sample maximum profit and risk measure diagram

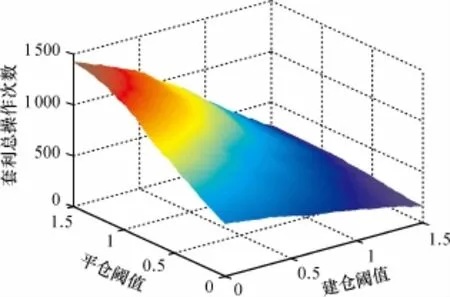
图4　样本内套利总次数与阈值关系图Fig.4 Total number of samples in arbitrage and threshold diagram

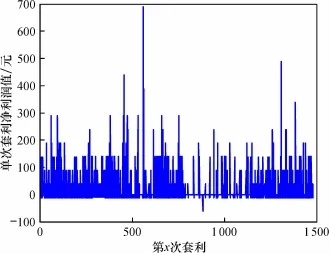
图5　样本内单次套利净利润变化图Fig.5 Sample single arbitrage profit change chart

样本内、外套利结果如表6。可以看出，样本内数据建立的最优套利模型对样本外数据进行套利，成功率与收益较高，二手合约平均每日收益接近1 000元。其中样本外套利成功率高达98.27%，说明最优套利方案套利效果较好，能够用于沪铜期货实际套利交易。

图6　样本外单次套利净利润变化图Fig.6 The out of somple single arbitrage profit charge chart

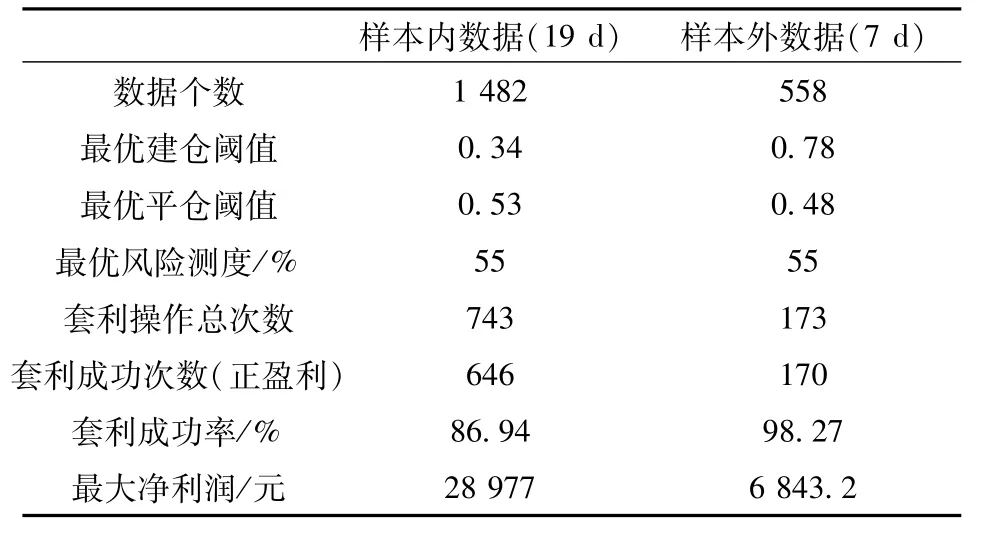
表6　套利检验结果表Table 6 Results of arbitrage test

以样本内数据建立的最优套利方案，适用于未来短期套利且收益较高。基于GARCH的最优套利模型，比传统利用标准正态分布置信水平确定阈值进行套利成功率高，净利润比传统模型高出几倍。模型使用过程中，需不定期更新数据，修正模型，保持模型套利的成功率。建议投资者使用3周连续样本数据建立预测模型，预测时间不超过1周；定期更新样本，建议每周更新一次。

3　结 论

本文在上海沪铜期货两个近月合约指数满足协整理论的基础上，应用GARCH（1，1）模型描述两合约的时变方差，建立最优阈值套利模型。经过检验，以样本内数据搜索寻找最优套利阈值和风险测度建立最优套利方案，适用于GARCH模型里正态和非正态分布标准残差序列的套利，且该方案对样本外数据套利效果良好，风险低、成功率高，能为投资者带来显著的收益，适用于低风险投资者。

［1］王垚鑫.沪深300股指期货程序化交易模型设计［D］.成都：西南财经大学，2013.

［2］MacKinlay A C，Ramaswamy K.Index-futures arbitrage and the behavior of stock index future prices［J］.Review of Financial Studies，1988，1（2）：137-158.

［3］何树红，张月秋，张文.基于GARCH模型的股指期货协整跨期套利实证研究［J］.数学的实践与认识，2013，43（20）：274-279.

［4］赵莉.基于GARCH模型的沪深300指数收益率波动性分析 ［D］.成都：成都理工大学，2012.

［5］李世伟.基于协整理论的沪深300股指期货跨期套利研究［J］.中国计量学院学报，2011，22（2）：198-202.

［6］谢佳新.豆油和棕榈油程序化套利交易模型实证研究［D］.长沙：中南大学，2013.

［7］钟磊.股指跨期套利的程序化策略研究［J］.时代金融，2011（3）：109.

［8］魏武兄.时间序列分析 ［M］.北京：中国人民大学出版社，2010（2）：345-359.

［9］张晓峒.Eviews使用指南与案例［M］.北京：机械工业出版社，2007：137-145.

［10］覃良文，唐国强，林静.基于HP滤波和协整理论的期货套利研究［J］.湖北大学学报：自然科学版，2015，37（6）：570-576.

Statistical arbitrage based on GARCH model and the optimal threshold cointegration theory

QIN Liang-wen，TANG Guo-qiang，LIN Jing
（College of Science，Guilin University of Technology，Guilin 541006，China）

The prediction model is established to predict future standard residual sequence based on cointegration theory and GARCH model，using historical data as samples.GARCH model standard residual serial is used as warning signal to arbitrage in search for optimal threshold and measure of risk in standard residual serial to establish the optimal arbitrage scheme.The results show that the optimal arbitrage scheme established by historical data is good for arbitraging and better than the traditional probability level of the standard normal distribution to determine the threshold.The earnings and arbitrage success rate are suitable for future short-term arbitrage. The optimal arbitrage scheme could quantify the risk and easy to control the risk of arbitrage，especially for low risk investors.

the optimal threshold；risk measure；GARCH model；intertemporal arbitrage；optimal arbitrage scheme

F201

A

1674-9057（2016）03-0625-07

10.3969/j.issn.1674-9057.2016.03.034

2015-03-16

国家社会科学基金项目（13CJY075）；广西财经学院数量经济学自治区级重点实验室建设2014年项目

覃良文 （1991—），男，硕士，研究方向：金融统计，qliangwen@163.com。

唐国强，博士，副教授，tanggq@glut.edu.cn。

引文格式：覃良文，唐国强，林静.基于协整-GARCH模型最优阈值统计套利研究［J］.桂林理工大学学报，2016，36（3）：625-631.