圆形明亮琢型钻石切磨比例的探讨
俞鑫源,阮青锋,俞渊铭,宋 林,杨 杨,张 诗
(1.桂林理工大学 地球科学学院,广西桂林 541004;2.厦门大学经济学院,福建 厦门 361005)
圆形明亮琢型钻石切磨比例的探讨
俞鑫源1,阮青锋1,俞渊铭2,宋 林1,杨 杨1,张 诗1
(1.桂林理工大学地球科学学院,广西桂林 541004;2.厦门大学经济学院,福建厦门 361005)
利用MATLAB软件模拟钻石内部的光路,选取平行等距的光源分别从冠部及亭部照射钻石,重点研究光源从垂直入射至倾斜入射下不同的切工比例对钻石亮度及火彩的影响,从光线返回值、暗区比值和加权平均色散角等方面分析探讨了影响圆形明亮琢型钻石亮度及火彩的各种因素,给出了达到最佳加工效果的各种因素间搭配关系。模拟分析认为:亭角在39.0°~41.0°范围内较为合适,具有最大光线返回值及较小的暗区比值。通过加权平均色散角计算分析,当亭角的大小一定时,存在唯一大小的冠角使加权平均色散角出现明显的峰值,从而获得能够出现最佳火彩效果的亭角与冠角的组合。当钻石的台宽比大于最小台宽比(Amin)时,台宽比对亮度无影响;在Amin~100%范围内,台宽比越小,加权平均色散角的权数越大,火彩效果越好。
钻石;圆形明亮琢型;亮度;火彩;计算机模拟
0 引 言
钻石是目前已知自然产出的硬度最大的宝石矿物材料,具有很高的折射率和色散值。钻石原石看上去朴实无华,但通过良好的切磨与抛光就能使钻石完全展现出其内在璀璨夺目的光彩,这种光彩就是通常所说的明亮度(brilliance),包括亮度(brightness)、火彩(fire)及闪烁(sparkle)三大要素[1]。
钻石的琢型及各部分的比例和角度的差异将会显著地影响钻石的明亮度。早期的琢型只是简单的将钻石八面体原石进行打磨抛光,其明亮度是较差的,尤其是钻石的火彩和闪烁无法体现出来。随着人类社会的进步和科技的发展,钻石的加工技术不断完善,经过漫长的演化历程,才逐步形成了拥有34个小面的老式圆形明亮琢型[2]。20世纪以来,钻石的加工技术飞速发展,钻石琢型也在不断改进,世界各地陆续涌现出具有重大影响的琢型,1916年出现了与现代圆形明亮琢型相接近的圆多面体钻石琢型,其冠角为35°、亭角41°、台宽比为40%,这种琢型已经明显的改善了成品钻石的明亮度,尤其是其火彩和闪烁得到了显著的提高。1919年托尔科夫斯基(Tolkowsky)利用光学原理计算得出了钻石加工发展历程中具有里程碑意义的美国理想琢型[3];1940年德国爱普洛(Eppler)提出了欧洲琢型;1969年出现了斯堪的那维亚(Scan D N)琢型,使圆形明亮琢型钻石的明亮度逐步有了提高;1977年日本人Shigetomi提出的具有八心八箭效应的钻石切磨比例,可以说是到目前为止比较理想的钻石圆形明亮琢型。由于出现了多种不同切磨比例的钻石圆形明亮琢型,对钻石的分级标准也就出现了一些差异,因此,国际钻石委员会(IDC)在综合各种圆形明亮琢型特点的基础上,于1978年公布了理想圆形明亮琢型的比例范围。中国也在1993年推出了自己的钻石分级标准,2010年又对该标准作了进一步的改进[4],明确规定了圆形明亮琢型的理想比例范围(图1),其中,图1a是圆形明亮琢型的纵剖面示意图,冠角的大小以α表示,亭角的大小为β;台宽比是指钻石冠部台面的最大直径与腰部最大直径的比值,用A表示;冠高比为台面至腰平面距离与腰部最大直径的比值;亭深比为腰平面至底尖距离与腰部最大直径的比值。
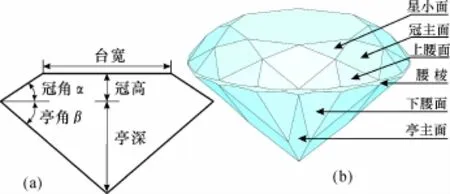
图1 圆形明亮琢型钻石的各部分比例(a)及名称(b)Fig.1 Proportion(a)and form name(b)of the round brilliant cut diamond
钻石的亮度主要取决于两个方面:①钻石冠部刻面的反光强度;②钻石亭部刻面全内反射并从冠部折射出来的光的强度。平整的刻面及精良的抛光能够减少钻石表面的漫反射,达到较好的表面反射效果;而亭部刻面全内反射的光量则由切磨角度所决定。白色光是由400~700 nm的连续光谱色组成的复合光,当白色光在钻石中折射时,由于不同波长的光折射率的微小差异而导致白色光分解为组成它的各种波长的单色光的现象称为色散,不同的单色光从钻石折射进入空气中的角度是不同的,其差值越大越容易被眼睛观察到,即色散(火彩)的效果越好。当钻石转动时,其冠部和亭部刻面所出现的明暗变化及不同色光交替的现象称为闪烁,闪烁度取决于琢型的刻面数量、火彩的强弱以及在观察时钻石转动的速率等因素,实质上与钻石的琢型及切工质量密切相关。因此,切工质量是钻石质量评价体系中的重要指标。而钻石的美观程度又主要由亮度、火彩及闪烁度等具体要素体现出来。所以,对钻石切工质量的评价,除了要考虑钻石琢型加工的精确度和修饰度外,钻石的亮度、火彩及闪烁程度是不容忽视的因素。然而钻石的明亮度与冠角、亭角及台宽比之间的关系十分复杂,某些不同的比例搭配可以产生比较好的明亮度[5]。如何系统全面地评价切工的质量一直困扰着业内人士,在不同的国家和地区,对钻石切工的评价标准都不太一致,因此,切工的质量分级在钻石4C分级体系中也是最具争议的。美国宝石学院(GIA)的研究人员发现,虽然钻石的每个刻面都对其外观产生影响,但钻石的整体外观主要还是由各部分比例的综合因素所决定[6]。只有综合考虑各个刻面之间的比例及相互影响,才能合理评价钻石的整体效果。随着计算机技术的不断发展,繁琐的数学计算已可以由计算机来精确地完成,并可以借助计算机模拟来直观的展示各种不同的情况。本文在前人研究的基础上,利用MATLAB软件建模,分析探讨了光线返回值、暗区比值和加权平均色散角等因素对钻石亮度与火彩的影响,并对几种流行的、不同切磨比例的圆形明亮琢型钻石的亮度及火彩进行了定量分析和计算,为进一步改善现代圆形明亮琢型的明亮度及切工质量分级提供依据。
1 模型的建立
影响圆形明亮琢型钻石明亮度的因素较多,除亮度、火彩和闪烁程度等主要因素外,钻石的反射率(R)、内部细微包裹体对光的反射、折射、吸收及钻石本身对光的吸收等都会影响琢型钻石的明亮度。因此,本次研究主要是针对影响钻石明亮度的主要因素——钻石的切磨比例及角度来开展,同时假设钻石表面具有理想化的抛光程度。一个好的琢型,从冠部进入钻石内部的光线既要尽可能多的返回冠部,又能比较均匀的分布在整个钻石的冠部,从而使钻石看上去更加明亮;对于火彩,发生色散时红光与紫光分开的角度越大,那么色散也就越明显,即火彩越强。基于上述考虑,本次研究主要从三方面着手:①入射光最大限度返回钻石冠部的角度范围;②返回光线能在钻石冠部均匀分布的角度范围;③出现最佳火彩的角度范围。
MATLAB具有强大的数值计算功能,且无需事先对变量赋值,计算结果以标准的符号形式表达;还可以将不同的计算数据以二维、三维乃至四维图形的形式直观地表现出来,这不仅使数据间的关系更加清晰、明了,而且对于揭示钻石比例与亮度及火彩的关系有着非常重要的作用。虽然光线在琢型钻石内部传播的情况比较复杂,但借助MATLAB强大的计算及绘图功能可以精准地模拟不同切磨比例和角度的琢型钻石中光线的传播情况。
1.1变量及参数设置


由于不同切磨比例下返回的光线在冠部表面的分布情况不同,当入射光的角度不合适时必然会在钻石冠部出现比较暗淡的区域,暗淡区域的大小对钻石明亮度将产生重要影响。将钻石冠部投射到圆形明亮琢型钻石的腰部平面上,暗淡区域在腰平面上的投影面积为S暗,其与钻石腰部面积S总的比值定义为暗区比值SD,其表达式为暗区比值就成为评价琢型钻石明亮度的另一个重要指标。

根据前人的研究,钻石的台宽比(A)、亭角(β)和冠角(α)的大小对钻石的明亮度都有不同程度的影响。在模拟计算中,为了更好地反映台宽比、冠角和亭角的变化对钻石明亮度的影响,台宽比(A)的取值范围为0~100%,冠角(α)与亭角(β)的取值范围均为0°~90°,精确到小数点后一位。
1.2光源的选择
在实际情况中,进入钻石内部的光源是随机且复杂的,可能是来自各个不同方向,数量巨大且强度不均匀。考虑到钻石本身的折射率值以及现代圆形明亮琢型的冠角和亭角的大小范围,通过钻石全内反射再从冠部折射出来的光线,绝大多数都是从冠部进入钻石内部的光线,从其他部位进入钻石内部的光线几乎很少从琢型钻石的冠部射出。因此,为了简化,本次选取的光源为1 000条平行且强度均匀的白光。
1.3光路模拟
对于垂直台面入射的任一条光线都能在圆形明亮琢型的钻石上找到一个直径截面,光路的模拟可以在平面内解决。使用MATLAB在平面直角坐标系内取5条直线作为钻石的五边形截面,冠部两条直线及亭部两条直线斜率的改变即为角度的改变。1 000条平行、等距且等向的向量为光源,当光线与钻石刻面相交时,根据斯涅尔折射定律计算光(向量)每次改变后的方向及位置,直到光射出钻石。筛选最终射出的光线中方向向上的光线,并计算每条出射光线与钻石的交点。根据这种思路编写模拟光路的流程图(图2)。最后通过随机抽取样本点的方式,导出光路图,并对MATLAB程序进行反复验证与修正。
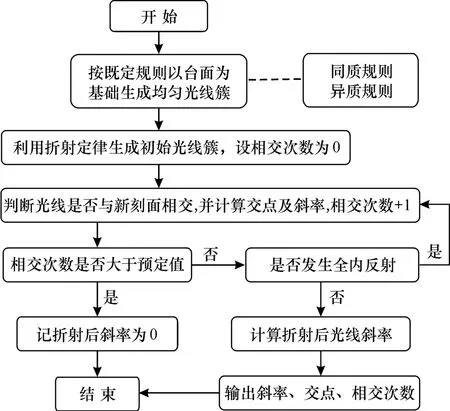
图2 光路模拟流程图Fig.2 Flow chart of the optical path simulation
2 结果与讨论
2.1亮度分析
光线可以从钻石的冠部、亭部和侧面等不同部位进入钻石内部,从侧面进入钻石内部的光线几乎全部从侧面漏出,很难从钻石冠部向上射出,因此,主要是考虑从冠部入射和从亭部入射进入钻石内部的光线情况。
根据光线在不同密度媒介中发生折射和全内反射的原理,当光线从钻石冠部入射,又顺利从冠部射出的几何路径如图3所示。光线从A点垂直台面入射时,光线沿直线方向前行,并在B点与亭部刻面相交,光线将在亭部发生第1次全内反射。从图3不难看出,光线AB与亭部刻面法线的夹角大小必为β,只有满足β大于钻石的临界角i,即
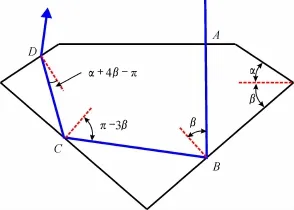
图3 光线顺利返回的角度示意图Fig.3 Angle sketch of the light returning

才能使光线AB在钻石亭部发生全内反射,并沿BC方向到达C点与亭部另一侧的刻面相交,光线BC与过C点的刻面法线的夹角大小为π-3β,只有满足π-3β>i,即

才能使光线BC在C点发生第2次全内反射,使光线沿CD方向到达冠部D点处,此时,光线CD与过D点的刻面法线的夹角大小为α+4β-π,当(α+ 4β-π)<i时,光线CD就能从C点折射出来返回人的眼睛,即满足
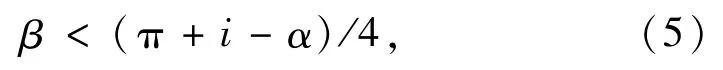
由式(3)~(5)可知,亭角β在0.0°~90.0°的范围内变化时,主要出现4种情况:①β在0.0°~24.4°时,出现第1次漏光(图4a);②β在24.4°~51.1°时,光线能顺利的从冠部射出(图4b);③β在51.1°~51.8°时,光线在亭部两次全内反射至冠部再一次全内反射从而弹回宝石内部,无法顺利折射出来(图4c);④β在51.8°~90.0°范围时,光线发生一次全内反射至另一侧亭部时折射出去发生漏光(图4d)。但是当亭角及冠角发生改变时,光线与冠部的交点也会发生改变,这种简单的数学推导并不能准确地知道每条光线到达的具体位置,每个大的范围内有着更多复杂的光路情况。
为了探明光源照射不同部位时钻石亮度的差异,本次研究分别模拟了光源从冠部及亭部照射的两种情况并利用式(1)计算光线返回值(φ)。当光源从冠部照射时,不同亭角及冠角对应的光线返回值的等高线图见图5。光线返回值超过0.90的区域有两个,左侧区域中冠角的范围为0.1°~48.1°,远远大于亭角37.8°~51.0°的范围。在亭角合适且一定的情况下,冠角的变化对光线返回值的影响不大,因为总有一部分光线能从台面射出,要想达到最大的光线返回值,冠角必须满足不等式(5),否则光线会在钻石内部弹射。然而在冠角一定的情况下,光线返回值随着亭角的改变发生急剧的变化,可见在不同切磨比例的钻石中,亭角的大小是光线能否顺利返回冠部的最重要因素。光线返回值达到1.0的区域有两个(图6):第一个区域的亭角为68.2°~70.0°,冠角为0°~9.1°,显然,这种琢型的亭深太大、冠高太小,整个琢型的比例很不协调,而且无法镶嵌,因而无法被钻石琢型的设计者和加工者采纳;另一个区域所对应的亭角范围为39.1°~51.0°,冠角为0.1°~43.2°,现代圆形明亮琢型的切磨角度被包含在这个范围内。
当光源从亭部照射时,光线返回值(φ)等高线图见图7。当亭角超过39.7°时,φ值急剧下降,这是因为从亭部进入钻石内部的光线绝大部分在到达台面时发生了全内反射又返回亭部折射出来;当亭角小于39.7°时,某些区域可达到较高的光线返回值,但根据对光路的模拟,这些光集中在冠部且向两侧发散,台面黑暗。当钻石被镶嵌后,亭部下方被遮挡,即使亭部可以接收到光也是来自两侧的光。当修改模型中入射光源的方向,使光源与竖直方向的夹角从0°~90°变化时,无论入射光源的角度如何变化,现代圆形明亮琢型的钻石都只有少量的光线向上射出,并且这部分光线的斜率非常低,即向两侧发散,对钻石明亮度基本没有贡献。可见,钻石的亮度主要取决于来自冠部的入射光源,从亭部进入钻石内部的光对钻石的亮度几乎没有影响。
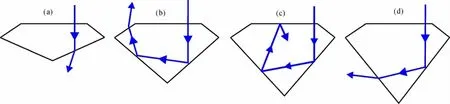
图4 不同亭角范围的光路Fig.4 Light path of different pavilion angles
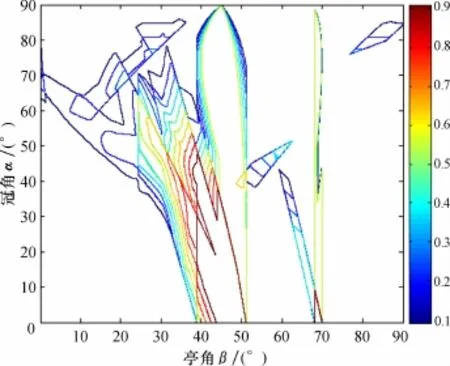
图5 冠部入射光线返回值(φ)等高线图Fig.5 Crown incident contour map of light return value(φ)
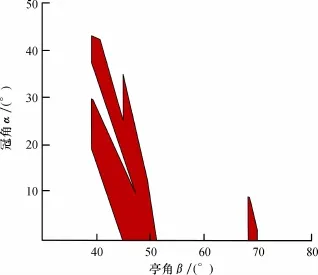
图6 冠部入射光线返回值(φ)1.0区域Fig.6 Area of 1.0 incident light return value from the crown
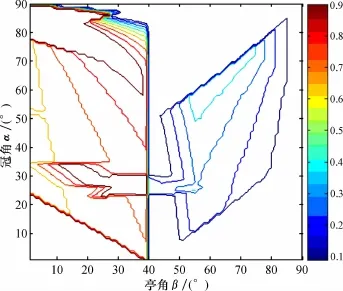
图7 亭部入射光线返回值(φ)等高线图Fig.7 Pavilion incident contour map of light return value(φ)
2.2均匀度分析
光线返回值达到1.0时,从理论上讲,钻石的明亮度应该达到最大程度,如果从冠部射出的光线分布不均匀,势必会存在不同明亮度的区域,将亮度暗淡的区域简称为暗淡区域。由于平行光线在二维平面反射时其间距不会改变,设进入钻石内部后的两条相邻光线之间的间距为d1,只要光线能射出钻石,两条光线之间的距离不会超过d1/cos i(i为钻石的临界角),提取成功射出冠部的所有光线与冠部交点的坐标,计算这些相邻点之间的距离,距离超过d1/cos i的范围即为暗淡区域,根据这些区域的具体坐标可知其在冠部的位置并计算出暗淡区域的面积与腰围面积的比值。光源从冠部照射时暗区比值(SD)等高线图见图8。
考虑到现代圆形明亮琢型的冠部和亭部主刻面角度的变化范围,本次研究对常见冠角和亭角的变化范围的角度以及不同台宽比的组合进行了计算和模拟。本文仅以台宽比为60%的圆形明亮琢型的钻石为例来进行说明。当亭角的大小介于37.1°~40.0°,冠角的范围为30.4°~44.4°时,光线在现代圆形明亮琢型冠部的分布是较均匀的,暗区比值小于0.1,且暗淡区域位于上腰刻面紧靠腰围的部分。前人的研究发现[7]:现代圆形明亮琢型的钻石腰围部分存在漏光现象。与本次用MATLAB模拟的暗淡区域的位置是一致的。根据模拟的结果,亭角越小光线越发散,且钻石的明亮度也得不到很好的体现。当亭部主刻面的角度在40.0°~41.0°变化时,尽管其暗区比值略大于0.1,但是暗区位于钻石的腰部边缘,呈圆环状,面积比率虽然稍大,但圆环的宽度变化却不明显,且出射光线斜率较大,即出射光线较集中,亭部主刻面的角度在此范围内的圆形明亮琢型也能提高钻石原石的利用率。因此,亭角在39.0°~41.0°范围内是比较理想的。此范围与IDC公布的理想圆形明亮琢型的亭角范围相一致,表明以光线返回值和暗区比值来推算钻石圆形明亮琢型的亭角大小具有较高的准确性与实用性。
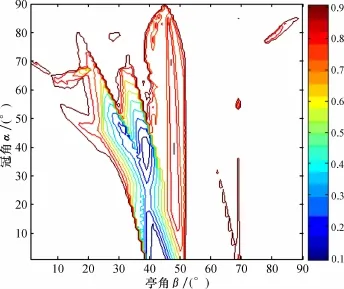
图 8 暗区比值(SD)等高线图Fig.8 Contour map of the dark area value(SD)
2.3色散角度及冠角的推导
宝石的色散值通常是采用弗朗霍芬谱线中的G线(波长为430.8 nm)和B线(波长为686.7 nm)所测得的折射率的差值来表示。对钻石而言,NG= 2.451,NB=2.407,则色散值D钻石=NG-NB= 0.044。当白光从钻石内部向空气折射时会发生色散(图9),只有当钻石的色散角θ较大时,钻石才表现出较强烈的火彩效应。根据光从光密介质进入光疏介质的折射率公式N=sin θ折射角/sin θ入射角,可得
θ折射角=arcsin(N·sin θ入射角),(6)色散角θ等于红光的折射角减去紫光的折射角,即
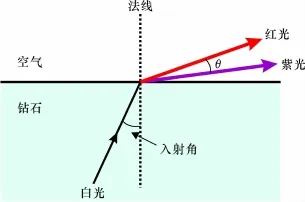
图9 白光从钻石向空气折射时发生色散Fig.9 White light dispersion of refraction from the diamond into the air

根据式(7),可以作出入射角与色散角之间的关系图(图10),当光线从钻石向空气折射时,入射角极限靠近临界角时色散角达到最大值
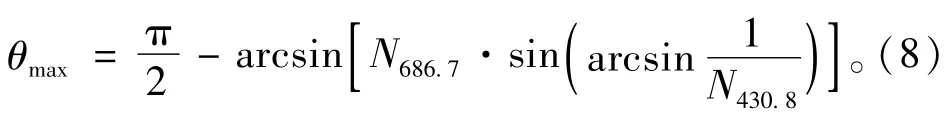
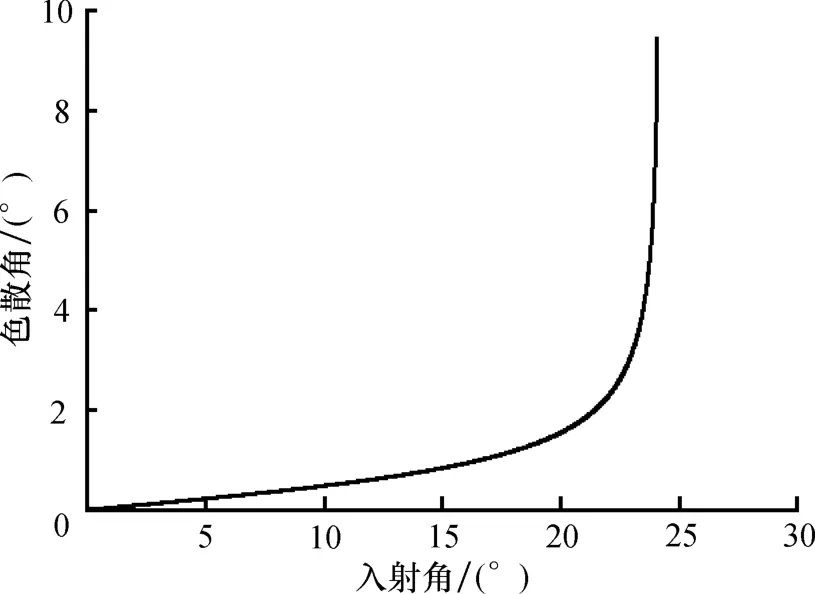
图10 色散角随入射角度变化的函数关系图Fig.10 Function diagram of the dispersion angle variation with incident angle
从上述分析可知:亭角的大小是影响现代圆形明亮琢型亮度的主要因素,而火彩的强弱与冠角及台宽比密切相关。色散角达到最大时,钻石的火彩效应最强烈。根据对钻石内部光线路径的模拟,光线在亭部经过两次全内反射到达冠部时,满足不等式(5)则光线能够顺利射出。当光线垂直台面入射,冠角α极限靠近π+i-4β时能够得到最大的色散角;当光线倾斜入射(光线与台面的夹角小于90°)时,光线在亭部全内反射后到达冠部的角度会增大;当α=π+i-4β时倾斜入射的光线将弹射回钻石内部,从而损失了火彩,因此α= π+i-4β的角度应为冠角的最大值。如图11所示,当入射光源逐渐向右侧倾斜时,其出射时与左侧冠部的交点也逐渐向台面移动,当交点到达冠部主刻面与台面的交点时,光线以最大的折射角射出。为了使从冠部入射的光线能够顺利从冠部折射出去,且色散角度最大,需让钻石内部的出射光线与冠部主刻面的夹角大小尽量接近临界角,此时光线在钻石内部的路径与台面法线成对称关系(图12),且不随台宽比大小及亭角变化而变化。由图12可知,当α+2β-π/2=i时,α为最小值,即αmin=π/2 +i-2β。
在亮度较高的切磨比例范围内,从台面入射的光主要从冠部主刻面、星刻面和上腰刻面射出,从台面射出的光主要是从冠部主刻面、星刻面和上腰刻面入射的光。光从冠部主刻面、星刻面和上腰刻面射出时的色散角远远大于从台面射出时的色散角(图13),因此冠部主刻面、星刻面和上腰刻面是观察现代圆形明亮琢型火彩的最佳区域,台面则是体现钻石亮度的最佳区域。同时,冠部射出的光线,其在钻石内部与冠部主刻面、星刻面或上腰刻面的角度越接近临界角,现代圆形明亮琢型钻石表现出的火彩越强烈。
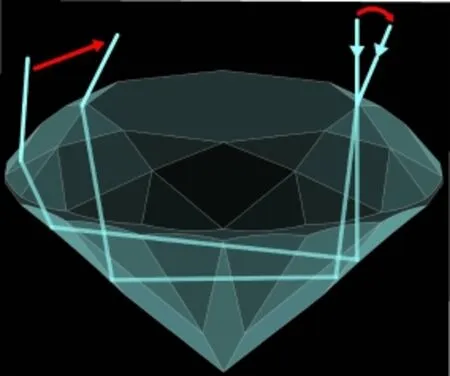
图11 光线出射点偏移Fig.11 Light emitting point offset
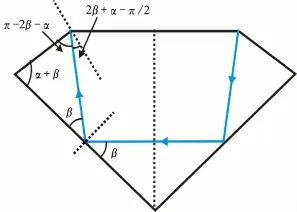
图12 最小冠角对应的光路图Fig.12 Light path of the minimum crown angle
实际情况中光源的照射方向是随机的,正确评价现代圆形明亮琢型钻石的火彩效果必须将所有的光源方向均考虑在内,因此,本次研究通过比较不同冠角对应的加权平均色散角来确定最优的冠角
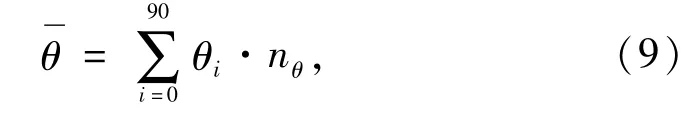
式中:i为光源与竖直方向的夹角;θi为色散角;nθ为产生色散角光线的数量百分比。通过计算发现,当亭角的大小一定时,存在唯一大小的冠角使加权平均色散角出现明显的峰值。图14是亭角为40.8°时,冠角与加权平均色散角的关系图,冠角为33.2°所对应的钻石加权平均色散角达到最大,即钻石出现最佳的火彩效果。通过计算和模拟,获得了一系列能够出现最佳火彩效果的亭角、冠角及台宽比的组合,表1列出了部分亭角、冠角及台宽比的组合。
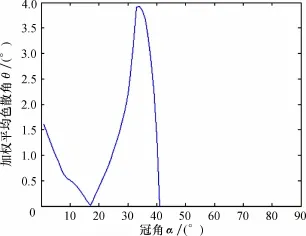
图14 冠角与加权平均色散角的关系(β=40.8°)Fig.14 Relationship between crown angle and weighted average dispersion angles
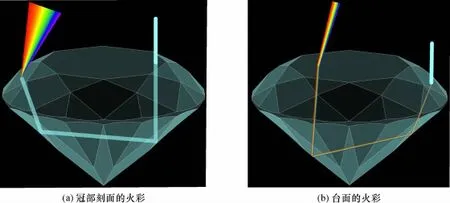
图13 钻石火彩形成的光路模拟图Fig.13 Simulating diagram of diamond fire
2.4台宽比的推导
根据MATLAB的模拟,台宽比只要超过某一比值就对光线返回值(φ)及暗区比值(SD)无影响,这一比值为最小台宽比(Amin)。当A<Amin时,一部分从冠部入射的光线会回到另一侧的冠部并且发生全内反射而无法射出,从而损失了亮度,也就是光线返回值能达到最大的前提条件是台宽比的取值范围在Amin~100%。在这个范围内,台宽比越小,加权平均色散角的权数也就越大,色散效果越好。不同的亭角与冠角对应着不同的最小台宽比(Amin),表1给出了部分亭角及冠角对应的最小台宽比(Amin)。
2.5几种圆形明亮琢型钻石的明亮度分析
在全球范围内,不同的国家和地区推出了各自加工和评价圆形明亮琢型钻石的标准,其中,最具代表性的琢型包括Tolkowsky、Eppler和Scan D N的钻石琢型比例。根据前文的分析,本次研究从光线返回值、暗区比值、亭角对应的最佳冠角及最小台宽比4方面对目前比较流行的4种钻石琢型的明亮度进行了模拟和计算,它们的台宽比、冠角和亭角的大小以及评价圆形明亮琢型明亮度的评价因子(光线返回值、暗区比值、亭角所对应的最佳冠角和各琢型所对应的最小台宽比)分别列于表2。对比发现,不同比例的圆形明亮琢型钻石的光线返回值几乎都接近1.00,但暗区比值的大小明显不同:Scan D N琢型的暗区比值只有0.221 7,而Tolkowsky琢型的暗区比值为0.293 6,在3种圆形明亮琢型钻石中是最大的。由于Tolkowsky琢型不仅台宽比偏小,而且没有从统计学的角度充分考虑使钻石达到最佳火彩的冠角,从而使冠角偏大,火彩和亮度都有不同程度的损失,因此,这种切工已逐步被淘汰。通过模拟发现Eppler琢型具有较为理想的亭角及冠角,但由于其台宽比偏小从而损失了部分的亮度,可以考虑适当增加一些台宽来使亮度达到最大化,以尽可能的体现出钻石固有的美观性。Scan D N琢型的比例与模型计算的理想化琢型也存在一定的偏差,与模型对比,Scan D N琢型的冠角偏大,不能最好的体现钻石的火彩,而且在腰围直径相同的情况下,无疑要增加钻石的用料。若适当减小冠角,不但能够更好地显示火彩,而且可以降低成本。虽然偏大的冠角能够适当的增加钻石成品的重量,但是在现代的钻石琢型的设计中,更好的明亮度效果已经比保重更能提升钻石的价值。一颗钻石的珍稀性永远不会改变,但品质性会被切工好坏所改变,也会极大影响钻石的长久价值[8]。随着钻石切磨技术的不断发展,使更加精准的切磨钻石工艺成为可能,为了追求极致的明亮度效果,需要设计出更为精确的钻石切磨比例。总之,通过模型的计算和分析,可以通过光线返回值、暗区比值及加权平均色散角等因素来评价不同比例和角度的圆形明亮琢型钻石的明亮度,为钻石琢型的改进提供了具体依据。
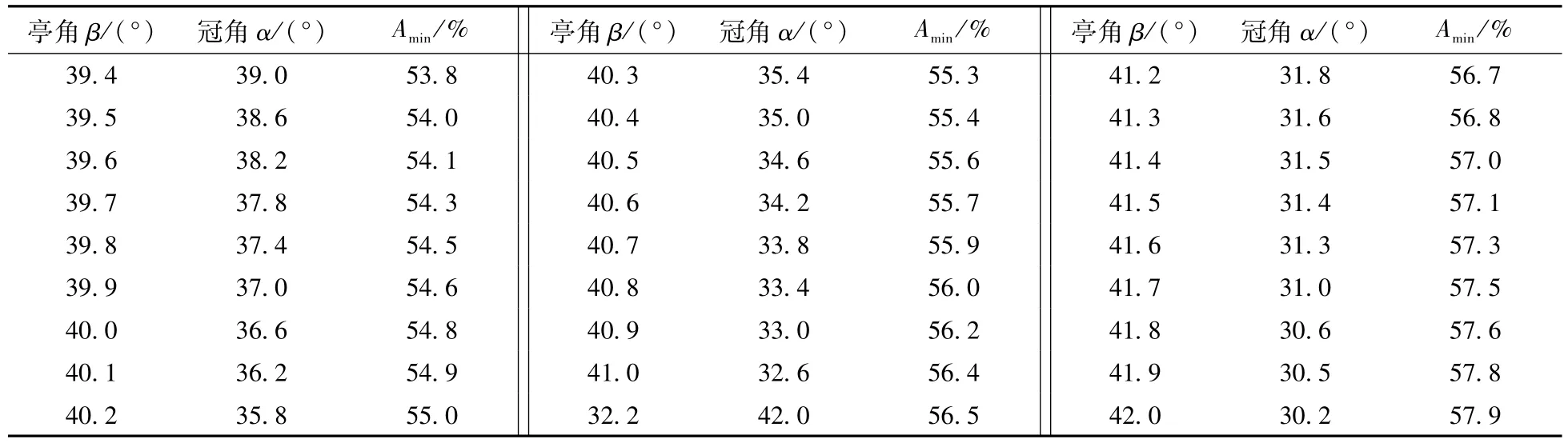
表1 部分具有最佳火彩的亭角与冠角的组合Table 1 Some matching groups with the best fire of the pavilion angles and crown angles

表2 几种不同比例圆形明亮琢型的明亮度评价Table 2 Intensity evaluations on several different cutting ratios of the round brilliant cut diamond
3 结 论
利用MATLAB强大的计算及绘图功能精准地模拟了现代圆形明亮琢型钻石内部的光线传播情况,从光线返回值、暗区比值和加权平均色散角等方面分析探讨了影响圆形明亮琢型钻石明亮度的各种因素,对目前流行的3种圆形明亮琢型的明亮度进行了对比分析,获得几点认识:
(1)圆形明亮琢型钻石的亮度主要来自冠部入射的光线,从亭部进入钻石的光线几乎不能从冠部射出,对钻石的亮度几乎没有贡献。亭角的大小决定了从冠部入射的光线能否返回冠部,但现代圆形明亮琢型切磨比例范围内的钻石腰部普遍存在漏光现象,模拟分析认为:亭角在39.0°~41.0°范围内较为合适,具有最大光线返回值及较小的暗区比值。
(2)钻石火彩的强弱与冠角的大小及台宽比密切相关。通过加权平均色散角计算和分析:当亭角的大小一定时,存在唯一大小的冠角使加权平均色散角出现明显的峰值,从而获得能够出现最佳火彩效果的亭角与冠角的组合。当钻石的台宽比大于最小台宽比Amin时,台宽比对亮度无影响,在Amin~100%范围内,台宽比越小,加权平均色散角的权数越大,火彩效果越好。
(3)以光线返回值、暗区比值及加权平均色散角能够较好的评价不同切磨比例圆形明亮琢型钻石的明亮度。
[1]英国宝石协会和宝石检测实验室.宝石学基础教程[M].陈钟惠,译.武汉:中国地质大学出版社,2004:313-332.
[2]周汉利.宝石琢型设计及加工工艺学[M].武汉:中国地质大学出版社,2009:23-34.
[3]Tolkowsky M.Diamond Design:A Study of the Reflection and Refraction of Light in a Diamond[M].London:E&F.N. Spon,1919.
[4]GB/T 16554—2010,钻石分级[S].
[5]Hemphill T S,Reinitz I M,Johnson M L,et al.Modeling the appearance of the round brilliant cut diamond:An analysis of brilliance[J].Gems&Gemology,1998,34(3):158-183.
[6]武文龙.钻石切工—— “4C”标准的唯一人为因素 [J].艺术市场,2013(27):61-65.
[7]Cowing M.Diamond brilliance:Theories,measurement and judgment[J].Journal of Gemology,2000,27(4):209-227.
[8]刘瑞梅.钻石切工营销的现实意义[J].中国黄金珠宝,2011(6):60-65.
Investigation on cutting ratio for round brilliant cut diamond
YU Xin-yuan1,RUAN Qing-feng1,YU Yuan-ming2,SONG Lin1,YANG Yang1,ZHANG Shi1
(1.College of Earth Sciences,Guilin University of Technology,Guilin 541004,China;2.School of Economics,Xiamen University,Xiamen 361005,China)
The optical path in diamond is simulated by the technique of MATLAB,and a series of parallel and equidistant lights are selected.The crown and pavilion of the diamond are illuminated respectively.This paper focuses on the influence of different cutting ratios on diamond intensity and fire,under vertical incident light changing to oblique incidence light.Various factors,such as light returning values,dark region values and weighted average dispersion angles,which have impact on the intensity and fire of round brilliant cut diamond,are analyzed and discussed,and the relationship of various factors to achieve the best processing effect is given. The simulation analysis shows that the pavilion angle is more suitable in the range of 39.0°to 41.0°,and has maximum light return and smaller dark area ratio.The calculation and analysis results of the weighted average dispersion angle shows that when the size of the pavilion angle is determined,only a crown angle makes the curve of weighted average dispersion angle appear obvious peak,and the combination of pavilion angle and crown angle which can appear the best fire color is also obtained.When table percentage of diamond is larger than the minimum table percentage(Amin),the table percentage has no effect on the brilliance.In the range of Aminto 100%,when the table percentage is smaller,the weight of weighted average dispersion angle is bigger,and the fire is better.
diamond;round brilliant cut;brilliance;fire;computer simulation
P619.28;TP391.75;TS933.3
A
1674-9057(2016)03-0435-09
10.3969/j.issn.1674-9057.2016.03.004
2015-01-23
国家自然科学基金项目(41362004)
俞鑫源 (1988—),女,硕士,研究方向:宝石矿物学,461157940@qq.com。
阮青锋,博士,副教授,rqfgut@163.com。
引文格式:俞鑫源,阮青锋,俞渊铭,等.圆形明亮琢型钻石切磨比例的探讨[J].桂林理工大学学报,2016,36(3):435-443.

