PRESENT代数故障攻击的改进与评估

黄静，赵新杰，张帆，郭世泽，周平，陈浩，杨建

（1. 61541部队3室，北京 100083；2. 北方电子设备研究所，北京 100191；3. 浙江大学信息与电子工程学院，浙江 杭州 310027；4. 保密通信重点实验室，四川 成都 610041；5. 军械工程学院信息工程系，河北 石家庄 050003）

PRESENT代数故障攻击的改进与评估

黄静1，赵新杰2，张帆3,4，郭世泽2，周平5，陈浩5，杨建3

（1. 61541部队3室，北京 100083；2. 北方电子设备研究所，北京 100191；3. 浙江大学信息与电子工程学院，浙江 杭州 310027；4. 保密通信重点实验室，四川 成都 610041；5. 军械工程学院信息工程系，河北 石家庄 050003）

提出了一种基于代数分析的PRESENT故障攻击改进方法，将代数分析用于密码和故障方程构建，通过逆向构建加密方程来加快求解速度；提出了一种故障注入后的密钥剩余熵评估方法，可评估不同故障模型下的PRESENT抗故障攻击安全性；最后对智能卡上的8位智能卡上的PRESENT实现进行了时钟毛刺故障注入，最好情况下1次故障注入即可恢复主密钥，这是PRESENT故障攻击在数据复杂度上的最好结果。

代数分析；轻量级分组密码；故障攻击；可满足性求解；时钟毛刺

1 引言

近年来，物联网的发展热潮带动了便携设备、无线传感器、智能卡等微型计算设备的广泛应用。不同于传统的计算设备，这些微型设备的计算能力有限、存储容量低、功耗要求低，传统的分组密码实现在这些设备上略显庞大，会增加物联网功耗、降低效率。因此，轻量级分组密码应运而生，典型算法包括：PRESENT、MIBS、LED、Piccolo、LBlock等，这些算法大都可在3 000个电路门内实现，特别适用于资源受限环境下的加解密需要。

PRESENT是Bogdanov等[1]提出的一种超轻量级分组密码算法。算法采用SPN结构，分组长度为64位，密钥长度支持 80位和 128位，分别对应PRESENT-80和PRESENT-128。由于PRESENT采用了基于位的置换操作，硬件执行效率很高，PRESENT-80加密仅需 1 570个门电路。目前，PRESENT-80已经被选定为80位的国际轻量级分组密码标准ISO/IEC 29192-2；基于PRESENT-80可以设计轻量级散列算法[2]。当前，PRESENT的安全性分析主要从设计安全性和实现安全性 2个层面进行。

在设计安全性分析方面，文献[3～5]基于差分攻击对PRESENT进行了分析，最多可以分析到26轮；文献[6,7]基于线性攻击对PRESENT进行了分析，最多可以分析到27轮；Albrecht等[8]基于代数攻击对PRESENT进行了分析，最多可以分析到19轮；在2015年的美密会上，Blondeau[9]构建了一个已知密钥的区分器，可以对全轮的PRESENT进行分析，攻击的数据复杂度为235.58，时间复杂度为256次加密。可以看出，全轮的PRESENT仍然相对安全，传统密码分析方法在有限复杂度内攻破 PRESENT的可行性不高。

在实现安全性方面，现有研究主要集中在旁路攻击和故障攻击2个方面。在旁路攻击方面，文献[10,11]对PRESENT抗差分功耗分析、相关功耗分析能力进行了评估，几百条功耗曲线可以恢复完整密钥；文献[12]将代数分析引入到PRESENT功耗攻击，一条加密曲线可以恢复完整密钥，但需要在已知密钥下预先采集几百条曲线建立功耗模板；文献[13]将立方体分析引入到PRESENT功耗攻击中，990条功耗曲线可在未知算法设计下恢复PRESENT-80的72位密钥。在故障攻击方面，Li等[14]首次提出了针对PRESENT-80的差分故障攻击，基于Nibble（半字节）故障模型，在故障注入到第 29轮的查找S盒输入时，40～50次故障注入可以恢复64位后白化密钥；Wang等[15]提出了针对 PRESENT密钥扩展的差分故障攻击，假定1个Nibble的故障能够注入到第31轮密钥生成中，64次故障注入可以恢复51位密钥；Zhao等[16]提出了一种基于故障传播模式分析的PRESENT差分故障攻击，基于第29轮Nibble故障模型，可使用8次和16次故障注入分别将PRESENT-80/128的主密钥搜索空间降低到214.7和221.1；Gu等[17]将统计分析引入到故障分析，基于Nibble故障模型，通过构建最大似然和欧几里德距离区分器，可使用10 000次故障注入对倒数 8轮以内的故障进行分析；Wu等[18]将代数攻击引入到PRESENT故障分析，通过分析差分S盒，可基于第29轮Nibble故障模型使用 2次有效错误密文恢复主密钥；Jeong等[19]基于第28轮双字节故障模型，可使用2次和3次故障注入将PRESENT-80/128的密钥搜索空间降低到1.7和222.3。

通过分析已有PRESENT故障攻击，本文发现已有攻击大都基于Nibble故障模型，最多可以分析倒数3轮。已有的差分故障攻击需要手工对故障传播路径进行分析，恢复密钥所需故障注入次数相对较多[14～16]，文献[19]所需的故障次数虽然较少，但双字节故障在实际环境中（PRESENT大都是用于8位处理器）很难注入；同时，已有PRESENT统计故障攻击需要对大量错误密文进行统计分析，在故障利用率上并不是最优的；已有的PRESENT代数故障分析[18]需要特定的故障密文，为了得到这些特定的故障密文，攻击者需要进行多次故障注入和筛选，对故障模型有着特殊的要求，在故障注入次数上也不是最优的。

为分析、改进、评估已有PRESENT故障攻击，本文开展了大量的研究工作，主要创新点如下。

1)本文提出了一种基于代数分析的PRESENT故障攻击改进方法，通过逆向构建加密方程来加快求解速度，构建了更为紧凑、适合代数故障分析的方程，可适用到不同故障模型，并利用解析器进行密钥自动化求解。

2)本文提出了一种故障注入后的密钥剩余熵评估方法，通过仿真实验评估了不同故障模型下的PRESENT抗故障攻击安全性。实验结果可对已有PRESENT故障攻击进行解释和分析，得到更准确的故障注入后的密钥搜索空间降低情况；同时可改进已有攻击，寻找最优故障模型，降低攻击所需故障注入次数、延伸故障分析轮数。

3)基于 8位故障模型，首次对符合 ISO/IEC 7816-3协议智能卡上的PRESENT软件实现进行了2类故障注入物理实验，最佳结果表明1次故障注入可恢复PRESENT密钥，这是PRESENT故障攻击在数据复杂度方面的最好结果。

需要说明的是，本文方法可用于指导攻击者根据故障注入条件选取最佳故障模型、新型算法设计者评估设计算法抗故障攻击能力、已有算法实现者对一定轮数内的算法进行故障攻击防护。

2 PRESENT算法与故障模型

2.1 PRESENT算法设计

PRESENT采用SPN结构，分组长度为64位，支持80位、128位2种密钥长度，共迭代31轮。

1)加密过程

轮函数F由轮密钥加、S盒代换、移位置换这3部分组成。

① 轮密钥加：64位轮输入同轮密钥异或。

② S盒代换：轮密钥加输出查找16次4进4出的S盒。

③ 移位置换：通过置换表P(i)对S盒代换输出按位重新排列。

为提高算法安全性，PRESENT在第31轮后使用64位白化密钥K32进行后期白化操作。

2)密钥扩展算法

将初始主密钥存储在寄存器 K中，表示为k0k1…k79。第 i轮密钥Ki由寄存器K的前64位组成。当生成第i轮密钥Ki后，K通过以下方法进行更新。

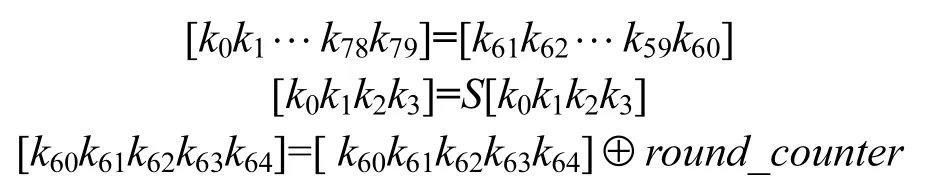
其中，round_counter为当前的加密轮数。

2.2 PRESENT算法软件实现

PRESENT算法的典型软件实现包括2种[20]：1)开销优先实现 PRESENT_SIZE，使用了 4进 4出的S盒，其中，轮密钥加、S盒代换以Nibble为基本运算单位，优点是实现规模小，代码更加紧凑，但不足是速度较慢；2)速度优先实现 PRESENT_SPEED，将2个相邻的S盒使用1个8进8出的查找表来实现，这样轮密钥加、S盒代换均以字节为单位进行计算，执行速度较快。

2.3 故障模型

一般来说，故障模型由5元组F(X,λ,w,t,f)构成。

X：故障注入针对的中间状态。

X*：故障注入后错误的中间状态。

λ：X的长度。

w：故障宽度。

Xi：X中第i个单元，X=X1|| X2||…||Xm。

t：故障单元索引。

f：故障差分，f=Xt+Xt*。

本文利用的故障模型为PRESENT加密过程中查找S盒操作产生故障，具体的故障模型参数设置见后续几个小节。

3 改进的PRESENT代数故障分析方法

3.1 攻击框架

图1给出了本文利用的代数故障攻击框架，由以下3部分组成。

1)故障注入

图1 代数故障攻击框架

故障注入是指攻击者通过光学辐射、电压毛刺、时钟毛刺等方法修改芯片工作条件，使密码算法在某个轮次计算过程中注入故障产生错误，并将错误传播至密文。故障注入属于在线攻击阶段。故障注入方法和目标密码芯片的类型与故障模型直接相关。如对于8位微控制器上的软件实现，使用电压或者时钟故障诱导的故障一般为8位，而使用光学辐射诱导则可以达到单位精度。

2)方程构建

方程构建是指攻击者构建出给定正确和错误加密样本的代数方程，属于离线攻击阶段。一般来说，攻击者需要构建出密码算法和故障方程。在密码算法代数方程构建方面，攻击者可以采取不同的策略。一方面，可以构建出从故障注入轮到密文正确和错误加密的代数方程，然后加上一个正确加密的全轮方程（称为校验方程），并和故障方程联立求解恢复唯一的密钥；同时，攻击者也可以不使用校验方程，此时方程可能会有多个可满足解，可以利用支持多个解的解析器来统计故障注入后的密钥搜索空间。另一方面，攻击者可以选取不同方法构建密码或者故障方程，如S盒的方程构建就有待定系数法、矩阵法、真值表构造法等。此外，攻击者还可以选定是正向还是逆向构建密码算法方程。

3)方程求解

首先将代数方程转化为解析器可以理解的格式，然后利用解析器进行密钥求解。方程求解策略有多种，如基于可满足性问题的求解策略，典型解析器包括zChaff、MiniSAT、CryptoMiniSAT等，再如基于混合整数编程问题的求解策略，典型解析器有 SCIP、Gurobi等。本文选取专门用于密码代数分析的解析器CryptoMiniSAT进行方程求解，可以自动对任意长度的异或表达式进行切割，十分便于密码方程构建。此外，CryptoMiniSAT支持多个解的输出，可以统计故障注入后的密钥搜索空间。

3.2 PRESENT代数方程构建

1)代数故障分析密码整体结构构建策略

在代数故障分析中，密钥分析常是从密文开始，因此从密文开始反向构建加密方程，可以有效降低求解时间[21,22]，构建方法如图2所示。同时，密钥扩展方程建议也反向构建。PRESENT采用了SPN结构，每轮输出同输入有很大差异，需要首先求出每个密码操作逆运算函数，再为之建立方程。

图2 代数故障分析密码整体结构构建策略

2)PRESENT代数故障分析方程组构建算法算法1给出了PRESENT故障分析代数方程组构建过程，如下所示。

算法 1PRESENT代数故障分析方程组构建算法

输入故障注入数量(N)；注入故障的加密轮(r)；故障宽度(w)；故障位置是否已知标志位(b)

输出代数故障分析所需方程

Step1构建密钥扩展方程

If (b=1){//逆向构建全轮密钥扩展方程

For(i=31;i≥1;i− −)

GenerateKS_R(i);}

Else { //逆向构建倒数31−r轮密钥扩展方程

For(i=31;i≥r;i− −)

GenerateKS_R(i); }

Step2逆向构建倒数31−r轮正确和错误加密方程、故障方程

RandomPlaintextGenerating();//产生攻击所需的随机加密明文

For(i=0; ilt;N; i++){

Ci=E(Pi,K)//第i个明文正确加密

For(j=31; j≥r; j− −)//逆向构建倒数31−r轮加密方程

GenerateES_R(j);

Generate_Input_ES(Ci)//输入正确密文

Ci*=FaultInjecting(E(Pi,K))//第i个明文加密注入故障

For(j=31; j≥r; j− −)//逆向构建倒数31−r轮加密方程

GenerateES_R(j);

Generate_Input_ES(Ci*)//输入错误密文

Generate_Faults_ES(f=X+X*)//构建故障方程

Step3逆向构建验证故障方程

VerifyPlaintextGenerating(Pv)//生成随机验证明文

Cv=E(Pv,K)//验证明文正确加密

For(i=31; i≥1; i−−)//逆向构建全轮加密方程

GenerateES_R(i);

Generate_Input_ES(Pv,Cv)

可以看出，方程分为3部分。第1部分为密钥扩展方程，整个攻击过程中只需构建一次；第2部分为加密和故障方程，需要为每次正确和错误加密建立方程；第3部分为可选部分，主要构建用于密钥校验的明密文方程。需要说明的是，代数故障方程构建分为2种模式。第1种模式是含校验方程时，称为Type A模式，此时方程求解只有唯一解。第2种模式为不含校验方程模式，称之为Type B模式，此时代数方程会包含多个可满足解、代数方程规模较小，求解速度较快。

3)PRESENT密钥扩展方程构建

下面给出密钥扩展方程的逆向构建方法。正向密钥扩展函数由左移61位、查找S盒、异或轮常量组成，则逆向密钥扩展函数由异或轮常量、查找逆S盒、右移61位组成。

① 异或轮常量函数

令异或轮常量函数输入为(x0||x1||…||x79)，输出为(y0||y1||…||y79)，轮常量用(z0||z1||…||z79)来表示，则异或轮常量函数可表示为

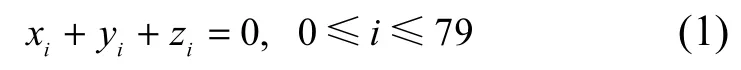
② 逆S盒函数

令逆 S盒函数输入为(x0||x1||x2||x3)，输出为(y0||y1||y2||y3)，则逆S盒代数方程可表示为

需要说明的是，PRESENT密钥扩展每轮只查找1次S盒。

③ 右移61位函数

令函数输入为(x0||x1||…||x79)，输出为(y0||y1||…||y79)，则右移函数代数方程可表示为

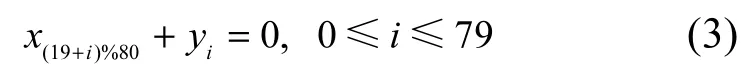
4)PRESENT加密方程构建

PRESENT加密轮函数由轮密钥加、S盒代换、置换函数组成，则逆轮函数由逆置换函数、逆S盒代换、逆轮密钥加组成。

① 逆置换函数

令逆置换函数输入为(x0||x1||…||x63)，输出为(y0||y1||…||y63)，则逆置换函数代数方程可表示为

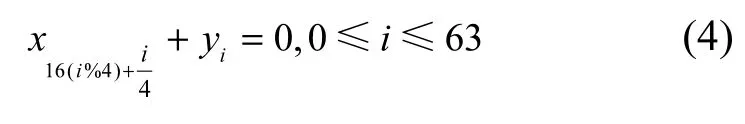
③ 逆S盒代换

逆S盒代换方程如式(2)所示。这里，每次需要查找16次S盒。

③ 逆轮密钥加

令逆S盒代换的输出为(x0||x1||…||x63)，轮密钥为(y0||y1||…||y63)，逆轮密钥加输出为(z0||z1||…||z63)，则逆轮密钥加可表示为

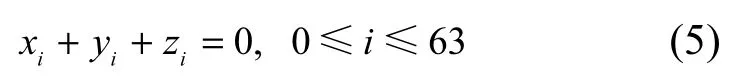
3.3 故障代数方程构建

令 X表示 λ位正确加密状态，则 X=(x0||x1||…||x63)；令X*表示注入宽度为w位的故障后的λ位错误加密状态，X*=(x0*||x1* ||…||x63*)，故障可能位置有m个令Z表示X和X*的故障差分。

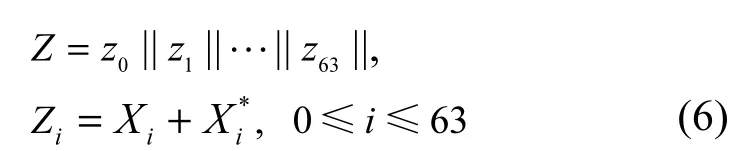
根据故障宽度大小w不同，Z可以被划分为m个w位变量，Z=(Z0||Z1||…||Zm−1)

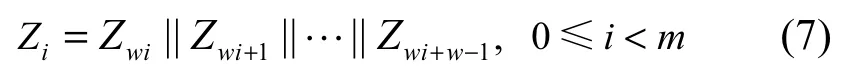
根据攻击者是否已知故障索引值t，Z可以用不同的代数方程来表示。

1)故障索引t已知

假设t值已知，则Z可表示为

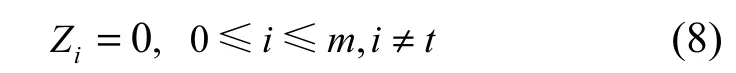
Zt是一个非0的w位变量，可通过引入单位变量ut来表示Zt是否非0。

根据式(8)和式(9)，Z可通过引入w+1个变量和w(m+1)+2个交集普通方程（CNF）变量来表示。

2)故障索引t未知

在实际攻击中，故障索引t可能是未知的，可通过引入m个变量ui来表示Zi是否被注入故障。

如果ui=0，则 Zi即为注入故障的位。由于 u0,u1,…,um−1有且只有一个为0，则可表示为

根据上式，Z可通过引入 m(w+2)个变量和m(2w+0.5m+1.5)+1个CNF变量来表示。需要说明的是，式(11)可适用于不同的w、m、λ参数。

3.4 主密钥搜索空间评估

由3.1节和3.2节可知，根据是否引入校验方程，代数故障分析方程求解可分为唯一解求解（Type A）和多个解求解（Type B）2种模式。需要说明的是，一般的可满足性问题（SAT）解析器大都仅支持 Type A模式，不支持 Type B模式，CryptoMiniSAT解析器从v2.9.4版本开始支持多个解输出。在Type B模式下，令φ(K)表示故障注入后的剩余密钥熵，即密钥搜索空间求 Log2结果，下面简要给出如何利用CryptoMiniSAT估计φ(K)。令L表示主密钥K的长度，N表示一次故障攻击的故障注入次数，θ表示输入的已知密钥位数量。为了准确地评估φ(K)，θ一般从最大值L开始设定，逐渐降低到0。令 η(θ)表示解析器，根据给定 θ得到的可满足解数量。在实际攻击中发现，如果一次代数故障攻击中可满足解的数量大于218，解析器很难在有限时间内找到所有解。为此，设定了一个多个解空间上限 τ。下面给出主密钥搜索空间的穷举算法。

算法2剩余密钥熵评估算法（Type B模式）

输入L,N,θ,τ

输出φ(K)

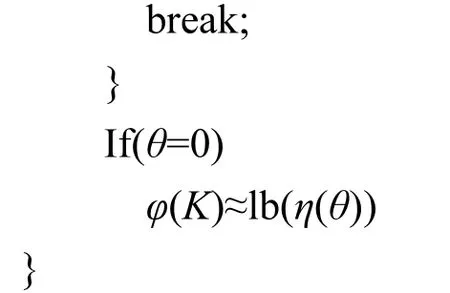
对于PRESENT攻击，L设定为80，τ设定为218。当 η(θ)≥τ 且 θ＞0 时，φ(K)≈θ+lb(η(θ))，由于已知的θ位密钥可能在后续攻击中被恢复，此时一般实际的 φ(K)值会比 θ+lb(η(θ))要小，也就是此时得到了φ(K)值的一个上限估计；当θ=0时，等价于在未知密钥下的代数故障攻击，φ(K)=lb(η(θ))。

4 PRESENT抗故障攻击能力评估

本节的故障注入是通过仿真实现的，故障攻击物理实验细节可参考第5节。

4.1 第29轮随机Nibble故障攻击

在N=1时，使用在第29轮S盒输入进行了注入随机Nibble（w=4）故障实验，攻击在Type B求解模式下执行了100次，得到的φ(K)统计如图3所示。

图3 第29轮注入单次Nibble故障后φ(K)统计

根据图3，φ(K)可被降低到54～78位，平均值为 70.58位，φ(K)平均被降低了 9.42位，8～10次故障注入即有望将 φ(K)降低到较小值。需要说明的是，φ(K)的波动主要取决于故障注入后在后续轮次中传播影响到的S盒数量。如果最后一轮查找S盒出错数量较少时，如2～4时，φ(K)的取值则较大；否则较小。

图4给出了第29轮注入8次随机Nibble故障后的密钥剩余熵 φ(K)的统计。可以看出，8次故障注入后φ(K)平均可被降低为8.13位。需要说明的是，8次故障注入是平均值，在故障影响的S盒数量较大的情况下，3次故障注入可将 φ(K)降低到较小范围。

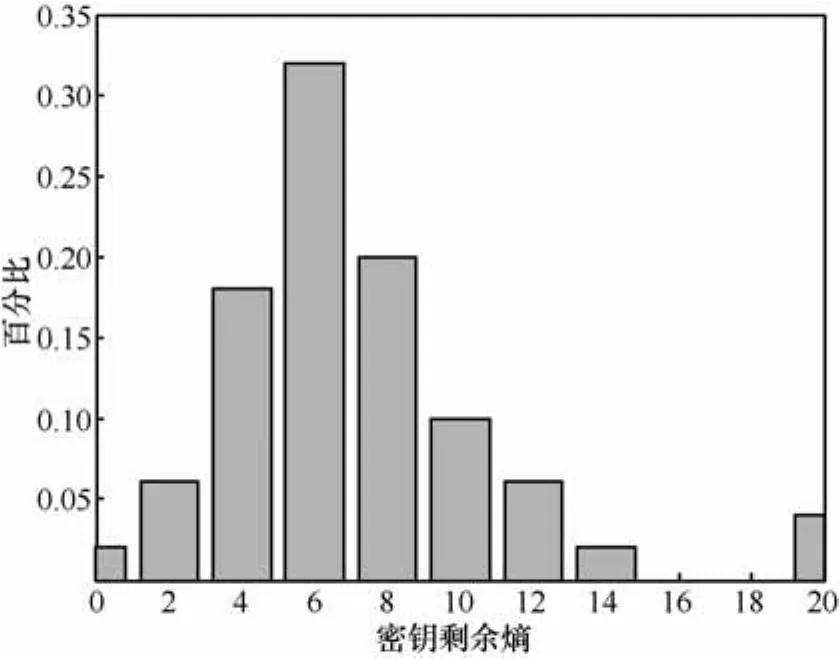
图4 第29轮注入8次Nibble故障后φ(K)统计

4.2 第28轮随机Nibble故障攻击

1)第28轮注入Nibble故障

在N=1时，在第28轮S盒输入进行了注入随机Nibble（w=4）故障实验，攻击执行了100次，得到的φ(K)统计如图5所示。

图5 第28轮注入1次Nibble故障后φ(K)统计

可以看出：φ(K)取值符合指数分布，取值范围大致为26～72，平均被降低到51.49，攻击效果比第29轮攻击好，2～3次故障注入有望恢复主密钥。

N=3时，100次故障攻击后φ(K)统计如图6所示。φ(K)可被降低到12以内，平均被降低到4.05。

4.3 不同故障宽度、深度攻击比较

为研究不同故障宽度对攻击的影响，首先对第29轮随机单位故障（w=1）、随机Nibble故障（w=4）、随机单字节故障（w=8）、随机双字节故障（w=16）、随机4字节故障（w=32）进行了代数故障攻击实验，分别执行100次攻击实验，得到的φ(K)统计如图7所示。

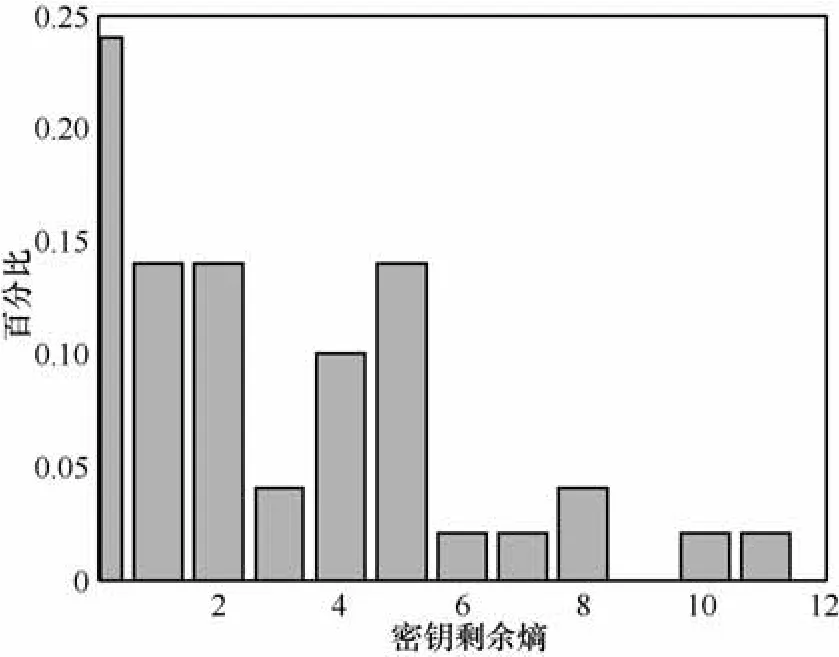
图6 第28轮注入3次Nibble故障后φ(K)统计

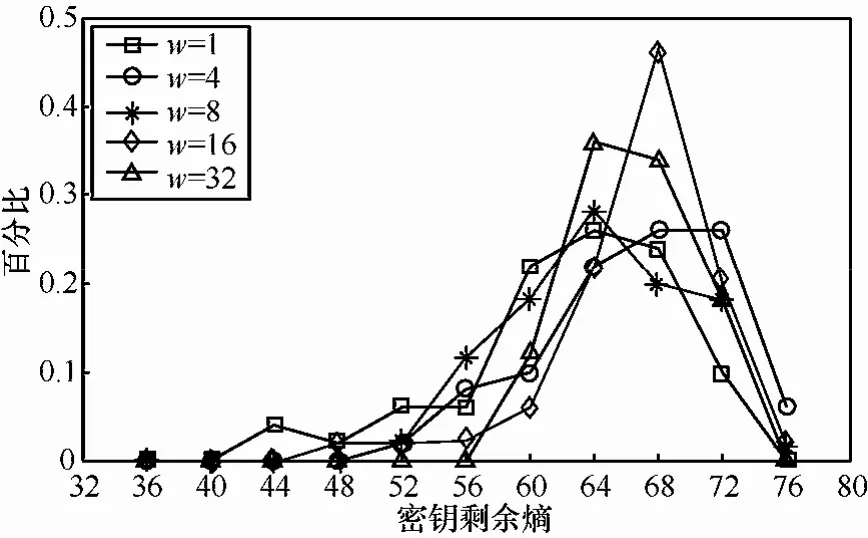
图7 第29轮注入不同宽度故障φ(K)统计

可以看出，φ(K)大致为44～76，如果故障传播影响的S盒较多，3次注入即可恢复80位主密钥。需要说明的是，Nibble随机故障模型下，如果攻击执行次数较多（一般要 10万次左右），从中筛选出第29轮1次故障注入后影响最后一轮16次查找S盒操作的故障样本，本文发现单次故障注入后可将 φ(K)降低到40以内，2次故障注入可恢复完整主密钥。

表1给出了一次故障注入下PRESENT代数故障攻击平均可恢复的密钥位（即 80−φ(K)）。第 29轮注入故障时，单位故障模型平均恢复密钥位最多；单字节故障模型次之，Nibble、双字节故障模型相对接近；4字节故障模型则接近于单字节故障模型，这主要是由于4字节故障模型在很大概率上可以导致最后一轮16次查找S盒出错导致的。

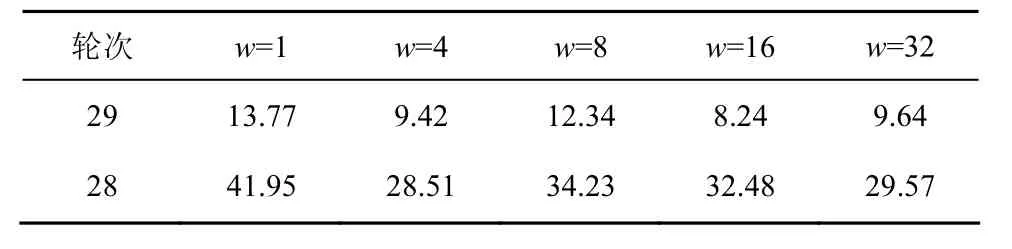
表1 N=1时攻击平均恢复密钥位

为了解不同深度、宽度条件下的攻击影响，本文将攻击扩展到第28轮，针对w的5个参数值分别进行了100次攻击实验，得到的φ(K)统计如图8所示。1次故障注入下w=1、4、8、16时均有很大概率将φ(K)降低到40以内，有的甚至可降低到20以内，1～2次故障注入后有望恢复主密钥；w=32时大部分情况下可将φ(K)降低到48～60，大约3次故障注入后有望恢复主密钥。

第 28轮一次故障注入下不同宽度平均可恢复的密钥位的统计见表1第2行，可以看出第28轮攻击恢复密钥位要多于第 29轮；单位故障攻击效果最好，其次为单字节、双字节故障模型，最后是Nibble和4字节故障模型。

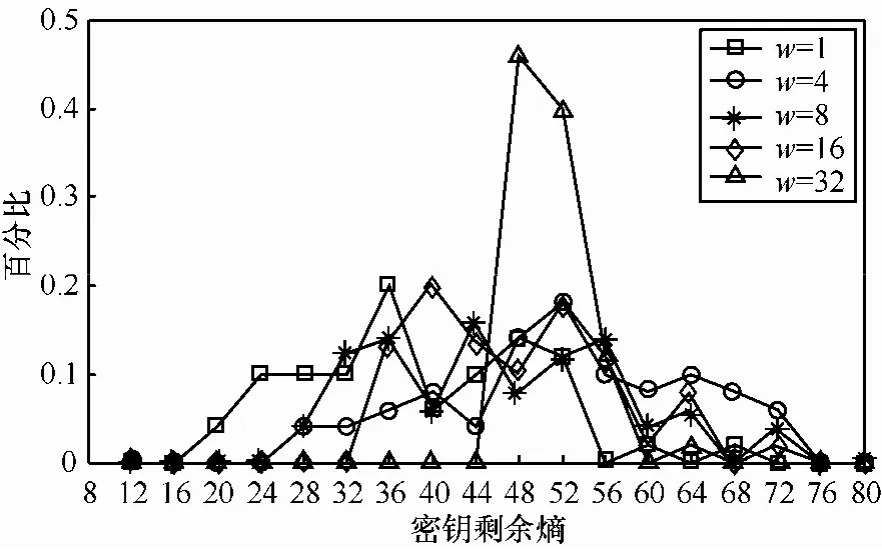
图8 第28轮注入不同宽度故障φ(K)统计

此外，本文还将攻击扩展至第 27轮，此时随着已知密钥位数量θ的减小，解析器求解速度越来越慢。实验大致可估计出当 θ=40时，可满足解数量大部分情况下仍为 1，这就意味着一次故障注入后至少恢复40位密钥，2次故障注入有望恢复主密钥。但实际攻击中，随着轮数的增加，解析器求解代数方程的复杂度较大，导致求解时间较长，2次故障注入本文在 24 h内也无法实现密钥恢复。为此，本文增大了故障注入样本量，5次故障注入可在1 h内恢复主密钥。

4.4 故障分析结果比较与解读

表2给出了本文与已有故障分析结果的比较。

1)第29轮故障攻击比较与解读

在第29轮注入故障，目前有4项研究工作，均基于Nibble故障模型。① Li等[14]的差分故障分析工作，在故障注入到第29轮的查找S盒输入时，40～50次故障注入可以恢复64位后白化密钥。② Zhao等[16]的基于故障传播模式分析的差分故障攻击工作，基于文献[14]相同故障模型，通过分析故障密文索引和差分特征来识别故障传播路径，8次故障注入分别将PRESENT-80/128的密钥搜索空间降低到214.7。③ Gu等[17]的统计故障分析，通过构建基于最大似然区分器和欧几里德距离区分器，10 000次故障注入可恢复最后一轮的64位后白化密钥。④ 吴等[18]的代数故障分析，通过筛选特定的故障密文，2次故障注入样本可恢复64位后白化密钥。

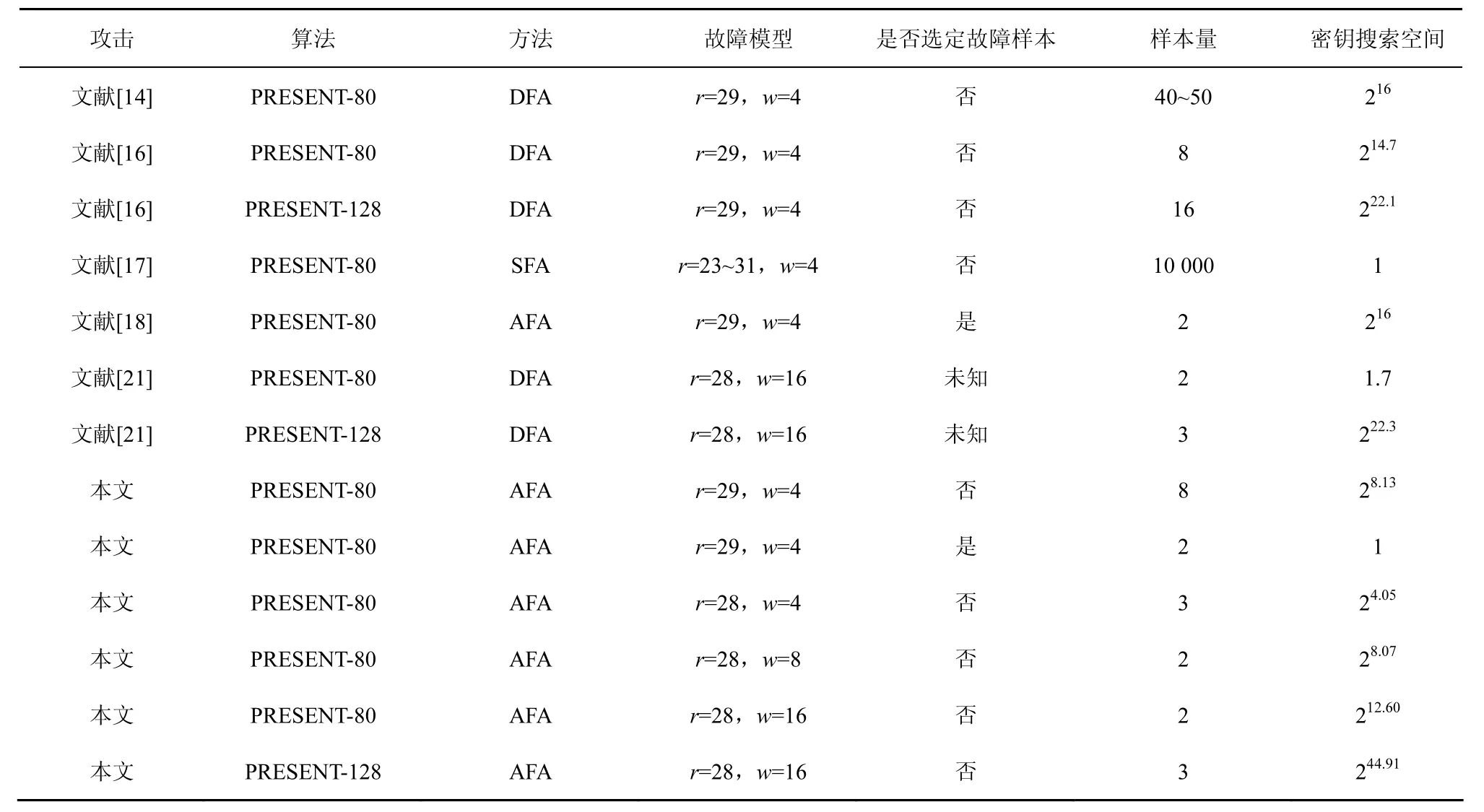
表2 PRESENT故障分析结果比较

已有工作受制于密码分析者对故障信息的利用率和密码分析认知能力，代数故障分析则将该问题转化为机器解析器求解问题，结果更加可靠。本文前面结果表明，第29轮注入单个随机Nibble故障平均可恢复9.42个位（如表1所示），8次故障注入后平均可将φ(K)降低到8.13，结果要优于文献[14]、文献[16]，这主要是由于解析器自动求解可充分分析故障注入位置至密文的所有故障信息导致的；同时，Gu等的统计故障分析依赖于构建的最大似然区分器和欧几里德距离区分器，在数据复杂度上并不是最优的，这一点在文献[17]中也明确提出了；吴等[18]的代数故障分析依赖于特定的故障模型，攻击者需要筛选出第29轮注入Nibble故障后密文的16个Nibble全出错的特定样本，2次故障注入可恢复 64位后白化密钥，而基于相同故障模型，利用本文方法可直接恢复 80位主密钥，结果要优于文献[18]。

2)第28轮故障攻击比较与解读

第28轮故障攻击有2项工作：① 文献[17]基于Nibble故障模型的统计故障分析，10 000次故障注入可恢复最后一轮的64位后白化密钥；② 文献[21]基于双字节故障模型的差分故障分析，可使用2次和3次故障注入分析将PRESENT-80/128的密钥搜索空间降低到1.7和222.3。

本文代数故障分析结果表明，文献[17]在第28轮Nibble故障攻击的数据复杂度仍不是最优的，3次故障注入即可将主密钥剩余熵平均降低到4.05；基于第28轮随机双字节故障模型，2次故障注入时执行了 100次攻击实验得到的 φ(K)统计如图 9所示，φ(K)的取值范围大致为0～40，平均值为12.60。由于文献[21]中仅给出使用 2次故障注入可将PRESENT-80密钥搜索空间降低到1.7，并没有给出攻击的重复执行次数和φ(K)的统计分布特征，其攻击结果可信度有待考证。文献[19]中攻击对故障注入可能有特定要求，要求每次故障注入都会产生最多的活跃S盒，从而使密钥恢复效率较高导致的，本文的攻击实验中主密钥剩余熵也可被降低到零也可说明该特性。

本文4.3节第28轮注入不同宽度故障攻击结果表明，第 28轮双字节故障模型并不是最优模型，单位故障模型和字节故障模型的攻击效果要优于双字节故障模型，如图9所示。

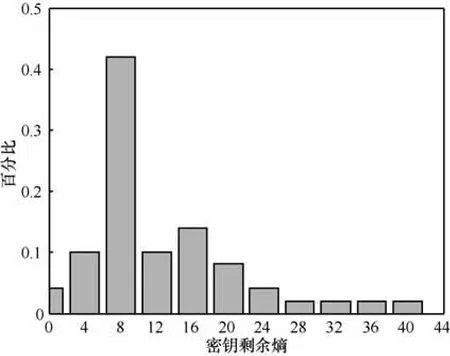
图9 第28轮注入2次随机双字节故障φ(K)统计

此外，基于双字节故障模型对PRESENT-128进行了攻击，N=3时，100次攻击后 φ(K)的统计分布特征如图10所示，128位主密钥熵可平均被降低到44.91，结果要大于文献[19]的222.3，本文猜测可能仍是文献[19]中攻击每次故障注入都会产生最多的活跃S盒，从而使密钥恢复效率较高导致的。

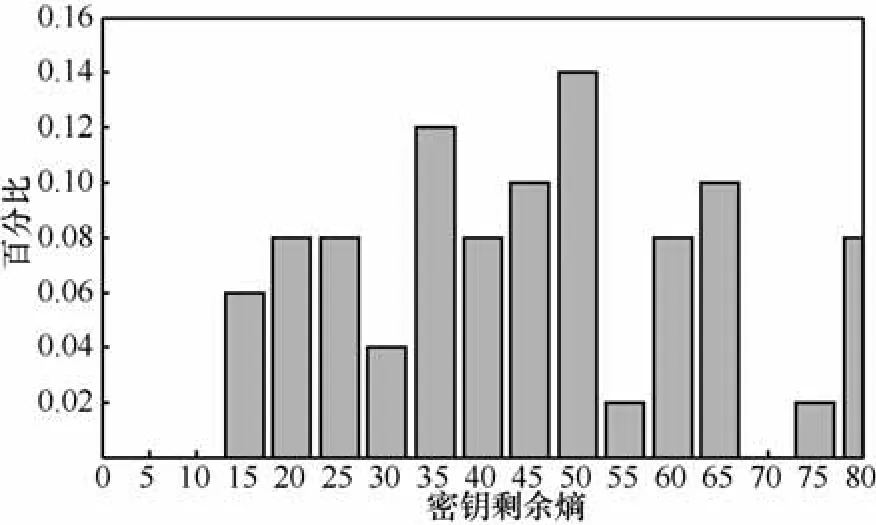
图10 第28轮注入3次随机双字节故障φ(K)统计

5 故障攻击物理实验

本节旨在对PRESENT在智能卡上的软件实现开展故障注入物理实验，研究不同条件下的故障注入成功率，以及现实中的故障模型，并验证本文故障分析结果的正确性。

需要说明的是，故障注入的方法有很多种，如电压毛刺、时钟毛刺、电磁辐射、激光照射等。其中，激光故障注入精度最高，可以到单比特，但需对芯片进行剖片，成本较高；电压和时钟毛刺注入故障成本较低，基本能够注入半字节或者单字节故障。因此，本文选取时钟毛刺作为故障注入手段。

5.1 实验配置

实验中，PRESENT实现在符合ISO/IEC 7816-3协议的智能卡上，核心为 ATMega163微控制器，工作频率为3.57 MHz，算法采用速度优先的8位软件实现。故障注入使用ChipWhisperer设备来实现，其中，时钟毛刺通过Xilinx Spartan 6 FPGA芯片来生成和控制。故障分析电脑配置为 Intel(R)Core(TM)I7-2640 CPU 2.80 GHz，4 GB内存，Win7 64位操作系统，解析器版本为CryptoMiniSAT v2.9.6。

5.2 基于时钟毛刺的故障注入

1)时钟毛刺生成过程

时钟毛刺是时钟信号中不规则的情形，使用时钟毛刺可以比较精确地向某一计算过程引入故障，例如对加密过程中的一个 8 位寄存器中的数据产生随机故障的效果，这也是许多故障攻击假设中所使用到的模型。图11是一个局部寄存器结构，CLK表示寄存器的时钟信号，r_in和r_out分别表示寄存器的输入和输出数据。Data input和Data output则是该电路的输入输出，在密码算法执行中常代表加密中间变量。

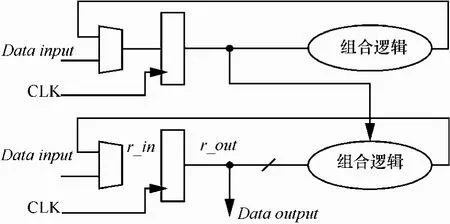
图11 局部寄存器电路

在每个时钟上升沿，寄存器进行数据读入和输出，且在每个时钟周期内，由于模拟电路设计和路径延时等原因，寄存器存在一段数据不稳定的时间。当2个相邻上升沿时间间隔大于该不稳定区间，寄存器输出数据和输入数据相等，电路运行正常；否则r_out值尚未稳定下来就输出到下一级电路，寄存器处于不稳定区间，r_out输出将是随机值，导致该部分电路运算出错。

实验中，使用Xilinx Spartan 6系列FPGA芯片来实现时钟毛刺的生成与精确控制，生成的时钟信号将作为密码芯片的时钟信号输入，如图12所示。输入时钟信号input_clk经2次相移后生成2路同频不同相的时钟信号，利用这2路信号，经过运算可以得到一串连续的脉冲信号毛刺。将该脉冲信号流与原始输入时钟信号 input_clk进行异或即可得到毛刺时钟信号 g_clk。上述 2次相移操作均是通过FPGA芯片中的数字时钟管理模块实现。

为精确控制故障注入位置，在指定时机产生毛刺，攻击者需要在input_clk和g_clk之间按需进行切换。切换是通过调节外部输入信号trigger的位置进行控制的，当FPGA检测到trigger信号拉高时，密码芯片的时钟输入切换为毛刺时钟，而当trigger信号为低电平时，密码芯片时钟输入恢复为正常时钟。

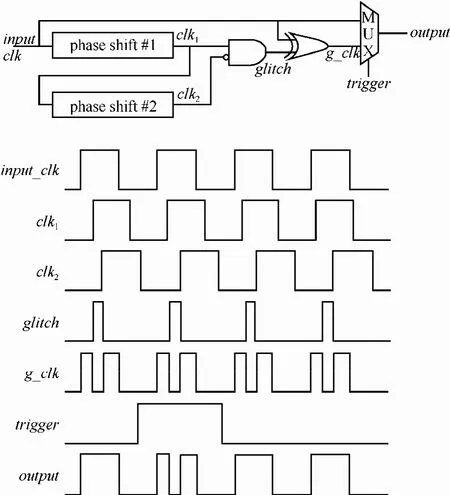
图12 时钟毛刺生成原理

2)时钟毛刺控制参数

为方便说明，对时钟毛刺的参数定义如下。

T：一个正常的时钟周期，为 280 ns（对应频率 3.57 MHz）。

Tt：trigger信号位置。

To：毛刺相对于trigger的偏置，通过调整这一参数可以灵活调整时钟毛刺的注入位置。

Gw：毛刺宽度，指毛刺信号中2个相邻上升沿之间的时间间隔。

3)时钟毛刺位置控制

实验中使用智能卡AUX1脚输出的trigger信号实现这一控制，当FPGA芯片检测到trigger信号上升沿时，FPGA中的计数器开始计数，计To个时钟周期后，将输入给智能卡的时钟信号切换为毛刺信号，并在添加一个毛刺时钟后切换为正常时钟信号。根据逆向推理验证，一个合适的毛刺信号通常只造成一个8位数据寄存器出现数据混淆，即产生一个单字节故障。To的值需要通过多次尝试和逆向推理验证来确定，为了能够在合适时机注入故障，本文通常将Tt设置在距离故障注入点较近的操作前，这样To的尝试范围将可以缩小到50 ns以内。

4)时钟毛刺宽度控制

为找到一个合适的毛刺宽度 Gw，对毛刺宽度和故障发生概率之间的关系做了进一步实验，下面以 PRESENT第28轮首个查找 S盒为例进行讨论。

实验令毛刺宽度Gw的值从95 ns开始，以0.56 ns为步长逐步减小，对每个 Gw值进行重复故障注入实验，统计故障发生概率。结果如图13所示,每点均对应270次故障注入的统计结果。

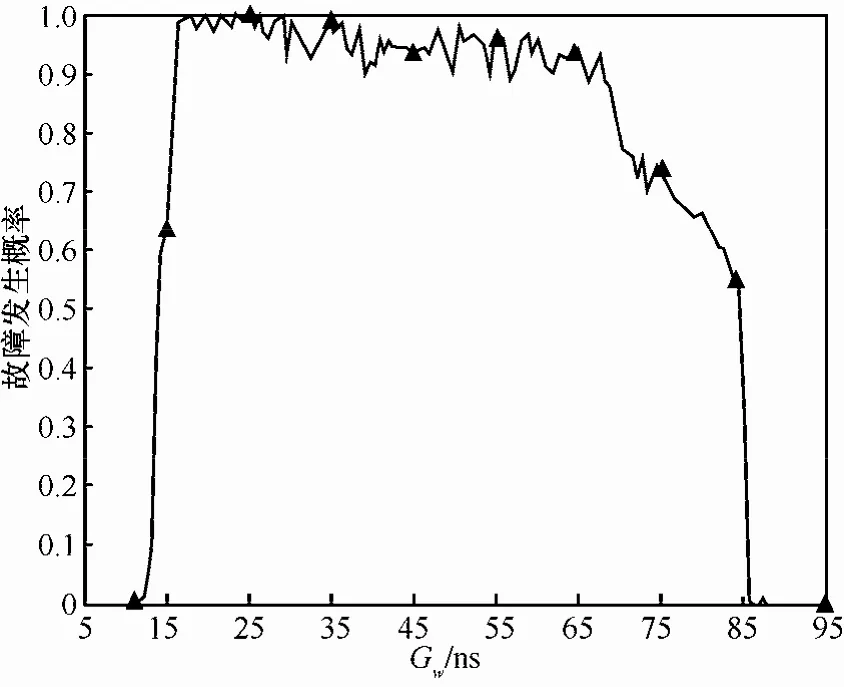
图13 故障频率与毛刺宽度的关系

由图13可知，当Gw从95 ns开始减小时，故障概率呈上升趋势，在Gw=85 ns时，故障概率增大，且随着Gw减小故障概率增加。16 nslt;Gwlt;82 ns对应的区间，由该时钟毛刺引导的故障概率接近100%。物理实验中，本文采用Gw=20 ns进行故障注入。下面介绍2种针对PRESENT-80的故障攻击实验。

5.3 基于字节模型的故障攻击

实验中设定Gw=20 ns，To取值为15～20时，可将故障注入到第28轮查找S盒，使查找S盒输出产生一个字节故障，如图 14所示。由于攻击针对的是PRESENT-80软件实现，结合简单功耗分析可识别出故障针对的字节索引，在Type B求解模式下执行了100次故障攻击实验，2次故障注入后80位主密钥剩余熵平均可被降低到8.07，攻击平均执行时间约为1 min。

图14 第28轮注入2次随机字节故障φ(K)统计

5.4 基于操作跳跃的故障攻击

在实验中，本文还发现，Gw=20 ns、To取值为13、14、24时，虽然从功耗曲线上可以看到8次查找8进8出大S盒的操作，但实际上该查找S盒操作被跳过去了，相当于注入了向8个S盒注入了差分为正确S盒输入和正确S盒输出异或结果的一个故障。实验中，故障注入到第30轮S盒计算过程中，首先使用1次故障注入样本在Type B求解模式下执行了100次攻击，PRESENT-80的密钥剩余熵可被降低到15～20。然后使用1次故障注入样本在Type A求解模式下执行了100次攻击，得到求解时间的统计分布，如图15所示。

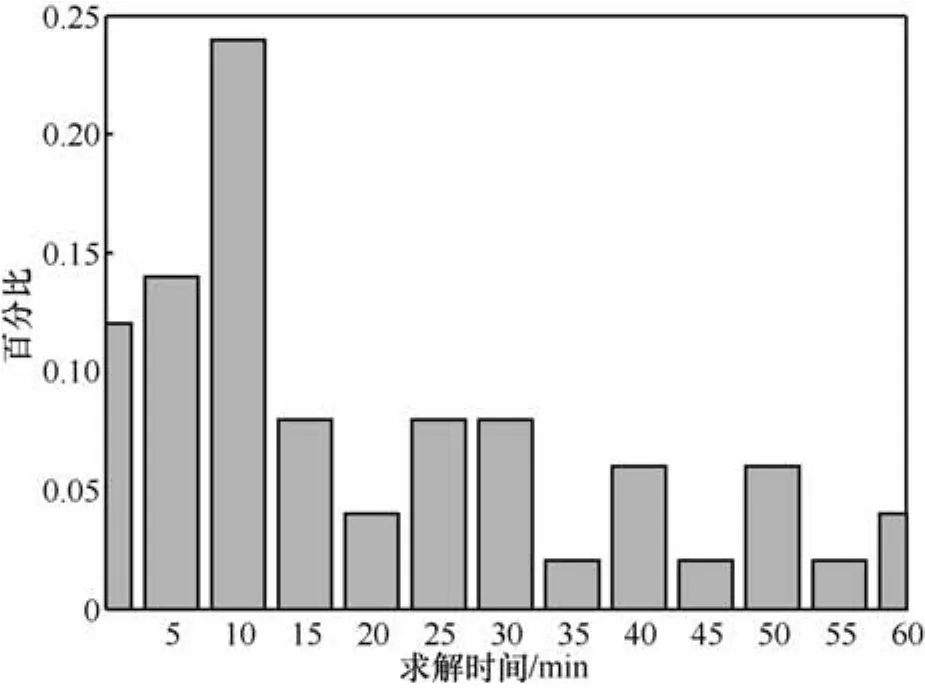
图15 第30轮注入1次查找S盒跳过故障后求解时间统计

由图15可以看出94%的情况下80位主密钥可在1个小时内求解出来。事实上，如果将求解时间放宽至6个小时，攻击成功率为100%。

6 结束语

提出了一种改进的基于代数分析的轻量级分组密码PRESENT算法代数故障分析方法，对其抗故障攻击能力进行了评估。结果表明，提出方法可建立十分紧凑的代数方程，挖掘所有的故障信息，得到更为准确的故障注入后的密钥剩余熵，攻击所需数据复杂度相比前人工作要低；同时，首次基于不同故障宽度、不同故障深度对PRESENT抗故障攻击能力进行了评估，并根据结果对已有故障攻击进行了解读和分析；最后对符合ISO/IEC 7816-3协议的智能卡上的PRESENT软件实现进行了基于时钟毛刺的故障注入实验，结果表明，如果第 28轮注入字节故障，2次故障注入可将主密钥剩余熵降低到8.07；如果第30轮注入跳过S盒计算故障，1次故障注入即可在94%的情况下、1个小时内恢复80位主密钥。

未来的工作主要有以下3个方面：1)结合硬件木马实现单位故障注入[23]，或对PRESENT的轮计数器打入故障[24]，有望在1次故障注入下恢复主密钥；2)开展基于故障不完美分布特征的故障攻击研究[25]，在唯错误密文场景下实现密钥恢复；3)开展PRESENT故障灵敏度分析研究[26,27]，攻破带有传统故障攻击防护的密码实现。

[1]BOGDANOV A,KNUDSEN L R,LEANDER G,et al. PRESENT: an ul-tra-lightweight block cipher[C]//CHES 2007. Vienna,Austria,c2007: 450-466.

[2]BOGDANOV A,LEANDER G,PAARC,et al. Hash functions and RFID tags: mind the gap[C]//CHES 2008. Washington,DC,USA,c2008: 283-299.

[3]WANG M. Differential cryptanalysis of reduced-round PRESENT[C]//AFRICACRYPT 2008. Casablanca,Morocco,c2008: 40-49.

[4]BLONDEAU C,NYBERG K. New links between differential and linear cryptanalysis[C]//EUROCRYPT 2013. Athens,Greece,c2013:388-404.

[5]BLONDEAU C,NYBERG K. Links between truncated differential and multidimensional linear properties of block ciphers and underlying attack complexities[C]//EUROCRYPT 2014. Athens,Greece,c2014:165-182.

[6]NAKAHARA J,SEPEHRDAD P,ZHANG B,et al. Linear (hull)and algebraic cryptanalysis of the block cipher PRESENT[C]//CANS 2009.Ishikawa,Japan,c2009: 58-75.

[7]CHO J Y. Linear cryptanalysis of reduced-round PRESENT[C]//CT-RSA 2010. San Francisco,CA,USA,c2010: 302-317.

[8]ALBRECHT M,CID C. Algebraic techniques in differential cryptanalysis[C]//FSE 2009. Leuven,Belgium,c2009: 193-208.

[9]BLONDEAU C,PEYRIN T,WANG L. Known-key distinguisher on full PRESENT [EB/OL]. http://eprint.iacr.org/2015/575.pdf,2015.

[10]ZHANG J,GU D W,GUO Z,et al. Differential power cryptanalysis attacks against PRESENT implementation[C]//ICACTE 2010. Chengdu,China,c2010: 661-665.

[11]李浪,李仁发,李肯立,等. 轻量级 PRESENT加密算法功耗攻击研究[J]. 计算机应用研究,2014,31(3),843-845.LI L,LI R F,LI K L,et al. Differential power analysis attacks on PRESENT[J]. Application Research of Computers,2014,31(3),843-845.

[12]RENAULD M,STANDAERT F X. Algebraic side-channel attacks[C]//In-scrypt 2009. Beijing,China,c2010: 393-410.

[13]ZHAO X J,GUO S Z,ZHANG F,et al. Efficient Hamming weight-based side-channel cube attacks on PRESENT[J]. The Journal of Systems and Software,2013,86: 728-743.

[14]LI J,GU D W. Differential fault analysis on PRESENT[C]//CHNA-CRYPT 2009. Guang Zhou,China,c2009: 3-13.

[15]WANG G,WANG S. Differential fault analysis on present key schedule[C]//CIS 2010. Nanning,China,c2010: 362-366.

[16]ZHAO X J,GUO S Z,ZHANG F,et al. Fault-propagate pattern based DFA on PRESENT and PRINT cipher[J]. Wuhan University Journal of Natural Sciences,2012,17(6): 485-493.

[17]GU D W,LI J R,LI S,et al. Differential fault analysis on light-weight block ciphers with statistical cryptanalysis techniques[C]//FDTC 2012.Leuven,Belgium,c2012: 27-33.

[18]吴克辉,赵新杰,王韬,等. PRESENT密码代数故障攻击[J]. 通信学报,2012,33(8): 85-92.WU K H,ZHAO X J,WANG T. Algebraic fault attack on PRESENT[J]. Journal on Communications,2012,33(8): 85-92.

[19]JEONG K,LEE Y,SUNG J,et al. Improved differential fault analysis on PRESENT-80/128[J]. International Journal of Computer Mathematics,2013,90(12): 2553-2563.

[20]KLOSE,D. PRESENT implementation[EB/OL]. http://www. lightweightcrypto. org/implementations.php,2011.

[21]郭世泽,王韬,赵新杰. 密码旁路分析原理与方法[M]. 北京：科学出版社,2014.GUO S Z,WANG T,ZHAO X J. Principles and methodologies of side-channel analysis in cryptography[M]. Science Press,Beijing,China,2014.

[22]ZHAO X J,GUO S Z,ZHANG F,et al. Improving and evaluating differen-tial fault analysis on LED with algebraic techniques[C]//FDTC 2013. Santa Barbara,CA,USA,c2013: 41-51.

[23]KUMAR R,JOVANOVIC P,BURLESON W P,et al. Parametric trojans for fault-injection attacks on cryptographic hardware[C]//FDTC 2014. Busan,Korea,c2014: 18-28.

[24]DEHBAOUI A,MIRBAHA A P,MORO N,et al. Electromagnetic glitch on the aes round counter[C]//COSADE 2013. Paris,France,c2013: 17-31.

[25]LI Y,HAYASHI Y,MATSUBARA A,et al. Yet another fault-based leakage in non-uniform faulty ciphertexts[C]//FPS 2013. La Rochelle,France,c2013: 272-287.

[26]LI Y,SAKIYAMA K,GOMISAWA S,et al. Fault sensitivity analysis[C]//CHES 2010. Santa Barbara,California,USA,c2010: 320-334.

[27]MORADI A,MISCHKE O,PAAR C,et al. On the power of fault sensitivity analysis and collision side-channel attacks in a combined setting[C]//CHES 2011. Nara,Japan,c2011: 292-311.

Improvement and evaluation for algebraic fault attacks on PRESENT

HUANG Jing1,ZHAO Xin-jie2,ZHANG Fan3,4,GUO Shi-ze2,ZHOU Ping5,CHEN Hao5,YANG Jian3

(1. Third Department of No.61541 Unit,Beijing 100083,China;2. The Institute of North Electronic Equipment,Beijing 100191,China;3. College of Information Science amp; Electrical Engineering,Zhejiang University,Hangzhou 310027,China;4. Science and Technology on Communication Security Laboratory,Chengdu 610041,China;5. Department of Information Engineering,Ordnance Engineering College,Shijiazhuang 050003,China)

An enhanced algebraic fault analysis on PRESENT was proposed. Algebraic cryptanalysis was introduced to build the algebraic equations for both the target cipher and faults. The equation set of PRESENT was built reversely in order to accelerate the solving speed. An algorithm of estimating the reduced key entropy for given amount of fault injections was proposed,which can evaluate the resistance of PRESENT against fault attacks under different fault models. Finally,extensive glitch-based fault attacks were conducted on an 8-bit smart card PRESENT implemented on a smart card.The best results show that only one fault injection was required for the key recovery,this is the best result of fault attacks on PRESENT in terms of the data complexity.

algebraic cryptanalysis,lightweight block cipher,fault attack,satisfiability solving,clock glitch

s:The National Basic Research Program of China (973 Program)(No.2013CB338004),The National Natural Science Foundation of China (No.61173191,No.61271124,No.61272491,No.61309021,No.61472357,No.61571063),The Fundamental Research Funds for the Central Universities (No.2015QNA5005),The Science and Technology on Communication Security Laboratory (No.9140C110602150C11053)

TP393

A

2015-07-15；

2016-01-13

国家重点基础研究发展计划（“973”计划）基金资助项目（No.2013CB338004）；国家自然科学基金资助项目（No.61173191,No.61271124,No.61272491,No.61309021,No.61472357,No.61571063）；中央高校基本科研专项基金资助项目（No.2015QNA5005）；保密通信重点实验室基金资助项目（No.9140C110602150C11053）

10.11959/j.issn.1000-436x.2016165

黄静（1983-），女，四川南充人，61541部队助理工程师，主要研究方向为卫星网络与信息安全。

赵新杰（1986-），男，河南开封人，博士，北方电子设备研究所工程师，主要研究方向为网络空间安全与密码学。

张帆（1978-），男，浙江杭州人，博士，浙江大学讲师，主要研究方向为密码旁路分析和故障分析。

郭世泽（1969-），男，河北石家庄人，北京电子设备研究所研究员，主要研究方向为网络空间安全与密码学。

周平（1988-），男，安徽无为人，军械工程学院博士生，主要研究方向为密码算法旁路分析与故障分析等。

陈浩（1987-），男，湖北武汉人，军械工程学院博士生，主要研究方向为密码算法旁路分析与故障分析等。

杨建（1991-），男，湖北武汉人，主要研究方向为分组密码代数故障分析。