对联接杂凑函数的“特洛伊”消息攻击

陈士伟，金晨辉

(1. 解放军信息工程大学三院，河南 郑州 450002；2. 信息保障技术重点实验室，北京 100072)

对联接杂凑函数的“特洛伊”消息攻击

陈士伟1,2，金晨辉1

(1. 解放军信息工程大学三院，河南 郑州 450002；2. 信息保障技术重点实验室，北京 100072)

“特洛伊”消息攻击是Andreeva等针对MD结构杂凑函数提出的一种攻击方法，首次将其应用于不同于MD结构的一类杂凑函数，即联接杂凑。结合联接杂凑的特点，综合利用Joux的多碰撞和深度为n−l的“钻石树”结构多碰撞，构造出了2n-bit联接杂凑函数的长度为 n⋅2k块的“特洛伊”消息，并据此首次提出了对其的固定前缀“特洛伊”消息攻击，其存储复杂性为 2 l + 2n−l+1+ n ⋅2k+1块消息，时间复杂性为 O( n ⋅ 2n+k+l⋅2l)次压缩函数运算，远低于理想的时间复杂性 O( n ⋅22n+k)。

杂凑函数；联接杂凑；“特洛伊”消息攻击；多碰撞；复杂性

1 引言

杂凑函数是密码学领域中一类重要的密码算法。它是将任意长度的消息转化成固定长度的二元字符串的一类函数，杂凑的结果称为杂凑值或摘要。若杂凑值的规模为n bit，则称其为n-bit杂凑函数。一个杂凑函数 H(M)需要满足以下 3条基本的安全性原则。

1)抗碰撞性：找到满足 H( M1)=H( M2)的一对碰撞消息在计算上是不可行的。

2)抗原像性：对于给定的杂凑值h，找到满足H( M )=h的消息M在计算上是不可行的。

3)抗第二原像性：对于给定的消息M1和对应的杂凑值 h=H( M1)，找到另一个消息 M2≠M1，使H( M2)=h在计算上是不可行的。

杂凑函数的安全强度取决于杂凑值的规模，对于一个n-bit杂凑函数，如果找到产生相同杂凑值的一对碰撞消息的时间复杂性低于，或找到给定杂凑值的原像（或第二原像）的时间复杂性低于2n，则称该杂凑函数是可破的。

杂凑函数主要包括2部分，即压缩函数和迭代结构，其中，迭代结构是迭代压缩函数的一种变换方式，比如杂凑函数 MD5、SHA-0等所用的迭代结构是强化的Merkle-Damgard[1,2]（简称MD）结构。通常情况下，密码学者们在压缩函数是随机函数或满足某些性质的条件下，分析迭代结构的安全性，这类分析方法称为对杂凑函数的一般攻击。Merkle[1]和 Damgard[2]在压缩函数满足抗碰撞的条件下，证明了强化MD结构也是抗碰撞的，因此它在最初的杂凑函数设计中是最常用的一种迭代结构。然而，在假定压缩函数是随机函数的条件下，Joux[3]构造出了MD结构杂凑函数的2k-碰撞，即2k个不同的消息产生相同的杂凑值，其时间复杂性约为低于理想值之后，Kelsey和Schneier利用可扩展消息提出了对具有MD结构的杂凑函数的长消息第二原像攻击[4]，又利用“钻石树”结构提出了对其的选择目标强制前缀攻击（即“牧群”攻击）[5]。2011年，陈士伟等[6]提出了对强化MD结构的改进“牧群”攻击。在这些对MD结构杂凑函数的有效攻击被提出的同时,密码学者们也开始尝试着分析并设计一些不同于MD结构的迭代结构。2009年，Andreeva等[7]基于 Joux的−多碰撞构造出了深度为l的“钻石树”结构的方法，其时间复杂性约为并利用该方法将“牧群”攻击应用于联接杂凑、二次杂凑等与MD结构不同的其他迭代结构，进一步地将其转化为第二原像攻击。与此同时，他们提出了一种新的攻击方法——“特洛伊”消息攻击，但仅将其应用于 MD结构杂凑函数。2013年的亚密会上，Kortelainen T等[8]提出了构造n-bit杂凑函数的深度为d的“钻石树”结构的新方法，其时间复杂性约为并提出了对MD结构杂凑函数的 2类改进的“特洛伊”消息攻击。但是，迄今为止，没有文献提出对具有不同于MD结构的迭代结构的杂凑函数的“特洛伊”消息攻击。

联接杂凑是不同于MD结构的一种迭代结构，它利用2个不同的杂凑函数对输入消息进行杂凑，然后将2个杂凑的结果联接作为杂凑值输出，这是提高杂凑函数安全强度的一个简单又有效的设计思想。本文将综合利用“钻石树”结构、Joux的多碰撞等多种技术，构造出2n-bit联接杂凑的长度为 2kn⋅ 块的“特洛伊”消息，并据此提出对其的“特洛伊”消息攻击，其时间复杂性约为存储复杂性为块消息。

2 基本概念

下面介绍联接杂凑函数和“特洛伊”消息攻击的相关概念。

2.1 联接杂凑函数

首先给出MD结构杂凑函数的概念。

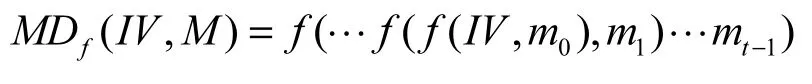
就联接杂凑函数而言，对于任意的输入消息，它是将2个基于不同压缩函数的MD结构杂凑函数的杂凑结果联接之后作为杂凑值输出。下面给出2n-bit联接杂凑函数 ConHFf1,f2的具体描述。

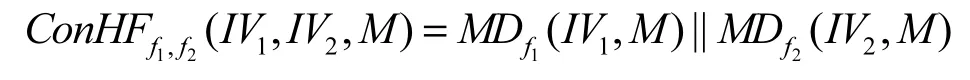
2.2 “特洛伊”消息攻击

2009年，Andreeva等[7]提出了对杂凑函数的一种新的一般攻击方法，即“特洛伊”消息攻击，它本质上是一类第二原像攻击。其基本的攻击思路是首先攻击者A构造一个“特洛伊”消息S并提供给受害者V，V从一个限定的集合中任意选择前缀P构成消息P||S传递给A。由于“特洛伊”消息 S是由攻击者A构造的，故如果S能够满足一些特定的性质，则A就可以成功地给出消息P||S的一个第二原像。针对MD结构杂凑函数H，Andreeva等给出了以下2类“特洛伊”消息攻击。

1)碰撞−“特洛伊”攻击：在S中引入一个限定的改变产生S′，使

2)牧群−“特洛伊”攻击：在S几乎不发生改变的条件下，找到 P′和 S′，使

2013年，Kortelainen T等[8]利用“钻石树”结构和可扩展消息技术提出了对MD结构杂凑的改进版本的“特洛伊”消息攻击，即弱“特洛伊”攻击和强“特洛伊”攻击，其时间复杂性明显低于文献[5]中的攻击方法。

然而，迄今为止，并没有文献对联接杂凑抵抗“特洛伊”消息攻击的能力进行分析。

3 对联接杂凑函数的“特洛伊”消息攻击算法

“特洛伊”消息攻击中最关键的步骤在于“特洛伊”消息的构造。“特洛伊”消息的成功构造可以保证在攻击过程中只需改变“特洛伊”消息的小部分比特，即可给出原消息的第二原像。而由联接杂凑的描述可知，它是利用2个不同的MD结构杂凑函数对同一消息进行杂凑，并将杂凑的结果联接后输出，故构造出的“特洛伊”消息应该在2条杂凑路径上保持一致。下面将利用Joux的多碰撞技术和“钻石树”结构多碰撞技术提出对联接杂凑的固定前缀的“特洛伊”消息攻击，即对给定的单块前缀 Pre，找到P′和S′，使并对该攻击算法的计算复杂性进行分析。

3.1 算法描述

对联接杂凑函数的固定前缀“特洛伊”攻击分2个阶段，即“特洛伊”消息构造阶段和固定前缀的第二原像攻击阶段。在“特洛伊”消息构造阶段，为了保证“特洛伊”消息在2条杂凑路径上保持一致，首先在第 1条路径上构造长度为的多碰撞，然后以此多碰撞为基础构造出深度是n−l的“钻石树”结构。接着，构造出长度为n的多碰撞，然后在2n个多碰撞消息中选择出1个使2条路径上的消息一致。在固定前缀的第二原像攻击阶段，已构造的具有2n−l个起始点的“钻石树”结构多碰撞和长度为 l的多碰撞使能够成功找到产生相同杂凑值的第二原像。下面给出算法的具体描述（如图1所示）。

1)第1阶段：“特洛伊”消息构造阶段

Step1在第1条杂凑路径上,以IV1为初始值，计算并以ha为起始点，利用文献[3]中 Joux的方法构造长度为块的多碰撞，产生的最终链接变量记为hb。

Step2在第2条杂凑路径上，以IV2为初始值，计算随机选择2n−l个起始点，基于第 1条杂凑路径上的长为的多碰撞，构造出深度为n−l的“钻石树”结构，产生的最终链接变量记为

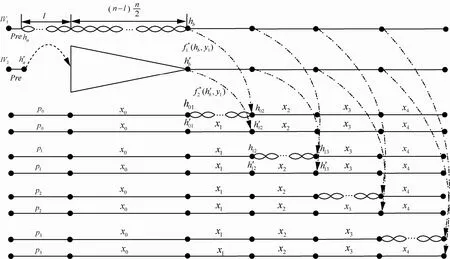
图1 对联接杂凑函数的固定前缀“特洛伊”消息攻击

Step3选择长度为块的一个值x0，并计算，以链接变量h01为起始点，构造一个长度为n块的多碰撞，产生的最终链接变量记为h02。

Step4搜索长度为n块的一个值y1，使

Step5记由于对任意元素和固定的初始值 h，故从Step3构造出的长度为n块的多碰撞中的 2n个消息中一定能够找到一个消息x1使则有

Step6类似于 Step3～Step5，找到满足条件的第 i个消息xi，即：记在第1条杂凑路径上，以h(i−1)i为起始点，构造长度为n块的多碰撞，产生的最终链接变量记为；搜索长度为n块的消息yi使在第2条杂凑路径上，从第1条杂凑路径上产生的n块长多碰撞中的2n个消息中找到一个消息xi使则有

Step7依此类推，直至找到 2k个具有类似性质的消息

Step8输出“特洛伊”消息

2)第2阶段：输出第二原像阶段

Step1以为初始值，从第1阶段的Step1中构造的长度为 l块的多碰撞中选择消息，使等于“钻石树”的2n−l个起始点中的一个，并在“钻石树”结构多碰撞中找到以此为起始点的消息M0。

Step2输出消息则

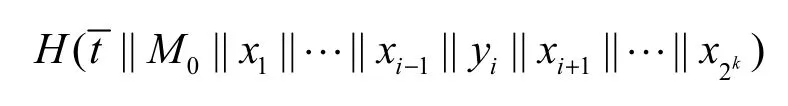
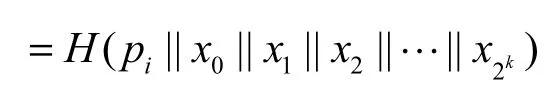
3.2 算法复杂性分析

下面分2个阶段给出联接杂凑的“特洛伊”攻击的时间复杂性和存储复杂性分析结果。

1)第1阶段

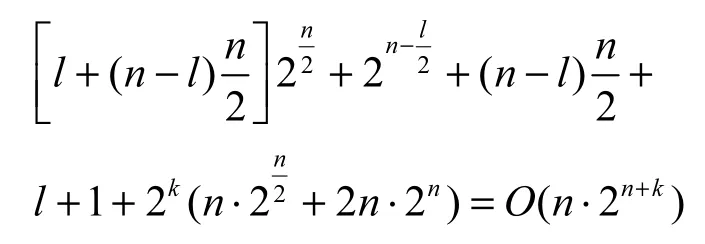
在Step1和Step2中，需存储长为l块的多碰撞和深度为n−l的“钻石树”结构，共块消息；Step5～Step7中，需存储2k对长度为n的消息对共块消息，故第1阶段的存储复杂性为

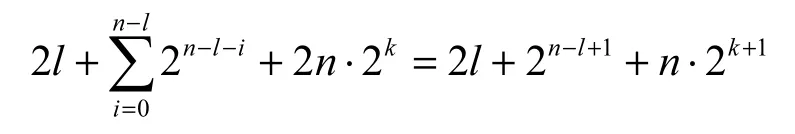
2)第2阶段

Step1所需的时间复杂性为 2ll⋅次压缩函数运算，且Step2的时间复杂性可忽略不计，故第2阶段的时间复杂性为 2ll⋅，存储复杂性可忽略不计。

综合2个阶段的分析结果可知，对联接杂凑的固定前缀的“特洛伊”攻击的时间复杂性约为次压缩函数运算，存储复杂性约为块消息。由于“特洛伊”攻击给出的第二原像的长度块,故找到杂凑值规模为2n bit的联接杂凑的相同长度的第二原像的理想计算复杂性为次压缩函数运算，约为本文给出的“特洛伊”消息攻击所需时间复杂性的2n倍。

4 结束语

本文通过分析联接杂凑函数的特点，综合利用Joux的多碰撞和“钻石树”结构多碰撞，首次提出了对联接杂凑函数的固定前缀“特洛伊”消息攻击，其存储复杂性为 2l + 2n−l+1+ n ⋅2k+1块消息，时间复杂性为 O( n ⋅ 2n+k+l⋅2l)次压缩函数运算，远低于理想的时间复杂性。这说明联接杂凑函数不能抵抗“特洛伊”消息攻击。

[1]MERKLE R. A certified digital signature[C]//Advances in Cryptology-CRYPTO 1989. LNCS 435,Heidelberg: Springer-Verlag,c1990:218-238.

[2]DAMGARD I. A design principle for hash functions[C]//Advances in Cryptology-CRYPTO 1989. LNCS 435,Heidelberg: Springerr-Verlag,c1990: 416-427.

[3]JOUX A. Multicollisions in iterated hash functions application to cascaded constructions[C]//Advances in Cryptology–CRYPTO 2004.LNCS 3152,Heidelberg: Springer-Verlag,c2004: 306-316.

[4]KELSEY J,SCHNEIER B. Second preimages on n-bit hash functions for much less than 2nwork[C]//Advances in Cryptology- EUROCRYPT 2005. LNCS 3494,Heidelberg: Springer-Verlag,c2005: 474-490.

[5]KELSEY J,KOHNO T. Herding hash functions and the nostradamus attack[C]//Advances in Cryptology–EUROCRYPT 2006. LNCS 4004,Heidelberg: Springer-Verlag,c2006: 183-200.

[6]陈士伟,金晨辉. 对强化MD结构杂凑函数的一个新的“牧群”攻击[J]. 电子与信息学报,2010,32(8): 1953-1955.CHEN S W,JIN C H. A new herding atlack on hash functions with strengthening Merke-Damgard(MD)construction[J]. Journal of Electronics amp; Information Technology,2010,32(8): 1953-1955.

[7]ANDREEVA E,BOUILLAGUET C,DUNKELMAN O,et al. Herding,second preimage and Trojan message attacks beyond Merkle-Damgård[C]//Selected Areas in Cryptography 2009. LNCS 5867,Heidelberg: Springer-Verlag,c2009: 393-414.

[8]KORTELAINEN T,KORTELAINEN J. On diamond structures and Trojan message attacks[C]//Advances in Cryptology–ASIACRYPT 2013,Part II,LNCS 8270. Heidelberg: Springer-Verlag,c2013: 524-539.

Trojan message attack on the concatenated hash functions

CHEN Shi-Wei1,2,JIN Chen-Hui1

(1. The Third College,PLA Information Engineering University,Zhengzhou 450002,China;2. Science and Technology on Information Assurance Laboratory,Beijing 100072,China)

The Trojan message attack was proposed by Andreeva,et al. aiming at the hash functions with MD structure.First it was applied on the hash function beyond MD structure,that was,concatenated hash. Utilizing the property of the concatenated hash,and combining the Joux’s multicollision and the “diamond” structure with the depth of n−l,a Trojan message of the length n⋅2kblocks for the 2n-bit concatenated hash was constructed,based on which a chosen-prefix Trojan message attack was first proposed. And the memory complexity of proposed attack is about 2 l + 2n−l+1+n ⋅2k+1blocks and the time complexity is about O( n⋅ 2n+k+l⋅2l)computations of the compression function,much less than the ideal value O( n ⋅22n+k).

hash functions,concatenated hash,Trojan message attack,multicollsion,complexity

The National Natural Science Foundation of China(No.61272041)

TP918

A

2015-09-08；

2016-05-31

国家自然科学基金资助项目（No.61272041）

10.11959/j.issn.1000-436x.2016154

陈士伟（1983-），女，河南唐河人，解放军信息工程大学讲师，主要研究方向为对称密码算法分析。

金晨辉（1965-），男，河南扶沟人，解放军信息工程大学教授，主要研究方向为密码学与信息安全。