主动式复杂事件处理方法的研究
耿少峰,王永恒,李仁发,张佳
(1. 湖南大学信息科学与工程学院,湖南 长沙 410082;2. 集美大学计算机工程学院,福建 厦门 361021)
主动式复杂事件处理方法的研究
耿少峰1,2,王永恒1,李仁发1,张佳2
(1. 湖南大学信息科学与工程学院,湖南 长沙 410082;2. 集美大学计算机工程学院,福建 厦门 361021)
在CPS的应用背景下,对传感器和控制设备产生的不确定性事件流进行分析和处理得出高层事件,然后在此基础上引入适应性动态贝叶斯网络和并行马尔可夫决策过程模型来支持主动式的复杂事件处理。针对大型CPS中马尔可夫决策过程存在的状态数量巨大的问题,引入状态划分和报酬分解的方法来进行并行优化。在模拟交通网络的环境中,实验结果显示所提方法能有效地处理事件流,并具有良好的可扩展性。
信息物理融合系统;大数据;复杂事件处理;马尔可夫决策过程
1 引言
信息物理融合系统(CPS, cyber physical system)将智能计算、通信和控制技术深度融入到物理系统,使计算资源与物理资源紧密结合与协调分配,完成信息世界与物理世界的融合。它的应用领域非常广泛,小到智能家庭网络,大到工业控制系统,覆盖了各种不同规模的应用系统。如何有效地处理 CPS应用中所产生的大数据是人们目前需要面对的主要问题。当前在大数据研究领域,对于历史数据的分析和处理已经进行了广泛深入的研究,特别是在数据仓库和数据挖掘方面。常用方法之一是将大量的服务器组成集群或使用专业的云计算平台(如亚马逊的AWS)以及基于Hadoop的分布式计算框架。另外一种近期常见的计算平台是Spark,它突破了 MapReduce的算法框架,支持更灵活的数据处理方式,性能也有了很大的提升。但这些方式并不适合于 CPS的数据处理。因为 CPS在工作时产生的是实时的数据流,对这些数据流的处理往往有较高要求的时间约束。而 Hadoop/MapReduce的计算框架仅适用于处理静态数据和历史数据。近期也出现了一些面向数据流的处理平台,如Spark streaming、Storm和Flink。这些平台能够高效地处理数据流,但仅限于比较简单的过滤、聚合等操作,无法直接支持面向CPS的复杂数据流处理。
在 CPS应用中,系统必须处理来自无线传感网、RFID阅读器、GPS、社会媒体等各种各样设备的信号,这些信号可以被当成事件来处理。这些由设备直接生成的事件称为原始事件。一般情况下原始事件里的语义信息非常有限,在实际应用中,人们更加关注的是业务逻辑和规则等高级别信息。如在装有智能门禁的小区门口有车辆通行时,RFID阅读器会进行读操作来生成原始的事件,但只有“车辆进入或离开小区”这样的复杂事件才是人们真正关心的,可以根据一些模式将许多原始事件结合在一起,从而得到对用户有意义的复杂事件。CPS应用系统先将业务逻辑转换成复杂事件,再通过处理复杂事件来检测业务逻辑。复杂事件处理(CEP,complex event processing)[1]用于处理数量巨大的简单事件,并从中得到有价值的高层次的信息。
在某些CPS的应用中,对象执行的操作可以改变系统的状态。当前主流的事件处理方法为响应式的,这意味着动作是由系统状态发生变化触发。主动式事件处理系统通过运用预测和自动决策技术[2]减轻或避免将来不希望的事件发生。例如,在一个CPS的交通网络中,可以根据当前的状态和历史数据来预测道路的拥挤状态,然后采取一些行动以避免将来可能出现的拥堵。马尔可夫决策过程(MDP,Markov decision process)作为一个最佳决策过程中的随机动态系统,多年来人们已对其进行了深入的研究,并在多个领域中得到了广泛的应用。
目前,基于MDP实现主动式复杂事件处理还面临着巨大的挑战。首先是如何有效地处理由于误读、干扰等原因产生的事件的不确定性。当前的研究主要限于通过信息融合和推理来解决单个事件的不确定性,但缺乏对复杂事件不确定性的研究。另一个问题是如何进行高效准确的状态预测。尽管人们已经对数据流预测进行了大量的研究,但针对CPS产生的高速、海量数据流,预测模型和算法上都还面临挑战。同时,在决策支持方面,目前很少有文献涉及如何将MDP融入到主动式复杂事件处理中,以及如何应对在此过程中MDP所产生的巨大的状态空间。
针对上述问题,本文提出一种主动式复杂事件处理的架构和方法。该方法以交通网络为背景,将树的匹配和缓冲链表相结合,高效地处理了大量由车辆产生的不确定事件流,然后将处理后的复杂事件提交给适应性动态贝叶斯网络(ADBN, adaptive dynamic Bayesian network)来预测未来事件和系统状态,最后主动式响应器根据 ADBN的预测结果,利用一种基于状态划分和并发操作的新型并行MDP方法进行分析,最终产生避免交通拥堵的决策。
2 相关研究
CEP通过监测不断产生的数据流,根据每个事件发生的集合/序列识别复杂事件,然后对检测到的状态做出回应。Etzion等[3]在其著作中定义了复杂事件处理的基本概念及体系结构。一个事件处理agent(EPA, event processing agent)执行某些处理逻辑,从输入事件中提取出复杂事件。多个EPA连接在一起可以执行更复杂的层次化事件处理,这种网络称为事件处理网络。
在以前的主动数据库研究中,人们已经对 CEP做了大量的工作。常用的方法都是基于固定的数据结构,如树、图、自动机和 Petri网。这些方法很难灵活地对事件查询语言的实现进行优化,也很难根据应用需求的变化来支持查询语言的扩展。针对这些问题,Eugene等[4]提出了一种基于查询规划的复合事件检测方法(SASE)。SASE基于有限自动机(NFA)和堆栈来检测复杂事件,并对大的滑动窗口和大的中间结果集进行了优化,实现了比较好的性能和可扩展性。近年来的很多工作围绕着对SASE的改进展开,AGRAWAL等[5]提出了改进的有限状态机模型来提供更丰富的查询能力,Zhang等[6]对SASE进行了改进,提供了对非精确时标的事件流的支持。
由于传感器噪声等因素,CPS事件具有不确定性,这种不确定性通常使用概率来表示。处理概率性原始数据的CEP普遍采用的模型有隐马尔可夫模型、动态贝叶斯网络和条件随机域等。近年来也出现了一些基于有限状态机的概率复杂事件处理方法。文献[7]基于NFA设计了一种新的数据结构——链接实例队列(chain instance queues),并采用一种条件概率索引树来提高搜索性能。另外,文献[8]面向NFA提出一种优化方法,不仅能够计算复杂事件的概率,还能够对不可信网络产生的数据获取复杂模式的可信度。基于有限状态机的概率复杂事件处理,比较有代表性的研究项目是美国华盛顿大学的Cascadia系统[9]和Laha系统[10]。Cascadia系统基于概率数据库中的可能世界模型(possible world model),实现了对概率事件流和历史概率事件的查询,但没有在预处理中考虑流上相邻事件间的时间关联性。Laha成功支持了关联概率事件流上的高效查询,并支持更复杂的事件代数操作,从而能支持更灵活的复杂事件处理。
主动式系统的研究已经持续了多年,如主动式运输管理系统[11]、面向即时无线网络的主动型路由[12]等。这些研究总体上代表了一种由响应式系统向主动式系统转变的潮流。在复杂事件处理这个领域,对主动式方法的研究还比较少。但当前CPS的发展已经对这种研究提出了需求,也提供了研究的基础条件。Engel等[13,14]提出了一种基于事件的主动式计算框架,该框架主要由复杂事件处理网络、预测器和基于马尔可夫决策过程的主动式响应器构成。该工作对传统的复杂事件处理agent进行了扩展,支持2种新型的agent:预测agent用于预测系统状态;主动式响应agent用于计算合适的响应并执行。但它的应用背景不是面向CPS,也没有考虑大规模的数据和状态的问题。
多年来,人们对MDP进行了广泛的研究和应用,产生了多个变种。对于大型CPS应用这个领域,最大的挑战在于巨大的状态空间造成的组合爆炸问题。对这个问题当前主要有2个研究方向。第一类是根据问题领域中的信息来简化结构,如状态聚集的方法[15]和时间聚集的方法[16]等。此类方法的问题和具体的系统相关,无法找到普遍的解决方法。第二类是近似计算的方法,如近似动态规划[17]和选择性近似[18]等方法。这类方法的关键是如何在优化过程中对值函数进行近似。当应用到大型CPS的事件处理领域,MDP的规模更大且具备一些新的特征,其具体模型和大规模计算问题的解决仍然是一个挑战。

图1 系统架构
3 系统架构
本文方法的总体结构如图1所示。CPS中各类传感器及RFID等设备产生的信号,汇聚在一起称为原始事件流。由于设备本身的精度及干扰等原因,这些事件不是完全精确的,称为概率事件。这些原始事件经过概率复杂事件处理引擎的处理,提取出有意义的高层事件,也就是复杂事件。其中,PEPA(probabilistic event processing agent)为概率事件处理器[19],它负责处理由底层设备产生的原始事件流,并最终生成概率复杂事件。查询规划器根据复杂事件查询语句使用一个或多个 PEPA来完成查询。多个 PEPA组合在一起构成的网络称为概率事件处理网络(PEPN, probabilistic event processing network)。本系统中预测分析器(PA, predictive analytics)的实现方法是基于Pascale等[20]的工作,通过使用一种适应性动态贝叶斯网络模型,根据输入的复杂事件来预测道路网络中可能会发生拥堵的节点。复杂事件被存储在事件数据库中,PA可以通过学习这些历史事件获得更准确的预测。主动式响应器根据 PA预测出来的系统未来状态,利用并行MDP产生避免或减弱这些状态发生的决策。PRA(proactive agent)为执行器,负责执行对应的决策动作。上下文可以从复杂事件中获取,也可以从其他信息系统获取,并影响系统的状态预测和控制。
定义1 概率原始事件CPS事件流中的原始事件即在某个时间的一次发生(一次信号读取)。概率原始事件表示为:lt;ID, A, T, Prgt;。其中,ID为产生数据的设备标签号,A为事件属性的集合,T为事件发生的时标。Pr为事件发生的概率值,它代表由原始信号转换为确切的CPS事件的概率。
定义 2 概率复杂事件是由原始事件或者复杂事件按照一定的运算规则形成的事件。一个概率复杂事件表示为:lt;E, R, Tc, Prgt;。其中,E是符合合成规则的概率原始事件串,R为事件合成规则,Tc为事件的时间跨度,Pr为事件概率值。
事件类型由一组具有相同语义和结构的事件规则构成,每个事件对象都是一个事件类型的实例。一个事件类型可以表示为原始或复杂事件。主要的复杂事件模式包括 ALL、ANY、COUNT和SEQ[3]等。如在交通系统中,COUNT模式用来计算规定时间内某一地点经过车辆的数量。把这些模式结合起来可以构建层次性的复杂模式。
4 主动式复杂事件处理
4.1 不确定性事件流的处理方法
由于RFID阅读器等设备存在漏读、误读和脏读等情况,所以导致交给PEPA处理的数据存在不确定的可能性。这些不确定的原始数据被称为不确定事件。不确定事件流的复杂事件处理主要有2个挑战,一是如何对大量高速的、实时的事件进行符合查询规则的检测;二是如何计算由相关或不相关的不确定事件流组成的复杂事件的概率。本文提出了一种面向不确定性事件流的复杂事件处理方法(ISCEP, indeterminate stream complex event processing)来解决上述问题。该方法采用事件概率模型建模,并通过基于匹配树与各节点的缓冲链表相结合的方法来处理大量的事件流。
在大规模的 CPS应用中经常需要处理分布式的事件流,本文假设不同事件流上的事件实例是相互独立的。在单一事件流里,一些在SEQ模式中的原始事件具有马尔可夫性。这意味着下一个事件发生的概率仅取决于序列中的当前事件,和历史事件无关。如一辆汽车在i+1时刻的位置和它在i时刻的位置有关,而和i时刻之前的位置无关。一个具有马尔可夫性的事件序列被称为马尔可夫链。像Kawashima等[9]做的工作那样,使用条件概率表(CPT)来处理条件概率。除了这些马尔可夫链的事件,可能还存在一些相互独立的原始事件。对于一个SEQ事件E=SEQ(e1, e2,…,en),原始事件划分为2个集合S和T。S包含相互独立的事件,T包含一个或多个马尔可夫链。SEQ事件的概率可以根据式(1)计算。
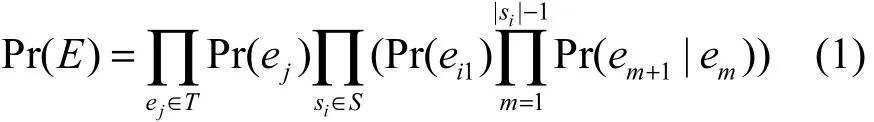
其中,Si是非独立集合 S中的某一条马尔可夫链,e1表示马尔可夫链中的第一个事件,Pr(em+1|em)表示连续发生的事件是前后相关的,它的值可以在CPT中获得。
事件概率模型中PEPA的输入是由概率原始事件组成的事件流。阅读器所处区域用大写字母表示,时标用数字表示。如图2所示的阅读器在不同区域和时刻读取到由同一个设备产生的概率流。

图2 概率原始事件流
EPA的输出是概率复杂事件。例如表1是经过处理后得到的某个车辆可能的行驶路径,其中省略了复杂事件的合成规则和时间跨度,保留了2个主要的属性:符合合成规则的概率原始事件串和复杂事件的概率。根据EPA的输出,PA可以选择更可靠的结果作为输入,这样在一定程度上可以避免因数据错误而导致错误的状态预测。

表1 概率复杂事件输出流
不确定性事件流的具体处理流程如图3所示。

图3 不确定性事件流处理方法
当查询被提交的时候,会注册相应的复杂事件。所谓注册就是在查询映射表中建立查询索引,同时建立用于流处理的匹配树。将交通网络划分为若干子区域,根据子区域和不同的时间段(如早晚高峰期)对应的已注册查询来构建查询映射表。当某一时段内某个区域发生事件的时候,就可以通过查询映射表迅速地找到已注册查询。如构造一个如表 2所示的查询映射表。如果从输入流中读取到8:00区域A在发生事件,那么应该将原始事件发送到查询1对应的匹配树处理。

表2 查询映射表
当处理实时数据流时,每个登记的查询都会建立一个匹配树。基本的建立规则在文献[21]描述。叶子节点是区域节点,中间节点是复合规则节点。在每一个节点的下方都会建立一个缓冲链表用以缓冲历史事件。如图4所示是查询1的匹配树构造结果,其中,SEQ节点是由B、C区域事件节点组成,TSEQ节点是由复合节点SEQ和A区域事件节点组成。
在执行查询时,首先获得概率简单事件流中的每一个区域事件的相关查询集合。接着遍历每一个查询,把区域事件输送到查询对应匹配树中,按照自底向上的方式进行匹配。如果当前节点匹配成功就会在本节点的缓冲链表中加入匹配成功的记录,接着发送更新消息给父节点。父节点接到更新消息就会对所有子节点的缓冲链表进行匹配,若满足规则会在自己的缓冲链表中加入成功匹配的节点记录,然后继续向上级节点发送更新消息。如此迭代直到没有节点再接收到更新消息为止。最后对匹配树的根节点缓冲链表进行查看,如果有成功匹配记录,则自顶向下输出所有过程并返回结果集合,否则直接结束。具体过程如算法1所示。
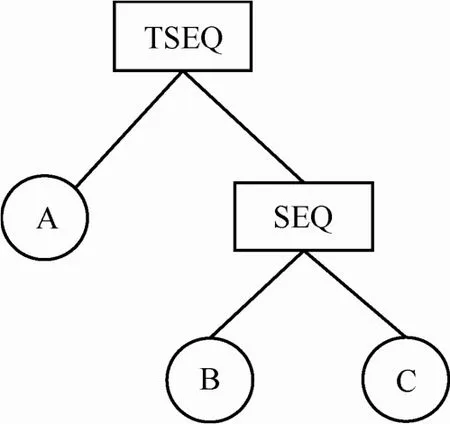
图4 查询1的匹配树
算法1 ISCEP算法
输入 E为概率原始事件流,QTree为查询匹配树
输出 R为概率复杂事件模式的实例集合
方法:


算法中几个函数含义如下。
Add():事件匹配成功后,将记录加入链表。记录包含新计算的复杂事件概率、产生此记录的事件集合和时标。
Update():节点缓冲链表有新记录加入后,用此函数向节点的父节点发送更新消息。
Match():对子节点缓冲队列中的记录按照时标顺序由后往前进行遍历,对时标限制和运算符限制进行匹配。
Output(QTree):根节点缓冲链表有记录时候调用。因为成功匹配记录包含直接子节点的信息,所以按照自顶向下的方式检索直到叶子节点,就能得到组成当前查询结果的所有信息。
设已注册的查询有N个,表示为Q1,…,QN,划分的区域有M个,表示为D=D1,…,DM,函数f(Di)表示区域Di对应的查询的集合。设一个新的查询Q对应K个区域,表示为DQ=DQ1,…,DQK,其中,DQi∈D。在没有优化的情况下,Q的查询代价表示为,QDi表示对应到区域 DQi上的子查询。如果某个区域DQi上的子查询和已注册查询匹配,则其代价可表示为find(f(DQi))+ merge(f(DQi)),其中,merge(f(DQi))为合并子查询结果的代价,而由于建立了索引,find(f(DQi))可忽略不计。设已注册查询匹配率为 α,则查询 Q的区域匹配数为对应的区域集合为D'Q。则Q的查询代价变为。由于merge合并结果的代价远小于直接查询,因此当匹配率α的值比较大的时候,算法的查询性能会有大幅度的提高。
4.2 基于并行马尔可夫决策过程的决策方法
针对CPS复杂事件处理系统的特点,传统马尔可夫决策过程扩展如下。
定义 3 主动式复杂事件系统并发马尔可夫决策过程。一个主动式复杂事件系统并发马尔可夫决策过程定义为。其中,I为处理动作的agent有限集合,S为状态的有限集合,包含一个特殊的初始状态为动作联合,其中,Ai为来自第 i个 agent的动作。P: S×A×S→[0, 1]为状态转换函数,P(s,α,s')代表在状态 s执行响应 α后转换到状态 s'的概率,R:S→Re为报酬函数(Re为实数)。对每个为CPS的复杂事件,复杂事件的变化影响系统的状态。C为上下文,在不同的上下文中,agent会采用不同的动作为复杂事件对系统状态的影响。
系统从原始状态开始,根据合适的策略选择一个或多个动作,由动作agent执行。动作agent的操作引起 CPS原始事件的变化,原始事件的变化引起复杂事件的变化,根据对复杂事件的综合分析,确定系统转移到下一个状态的概率。马尔可夫决策过程的关键是寻找一个策略π :S→A,它把每个状态映射到一个动作集合。最优的策略使报酬的总和达到最大。策略选择步骤基于式(2)。

策略更新步骤基于式(3)。
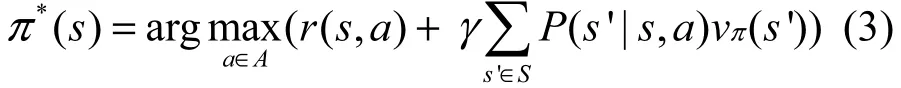
其中,γlt;1为衰减因子。经典的MDP中动作是顺序执行的,最近有些研究提到并发MDP按功能对不同的动作进行分组,这些分组后的动作并发执行且相互没有影响。MDP模型针对一个状态有多个并发执行的动作,它们在不同的位置执行相同的功能来协同把系统转向期望的状态。本文中的MDP方法基于以下观察结果。
1) 观察结果1。大型CPS中的对象可以根据上下文进行划分,每个组对应一个子状态,而不单独考虑每个对象的状态。
例如在考虑交通拥堵问题时,每个路口的车流量(或拥堵情况)是子状态,所有路口的拥堵状况构成系统的总体状态。
2) 观察结果2。大型CPS中某个位置对应的子状态依赖于其邻居位置的状态(此处的邻居是指在一定范围内和当前节点相连的其他节点)。
例如某个路口的拥堵状态依赖于前一个时间段其邻居路口的拥堵状态。
3) 观察结果3。在大型CPS中,可以把状态节点分为一般节点和重点节点。重点节点是在主动式处理中要控制其状态的节点。如图5所示,可以根据重点节点对交通网络进行划分。对单个子网中重点节点的状态转换,只需调整其子网内邻居节点的状态来解决。
交通网络可以如图5划分成若干组。一个或多个拥堵程度高(由PA预测)的节点作为一个组的中心,所有到中心的距离小于阈值D的节点划分为一个组。假设有 n个节点:J={j1,j2,…,jn},本文把交通流量按拥堵程度分成 k个级别:CS={c1,c2,…,ck}。MDP中的状态可以表示为st=lt;st1,st2,…, stngt;,其中,sti∈S 是节点 ji在 t时刻处于拥堵状态,si∈CS。策略πit={ait1,ait2,…,aitn},其中,动作aitk的作用是在t时刻引导一些车辆改变它们的路径(如可以通过导航软件提示等方法),从而减少k组的拥堵程度。本文假设在交通网络中分组时,任意 2组中心间的距离足够大,这意味着子动作间不存在依赖。因此上述分组的数据可以用分布式服务器处理,通过并行来提高系统性能。通过网络划分,把一个状态数为n的MDP转换成多个子MDP,每个子MDP的联合状态数远小于n,从而大大降低了问题规模。
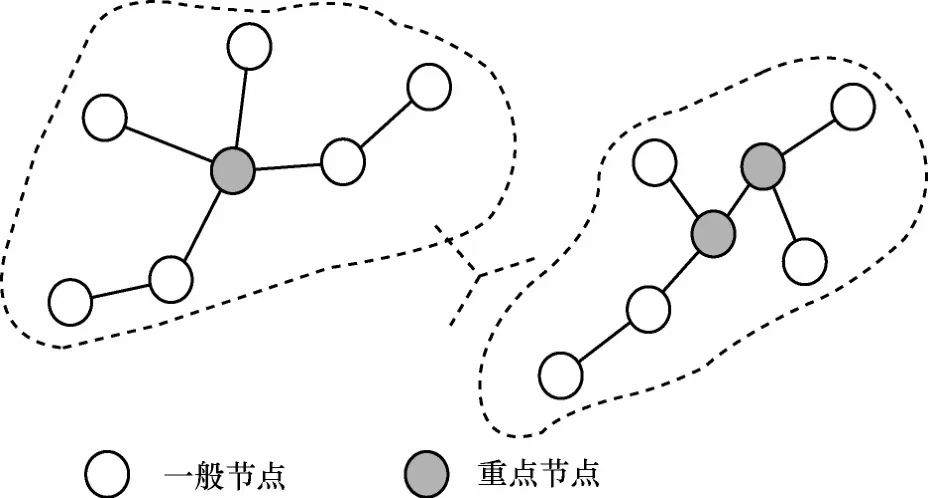
图5 基于重点节点的网络划分
算法2 并行调度方案
输入 已划分的交通网络分组V={v1,v2,…,vk},分布式系统中服务器节点C={c1,c2,…,cn}
输出 网络分组在处理节点中的分配方案
方法:

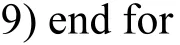
其中,分布式系统为同构体系结构,并且服务器节点数目n小于子网分组数k,vk.s是分组vk中所有节点拥堵程度总和。根据vk.s的值对V进行排序,放入堆 MaxHeap中。遍历 MaxHeap,通过Assign(cn,vk)将当前分组任务分配给 cost最小的服务器,随后对服务器的cost值进行修正。此算法实现了分布式服务器的负载均衡,相对于单节点,处理性能会有大幅度的提高。
根据观察结果,在前述MDP模型中加入新的变量G,代表子状态节点的网络结构。G=(V,E),其中,V为节点的集合,E为边的集合。一个边(i,j)存在表示节点i影响节点j的状态。
定义4 邻居状态节点。对于任意状态节点i∈V,其邻居状态节点N(i)={j∈V |di,j≤k},其中,di,j为i和j之间的路径长度,k是阈值。定义4表明一个节点的状态只受邻居节点状态的影响。
通过定义邻居节点,和重点节点相关的联合状态数进一步缩小,从而进一步降低问题的规模。
定义5 状态转换分解。设有n个状态的子节点,对应的动作也分为n个子动作,则根据前面的观察结果,有

其中,s表示当前状态,s'表示下一个状态。
定义6 报酬分解。设有n个状态的子节点,对应的动作也分为n个子动作,则根据前面的假设,有

定义6意味着整体报酬被分解为若干个组的报酬。每一组的报酬又进一步分解为所有邻居节点的报酬。这样每个节点的报酬可以采用单机多处理器的并行方式来计算。
在交通CPS中,当一个动作ai被执行,节点i处的交通流量为
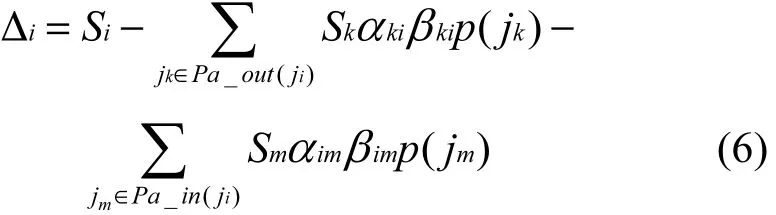
其中,Pa_out(ji)是尝试减少节点i处流量的节点集,Pa_in(ji)是尝试增加节点 i处流量的节点集,αki是Sk流向节点i的比例。假设并不是所有车辆都会按本文的策略来改变行驶路线,那么 βki是 Sk受动作ai影响的比例,P(jk)是在节点k处的车辆根据ai改变路线的概率,它可以从历史数据得到。整体的状态事务概率可以用P(j)和∆i计算。
根据定义 6,可以定义平均流量和其中一组gi的方差为
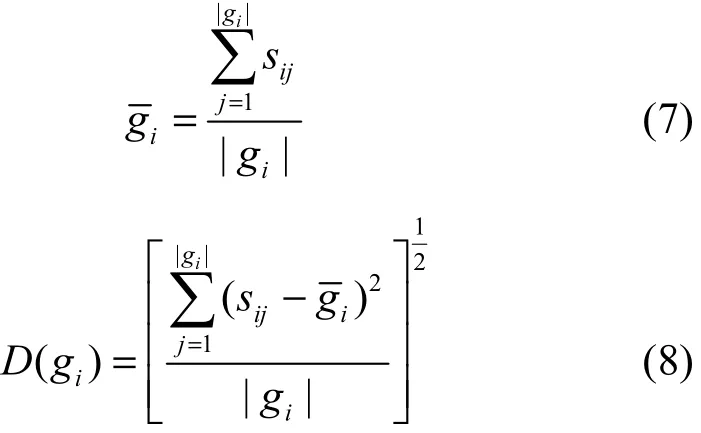
本文的目标是把所有拥堵状态最小化。因此,定义欧式距离子动作的报酬函数和整体报酬函数为
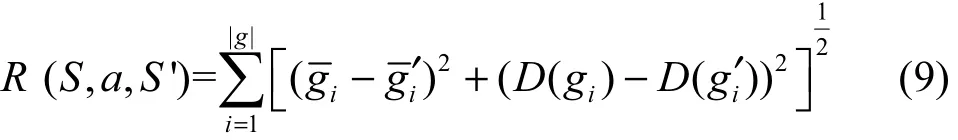
最终,最优策略可以按式(10)计算。
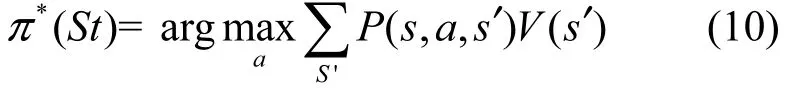
5 实验结果与分析
SUMO是一个开源的微观道路交通仿真模拟器[22],它可以检测通过相应区域车辆的数量和每辆车的位置。如图6所示,本文用JADE(Java agent development framework)框架对 SUMO进行扩展来支持多agent系统,同时使用 SUMO的TraCI接口来获得感应圈变量和车辆位置的变量,用它们来模拟RFID和GPS阅读器。基于这个框架,agent控制器用智能算法控制车辆在 SUMO中移动,从中获取事件数据和执行相应的动作。在实验中,在地图里设置了80个路口和8万辆汽车。为了更接近真实的交通系统,定义了一组规则:每辆车都有一个家的位置和办公室位置,车辆Vi在家和办公室之间运行的概率是 pi。这些车辆还有相应概率去超市、医院等其他地点。此实验模型可以满足 PCEP对交通网络的划分、状态和动作的分解等操作,并且可以并行的生成决策方法。本文把4台至强E3处理器和16 GB内存的服务器当作数据处理服务器。另一台有4 GB内存的PC运行SUMO。

图6 系统实现框架
首先来评估ISCEP关于多查询的处理性能。本文对经典的RCEDA方法[23]进行了类似本文提出的概率计算方式的拓展,称之为 PRCEDA(probability RCEDA)。通过PRCEDA与本文提出的ISCEP进行比较。假定所有的注册查询都是二叉树且Query Depth不超过4层,从图7中可以观察到,随着注册查询数目的加大,ISCEP的时间消耗增长幅度相比 PRECDA要小很多。因为PRECDA以轮询方式查询匹配树,随着注册查询数目的增加,查询效率会越来越低。使用查询映射表的ISCEP轮询次数要少很多,所以查询效率下降较少。

图7 查询处理性能
下一个实验评估该系统的平均拥堵度,结果如图8所示。本文把拥堵程度划分为11个等级,其中,“0”表示无拥堵,“10”表示拥堵程度最高。从图中可以观察到使用本文方法比让汽车自主行驶时平均拥堵度明显降低。原因是本文方法发现节点可能出现拥堵时,会主动引导后续车辆向轻负荷节点行驶。同时,当车辆总体拥堵程度比较高的时候,本文方法带来的拥堵下降也更多。原因是当总体车流量比较大时,系统执行的动作会影响更多的车辆,带来更多的拥堵下降。

图8 拥堵程度比较
最后的实验中采用不同数量的服务器和不同大小的数据来测试本文方法的性能。重点节点的数量固定在20,其结果如图9所示。结果表明,本文方法通过网络的划分、邻居节点定义及状态和动作分解,可以在较大规模的MDP问题中在可接受的时间内形成决策。从图中可以看到,生成决策的平均消耗时间随着车辆数量的增加成正比。原因在于车辆数量的增加需要执行更多的子动作,因此增加了算法的复杂性。通过本文方法还可以发现随着车辆数量的增加,4个服务器的性能更好,而且生成决策所需的时间增长相对较慢。这说明系统具备更好的可扩展性,在一定范围内可以通过增加新的计算资源来支持更大规模的交通网络。
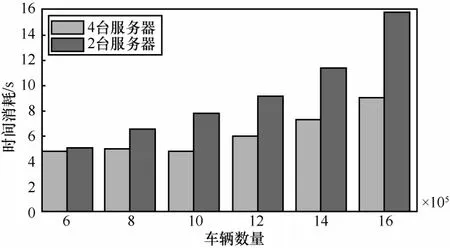
图9 不同服务器数量的性能
6 结束语
本文提出了一种对 CPS设备产生的不确定性事件流进行处理分析,然后在基于ADBN的预测结果上引入并行MDP模型来控制大规模交通拥堵的主动式复杂事件处理方法。实验评估表明,该方法能够有效地减少节点的拥堵程度,并且具有良好的可扩展性。但在并行MDP中,子状态和子响应的空间随着节点和车辆的增加依然会变得巨大。今后的工作重点在于研究如何进一步减少子状态的空间数量,从而提高系统的整体性能。
[1] LUCKHAM D C. The power of events: an introduction to complex event processing in distributed enterprise systems[M]. Boston, Addison Wesley, 2002.
[2] ENGEL Y, ETZION O. Towards proactive event-driven computing[C]//The Fifth ACM International Conference on Distributed Event-Based Systems. 2011: 125-136.
[3] ETZION O, NIBLETT P. Event processing in action[M]. Manning Publications, 2010.
[4] WU E, DIAO Y, RIZVI S. High-performance complex event processing over streams[C]//2006 ACM SIGMOD International Conference on Management of Data. 2006: 27-29.
[5] AGRAWAL J, DIAO Y, GYLLSTROM D. Efficient pattern matching over event streams[C]//SIGMOD Conference. 2008: 147-160.
[6] ZHANG H, DIAO Y, IMMERMAN N. Recognizing patterns in streams with imprecise timestamps[J]. PVLDB, 2010, 3(1): 244-255.
[7] XU C, LIN S, LEI W. Complex event detection in probabilistic stream[C]//The 12th International Asia-Pacific Web Conference. 2010:361-363.
[8] KAWASHIMA H, KITAGAWA H, LI X. Complex event processing over uncertain data streams[C]//The Fifth International Conference on P2P, Parallel, Grid, Cloud and Internet Computing. 2010: 521-526.
[9] KAWASHIMA H, KITAGAWA H, LI X. Complex event processing over uncertain data streams[C]//3PGCIC. 2010: 521-526.
[10] WELBOURNE E, KHOUSSAINOVA N, LETCHNER J, et a1. Cascadia: a system for specifying, detecting, and managing RFID events[C]//The 6th International Conference on Mobile Systems, Applications, and Services. 2008: 281-294.
[11] DOLEV S, KOPEETSKY M, SHAMIR A. RFID authentication efficient proactive information security within computational security[J].Theory of Computing Systems, 2011, 48(1):132-149.
[12] KUNZ T, ALHALIMI R. Energy-efficient proactive routing in MANET: energy metrics accuracy[J]. Ad Hoc Networks, 2010, 8(7):755-766.
[13] ENGEL Y, ETZION O, FELDMAN Z. A basic model for proactive event-driven computing[C]//The 6th ACM International Conference on Distributed Event-Based Systems (DEBS'12). 2012: 107-118.
[14] ENGEL Y, ETZION O. Towards proactive event-driven computing[C]//The Fifth ACM International Conference on Distributed Event- Based Systems, DEBS. 2011: 125-136.
[15] JIA Q S. On state aggregation to approximate complex value functions in large-scale Markov decision processes[J]. IEEE Transactions on Automatic Control, 2011, 56(2):333-344.
[16] SUN T, ZHAO Q C, LUH P B. Incremental value iteration for time aggregated Markov decision processes[J]. IEEE Transactions on Automatic Control, 2007, 52(11):2177-2182.
[17] POWELL W B. Approximate dynamic programming: solving the curse of dimensionality[M]. New York, Wiley-Inter Science, 2007.
[18] JIA Q S, ZHAO Q C. Strategy optimization for controlled Markov process with descriptive complexity constraint[J]. Science in China,2009, 52(11):1993-2005.
[19] WANG Y H, CAO K N, ZHANG X M. Complex event processing over distributed probabilistic event streams computers and mathematics with applications[J]. Computers amp; Mathematics with Applications,2012, 66(10): 1808-1821.
[20] PASCALE A, NICOLI M. Adaptive Bayesian network for traffic flow prediction[C]//Statistical Signal Processing Workshop (SSP). IEEE,2011: 177-180.
[21] 王永恒, 杨圣洪. 分布式 RFID数据流的复合事件检测方法[J]. 计算机应用研究, 2011, 28(11): 4177-4179.WANG Y H, YANG S H. Complex event detection method for distributed RFID systems[J]. Application Research of Computer, 2011,28(11): 4177-4179.
[22] BEHRISCH M, BIEKER L, ERDMANN J, et al. Sumo - simulation of urban mobility: an overview[C]//The Third International Conference on Advances in System Simulation. Barcelona, Spain, 2011: 63-68.
[23] WANG F, LIU S, LIU P, et al. Bridging physical and virtual worlds:complex event processing for RFID data streams[C]//The 10th International Conference on Extending Database Technology (EDBT'2006).2006: 588-607.
Research of proactive complex event processing method
GENG Shao-feng1,2, WANG Yong-heng1, LI Ren-fa1, ZHANG Jia2
(1. College of Information Science and Engineering, Hunan University, Changsha 410082, China;2. College of Computer Engineering, Jimei University, Xiamen 361021, China)
Based on the preliminary analysis results of the indeterminate event stream that generated by the sensors and control purpose equipment of CPS, the adaptive dynamic Bayesian network and parallel Markov decision process model were used to support the proactive complex event processing. In order to resolve the vast state space issue of Markov decision process for large CPS, states partition and reward decomposition methods were proposed to parallel the decision making process. The experimental result based on the simulation of traffic network shows that proposed method can process event stream effectively and has favorable scalability.
CPS, big data, complex event processing,Markov decision process
s: The National Natural Science Foundation of China(No.61173036, No.61371116), Foundation of Fujian Educational Committee (No.JA14186)
TP391
A
10.11959/j.issn.1000-436x.2016183
2016-04-07;
2016-06-26
国家自然科学基金资助项目(No.61173036,No.61371116);福建省教育厅基金资助项目(No.JA14186)

耿少峰(1981-),男,河南台前人,湖南大学博士生,主要研究方向为 CPS、复杂事件处理等。

王永恒(1973-),男,河北霸州人,湖南大学副教授,主要研究方向为物联网、数据挖掘等。

李仁发(1957-),男,湖南宜章人,湖南大学教授、博士生导师,主要研究方向为CPS、嵌入式系统和无线传感网等。
张佳(1980-),女,河南新乡人,集美大学讲师,主要研究方向为物联网、嵌入式系统等。

