基于DAA的轻量级多商家多重息票系统

柳欣，徐秋亮，张波

（1. 山东青年政治学院信息工程学院，山东 济南 250103；2. 山东省高校信息安全与智能控制重点实验室（山东青年政治学院），山东 济南 250103；3. 山东大学计算机科学与技术学院，山东 济南 250101；4. 济南大学信息科学与工程学院，山东 济南 250022）

基于DAA的轻量级多商家多重息票系统

柳欣1,2，徐秋亮3，张波4

（1. 山东青年政治学院信息工程学院，山东 济南 250103；2. 山东省高校信息安全与智能控制重点实验室（山东青年政治学院），山东 济南 250103；3. 山东大学计算机科学与技术学院，山东 济南 250101；4. 济南大学信息科学与工程学院，山东 济南 250022）

基于Brickell等的DAA（direct anonymous attestation）方案提出一个支持多商家环境的多重息票系统。新系统将多重息票中的关键元素与抗篡改的TPM（trusted platform module）芯片进行绑定，从而能更有效地阻止用户的共享行为。新系统的构造过程使用了Chow等的服务器辅助签名验证技术、Yang等的自盲化证书技术以及Peng等的区间证明技术，使用户在息票发布和兑换协议中均无需执行低效的对运算。相对于多个同类系统，新系统同时满足多个较理想的性质，而且与ARM TrustZone平台上的移动支付框架兼容。此外，新系统在通信和运算耗费方面具有明显优势。

多重息票；直接匿名证明；服务器辅助签名验证；区间证明；不可分割性

1 引言

息票（coupon）是一种传统的广告和促销手段。目前，电子息票（e-coupon）已在电子商务领域得到广泛应用，且能有效解决传统纸质息票的环境污染问题[1]。此外，还提出了移动息票[2]（m-coupon）和多重息票[3～9]（MC, multi-coupon）的概念。其中，MC可视为包含k张可独立兑换息票的集合，它有助于商家与客户建立长期的购买关系，形成稳定的购买群体。出于安全性的考虑，多重息票系统（MCS,multi-coupon system）必须满足以下性质。为了保护商家利益，不允许顾客使用伪造的MC进行兑换，也不允许多名顾客对同一张MC进行分割使用。同时，为了保护顾客的隐私，应当确保顾客交易过程的机密性和同一名顾客的多个交易间的无关联性。

2005年，Chen等[3]提出MCS的安全模型，同时设计了一个实例化的系统。然而，该系统的最大缺点是息票发布和兑换阶段的复杂度线性依赖于MC的价值。此后，文献[4]提出了通信和运算复杂度均独立于MC价值的改进系统。但是，该系统的弱点是要求将k作为系统的固定参数。2007年，Chen等[5]指出已有系统[3,4]仅满足弱不可分割性（weak unsplittability），即只要客户 U1、U2间存在完全信任关系，就可以通过复制操作实现对MC的分割使用。为此，Chen等构造了满足强不可分割性（strong unsplittability）的改进系统，即只要客户U1、U2相互信任且U1承诺在共享使用MC后与U2执行某种交互，就能确保U2可以继续使用MC。由于要求顾客以固定顺序进行兑换，因此 Chen等的系统仍无法满足实际应用的需要。文献[6]指出，已有的MCS仅考虑了单一商家的情况。为了实现客户友好性质，应当将此类系统推广至更具有一般性的环境，即允许不同类型的商家构成联合体，当获得由任何一个商家颁发的MC之后，顾客可以向联合体中的其他商家进行兑换。为此，文献[6]提出第一个支持多商家环境的MCS，且无需限制兑换顺序。需要指出的是，文献[6]系统的缺点是联合体的公/私钥对是在商家间共享的，一旦某个商家退出联合体，将为 MCS带来安全隐患。此外，联合体是以静态方式创建的，并未考虑商家的动态加入问题。最近，文献[7,8]提出多个满足额外性质的改进系统，如支持批量兑换、息票发布子协议满足并发安全性等。但是，这些系统[7,8]并不支持多商家环境。2015年，Hinarejos等[9]提出一个轻量级的多商家多重息票系统。然而，该系统的用户匿名性是借助群签名技术实现的，因此仅实现了较低的匿名性等级，即使客户保持诚实，也必须期望MC的发布者不与商家进行合谋。尽管采用群签名技术有利于通过揭示身份而实现对恶意用户的惩罚，但是最新的隐私增强匿名认证技术提倡采取“拒绝为欺诈用户提供服务而非损害其隐私”的宽容做法[10,11]。此外，该系统仅满足弱不可分割性。在文献[12]中，Canard等指出MC可用于为病人开具药物处方，并提出允许用户分割使用MC的系统。本文认为，文献[12]系统与上述系统[3～9]的应用目标并不一致。

从实际角度考虑，MCS应当同时满足以下性质：1)支持多商家应用环境，从而拓宽MC的使用范围，提高其兑换率；2)支持息票对象[5,6]的概念，即利用息票对象表示息票代表的商品或服务，因为不同商家提供的兑换服务是不同的；3)为顾客提供一定的灵活性，即允许顾客与发布者共同协商MC的价值以及商品类型；4)满足更强的不可分割性，因为已有系统[3～9]的不可分割性都是基于纯软件技术实现的，这种方式仅能为用户的共享行为设置障碍，而无法真正地阻止这种行为；5)系统的执行过程应当尽量避免用户执行低效的密码运算。已有系统[3～9]要求顾客执行RSA群上的模指数运算或者对运算。然而，这2类运算并不适合于移动设备[13～15]。

直接匿名证明（DAA, direct anonymous attestation）[16～19]是一类由可信计算组织（TCG, trusted computing group）提出的匿名证书系统，且适用于配置了专用安全芯片TPM（trusted platform module）的计算平台。DAA方案最初用于解决可信计算平台远程身份证明中的隐私保护问题[20]。当前，此类方案在众多应用系统的设计中同样得到广泛采用[19]。需要指出的是，标准的匿名证书系统（如文献[21]）往往难以杜绝用户复制和共享证书的行为。为此，Cesena等[18]利用DAA技术构造了可以阻止此类行为的匿名认证方案。

本文基于 Brickell DAA方案[16]提出一个改进的MCS。该系统具有以下的显著特点：1)商家间无需共享秘密信息，当某个商家离开联合体时，不会带来安全性问题；2)用户在息票发布和息票兑换协议中均无需执行对运算，因此本文 MCS在某种程度上是“轻量级的”；3)本文系统在新定义的多商家MCS模型下满足可证安全；4)在效率方面，本文系统的通信和运算耗费较已有系统有明显优势；5)本文MCS与Pirker等[22]的基于ARM TrustZone技术的移动支付框架相兼容，因为TPM端与Host端分别对应于 TrustZone系统的 Secure World环境和Normal World环境。

2 多商家多重息票系统的定义及安全模型

2.1 多商家多重息票系统的定义

本文MCS定义是在文献[9]定义基础上修改得到的。具体地，多商家环境下的 MCS可视为由以下算法/协议构成的集合，即Setup、Affiliation、Disaffiliation、Issue、Redeem和Claim。其中，Setup算法用于产生系统参数以及为发布者I产生公/私钥对。商家V通过与I执行Affiliation算法加入到联合体Fed中，且可以在今后通过与I执行Disaffiliation算法离开联合体。用户U利用Issue协议向发布者I申请MC，且MC中的每张息票都是可以独立兑换的。当希望获得某类商品或服务时，U通过执行Redeem协议向联合体Fed中的某个商家V兑换MC中的一张息票。此后，V通过Claim协议向I证明自己为U提供了兑换服务，从而要求后者向自己支付费用。在本文模型下，安全的 MCS应当满足如下安全性质。

1) 正确性：若诚实的用户U与发布者I执行Issue协议，并且获得由I提供的MC，则U总是能利用MC中未曾使用的息票向联合体Fed中的商家V兑换商品或服务，且V总是能向I证明这个事实，使后者向自己支付相应的费用。

2) 不可伪造性：由恶意用户构成的联合与诚实商家V执行的兑换次数不能超过他们通过执行Issue协议而取得的合法息票数量之和。同时，由恶意商家构成的联合无法向I做出虚假声明，即声明的兑换次数超过他们实际为诚实用户提供兑换服务的次数。

3) 无关联性：好奇的商家V无法对用户U执行Issue协议和Redeem协议的行为进行关联，也无法对该用户2次执行Redeem协议的行为进行关联。

4) 可声明性：若诚实的商家V为用户U兑换了某张息票，则他总是能向I证明这个事实。

5) 不可分割性：用户U1无法与另一个用户U2分割使用自己的MC。

2.2 多商家多重息票系统的安全模型

在文献[9]中，Hinarejos等提出一个MCS安全模型。但是，Hinarejos等[9]要求的防止息票重复兑换性质完全可以由不可伪造性所蕴含。此外，Hinarejos等将无关联性实验分为2个模式，即分别在“由恶意商家构成联合”与“由恶意商家和发布者构成联合”2种情况下进行分析。本文认为无需再对这2种情况进行细分，因为若MCS在后一种情况下满足无关联性，则在前一种情况下同样满足无关联性。为此，本文结合文献[6,9]的安全模型定义提出更为简洁的 MCS安全模型。在本节的描述中，符号Adv与B分别表示安全性实验中的攻击者与归约算法，U、V、I分别表示诚实用户、商家以及发布者，分别表示恶意（或被攻破的）用户、商家以及发布者，表示部分被攻破的用户，即的host部分已经被攻破，但TPM部分仍然保持诚实。表1对Adv与B在不同安全性质实验中充当的角色进行了总结。

表1 Adv与B在不同安全性质实验中充当的角色

2.2.1 不可伪造性实验

该实验的执行过程分为以下2个模式。

1) 模式1

② 交互：B为Adv提供以下的预言服务。

散列询问：当Adv提出关于散列函数Hi的询问M，B向Adv返回。

Issue询问：当Adv请求获得一张MC，则B以I的身份与Adv执行Issue协议。

Semi-Issue询问：当Adv请求获得一张 MC，则B以部分被攻破用户的 TPM 的身份与Adv联合执行同I的Issue协议。

Redeem询问：当Adv请求向V兑换一张对象为ob的息票，则B以V的身份与Adv执行Redeem协议。

Semi-Redeem询问：当Adv请求向V兑换一张对象为ob的息票，则B以部分被攻破用户的 TPM的身份与Adv联合执行同V的Redeem协议。

Corrupt询问：当Adv请求攻破U，则B向Adv返回U的私钥，同时将U标记为被攻破的用户。

③ 结束：Adv输出ob*。若同时满足以下条件，则判定Adv在实验中获胜，即Adv向B兑换的“具有息票对象ob*”的息票数量大于它通过与B执行Issue协议而获得的“具有息票对象ob*”的息票数量。

2) 模式2

① 初始化：B执行模式 1中描述的初始化操作。此外，B定义计数器CtrR，用于统计已经为诚实用户执行的兑换次数。

② 交互：B为Adv提供以下的预言服务。

散列询问：描述方式同模式1。

Issue询问：当Adv请求为U发布一张MC，则B以I的身份与U执行Issue协议。

Redeem询问：当Adv请求为U兑换一张对象为ob的息票，则B以U的身份与Adv执行Redeem协议。

③ 结束：最终，Adv输出由Redeem协议副本构成的列表Ltrans，并且请求I为Ltrans中所含的交易支付费用，B以I的身份与Adv执行Claim协议。若Claim协议执行成功且满足则判定Adv在实验中获胜。

2.2.2 无关联性实验

该实验的具体过程分为以下阶段。

1) 初始化：B执行不可伪造性实验中描述初始化操作，并且向Adv提供

2) 交互：B为Adv提供以下的预言服务。

散列询问：描述过程同不可伪造性实验（模式 1）。

Issue询问：B以U的身份与Adv执行Issue协议，并且获得由Adv提供的MC。

Redeem询问：B以U的身份与Adv执行Redeem协议。

Corrupt询问：当Adv请求攻破U，则B将U标记为被攻破的用户。

4) 结束：Adv输出猜测结果b，若b=c，则判定Adv在实验中获胜。

2.2.3 可声明性实验

该实验的具体过程分为以下阶段。

1) 初始化：B执行无关联性实验中描述的初始化操作。

2) 交互：B为Adv提供以下的预言服务。散列询问：描述过程同不可伪造性实验。

Redeem询问：当Adv请求向V兑换一张对象为ob的息票，B以V的身份与Adv执行Redeem协议。

3) 结束：最终，Adv请求向V兑换一张对象为ob*的息票，若满足以下条件，则判定Adv在实验中获胜，即：①B与Adv成功执行Redeem协议并且获得对应的交易副本trans*；②当B以trans*为输入与Adv执行Claim协议时，该协议总是失败，即B无法证明自己为用户提供兑换服务这个事实。

2.2.4 不可分割性实验

该实验的具体过程分为以下阶段。

1) 初始化：B执行不可伪造性实验（模式1）中描述的初始化操作。

2) 交互：B为Adv提供以下的预言服务。

散列询问：描述过程同不可伪造性实验（模式 1）。

Issue询问：描述过程同不可伪造性实验（模式 1）。

Semi-Issue询问：描述过程同不可伪造性实验（模式1）。

Redeem询问：描述过程同不可伪造性实验（模式 1）。

Semi-Redeem询问：描述过程同不可伪造性实验（模式1）。

3) 结束：Adv输出MC*。若同时满足以下条件，则判定Adv在实验中获胜，即：①MC*是有效的；②MC*的剩余价值大于0；③当B以MC*为输入执行Redeem协议时，该协议总是失败，这表明Adv已经将MC*的剩余价值转移至其他的MC′，即实现了对MC*的分割使用。

3 预备知识

令G1、G2、GT分别为素数p阶循环群，满足。令ˆ表示双线性映射，使G1×。令表示素数p阶循环群，满足

3.1 复杂性假设

q-SDH（q-strong Diffie-Hellman）假设[23]：对于任何的PPT（probabilistic polynomial time）算法A，定义概率

y-DDHI（decisional Diffie-Hellman inversion）假设[12]。对于任何的PPT算法A，定义概率

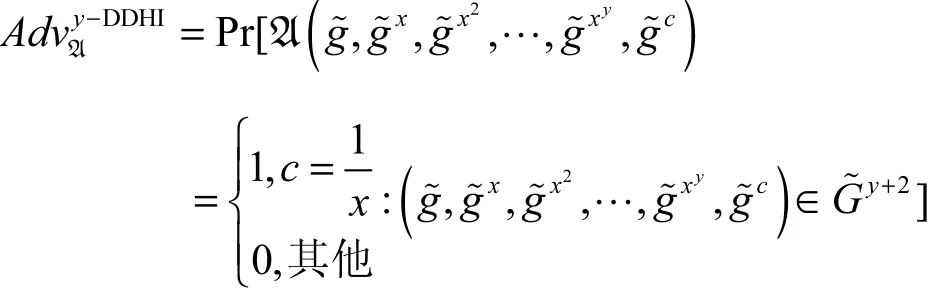
G1-DDH（G1- decisional Diffie-Hellman）假设[19]：对于任何的PPT算法A，定义概率

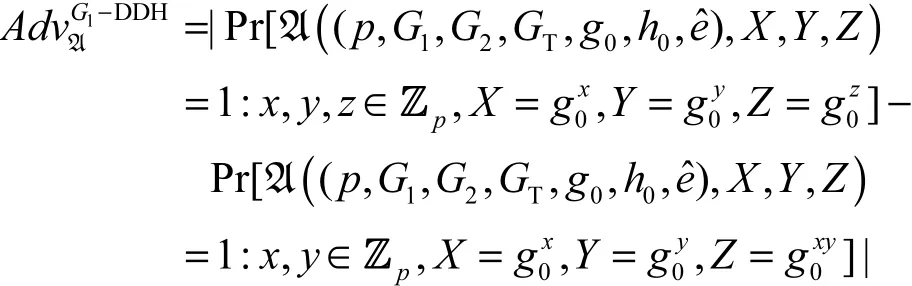
G1-DDH假设表明是可以忽略的。

3.2 BBS+签名方案

3.3 自盲化证书技术

最近，Yang等[24]提出了旨在减轻用户端运算耗费的自盲化证书技术。为了证明掌握 BBS+方案签名(A,e,s)，证明者选取f∈Zp，计算A′=Af,，其中，于是，证明掌握秘密元素，使验证等式成立，等价于证明掌握秘密元素使关系成立。此外，要求验证者额外验证等式是否成立以及是否满足

3.4 Peng-Yi区间证明技术

本文系统的构造过程要求使用 Peng等[25]的关于秘密元素j属于公开集合[1,Ji]的准确区间证明协议，记为。其基本思想是首先将目标证明等价为，其中。然后，计算秘密元素j−1关于底数的表达式，满足，从而将关于的证明约化为l个关于的更为简单的证明。现在，证明进一步等价于证明

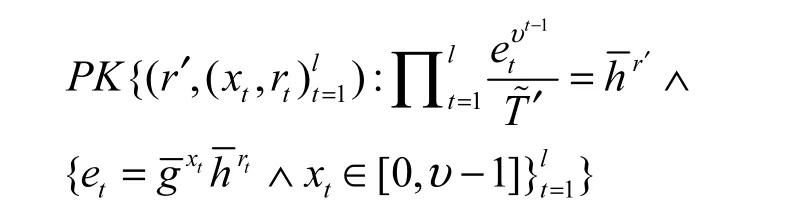
3.5 对委托运算协议与服务器辅助签名验证技术

委托运算技术有利于用户将繁重的运算任务委托给不可信的服务器，且此类运算模式特别适合于当前的云计算应用环境。对委托运算（pairing delegation）协议是一种委托计算技术，使用户端无需再执行昂贵的对运算。Canard等[15]指出，对委托运算协议应当满足完备性、可验证性和保密性。

服务器辅助签名验证（SASV, server-aided signature verification）技术的目标是帮助用户将数字签名验证过程中涉及的对运算任务委托给服务器。最近，Chow等[14]提出了一般性的SASV框架，且允许将任何对委托运算协议作为该框架的底层模块。此类技术要求满足以下性质：1)适应性选择消息与验证攻击下的存在的不可伪造性；2)合谋的适应性选择验证攻击下的可靠性。

4 对本文系统的描述

4.1 本文系统的设计思想

4.2 具体描述

4.2.1 系统中的参与方

在本文系统中，共涉及以下参与方，即由TPM和主机host构成的用户U，由多个商家构成的联合体

4.2.2 系统建立（Setup）

以安全参数1λ作为输入，I执行下列步骤。

6) 创建公共数据库DB，并且为DB创建任意的标准数字签名方案SIG下的公/私钥对，用于为向DB中写入重复检测标签的商家产生收据。创建废除列表BL，以及列表AL、ADL。

4.2.3 商家加入联合体（Affiliation）

希望加入Fed的商家V与I签署商业合作协议，其内容包括：规定V支持兑换的商品或服务类型，I承诺为V提供兑换服务而支付费用等。然后，I为V分配身份标识idV，执行AL←AL∪

4.2.4 息票发布（Issue）

该协议由U（host+TPM）和I共同执行。假设TPM 已经与I建立起可信信道[16]。为了提高在线运算效率，假设TPM已事先选取，并计算，具体步骤如下。

上述的cnt是TPM内部计数器。本文允许用户通过多次执行当前协议而获得多个MC，且假设在每次执行当前协议时，cnt的取值不变。

4)I验证nI。对于每个sk′∈BL，I验证是否满足若满足，则计算，验证是否满足。若不满足，则选取e, s∈RZp，计算向TPM发送

5) TPM向host发送(F1,mid,cre)，host验证cre是否为关于的有效 BBS+签名，即是否满足验证等式

为了提高验证效率，host利用 Chow 等[14]的SASV技术进行验证，具体过程如下。

4.2.5 息票兑换（Redeem）

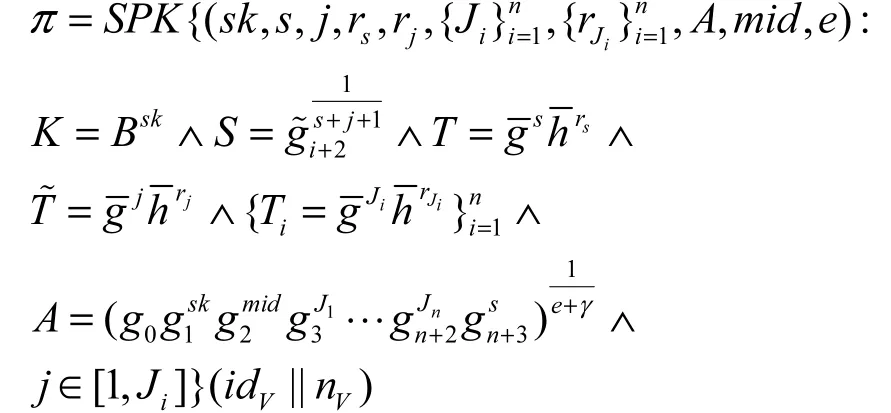
4) 若V接收到收据（receipt），则利用PKDB验证receipt的有效性，然后，V为用户提供所请求的类型obi的服务，并且保存交易副本。相反，若V接收到的是出错信息，则拒绝为U提供兑换服务。

4.2.6 声明（Claim）当V已经积累了由若干兑换交易副本构成的列表，且希望向I索取费用，则与I执行以下步骤。

2) I检查是否满足idV∈AL，若满足，则对于Ltrans中的每个交易副本，I执行如下检查：①验证知识签名π的有效性；②验证是否满足S∈DB；③验证receipt的有效性。若上述检查都通过，则I为V支付费用。相反，若满足S∉DB或receipt验证失败，则判定V进行欺诈。

4.2.7 商家退出联合体（Disaffiliation）

5 知识签名π的实现过程

为了便于理解，本文将π的执行过程分成2个子签名π1、π2进行描述。

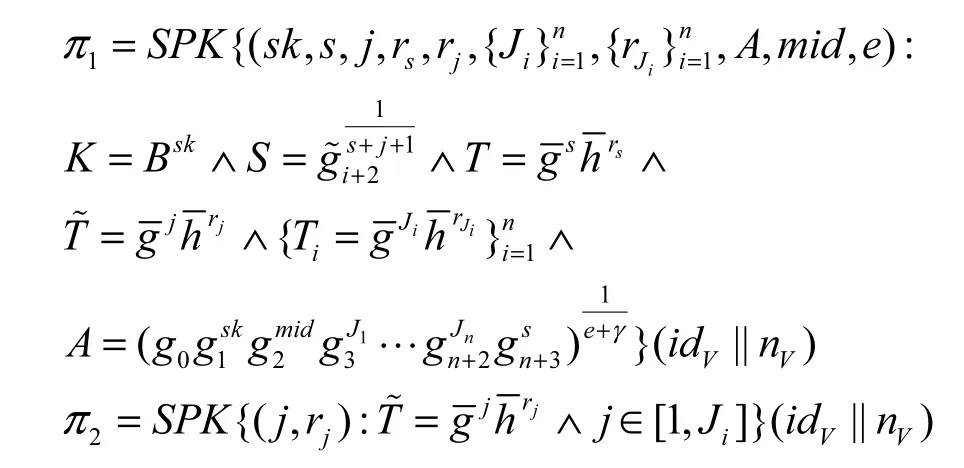
5.1 子签名π1的实现过程

在π1的构造过程中，本文采用Yang等[24]的自盲化证书技术对 Au等[23]的关于“掌握有效BBS+方案签名”的方法进行了优化。π1的最终形式为

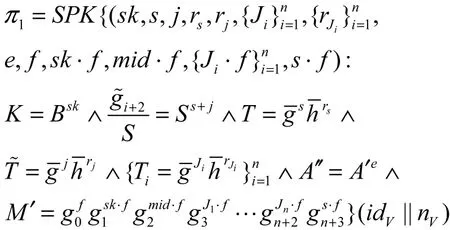
π1的具体产生过程如下。

2) host在[1,Ji]中选取未使用过的序号j，计算重复检测标签，选取 rs∈RZp，计算，选取，计算。对于，选取，计算

5) host在Zp上计算

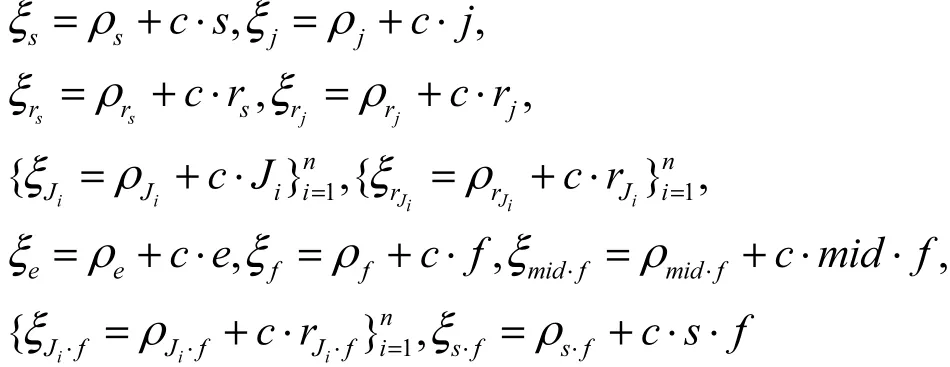
π1的验证过程如下。

5.2 子签名π2的实现过程

根据3.4节可知，可以利用Peng等[25]的小区间准确区间证明技术将转换为

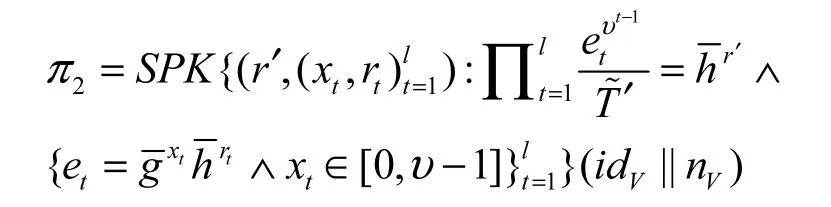
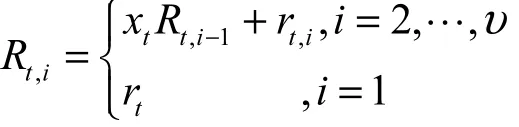
3) 将π2细化为如下形式

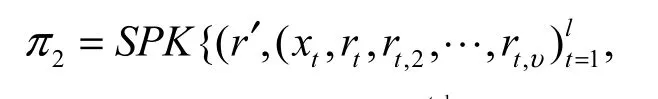
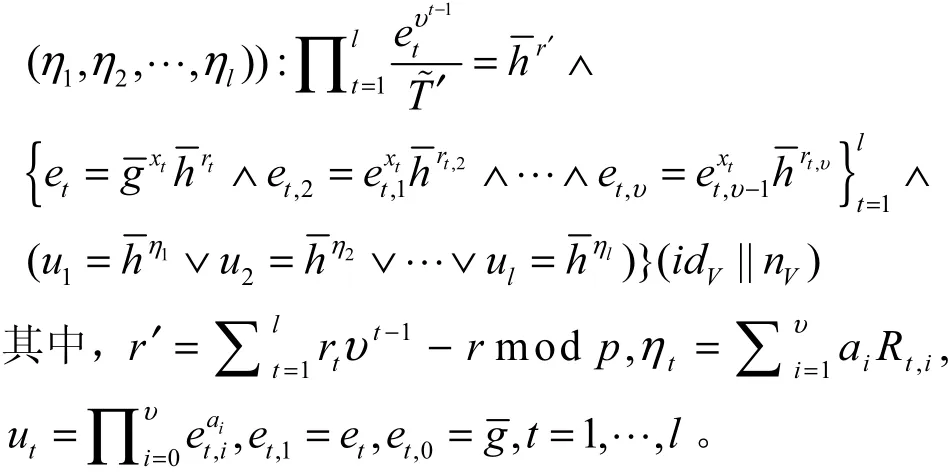
π2的验证过程如下。

2)采用π2产生过程中的方式计算系数，计算。计算验证是否满足

5.3 子签名π1与π2的合成

知识签名π是通过对子签名π1、π2执行并行合成而得到的。最终的合成结果为

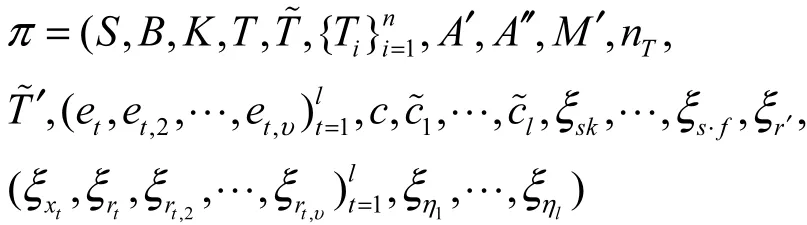
在验证过程中，验证者需要根据5.1节和5.2节的方式计算且最终的验证等式为

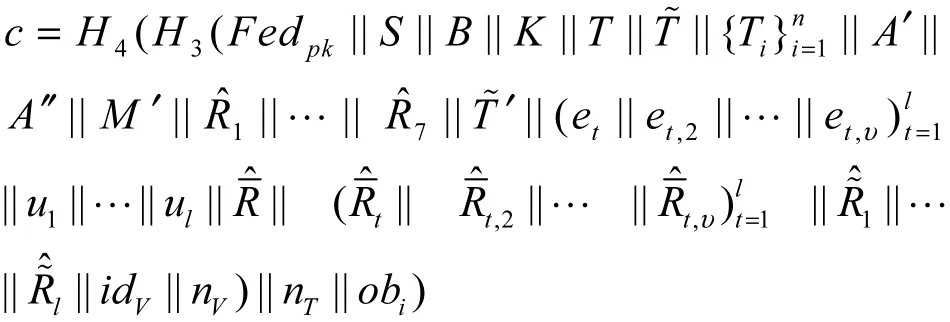
6 安全性分析

证明 限于篇幅，省略了正确性的证明过程。

1) 不可伪造性。当前实验分为以下2个模式。

散列询问：根据文献[16]的结论，无需将散列函数H1、H3视为随机预言机，因为它们都是内部函数。因此，B只需提供对函数H2、H4的模拟，即对于Adv提出的询问，B返回在Zp上随机选取的元素作为应答，同时确保所提供的应答满足一致性。

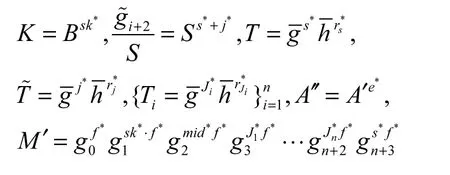
显然

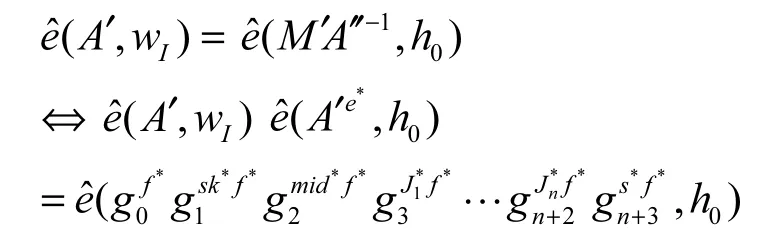
Corrupt询问：当Adv请求攻破用户Ui，若Ui在Reg的对应表目中的标识位满足c=0，则B向Adv返回Ui的私钥ski，设置Adv在当前实验中获胜的条件是，使。根据底层区间证明协议[25]的可靠性以及伪随机函数[26]的抗碰撞性，Adv不可能实现对MC的透支使用，也不可能利用使用过的重复检测标签S执行兑换而不被发觉。因此，若Adv在实验中获胜，则它必然在某次兑换过程中成功实现了对BBS+签名方案实例的伪造攻击。于是，B可以利用上述的重绕技术提取出关于秘密元组(sk**,的 BBS+方案签名Reg且sk**∉BL，即违背了q-SDH假设。

② 模式2。B执行当前实验模式2下的初始化操作，并且定义计数器CtrR。在当前实验中，B为Adv提供以下的预言服务。

散列询问：描述方式同模式1。

Issue询问：当Adv请求为U发布一张MC，则B自行模拟I与U执行Issue协议的过程。

Redeem询问：当Adv要求为用户U兑换一张对象为obi的息票，B以U的身份与Adv执行Redeem协议。若该协议执行成功，则B设置

最终，Adv输出由Redeem协议副本构成的列表Ltrans，若Ltrans中的每个副本都能通过Claim协议的验证过程且满足则表明，且该副本并非通过与B执行Redeem协议而获得的。此时，B对Adv执行重绕，必然能从π*中提取出关于秘密元组的 BBS+方案签名即违背了q-SDH假设。

散列询问：描述过程同不可伪造性实验（模式1）。

情况 1：若满足i=i*，B设置 F1=v且自己并不掌握B采用以下方式模拟Issue协议，即选取，选取，计算，设置

无论属于哪种情况，当Issue协议结束后，B均需执行以下操作。

④若i=i*，则设置，其中，符号“*”表示未知元素。否则，设置

情况1：若满足i=i*，则B采用模拟方式产生知识签名π。

情况2：若i≠i*，则B以诚实方式产生知识签名π。

Corrupt询问：当Adv请求攻破用户Ui，若，则B运行失败；否则，B采用不可伪造性实验（模式1）中的方式模拟当前询问。

①B以Uc的身份与执行Redeem协议，并且在该协议中向兑换第α0张MC中的第β0张息票。在该协议中，B选取r∈RZp，设置且采用当前实验Redeem询问中的技术模拟产生知识签名π。

②B以U1−c的身份与执行Redeem协议，并且在该协议中向兑换第α1张MC中的第β1张息票。在该协议中，B以诚实方式产生知识签名π。

最终，Adv输出对挑战比特c的猜测结果b。若满足b=c，则B判定z为群G1上的随机元素，否则，B判定z=uab成立，从而攻破了群G1上的DDH假设。

注意，Adv同样无法在当前实验中借助U0, U1在兑换过程中产生的重复检测标签S对它们进行分辨。因为，根据文献[13]结论，在群上的y-DDHI假设下，元素S与上的随机元素是不可分辨的。

3) 可声明性。B执行可声明性实验的初始化操作，并且采用可声明性实验中定义的方式回答Adv提出的散列询问和Redeem询问。由于Claim算法中的验证操作是V在Redeem协议中执行的验证操作的子集，因此，Adv将无法在该实验中获胜。

4) 不可分割性。B执行不可分割性实验的初始化操作。此外，B创建计数器，该计数器的取值代表了第i张MC的剩余价值，其中N表示Adv提出的Issue询问次数上界。B创建一维数组，其中，用于存储为Adv发布的第i张MC。在实验中，B为Adv提供以下的预言服务。

散列询问：描述过程同不可伪造性实验（模式1）。

Issue询问：假设B已经为Adv发布了i−1张MC。当Adv提出询问B利用重绕技术提取出秘密知识B为Adv产生crei=。B 设置

Semi-Issue询问：假设B已经为Adv发布了i− 1张MC。当Adv提出询问(J1,?,Jn)，B自行选取，为Adv产生。B设置

Redeem询问：B以V的身份与Adv执行Redeem协议，并且通过对Adv执行重绕而提取出秘密知识。B根据mid在数组中进行查找而判定Adv使用的是哪张MC。假设满足B设置

Semi-Redeem询问：B的模拟过程同不可伪造性实验（模式1）。

最终，Adv输出某张MC*的序列号mid*，满足，B根据计数器的取值而判定的剩余价值是否大于零。若是，则B以为输入执行Redeem协议。显然，该协议总是能执行成功。由于用户因满足而无法通过Redeem协议的验证过程，同时用户的host部分不掌握TPM私钥，因而无法实现对MC*的分割使用，即Adv将无法在当前实验中获胜。

尽管对委托运算协议[14,15]有利于减轻用户的运算负担，但是在现实应用中无法确保提供委托运算服务的服务器一定保持诚实。由于对Φ的调用发生在用户端host对证书进行验证的环节，因此，需要对定理 1证明过程中涉及“由归约算法B充当诚实用户且由攻击者Adv充当恶意参与方”的攻击场景进行重新讨论，即需要对不可伪造性实验（模式2）和无关联性实验进行重新讨论。同时，在本节假设Adv总是与提供对运算服务的恶意服务器（记为）进行合谋。

引理 1 在不可伪造性实验（模式 2）中，即使攻击者Adv与恶意服务器进行合谋，也无助于它在该实验中获胜。

证明 除了定理1中描述的执行过程，当前实验还可以以下方式执行。B设置列表Lcre，用于保存以诚实方式产生的用户证书。在实验执行过程中，B为Adv提供以下的预言服务。

采用类似的技术，可以证明以下3个引理。

引理 2 在不可伪造性实验（模式 2）中，即使攻击者Adv与恶意服务器进行合谋，也无法使诚实用户接受错误的委托运算结果。

引理 3 在无关联性实验中，即使攻击者Adv与恶意服务器进行合谋，也无法使诚实用户在服务器辅助验证和标准验证2种模式下获得不一致的验证结果。

引理 4 在无关联性实验中，即使攻击者Adv与恶意服务器进行合谋，也无法实现对诚实用户进行分辨。

定理 2 只要底层 BBS+签名方案在适应性选择消息攻击下满足存在的不可伪造性，同时底层对委托运算协议Φ满足完备性、可验证性和保密性，则在引入底层协议Φ后，本文MCS仍然是安全的。

证明 在不可伪造性实验（模式 2）和无关联性实验中，归约算法B以诚实用户身份与Adv和恶意服务器的联合进行交互。尽管B在执行交互过程中需要将对运算的任务委托给，但引理1～引理4表明，委托运算过程并不会有助于Adv在这2个实验中获胜。综上得出，在引入底层对委托运算协议Φ后，本文MCS仍然是安全的。

7 本文系统的性能分析

表2为本文系统与已有系统的主要性质对比。在发布协议中，表2中的所有系统在本质上均要求用户与商家（或发布者）执行一次或多次盲签名协议。其中，文献[5,6]系统要求执行的盲签名轮次与MC的价值k呈线性关系，而其他系统仅需执行 1次盲签名发布协议。在表2中，本文系统、文献[7]的方案 2以及文献[9,12]系统均支持息票对象的概念，因而允许用户利用1张MC兑换多种类型的商品或服务，而其他的系统仅允许兑换一种类型的商品或服务。早期的系统[3,4]要求将MC的价值k作为系统的固定参数，因而影响了其实用性，此后的系统均支持用户与发布者（或商家）协商k的取值。需要指出的是，本文系统和文献[6,9]系统均考虑了多商家联合经营的模式，因此满足更好的客户友好性质。如前所述，文献[3～9]系统都是利用纯软件的方法来确保多重息票的不可分割性，本文系统则借助 TPM 芯片实现了最强的不可分割性。此外，文献[12]系统是目前唯一支持对多重息票进行分割使用的系统。在匿名性方面，文献[9]系统因构造过程使用了群签名技术而实现了最弱的匿名性。

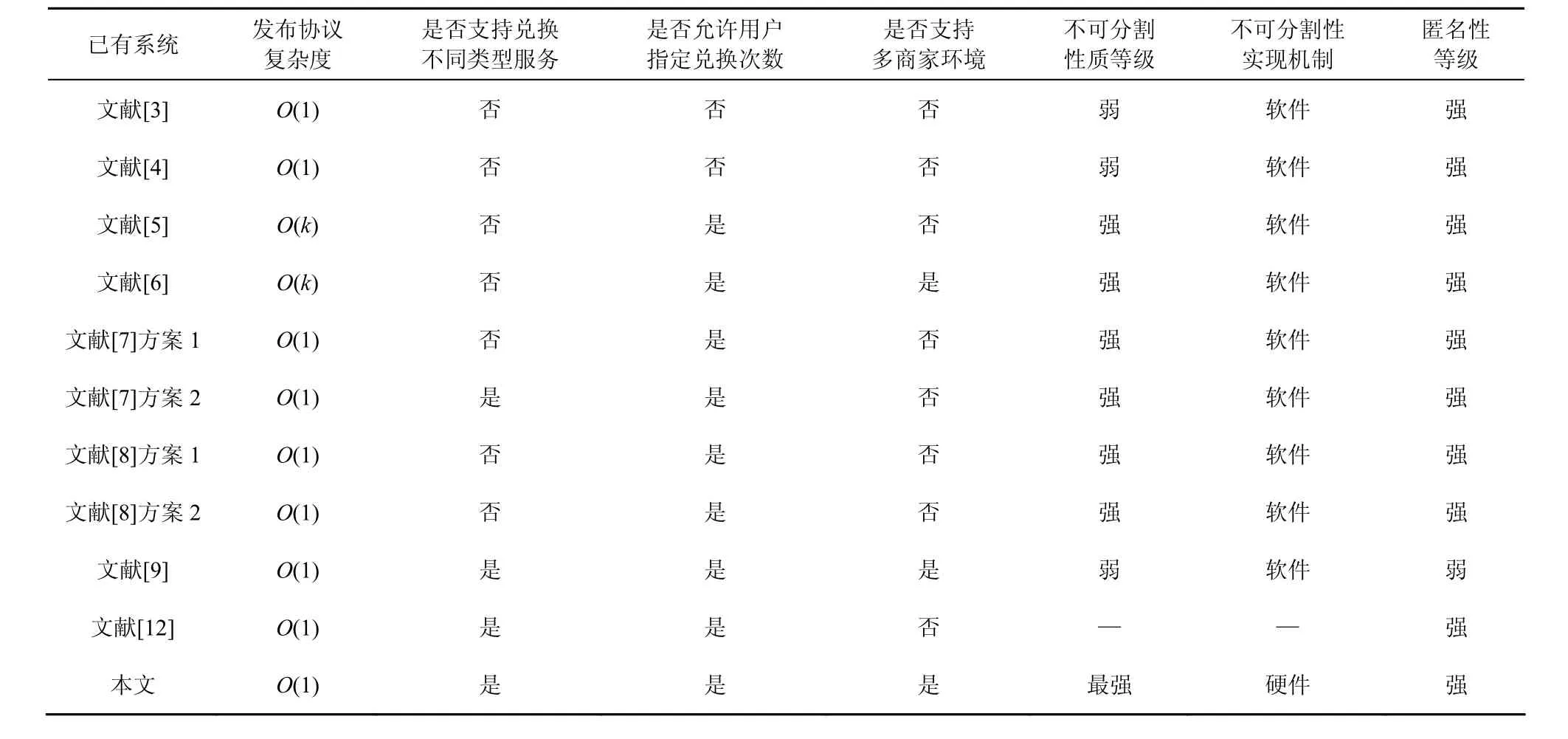
表2 本文系统与已有系统的主要性质比较

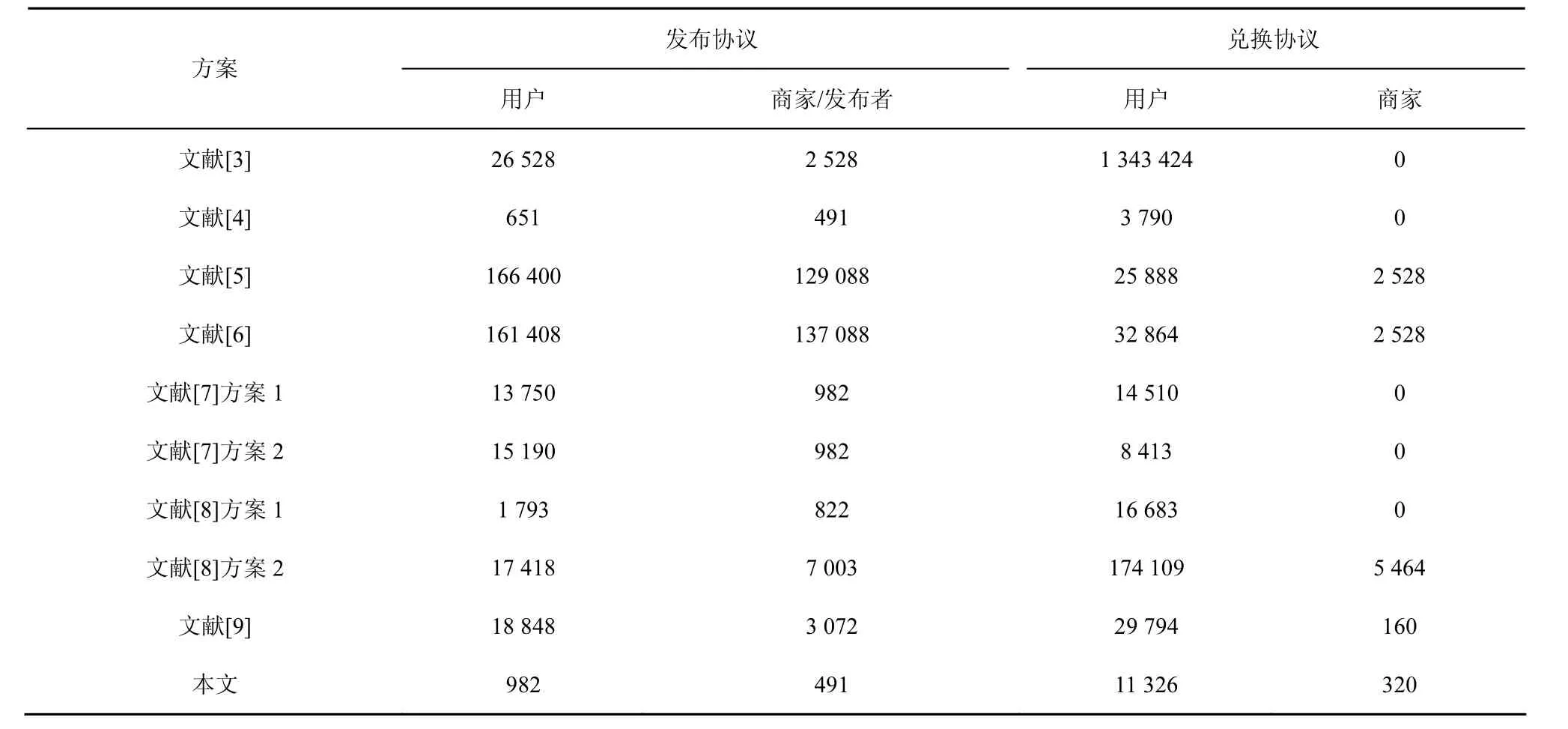
表3 本文系统与已有系统的通信耗费比较

表3和表4对本文系统与表2所列其他系统（文献[12]系统除外）进行了通信耗费和运算耗费的详细比较。所采用的具体方法如下。

1) 文献[3,5,6]系统都是在 RSA 群上构造的，本文选取了相同的安全参数[30]。文献[4]系统和本文系统都是在双线性群对12(G, G)上构造的，本文同样选取了相同的参数。此外，文献[7～9]系统的构造过程同时使用了RSA群与双线性群对。在比较中，本文用符号|G1|、|GT|分别表示群G1和目标群GT上的元素长度，表示有限域Zp上的元素长度，表示 RSA群上的元素长度。根据文献[24]的结论，当在MNT曲线上实现群对且以 80 bit安全性为目标时，满足

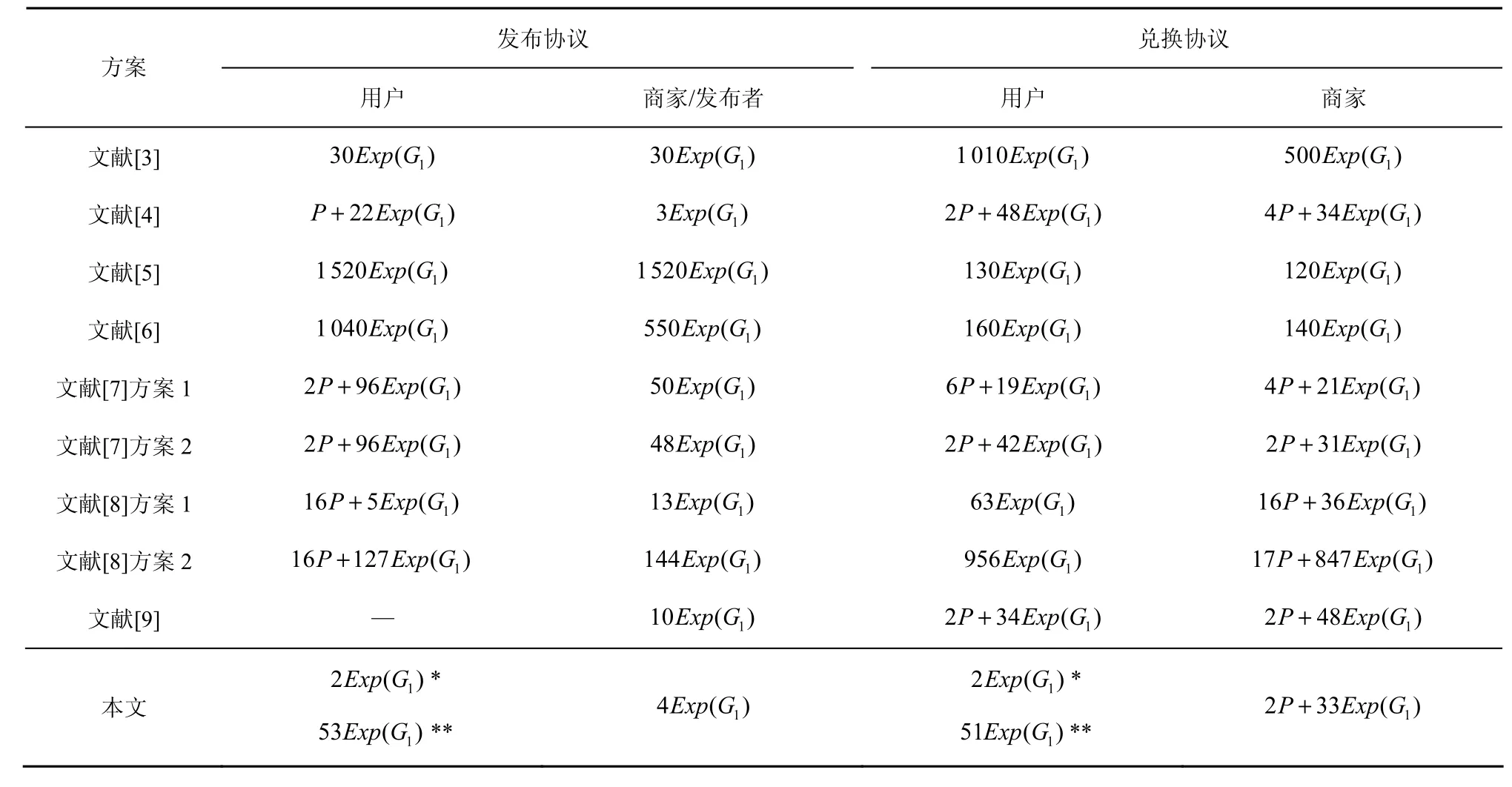
表4 本文系统与已有系统的运算耗费比较

2) 在运算耗费的分析中，本文并未对多指数运算与单指数运算进行区分，因为在对指数运算过程进行优化的情况下，这2种运算的耗费是接近的[24]。用符号P表示执行1次对运算的耗费，用和分别表示在群G1、G2、GT和Zn上执行1次指数运算的耗费。可以做出如下的估算，即此外，本文认为在文献[7]系统中，用户和商家需要执行群G1上指数长度为30 bit的小指数运算。根据“指数长度为x bit特的指数运算相当于1.5x次乘法”的结论[31]得出，1次群G1上的标准指数运算相当于 5次此类的小指数运算。最终，本文将G1、G2、GT和Zn上的指数运算以及小指数运算都估算为G1上的指数运算。

3) 在本文系统中，特定参数n表示MC支持兑换的服务类型种类，Ji表示第i类对象的数量。为了便于比较，本文假设用户在所有系统中仅申请一种类型的服务，于是n=1。同时，假设每张MC的价值均为50。不失一般性，对于本文系统，假设满足J1=50。此外，在本文系统的息票兑换协议中，底层的区间证明协议要求在以为底数的编码系统中对未使用过的息票序号进行分解。在文献[7]系统中，同样要求在u(ugt;2)进制下对MC的已兑换次数进行分解。此处选取

4) 在本文系统的息票发布协议中，用户需要调用底层的对委托运算协议实现对 BBS+方案签名的服务器辅助验证。为此，本文使用了文献[15]中的PVPV（public variable point and public variable point）类型协议。用户每次调用该协议的运算耗费约为

5) 在本文系统的Issue和Redeem协议中，发布者（或商家）还需要根据底层DAA方案的列表BL验证用户的 TPM 私钥是否因泄露而被废除，而参与比较的其他系统并未考虑这个问题。为了比较的公平，表4的运算耗费比较中并未统计执行此项检查的耗费。此外，用符号“*”和“**”对本文系统中TPM端和host端的运算耗费分别进行标记。

作为总结，本文系统实现了表2列举的所有重要性质。在通信耗费方面，本文系统仅次于最高效的文献[4]系统。在发布协议的运算耗费方面，本文系统接近于高效的文献[3,9]系统，且本文系统在兑换协议用户端的运算耗费方面是最高效的。

8 结束语

针对已有多重息票系统未能较好解决防止恶意用户对多重息票进行分割使用的现实问题，本文提出了基于DAA的轻量级多商家多重息票系统。相对于已有系统，本文系统不仅实现了支持兑换不同类型的服务、允许用户与发布者协商兑换次数和适合于多商家环境等实用性质，而且满足最强等级的不可分割性。此外，本文系统不要求用户执行任何的对运算，而且与Pirker等的移动支付框架相兼容。效率分析表明，本文系统在运算和通信耗费方面较已有系统具有明显优势。今后将进一步优化用户端（特别是TPM）的运算效率，考虑所设计的系统与下一代TPM 2.0标准的兼容问题等。

[1] CHANG C C, SUN C Y. A secure and efficient authentication scheme for e-coupon systems[J]. Wireless Personal Communications, 2014,77(4): 2981-2996.

[2] HSUEH S C, CHEN J M. Sharing secure m-coupons for peer-generated targeting via eWOM communications[J]. Electronic Commerce Research and Applications, 2010, 9(4): 283-293.

[3] CHEN L, ENZMANN M, SADEGHI A R, et al. A privacy-protecting coupon system[C]//The 9th International Conference on Financial Cryptography and Data Security. Roseau, 2005: 93-108.

[4] NGUYEN L. Privacy-protecting coupon system revisited[C]//The 10th International Conference on Financial Cryptography and Data Security.Anguilla, British West Indies, 2006: 266-280.

[5] CHEN L, ESCALANTE A, LÖHR H, et al. A privacy-protecting multi-coupon scheme with stronger protection against splitting[C]//The 11th International Conference on Financial Cryptography and Data Security. Scarborough, Trinidad and Tobago, 2008: 29-44.

[6] LÖHR H. Privacy-preserving protocols and applications for trusted platforms[D]. Bochum: Ruhr-Universit, 2012.

[7] 柳欣, 徐秋亮. 实用的强不可分割多重息票方案[J]. 计算机研究与发展, 2012,49(12): 2575-2590.LIU X, XU Q L. Practical multi-coupon systems with strong unsplittability[J]. Journal of Computer Research and Development, 2012,49(12): 2575-2590.

[8] 柳欣, 徐秋亮. 并发安全的紧凑多重息票方案[J].电子学报,2012,40(5): 877-882.LIU X, XU Q L. Compact multi-coupon systems with concurrent security[J]. Acta Electronica Sinica, 2012, 40(5):877-882.

[9] HINAREJOS M F, ISERN-DEYÀ A P, FERRER-GOMILA J L, et al.MC-2D: an efficient and scalable multicoupon scheme[J]. The Computer Journal, 2015, 58(4): 758-778.

[10] WANG W J, FENG D G, QIN Y, et al. ExBLACR: extending BLACR system[C]//The 19th Australasian Conference on Information Security and Privacy. Wollongong, NSW, Australia, 2014:397-412.

[11] XI L, FENG D G. FARB: fast anonymous reputation-based blacklisting without TTPs[C]//The 13th Workshop on Privacy in the Electronic Society. Scottsdale, Arizona, USA, 2014:139-148.

[12] CANARD S, GOUGET A, HUFSCHMITT E. A handy multi-coupon system[C]//The 4th International Conference Applied Cryptography and Network Security. Singapore, 2006: 66-81.

[13] ISERNS-DEYÀ A P, HUGUET-ROTGER L, PAYERAS-CAPELLÀ M M, et al. On the practicability of using group signatures on mobile devices: implementation and performance analysis on the android platform[J]. International Journal of Information Security, 2014,(8): 1-11.

[14] CHOW S S M, AU M H, SUSILO W. Server-aided signatures verification secure against collusion attack[J]. Information Security Technical Report, 2013, 17(3): 46-57.

[15] CANARD S, DEVIGNE J, SANDERS O. Delegating a pairing can be both secure and efficient[C]//The 12th International Conference on Applied Cryptography and Network Security. Lausanne, Switzerland,2014: 549-565.

[16] BRICKELL E, LI J T. A pairing-based DAA scheme further reducing TPM resources[C]//The 3rd International Conference on Trust and Trustworthy Computing. Berlin, Germany, 2010: 181-195.

[17] 杨波, 冯登国, 秦宇, 等. 基于可信移动平台的直接匿名证明方案研究[J]. 计算机研究与发展, 2014,51(7):1436-1445.YANG B, FENG D G, QIN Y, et al. Research on direct anonymous attestation scheme on trusted mobile platform[J]. Journal of Computer Research and Development, 2014, 51(7): 1436-1445.

[18] CESENA E, LÖHR H, RAMUNNO G, et al. Anonymous authentication with TLS and DAA[C]//The 3rd International Conference on Trust and Trustworthy Computing. Berlin, Germany, 2010: 47-62.

[19] CHEN L. A DAA scheme requiring less TPM resources[C]//The 5th International Conference on Information Security and Cryptology.Beijing, China, 2010: 350-365.

[20] 张倩颖, 冯登国, 赵世军. 基于可信芯片的平台身份证明方案研究[J]. 通信学报,2014,35(8):95-106.ZHANG Q Y, FENG D G, ZHAO S J. Research of platform identity attestation based on trusted chip[J]. Journal on Communications,2014,35(8):95-106.

[21] BALDIMTSI F, LYSYANSKAYA A. Anonymous credentials light[C]//2013 ACM SIGSAC conference on Computer amp; Communications Security. Berlin, Germany, 2013:1087-1098.

[22] PIRKER M, SLAMANIG D. A framework for privacy-preserving mobile payment on security enhanced arm trustzone platforms[C]//Proceedings in 2012 IEEE 11th International Conference on Trust,Security and Privacy in Computing and Communications. Liverpool,UK, 2012: 1155-1160.

[23] AU M H, SUSILO W, MU Y, et al. Constant-size dynamic k-times anonymous authentication[J]. IEEE Systems Journal, 2013, 7(2):249-261.

[24] YANG Y, DING X, LU H, et al. Self-blindable credential: towards lightweight anonymous entity authentication[EB/OL]. https://eprint.iacr.org/2013/207.pdf.

[25] PENG K, YI L. Studying a range proof technique-exception and optimization[C]//The 6th International Conference on Cryptology in Africa. Cairo, Egypt, 2013: 328-341.

[26] DODIS Y, YAMPOLSKIY A. A verifiable random function with short proofs and keys[C]//The 8th International Workshop on Theory and Practice in Public Key Cryptography. Les Diablerets, Switzerland,2005: 416-431

[27] SCOTT M. Unbalancing pairing-based key exchange protocols[EB/OL].https://eprint.iacr.org/2013/688.pdf.

[28] AU M H, SUSILO W, YIU S M. Event-oriented k-times revocable-iff-linked group signatures[C]//The 11th Australasian Conference on Information Security and Privacy. Melbourne, Australia, 2006:223-234.

[29] PENG K. A general, flexible and efficient proof of inclusion and exclusion[C]//Cryptographers’ Track at the RSA Conference 2011. San Francisco, CA, USA, 2011: 33-48.

[30] CAMENISCH J, LYSYANSKAYA A. A signature scheme with efficient protocols[C]//The 3rd International Conference on Security in Communication Networks. Amalfi, Italy, 2002: 268-289.

[31] PENG K, BOYD C, DAWSON E. Batch zero knowledge proof and verification and its applications[J]. ACM Transactions on Information and System Security, 2007, 10(2): 1-28.

Lightweight multi-coupon system for multi-merchant environments with DAA

LIU Xin1,2, XU Qiu-liang3, ZHANG Bo4
（1. School of Information Engineering, Shandong Youth University of Political Science, Jinan 250103, China;2. Key Laboratory of Information Security and Intelligent Control in Universities of Shandong(Shandong Youth University of Political Science), Jinan 250103, China;3. School of Computer Science and Technology, Shandong University, Jinan 250101, China;4. School of Information Science and Engineering, University of Jinan, Jinan 250022, China）

A multi-coupon system for multi-merchant environments was proposed by extending the DAA (direct anonymous attestation) scheme of Brickell etc. The new system bound the key elements in multi-coupon with the tamper-resistant TPM（trusted platform module）chip, so that it could prevent users from sharing behavior more effectively.By using the server-aided signature verification of Chow etc, the self-blindable credential technique of Yang etc, and range proof of Peng etc, the new system does not require customers to perform expensive pairing operations in the issue protocol and the redeem protocol. Compared with previous similar systems, the new system simultaneously satisfies several ideal properties and it is compatible with the mobile payment framework on the ARM TrustZone platform. Moreover,it has obvious advantages in aspects of communication and computation costs.

multi-coupon, direct anonymous attestation, server-aided signature verification, range proof, unsplittability

s: The National Natural Science Foundation of China(No. 61173139), Shandong Provincial Natural Science Foundation(No.ZR2015FL023, No.ZR2014FL011),The Project of Shandong Province Higher Educational Science and Technology Program(No.J14LN61), The Doctoral Research Start-up Funding Project of Shandong Youth University of Political Science (No.14A007)

TN918.2

A

10.11959/j.issn.1000-436x.2016175

2015-09-24；

2016-07-07

国家自然科学基金资助项目（No.61173139）；山东省自然科学基金资助项目（No.ZR2015FL023, No.ZR2014FL011）；山东省高等学校科技计划资助项目（No.J14LN61）；山东青年政治学院博士科研启动经费资助项目（No.14A007）

柳欣（1978-），男，山东广饶人，博士，山东青年政治学院副教授，主要研究方向为密码学与信息安全。

徐秋亮（1960-），男，山东淄博人，山东大学教授、博士生导师，主要研究方向为密码学与信息安全。

张波（1981-），男，山东德州人，博士，济南大学讲师，主要研究方向为密码学与信息安全。