基于区间证据理论的多传感器数据融合水质判断方法

周剑，马晨昊，刘林峰，孙力娟，肖甫

(1. 南京邮电大学计算机学院，江苏 南京 210023；2. 江苏省无线传感网高技术研究重点实验室，江苏 南京210023)

基于区间证据理论的多传感器数据融合水质判断方法

周剑1,2，马晨昊1,2，刘林峰1,2，孙力娟1,2，肖甫1,2

(1. 南京邮电大学计算机学院，江苏 南京 210023；2. 江苏省无线传感网高技术研究重点实验室，江苏 南京210023)

针对传感网测量水质数据过程中存在的必然不确定性和随机不确定性，提出了一种基于区间证据理论的多传感器数据融合水质判断方法。考虑传感器精度误差以及测量数据异常等问题，将每个传感器测量的水质数据用区间数表示，通过计算水质数据与每个水质等级特征值之间的距离，得到判断水质等级的区间证据。按照区间证据组合规则将多传感器的区间证据融合成综合区间证据，最后根据决策准则，由综合区间证据判断水质等级。实验表明，该方法能够从不确定水质数据中准确判断水质等级。

水质判断；区间证据理论；传感网；多传感器数据融合；不确定性

1 引言

水质监测是水污染防治的重要手段，传统的水质监测主要以人工现场采样、实验室仪器分析为主。但传统的水质监测存在监测频次低、采样误差大、监测数据分散、不能及时反映水污染变化状况等缺陷，难以满足政府和企业进行有效水环境管理的需求[1,2]。目前，水质自动监测已经成了连续获得水质数据的有效手段。其中，最常见的方法是通过部署多个传感器来组成无线传感网（WSN，wirelesssensor network）来收集水质数据。卞贺明等[3]设计了用于水质监测的传感器芯片并构建了相关系统，但没有涉及如何对水质进行判断。张珏[4]提出基于无线传感网的水质在线监测系统，该系统基于水质模型对水质进行预测，但并不能很好地判断当前水质状况。如何根据传感网测量的数据进行水质判断，是需要解决的问题。

无线传感网包括多个传感器，每个传感器负责测量一定区域的水质，由于传感器测量的数据众多，如何处理多传感器测量的众多数据是水质判断过程中的重点问题。在处理多传感器数据方面，数据融合是一种将不同来源数据加以处理、融合，从而得到一个更精确结果的重要技术。近几年，多传感器数据融合技术得到了广泛的关注，但更多应用是在目标识别[5]、隐私保护[6]、数据通信[7]等领域。本文将多传感器数据融合技术应用于水质判断。

一方面，传感器在测量水质数据的过程中，由于传感器精度问题，使测量的数据有一定误差；传感器测量的某些水质参数，如溶解氧会随温度、光照等因素而时刻发生变化，使测量的数据在一定范围内扰动。上述情况会造成传感网每次测量的数据具有不确定性，本文称这种不确定性为必然不确定性。区间数是在20世纪70年代中期，由4位学者分别独立地在模糊集合中提出。区间数能够表示不确定信息或不完整信息，适合表达信息缺乏、不确定性高的数据[8]。本文用区间数来表示传感器测量的带有必然不确定性的水质数据。

另一方面，传感器因自身老化可能会造成测量数据异常，其周围环境异常变化也可能对无线传感网的数据传输造成干扰，使传输的数据出现差错。上述情况无法预测，本文称这种无法预测的不确定性为随机不确定性。处理这种不确定性的常见方法有Dempster-Shafer证据理论（D-S证据理论）和贝叶斯方法。贝叶斯方法的基本策略是，事先确定先验概率和条件概率，则后验概率可以用贝叶斯公式进行估计，文献[9～11]将贝叶斯方法应用于多传感器数据融合，但是，只有在先验概率和条件概率充足且合适的时候才能够得到有效融合。在很多情况下，先验概率和条件概率不充足，D-S证据理论被认为是古典概率推理的扩展，能够在先验概率未知的情况下处理不确定性问题，得到较好的融合结果，因此，近年来，D-S证据理论引起了广泛的研究和关注[12]，文献[13～15]将D-S证据理论用于多传感器数据融合。

对于传感网测量的水质数据中存在的必然不确定性和随机不确定性，目前没有合适的相关方法能够同时处理，本文提出基于区间证据理论的多传感器数据融合水质判断方法。本文方法将传感器测量的数据用区间数表示，将每个传感器测量的数据作为判断水质等级的一个证据，通过区间证据理论进行多传感器数据融合，最后根据决策准则判断当前水质等级。

2 相关知识概述

2.1 区间数定义及基本运算

1) 区间数[16]：设 R表示实数集。对任意的，如果则称[c]为一个区间数。

当c−=c+时，区间数[c]即为普通实数；若 2个区间数[c]和[d]相等，则当且仅当c−=d−，c+=d+时，记作[c]=[d]。

2) 区间数基本运算[16]

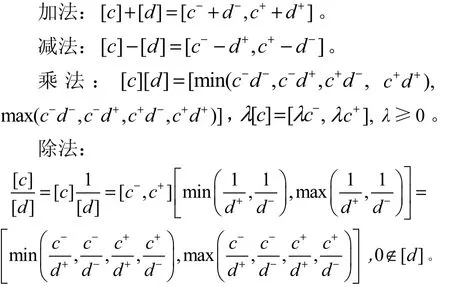
2.2 D-S证据理论概述

D-S证据理论是Dempster于1967年首先提出，由他的学生Shafer于1976年进一步发展起来的一种不精确推断理论，也称为Dempster-Shafer 证据理论，具有处理不确定信息的能力。D-S证据理论[18,19]描述如下。

1) 识别框架：设Θ为一个集合，称为识别框架。Θ中的元素相互排斥、有穷，通常表示所考察判断的事物或对象。识别框架Θ的子集构成了求解问题的各种解答，Θ子集所构成的集合称为Θ的幂集，记作Ω(Θ)。

2) 基本概率分配函数：也称mass函数，定义如下。

Dempster组合规则：设A⊆Θ，m1和m2是Θ上的2个mass函数，则

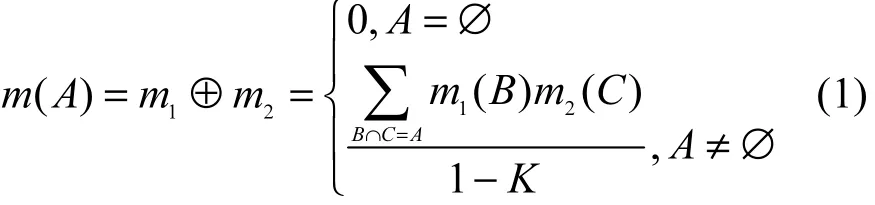
2.3 区间证据理论

在实际情况中，传感器测量的数据会因传感器老化、传输差错而具有随机不确定性。经典D-S证据理论在处理随机不确定性上得到广泛应用，但局限于单值数据。文献[20,21]提出了区间基本概率分配(IBPA，interval basic probability assignment)。该形式的证据能够较为全面地度量信息的不确定性，而且符合人的常性思维[21]。

在区间证据融合方面，Denoeux[20]构造二次规划模型以融合多个IBPA，给出了IBPA 有效性和归一化准则，提出了 Demspter 区间证据组合规则。基于Denoeux的研究，Wang等[21]提出了区间证据组合规则的求解方法。下面将对区间证据以及区间证据组合规则进行介绍。

令Θ为识别框架，A1, A2,⋅⋅⋅,An是n个Θ的子集，是n个区间数，

1) 区间基本概率分配

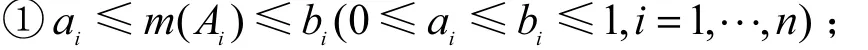
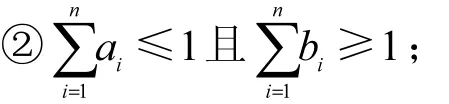
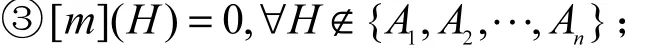
2) 归一化准则

有效的 IBPA并不一定是归一化的 IBPA，若IBPA未经归一化，则可用式(4)进行归一化处理。

对IBPA进行归一化处理，可以降低冗余、减小区间宽度[22]。

3) Dempster区间组合规则

若[m]1和[m]2是有效且归一化的IBPA，分别为和，融合结果标记为其区间值为

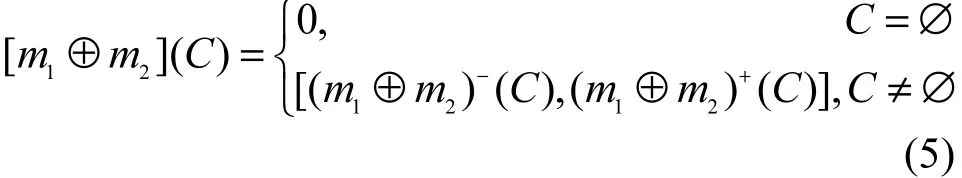
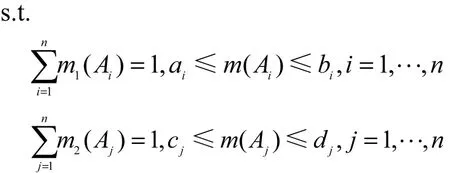
3 基于区间证据理论的多传感器数据融合水质判断

本文采用漂浮式传感器节点对水质进行测量，如图1所示。由于传感器节点相互独立，可以将每个传感器节点测量的水质数据作为证据理论中的证据。本文对测量的水质数据进行计算，得到每个等级水质的 IBPA，通过区间证据组合规则得到每个水质等级的综合信度分配，进一步按照决策准则得到水质等级判断结果。

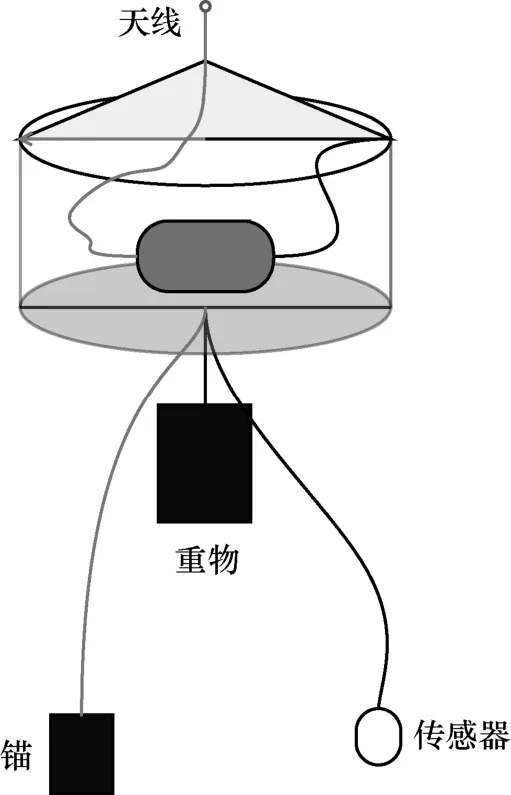
图1 漂浮式传感器

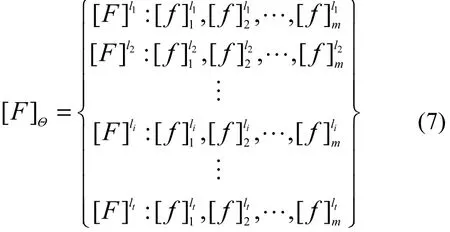
其中，[F]li表示水质等级为li的水质参数特征值，f表示溶解氧、氨氮、总氮、总磷等水质参数，m表示参数个数。每个特征值均为区间数。

在证据理论中，mass函数表示分配的信度。本文中 mass函数表示水质判断为不同等级的区间信度。表示用传感器k测量的水质数据计算得到的mass分配，其中，表示对其测量水域水质等级判断为lt的区间信度，其值根据[S]k与lt等级水质参数特征值的距离计算得到。

由于传感器测量的数据具有不确定性，为了能更准确地判断水质等级，在区间证据组合之前，用可靠性系数C对mass函数进行修正。通过区间证据组合规则综合修正后的 mass分配，得到综合区间证据，最后按照决策准则判断水质等级。基于区间证据理论的多传感器数据融合水质判断过程如图2所示。

3.1 基于区间水质数据的mass函数

在本文方法中，首要问题是如何将传感器测量的原始数据转化为区间证据，因此，需要对原始数据进行处理，构建mass函数。

图2 基于区间证据理论的多传感器数据融合水质判断过程

显然，[S]k与[F]li相差越小，当前水质等级为li的可能性越大；[S]k与[F]li相差越大，当前水质等级为li的可能性越小。本文基于区间闵可夫斯基公式[23]计算[S]k与[F]li的距离

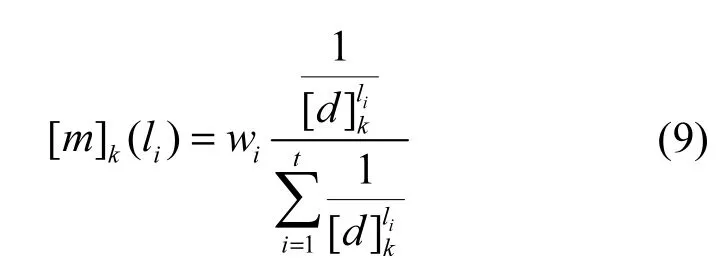
3.2 可靠性系数

传感器测量数据带有不确定性，为了能更准确地判断水质等级，通过可靠性系数对mass函数进行修正。传感器k的可靠性系数如式(10)所示。

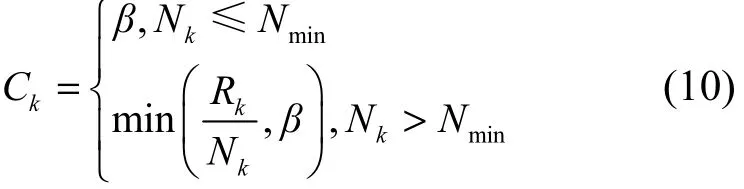
其中，Nk表示传感器k进行水质判断的总次数，Rk表示传感器k进行水质判断正确的次数，β和Nmin为固定值，如果水质判断的总次数小于等于Nmin，则使用β作为可靠性系数。

如果传感器可靠性较高，该传感器区间证据对应的可靠性系数较大，该区间证据在区间证据组合过程中对组合结果的影响较大；如果传感器可靠性较低，该传感器区间证据对应的可靠性系数较小，该区间证据在区间证据组合过程中对组合结果的影响较小。

经过可靠性系数修正后的mass函数为

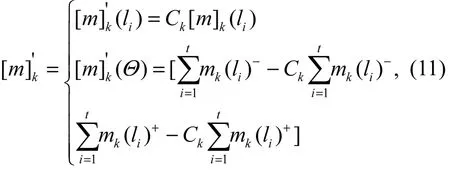
3.3 水质等级判断

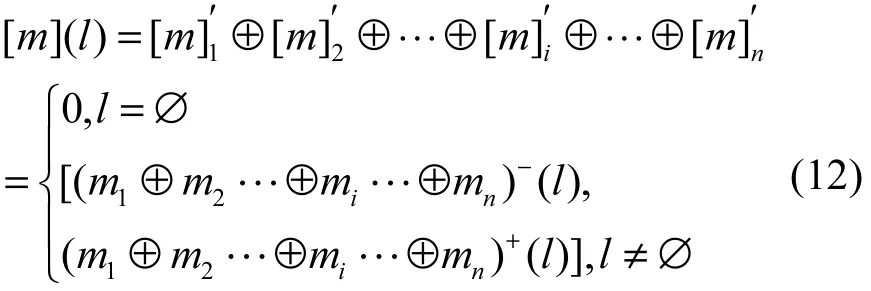
通过该组合规则可以将多个传感器的区间证据组合为(0,1)区间内的综合区间证据，以表达对不同水质等级的综合区间信度分配。得到每个水质等级的综合区间信度后，按照以下决策准则判断水质等级。

1) 最大区间信度对应的水质等级即为当前水质等级。

2) 最大区间信度的中点值应当比其他等级的区间信度中点值至少大ρ，否则该水质等级信度与其他等级信度过于接近，水质等级不确定。

3) 分配给Θ的区间信度应当满足中点值不大于阈值γ，否则不确定度过大，水质等级不确定。

4 实验和结果

实验中，本文使用自己开发的传感器节点进行组网，对溶解氧（DO）、氨氮（NH3-N）、总磷（TP）、总氮（TN）等水质参数进行测量。设传感器测量精度分别为pTN=0.5。根据《国家地表水环境质量标准（GB3838-2002）》将水质分为5个等级，每一等级的水质参数特征值如表1所示。

1) 实验1

采用3个传感器节点S1、S2和S3，对一片水域水质进行监测，表2为3个传感器测得的水质数据。

从表1和表2中可以看出，传感器S1、S3测量的水质数据接近水质等级Ⅲ，传感器S2受到传感器精度影响，导致测量的水质数据介于水质等级Ⅱ和Ⅲ之间。

表1 水质参数特征值

表2 传感器S1、S2和S3测得的水质数据

根据式(8)，可以得到传感器 S1的测量数据与每个水质等级的水质参数特征值之间的距离D1。

通过式(9)，可以得到传感器 S1的每个水质等级mass函数值为：M1={[0.084 1,0.121 9], [0.130 4,0.228 8], [0.324 9, 0.472 6], [0.093 4,0.207 0], [0.048 0,0.099 4]}。类似地，可以得到传感器S2和 S3的各mass函数值，如表3所示。

设传感器S1、S2和S3进行水质判断的总次数都为50，传感器S1、S2和S3判断正确的次数分别为43、42、40，因此可靠性系数分别为0.86、0.84、0.80。

将表3的各mass函数值按照式(11)进行修正，结果如表4所示。

从表4中可以看出，传感器S1、S3支持水质等级为Ⅲ；传感器 S2对水质等级为Ⅱ和Ⅲ的信度十分接近。将S1和S2的区间证据，按照式(13)进行组合，结果如表5所示。

表3 传感器S1、S2和S3的各mass函数值

表4 传感器S1、S2和S3修正后的各mass函数值

表5 S1、S2和S3区间证据组合结果

从表5可以看出，传感器S1和S2的综合区间证据对水质等级Ⅲ分配的信度最大，但为0.040 5，大于阈值γ，不确定度过高，按照决策准则，无法进行判断。将传感器S1、S2和S3的区间证据进行组合，结果同样如表5所示。水质等级为Ⅲ的信度增大到[0.250 7, 0.711 5]，降低到0.019 8，小于阈值γ。按照决策准则，可以判断当前水质等级为Ⅲ。从本实验可以看出，本文提出的方法能够从带有必然不确定性的水质数据中，得出准确的水质等级判断结果。

2) 实验2

在实验1的基础上，有另外2个传感器节点S4和S5。测得的水质数据如表6所示。从表6中可以看出，传感器 S4测得的水质数据不同于其他传感器，该传感器测量数据可能出现差错。

通过式(11)计算出传感器S4和S5的每个水质等级mass函数值，如表7所示。

传感器S4和S5的可靠性系数分别为0.8和0.9，将表7中的各mass函数值按照式(11)进行修正，结果如表8所示。

从表8可以看出，传感器S4给出了不同结论。按照式(13)，将传感器S1、S2、S3、S4的区间证据进行组合，结果如表9所示。可以看到，水质等级为Ⅲ的区间信度最大，其值为[0.152 9,0.742 9]。然而，按照决策准则，无法进行判断。将传感器S1、S2、S3、S4、S5的区间证据进行组合，结果同样如表9所示。可以看到，水质等级为Ⅲ的信度增大到[0.199 1,为0.541 05。根据决策准则，判断水质等级为Ⅲ类。从本文实验中可以看出，所提方法能够从带有随机不确定性的水质数据中，得出准确的水质等级判断结果。

3) 实验3

在水质判断方法中，单因子水质标识指数法[24]是比较常用的水质判断方法。将本文方法与单因子水质标识指数法进行对比。通过计算机仿真 10个传感器节点，分别在传感器错误率为40%、35%、30%、25%、20%的情况下，对一片已知水质等级的水域进行水质测量。每种错误率下仿真出 20组水质数据，同组数据分别采用本文方法与单因子水质标识指数法进行水质判断，结果如表10所示。

表6 传感器S4和S5测得的水质数据

表7 传感器S4和S5的各mass函数值

表8 传感器S4和S5修正后的各mass函数值

表9 S1、S2、S3、S4、S5区间信度组合结果

从表 10中可以看出，在不同的传感器错误率情况下，本文方法得到的水质判断正确率均要高于单因子水质标识指数法。采用单因子水质标识指数法，水质判断错误率会随着传感器错误率的提高而提高。本文方法可以减小传感器发生错误对水质判断造成的影响，避免水质等级判断错误，因此，本文方法要优于单因子水质标识指数法。由于水质数据的不确定性，本文方法会产生水质等级不确定的判断，可以使用人工进一步分析，以得到更准确的水质判断结果。

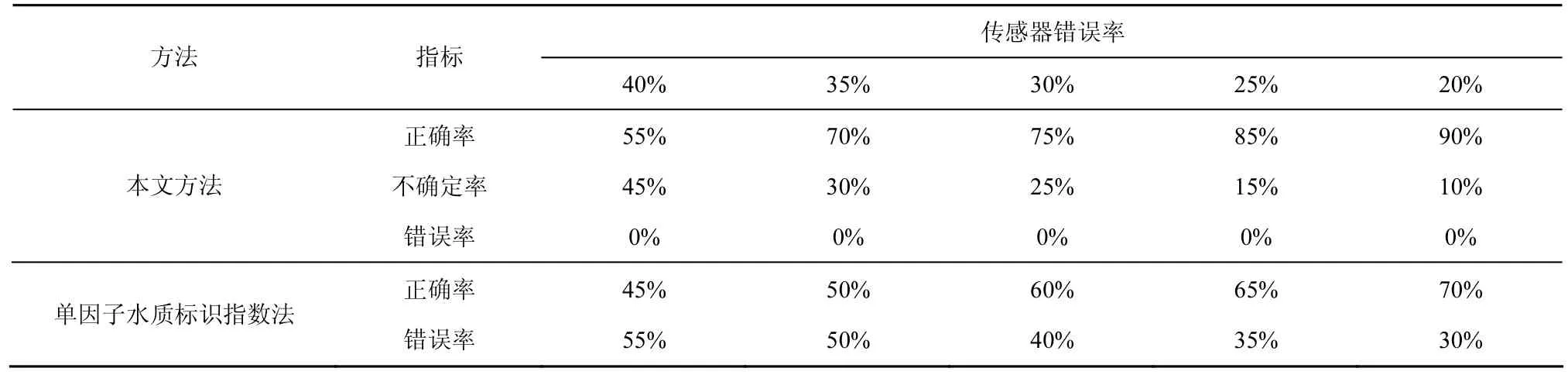
表10 本文方法与单因子水质标识指数法对比

5 结束语

本文将多传感器数据融合技术应用于水质判断。针对传感网测量水质数据过程中存在必然不确定性和随机不确定性，提出了一种基于区间证据理论的多传感器数据融合水质判断方法。在本文方法中，将每个传感器测量的水质数据用区间数表示，并将其作为判断水质等级的一个证据。将测得的水质数据与水质等级特征值计算距离，利用该距离构造mass函数。用可靠性系数对mass函数进行修正，按照区间证据组合规则对各传感器的区间证据进行融合，得到每个水质等级的综合区间证据。按照决策准则，判断当前水质等级。实验表明，本文方法能够减小传感器精度误差对水质判断造成的影响，能够在个别传感器数据异常的情况下，准确判断出水质等级。

[1] ZHOU J, LIU L F, GUO J, et al. Multisensor data fusion for water quality evaluation using Dempster-Shafer evidence theory[J]. International Journal of Distributed Sensor Networks, 2013, (2):1-6.

[2] HALL J, SZABO J. Water sentinel online water quality monitoring as an indicator of drinking water contamination[R]. New York:Environmental Protection Agency, 2005.

[3] 卞贺明, 边超, 佟建华, 等. 用于氨氮检测的三维微纳氨气传感芯片及系统研究[J]. 电子与信息学报,2012,34(5): 1258-1262.BIAN H M, BIAN C, TONG J H, et al. Miniaturized 3D micro/nano ammonia sensor chip and system for measurement of ammonia nitrogen[J]. Journal of Electronics amp; Information Technology, 2012,34(5): 1258-1262.

[4] 张珏. 基于无线传感器网络的水质在线监测系统研究[D]. 重庆:重庆大学, 2010.ZHANG J.Research on water quality online monitoring system based on wireless sensor network[D]. Chongqing: Chongqing University,2010.

[5] 闫光. 基于多传感器信息融合的动态目标检测与识别[D]. 北京:北京理工大学, 2015.YAN G. Moving target detection and recognition based on multi-sensor information fusion[D]. Beijing: Beijing Institute of Technology, 2015.

[6] 赵小敏, 梁学利, 蒋双双, 等. 安全的 WSN 数据融合隐私保护方案设计[J]. 通信学报, 2014, 35(11): 154-161.ZHAO X M, LIANG X L, JIANG S S, et al.Design of secure privacy-preserving data aggregation scheme for wireless sensor network[J]. Journal on Communications, 2014, 35(11): 154-161.

[7] 乐俊, 张维明, 肖卫东, 等. 无结构动态适应无线传感器网络数据融合算法[J]. 通信学报, 2012,33(9): 53-65.YUE J, ZHANG W M, XIAO W D, et al.Structure-free and dynamicadaptive data fusion algorithm for wireless sensor networks[J]. Journal on Communications, 2012, 33(9):53-65.

[8] 康兵义, 李娅, 邓勇, 等. 基于区间数的基本概率指派生成方法及应用[J]. 电子学报, 2012, 40(6): 1902-1906.KANG B Y, LI Y, DENG Y, et al. Determination of basic probability assignment basedon interval numbers and its application[J]. Acta Electronica Sinica, 2012, 40(6): 1902-1906.

[9] BREHARD T, KRISHNAMURTHY V. Optimal data incest removalin Bayesian decentralized estimation over a sensor network[C]//The IEEE International Conference on Acoustics,Speech and Signal Processing. 2007: 173-176.

[10] WILSON D H, ATKESON C.Simultaneous tracking andactivity recognition (STAR) using many anonymous, binarysensors[C]//The 3rd International Conference onPervasive Computing. 2005: 62-79.

[11] MASKELL S. A Bayesian approach to fusing uncertain,impreciseand conflicting information[J]. Information Fusion, 2008,9(2): 259-277.

[12] 于美婷, 赵林靖, 李钊.基于 DS证据理论的协作频谱感知改进方法[J]. 通信学报, 2014, 35(3): 168-173.YU M T, ZHAO L J, LI Z. Improved cooperative spectrum sensing scheme based ondempster-shafer theory in cognitive radio network[J].Journal on Communications, 2014,35(3):168-173.

[13] BASIR O, YUAN X. Engine fault diagnosis based on multisensory information fusion using dempster-shafer evidencetheory[J]. Information Fusion, 2007,8(4): 379-386.

[14] ZHU D, GU W. Sensor fusion in integrated circuit faultdiagnosis using a belief function model[J]. International Journalof Distributed Sensor Networks, 2008,4(3):247-261.

[15] LI J M, LUO S H, JIN J S. Sensor data fusion for accuratecloud presence prediction using Dempster-Shafer evidencetheory[J].Sensors,2010,10(10): 9384-9396.

[16] ALEFELDA G, MAYERB G. Interval analysis: theory and applications[J]. Journal of Computational and Applied Mathematics,1999, 121(1/2): 421-464.

[17] 曾文艺, 罗成忠, 肉孜阿吉. 区间数的综合决策模型[J].系统工程理论与实践,1997,17(11): 48-50.ZENG W Y, LUO C Z, ROZI H. Comprehensive decision model ofiInterval-number[J]. System Engineering Theory and Practice,1997,17(11): 48-50.

[18] DEMPSTER A P. Upper and lower probabilities induced by amultiple valued mapping[J]. The Annals of Mathematical Statistics, 1967, 38(2):325-339.

[19] SHAFER G A. Mathematical theory of evidence[M]. Princeton:Princeton University Press, 1976.

[20] DENOEUX T. Modelling vague belief using fuzzy-valued beliefstructures[J]. Fuzzy Sets and Systems, 2000, 116(2): 167-199.

[21] WANGY M, YANGJ B,XU D L, et al. The evidential reasoning approach for multiple attribute decision analysis using interval belief degrees[J].European Journal of Operational Research, 2006, 175(1): 35-66.

[22] 冯海山, 徐晓滨, 文成林.基于证据相似性度量的冲突性区间证据融合方法[J]. 电子与信息学报, 2012, 34(4): 851-857.FENG H S, XU X B,WEN C L. A new fusion method of conflicting interval evidencebased on the similarity measure of evidence[J]. Journal of Electronics amp; Information Technology, 2012, 34(4): 851-857.

[23] 曾文艺,赵宜宾.基于区间数度量的区间值模糊集合的归一化距离、相似度、模糊度和包含度的关系研究[J]. 模糊系统与数学, 2012,26(2):81-90.ZENG W Y,ZHAO Y B. Relationship among the normalized distance,the similarity measure,the entropy and the inclusion measure of interval-valued fuzzy setsbased on interval-number measurement[J].Fuzzy Systems and Mathematics, 2012, 26(2): 81-90.

[24] 徐祖信.我国河流单因子水质标识指数评价方法研究[J]. 同济大学学报(自然科学版), 2005,33(3): 321-325.XU Z X. Single factor water quality ident ification index for environmentalquality assessment of surface water[J]. Journal of Tongji University (Natural Science), 2005, 33(3): 321-325.

Multi-sensor data fusion method for water quality evaluation based on interval evidence theory

ZHOU Jian1,2, MA Chen-hao1,2, LIU Lin-feng1,2, SUN Li-juan1,2, XIAO Fu1,2
(1. College of Computer, Nanjing University of Posts and Telecommunications, Nanjing 210023, China;2. Jiangsu High Technology Research Key Laboratory for Wireless Sensor Networks, Nanjing 210023, China)

For the inevitable uncertainty and random uncertainty in the process of measuring water quality data with the sensor network, a multi-sensor data fusion method for water quality evaluation based on interval evidence theory was proposed. Considering the precision error of sensor and the abnormalities of measured data, every water quality data measured by sensor was represented by interval number. By calculating the distance between the water quality data and the features of each water quality class, the interval evidence of water quality class was acquired. According to the interval evidence combining rule, a comprehensive interval evidence was obtained by combining the interval evidence of each sensor. Finally, the water quality class was determined based on the comprehensive interval evidence by the decision rule. Experiments show that the proposed method can evaluate water quality class more accurately from the uncertain water quality data.

water quality evaluation, interval evidence theory, sensor network, multi-sensor data fusion, uncertainty

s: The National Natural Science Foundation of China (No.71301081, No.61373139, No.61572261, No.61300165,No.61302157), The Natural Science Foundation of Jiangsu Province (No.BK20130877, No.BK20140895), Postdoctoral Science Foundation of China (No.2014M551637), Postdoctoral Science Foundation of Jiangsu Province (No.1401046C), The Scientific Research Foundation of Nanjing University of Posts and Telecommunications (No.NY213035)

TP393

A

10.11959/j.issn.1000-436x.2016174

2016-05-29；

2016-09-06

刘林峰，liulf@njupt.edu.cn

国家自然科学基金资助项目（No.71301081, No.61373139, No.61572261, No.61300165, No.61302157）；江苏省自然科学基金资助项目（No.BK20130877, No.BK20140895）；国家博士后基金资助项目（No.2014M551637）；江苏省博士后基金资助项目（No.1401046C）；南京邮电大学引进人才基金资助项目（No.NY213035）

周剑（1984-），男，江苏扬州人，南京邮电大学副教授，主要研究方向为传感器网络、数据融合。

马晨昊（1990-），男，河南新乡人，南京邮电大学硕士生，主要研究方向为数据融合。

刘林峰（1981-），男，江苏丹阳人，南京邮电大学副教授，主要研究方向为传感器网络。

孙力娟（1963-），女，江苏南京人，南京邮电大学教授，主要研究方向为传感器网络。

肖甫（1980-），男，湖南邵阳人，南京邮电大学教授，主要研究方向为传感器网络。